泸定大渡河桥重力锚碇基础形式研究
周霆,陶齐宇,李则均
(四川省公路规划勘察设计研究院有限公司,四川 成都 610041)
0 引言
锚碇作为将悬索桥主缆拉力传递给地基的关键构件,其结构形式选用应根据地质、地形、水文及主缆力等建设条件来确定。重力锚通过自身重力和地基摩擦力承担主缆缆力,传力机理简单,对地质条件适应性较强,因而无论山区还是沿海地区,都得到了广泛的应用。重力锚抗倾覆和抗滑移的稳定性一直是设计的关键问题,与锚碇基础形式和持力层土体力学性能密切相关[1-3]。邵国建等[4-5]对软土深厚覆盖层锚碇基础形式进行研究,陈维等[6]通过考虑夹持效应,对基岩上的重力锚基础形式进行优化。
西部地区建设的悬索桥,桥位多基岩出露,覆盖层较浅,重力锚一般以岩石作为基础持力层,如南溪长江大桥、坝陵河大桥等。受第四纪冰期影响,冰碛土在中国西部广泛分布,在冰碛土上建设重力锚还没有相关实践,本文以泸定大渡河桥为依托,从锚碇稳定性入手,研究冰碛土上修建重力锚碇的合理基础形式,为类似工程提供借鉴。
1 工程概况
泸定大渡河桥位于泸定县泸桥镇咱里村,下距著名的红军铁索桥约5.2 km,是雅安至康定高速公路的控制性工程和标志性建筑。
大桥主桥为1 100 m 单跨悬索桥[7],主梁采用钢桁梁,雅安岸采用隧道锚,康定岸采用重力锚;两岸桥塔均采用门形钢筋混凝土塔,引桥采用34 m(30 m)跨连续箱梁桥;大桥全长1 411.0 m。桥型布置如图1 所示。

图1 泸定大渡河桥总体布置图(单位:m)Figure 1 General layout of Dadu River bridge in Luding (unit:m)
2 重力锚地形地质条件
重力锚处为一山包,台地横向宽约300 m,纵向长约500 m,高差为150 m,为山脊向前突出缓坡平台,岸坡稳定。
山包上部为第四系上更新统冰碛层的冰碛土,最大厚度187.1 m,以胶结较好的碎石土为主,夹少量角砾和黏土(图2),碎石成分主要为闪长岩,局部夹少量花岗岩,巨粒、粗粒含量高于50%,土体干燥,密实,部分半胶结、力学性质好(图3),天然含水率约43%,由于土体密实度较高,土体的渗透性较差,通过钻孔注水试验测试,渗透系数为0.01~0.1 m/d。冰碛层下为古元界闪长岩,岩体风化层浅,岩体完整性较好,为冰碛土提供了天然的抗滑稳定保障。

图2 冰碛土典型钻芯照片Figure 2 Photo of typical cores of moraine soils

图3 现场剪切试验曲线Figure 3 Field shear test curve
3 锚体各部的设计
重力锚大致可分为基础、锚块、锚室、散索鞍支墩4 部分,后三项合并称作锚体。锚块主要承受锚固系统传递的主缆索股拉力,散索鞍支墩主要承受由散索鞍传递的主缆压力,锚室为封闭空间,对主缆索股起保护作用;基础、锚室、散索鞍支墩及锚块形成一个完整的三杆件人字状构造的空间受力构件。
重力锚的基础形式是重力锚设计的关键内容。通常是根据施工场地、地形和地质条件等综合因素来决定其结构形式,可分为直接基础和人工基础。直接基础是将锚体直接作用于持力层。人工基础是采用人工开挖工作,将基础作用到持力岩层或土层上。目前国内外常用的重力锚人工基础形式有扩大基础、群桩基础、沉箱(井)基础、地下连续墙基础和复合基础等形式。扩大基础设计简单、施工方便、造价节约,是基岩埋深较浅、地形地质条件良好的陆地或浅水区的首选形式。勘探试验表明:锚碇所处位置的冰碛土,其分布范围广、厚度大、地面3 m 以下土体密实、含水率低,虽然为非岩石类地基,但其力学性能良好,选择采用扩大基础形式。
4 扩大基础选型研究
悬索桥重力锚的整体验算包括地基应力验算、整体抗滑移验算、整体抗倾覆验算等。扩大基础的形式和尺寸对整体计算起控制作用,关系到基础方案的合理性,设计上对两种基础形式进行了比选。
为保证两方案的可比性,两种锚碇的总混凝土方量相同。方案1 为常用的支墩基础与锚块基础同平面的平底基础形式,构造如图4 所示,基底尺寸89.7 m×60 m(纵桥向×横桥向)。散索鞍支墩高34 m,支墩基础高10.2 m,锚块下基础高15.2 m;方案2为支墩基础与锚块基础不共面,采用带齿坎的鞍部将二者连接起来的斜向基础形式,构造如图5 所示,支墩基础部分尺寸41 m×60 m(纵桥向×横桥向),锚块基础部分尺寸40.7 m×60 m(纵桥向×横桥向),散索鞍高18.3 m,支墩基础高7 m,锚块基础高21 m。斜向鞍部设置3.3 m×3 m 抗滑齿坎。主缆成桥拉力为551 292 kN,入射角23.097°,主缆中心索股锚固角为40°,散索鞍支墩倾角58°,锚体总重2 391 946 kN。

图4 方案1:平底基础锚碇Figure 4 Scheme 1: Flat foundation anchorage
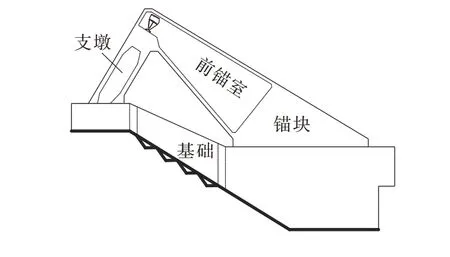
图5 方案2:斜向基础锚碇Figure 5 Scheme 2: Slant foundation anchorage
根据《公路悬索桥设计规范》(JTG/T D65-05—2015),锚碇的抗倾覆和抗滑动稳定性系数应大于2.0;锚碇基底最大应力值应满足地基承载容许值。
4.1 基底应力验算
地基应力按照《公路桥涵地基与基础设计规范》(JTG 3363—2019)第5.2 条进行计算。计算简图如图6、7 所示。

图6 方案1:平底基础Figure 6 Scheme 1:Flat foundation

图7 方案2:斜向基础Figure 7 Scheme 2:Slant foundation
分别求出方案1、2 基底应力如图8 所示。

图8 锚碇基底应力分布图Figure 8 Stress distribution diagram of anchorage foundation at base bottom
由图8 可知:两种基础形式的基底土应力均小于地基承载力800 kPa,方案1 水平基础锚碇由于外力对基底中心的合力矩为逆时针方向,因此计算得出的基底应力呈现前端大、后端小的变化趋势。而方案2 斜向基础锚碇由于外力对基底中心的合力矩为顺时针方向,因此计算得出的基底应力呈现前端小、后端大的变化趋势。
4.2 抗倾覆稳定验算
按照《公路桥涵地基与基础设计规范》(JTG 3363—2019) 第5.4.1 条计算抗倾覆稳定性。同时采用挡土墙抗倾覆验算公式,两种方法相互校核。
验算结果如表1 所示。

表1 抗倾覆稳定性系数Table 1 Anti-overturning stability coefficient
验算结果表明:无论采用何种算法,两种基础形式的锚碇抗倾覆稳定性均满足规范要求。但是方案2,整体重心比方案1 更靠后,稳定力矩更大;且采用倾斜基底后,主缆水平力的倾覆力臂,无论按算法1 取到基底重心的高度,还是按算法2 取到基础前趾点的高度,均小于方案1,因此倾覆弯矩减小,整体合力矩为顺时针方向。方案2 的稳定系数比方案1 提高38%。前面基底应力的验算结果,也间接验证了斜向基础锚碇的抗倾覆稳定性相比平底基础锚碇更优。
4.3 抗滑移稳定验算
锚碇基础底面的滑动抵抗力通常由以下几部分组成[8]:
(1) 基础底面和地基间的黏结力,为基础底面和地基间的黏结强度与有效承载面积的乘积。对于平基础与土或岩石的地基之间,通常不考虑该部分力。
(2) 基础底面和地基间的滑动摩阻力,为有效垂直荷载扣除主缆拉力的垂直分力和浮力后与摩阻系数的乘积。摩阻系数按规范取值或根据土工试验条件而定。
(3) 基础前部岩、土抗力,通常只在良好的嵌固和周边环境情况下才予以考虑,一般作为安全储备。
(4) 设置齿坎的基础,基础夹持的土体或岩石的剪切力,为夹持土体或岩体面积与土体或岩体的抗剪强度的乘积。抗剪强度主要与剪切滑动面黏聚力、基础与土体间摩擦角相关,可由现场试验确定。
对于方案1,抗滑力由基底与地基土之间的滑动摩阻力提供,如图9 所示。
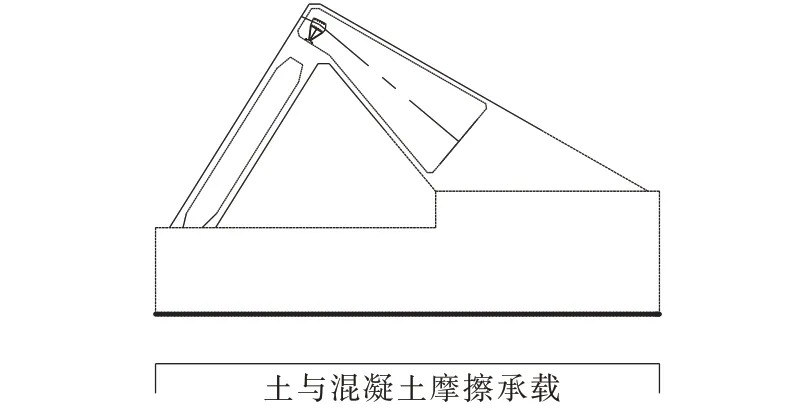
图9 平底基础锚碇基底摩擦力示意Figure 9 Friction force of flat foundation anchorage at base bottom
按照《公路桥涵地基与基础设计规范》(JTG 3363—2019)计算抗滑移稳定性:
式中:kc为抗滑动稳定性系数;∑Pi为竖向力总和;∑HiP为抗滑稳定水平力总和;∑Hia为滑动水平力总和;μ为基础底面与地基土之间的摩擦系数,根据地勘报告取μ=0.48。
对于方案2,抗滑力由锚块基底与地基土之间的摩擦力加上鞍部基底的齿坎作用抗力(即图10 中虚线抗滑面的齿坎效应)提供。

图10 斜向基础锚碇基底摩擦力示意Figure 10 Friction force of slant foundation anchorage at base bottom
齿坎效应所提供的抗滑力计算根据文献[9]提出的剪摩公式(考虑土体滑面剪切力)计算:
式中:Pmax为抗滑力的极限值;c0为滑动面上的黏聚力;A为基底面积;f为基底摩擦系数,f=tanφ0(φ0为基底与土质之间的摩擦角);Y和X分别为基础所受垂直方向与水平方向的力,Y根据前面基底应力计算结果取值,X为主缆力水平分力。
则抗滑移系数如式(3)所示,公式分子的前两项为斜向基础鞍部考虑齿坎效应的抗滑力,后一项为后锚块基底与土体间的摩擦力。
式中:c0A+fY1为夹持土体的夹持效应可产生的最大抗滑力;c0为土体黏聚力,取26 kPa;φ0取34°[7];土体与基底间摩擦系数μ取值0.48;A1为夹持部分土体的剪切面积,A1=43.66×60=2 619.6 m2;夹持部分基底反力Y1=1 037 258 kN,后锚块基底反力Y2=1 201 618 kN。X为主缆水平分力507 101 kN。
由上可见,齿坎作用对于锚碇的抗滑移稳定性有较好的改善作用,相比于平底基础锚碇,稳定系数提高29%,由于两个方案锚碇的混凝土方量相同,经测算,若要平底基础锚碇达到同样的抗滑移系数,则需增加混凝土24 000 m3。由此可见,锚碇采用带齿坎的斜向基础更为经济合理。
5 锚碇有限元数值模拟计算
为配合验证以上计算分析结论,分别对两种基础形式进行有限元数值模拟分析。分析软件采用Midas GTS NX,冰碛土体和锚碇结构均采用3D 实体单元。冰碛土采用莫尔-库仑模型,锚碇结构采用弹性模型,土体与锚碇结构之间的接触面采用莫尔-库仑模型。根据地勘试验报告成果,相关物理力学参数如表2 所示。土体边缘面采用固结约束,模型简图如图11、12 所示。

表2 模型物理力学参数Table 2 Physics and mechanics parameters of the model

图11 平底基础锚碇有限元模型图Figure 11 FE model of flat foundation anchorage

图12 斜向基础锚碇有限元模型图Figure 12 FE model of slant foundation anchorage
5.1 基底应力结果
两种基础形式的基底应力计算结果如图13、14所示。

图13 平底基础竖向土体应力(单位:kPa)Figure 13 Soil vertical stress of flat foundation anchorage(unit:kPa)

图14 斜向基础竖向土体应力(单位:kPa)Figure 14 Soil vertical stress of slant foundation anchorage(unit:kPa)
由图13、14 可以看出:斜向基础锚块基底平均应力400 kPa,支墩基底平均应力257 kPa,平底基础锚块基底平均应力256 kPa,支墩基底平均应力382 kPa,基底的应力分布趋势与理论分析一致。分析有限元结果与理论计算值存在些许偏差的主要原因为:① 理论计算将土体作为刚体计算,而实际上土体为弹性体,存在弹性变形,因此有限元分析结果小于理论计算结果;② 除了底面土体外,有限元模型还考虑了锚碇与侧面土体的相互作用,分担了基底受力。因此从工程角度来看,采用理论计算的结果是偏安全的。
5.2 斜向基础锚碇抗滑移有限元分析
在斜向基础锚碇模型中逐级增大主缆拉力,观察每个主缆拉力加载下对应基底土应力。当主缆力达到设计值的2.6 倍时,此时地基土最大竖向应力为292 kPa(图15)。根据土体剪力公式,求得当竖向应力为252 kPa 时,对应土的抗剪强度为:

图15 土体竖向应力(单位:kPa)Figure 15 Soil vertical stress(unit:kPa)
此时地基土允许的剪切应力值为196 kPa,查得最大竖向应力对应位置的剪切应力为197 kPa(图16),由此判断地基土此时处于即将破坏的临界状态。可推断出斜向基础锚碇的抗滑移系数为2.6,此值与前面理论计算值2.65 非常接近。这也初步验证了理论计算公式的适用性。

图16 土体剪切应力(单位:kPa)Figure 16 Soil shear stress(unit:kPa)
6 结论和展望
(1) 冰碛土广泛分布于西部山区,其力学性能良好。可因地制宜地将稳定性好、体量宽厚的土体,作为悬索桥重力锚碇基础的地基持力层,基础采用斜向扩大基础形式,可以有效减小锚碇的工程量,节省造价。
(2) 通过基础形式对锚碇抗倾覆稳定性影响的对比研究发现:采用斜向基础的锚碇由于整体重心作用点更靠后,稳定弯矩增加,且基底的斜向布置也有效减小了主缆的水平分力距离重心轴的竖向距离,从而减小了倾覆弯矩,因此比平底基础锚碇具有更好的抗倾覆稳定性。以本桥为例,在相同混凝土方量前提下,斜向基础比平底基础抗倾覆稳定系数提高38%。
(3) 通过基础形式对锚碇抗滑移稳定性影响的对比研究发现:采用斜向基础的锚碇,通过设置齿坎,利用齿坎效应参与抗滑移,相比平底基础,可有效提高锚碇的抗滑移能力。以本桥为例,在相同混凝土方量前提下,抗滑移系数比平底基础锚碇提高29%。
泸定大渡河桥2014 年动工,2018 年12 月31 日建成通车。在施工和运营期间均全程对重力锚碇跟踪监测,监测结果表明结构状态良好。鉴于其优秀的稳定性和经济性,带齿坎的斜向扩大基础重力锚构造形式,可以在类似工程建设条件下运用推广。

