不同截面选型对波纹钢箱涵受力性能影响分析

张顺，刘保东，高猛，武飞， 王志宏

（1.北京交通大学 土木建筑工程学院，北京市 100089；2.山东省交通规划设计院集团有限公司，山东 济南 250000；3.衡水益通管业股份有限公司，河北 衡水 053000）

0 引言

波纹钢板桥涵结构作为一种典型的柔性结构，具有较强的变形适应能力。相比于传统的混凝土圬工桥涵，具有自重小、施工速度快、使用周期长、对基础要求低等优点［1］，因此广泛应用于公路铁路桥涵和城市综合管廊中［2］。通过对国内外的研究和应用调研，波纹钢桥涵结构中有一种特殊的结构形式——波纹钢箱形结构［3］，相比于传统波纹钢管涵形式，其跨度更大，截面利用率更高，填土高度更小，更适合于路基高度受限的情况。覆土波纹钢箱涵结构通过土-结相互作用［4-5］，使土体和结构能够共同受力，保证土体和结构物的整体性。土体一方面作为荷载作用在波纹钢板上引起结构物变形；另一方面又作为承载体系的一部分，将结构上部荷载分散到两侧的土体上，大大提高结构物的承载和变形能力。

目前中国对波纹钢箱涵研究较少，通过查阅文献和调研国外实际工程案例发现，不同国家的波纹钢箱涵结构的截面形式略有不同，主要表现在侧墙倾斜角度的不同。美国《AASHTO LRFD 桥梁设计规范》［6］和《澳大利亚/新西兰标准》规范［7］中虽然给出了波纹钢箱涵截面的尺寸参数建议值，但未对侧墙与竖直面的倾斜角度做出规定。《加拿大公路桥梁设计规范》［8］中给出的结构侧墙为直立形。而且多数文献研究了波纹钢箱涵的受力特点［9］和不同加强措施［10］的影响，并没有专门研究截面形式不同对波纹钢箱涵受力和变形性能的影响。

本文使用通用有限元分析软件Abaqus 对波纹钢箱涵侧墙与竖直面夹角分别为0°、5°、10°、15°和20°共5 种截面形式进行建模计算，以分析波纹钢箱涵不同截面形式对结构受力和变形性能的影响。

1 有限元模型的建立和验证

1.1 有限元模型有效性验证

该文以一座跨径6 m、矢高4 m 的波纹钢箱涵试验模型桥为依托，监测回填过程中波纹钢箱涵的变形情况。以试验过程中实测的拱顶竖向位移结果与有限元模型的计算结果对比来验证模型的有效性。该波纹钢箱涵侧墙为直立形，施工过程为自拱脚回填至拱顶以上90 cm。波纹钢板采用Q345 钢材，波形（波长×波高）为381 mm×140 mm，板厚6 mm。

结构左右两侧各取2 倍跨径长度进行计算。波纹钢箱涵长度方向土体采用对称边界条件，模拟土体和结构在平面内可以自由变形。模型左右两侧土体施加竖向滚动支座，约束水平方向位移。下部采取全固定约束。主体波纹钢板采用S4R 单元来模拟，土体采用C3D8R 单元模拟。有限元模型图见图1。

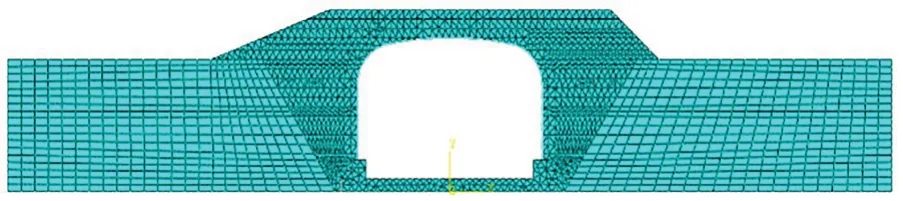
图1 试验桥涵有限元模型图Figure 1 Finite element model of test bridge and culverts

回填过程中波纹钢箱涵拱顶竖向位移与有限元计算值对比如图2 所示。图2 中试验实测值与有限元计算值变化规律一致，数值相近，有限元计算值与实测值最大位移相差仅4.3%，满足精度要求，说明有限元模型能够反映结构的真实受力变形情况，可以做进一步的研究分析。

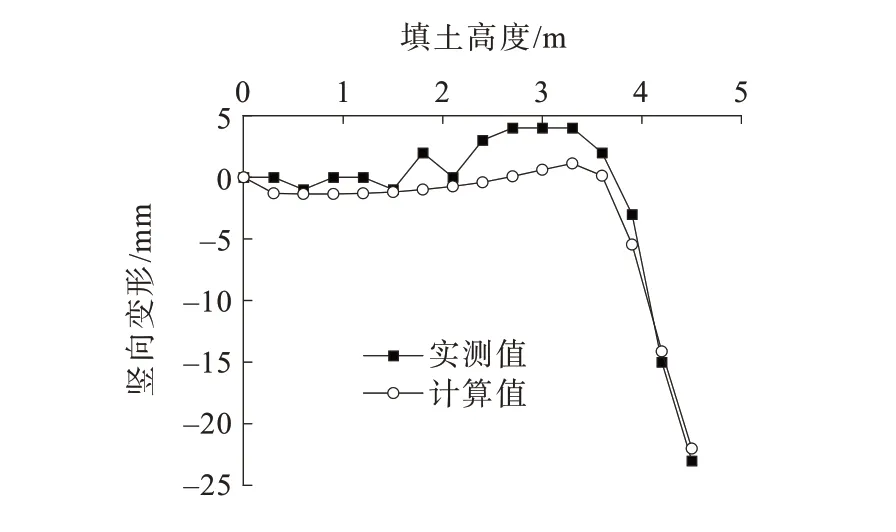
图2 竖向位移实测值与有限元计算值对比Figure 2 Comparison between the measured vertical displacement and that of finite element model

1.2 不同截面有限元模型概述

该文通过使用通用有限元软件对侧墙与竖直面夹角分别为0°、5°、10°、15°和20°时波纹钢箱涵应力和变形进行分析，为以后波纹钢箱涵采取适当的截面形式提供参考。计算波纹钢箱涵跨径均为6 m，矢高均为4 m，波纹钢箱涵5 种截面形式见图3。

图3 截面尺寸图（单位：mm）Figure 3 Dimensions of the sections(unit:mm)

波纹钢板波形（波长×波高×壁厚）尺寸为381 mm×140 mm×6 mm，材质为Q345 钢材。根据《公路波纹钢管（板）桥涵设计与施工规范》（DB 15/T 654—2013）［11］建议要求，对于波纹钢板沿桥宽方向取3 个波长进行建模；对于土体模型，结构左右两侧各取2 倍跨径长度进行计算。主体波纹钢板采用S4R 单元模拟，土体采用C3D8R 单元模拟。有限元计算模型见图4。

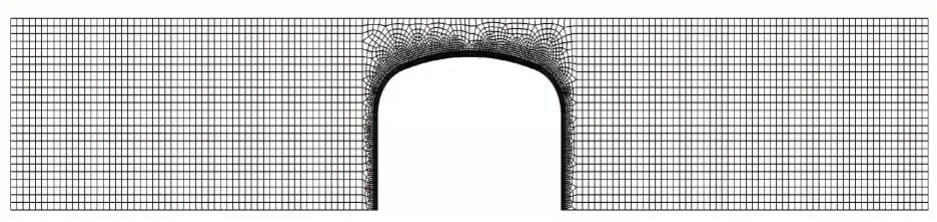
图4 有限元计算模型图Figure 4 Finite Element Calculation Model

1.3 材料、边界条件及荷载

有限元模型中钢材采用双折线本构模型，土体采用摩尔-库仑本构模型，各材料取值见表1。波纹钢箱涵长度方向的土体及波纹钢采用对称边界条件。模型左右两侧土体施加竖向滚动支座，约束水平方向位移。下部采取全固定约束。

表1 有限元模型材料参数取值Table 1 Material parameters in finite element models

荷载为结构自重以及后轴作用于跨中的公路-Ⅱ级车辆荷载（图5）。由于本文取的横桥向长度为3 个波长（3×0.381 m=1.143 m），因此模型范围内仅能布置一个车轮，同时本文参考《公路桥涵设计通用规范》（JTG D60—2015）［12］在单轮荷载的基础上对单轮荷载进行缩放，具体计算方法如式（1）、（2）所示：

图5 施加荷载示意图Figure 5 Schematic diagram of applied load

式中：a为单轴荷载的横向宽度（m）；h为结构的填土高度（m），取1 m；k为单轮荷载的缩放系数；b为模型横桥向宽度，取1.143 m。

2 计算结果分析

为了研究在荷载作用下，不同截面整个断面应力及变形变化情况，现自拱脚位置起每高1 m 布置一个测点，共布置9 个测点，如图6 所示。每个测点分别提取波峰和波谷位置处的应力，本文规定截面轴线中心线外侧为波峰，内侧为波谷，波峰波谷示意图如图7 所示。

图6 测点位置图（单位：mm）Figure 6 Measuring point locations（unit:mm)

2.1 变形计算结果

中载作用下不同截面形式竖向和水平位移如图8 所示，以结构向外变形为正。由图8 可以看出：

图8 中载作用下不同截面形式位移Figure 8 Displacement of different section forms under symmetric loads

（1） 中载作用下不同截面形式均表现为拱顶处的竖向位移较大，且随着倾角的增大，拱顶处的竖向位移明显减小，倾角为0°时，拱顶竖向位移最大，最大竖向位移为27.08 mm；倾角为20°时拱顶竖向位移为3.78 mm，比倾斜角度为0°时降低了86.04%。其余测点的竖向位移基本不变。

（2） 水平方向上拱脚及拱顶水平变形基本为0。倾角为0°时，侧墙及拱肩测点均向外移动，结构基本呈现出拱顶下挠、两侧外凸的状态。随着倾斜角度的增加，侧墙（测点2、3）开始向内移动，分析原因是作用在结构侧墙上的土重增加，导致波纹钢侧墙开始发生内凹。倾角为20°时，结构基本呈现出拱顶下挠、侧墙内凹、拱肩略有外凸的现象。

偏载作用下不同截面形式竖向和水平位移如图9 所示。

由图9 可以看出：加载一侧各测点的竖向位移有所增加，但并不明显，不同截面形式下拱顶竖向位移的变化规律基本与中载一致，最大竖向位移为24.76 mm，位于倾角为0°时的拱顶位置。偏载作用下，不同截面形式波纹钢箱涵的拱顶均朝背离加载点方向发生了水平变形。加载点一侧的结构水平变形明显小于未加载一侧，此时波纹钢箱涵呈现出朝未加载方向整体偏转的状态。

2.2 内力计算结果

中载作用下不同截面形式轴力和弯矩如图10 所示，其中轴力以受压为正，弯矩以外侧受拉为正。

图10 中载作用下不同截面形式内力Figure 10 Internal force of different section forms under symmetric loads

由图10 可以看出：不同截面形式下，轴力始终为正，表明截面始终受压。弯矩图中不同截面的波纹钢箱涵基本处于拱脚外侧受拉、侧墙内侧受拉、拱肩外侧受拉、拱顶内部受拉的状态，这与中载作用下不同截面形式波纹钢箱涵的变形形状一致，基本呈现出侧墙内凹、拱肩外凸、拱顶下挠的现象。随着倾斜角度增加，拱肩处轴力逐渐减小，其余测点轴力变化不明显；倾斜角度为0°时，拱顶的弯矩值最大，最大值为42.14 kN · m，随着倾斜角度的增加，拱顶及拱肩弯矩绝对值逐渐减小，倾角20°时拱顶弯矩比倾角0°减小55.46%，而拱脚处的弯矩值有所增加。

偏载作用下不同截面形式内力如图11 所示。从图11 中可以看出：偏载作用下轴力和弯矩的变化规律与中载基本一致。加载侧各测点的轴力均明显大于未加载侧；加载侧各测点弯矩值仅拱肩处明显大于未加载侧，其余测点弯矩基本对称变化。

图11 偏载作用下不同截面形式内力Figure 11 Internal force of different section forms under eccentric loads

通过对波纹钢箱涵内力结果分析发现：波纹钢结构所受的应力由弯曲应力和轴向应力两部分组成。为研究不同形式波纹钢箱涵结构在加载时到底是弯矩起主导作用还是轴力起主导作用，需要对结构弯曲应力和轴向应力占比进行分析。弯曲应力和轴向应力计算公式如（3）、（4）所示：

式中：σM为弯曲应力（MPa）；σN为轴向应力（MPa）；M为单位长度的截面弯矩（N · m/m）；W为单位长度的截面模量（m³/m）；N为单位长度的截面轴力（kN/m）；A为单位长度的截面面积（m²/m）。

中载和偏载作用下不同截面形式弯矩应力占比如图12 所示。

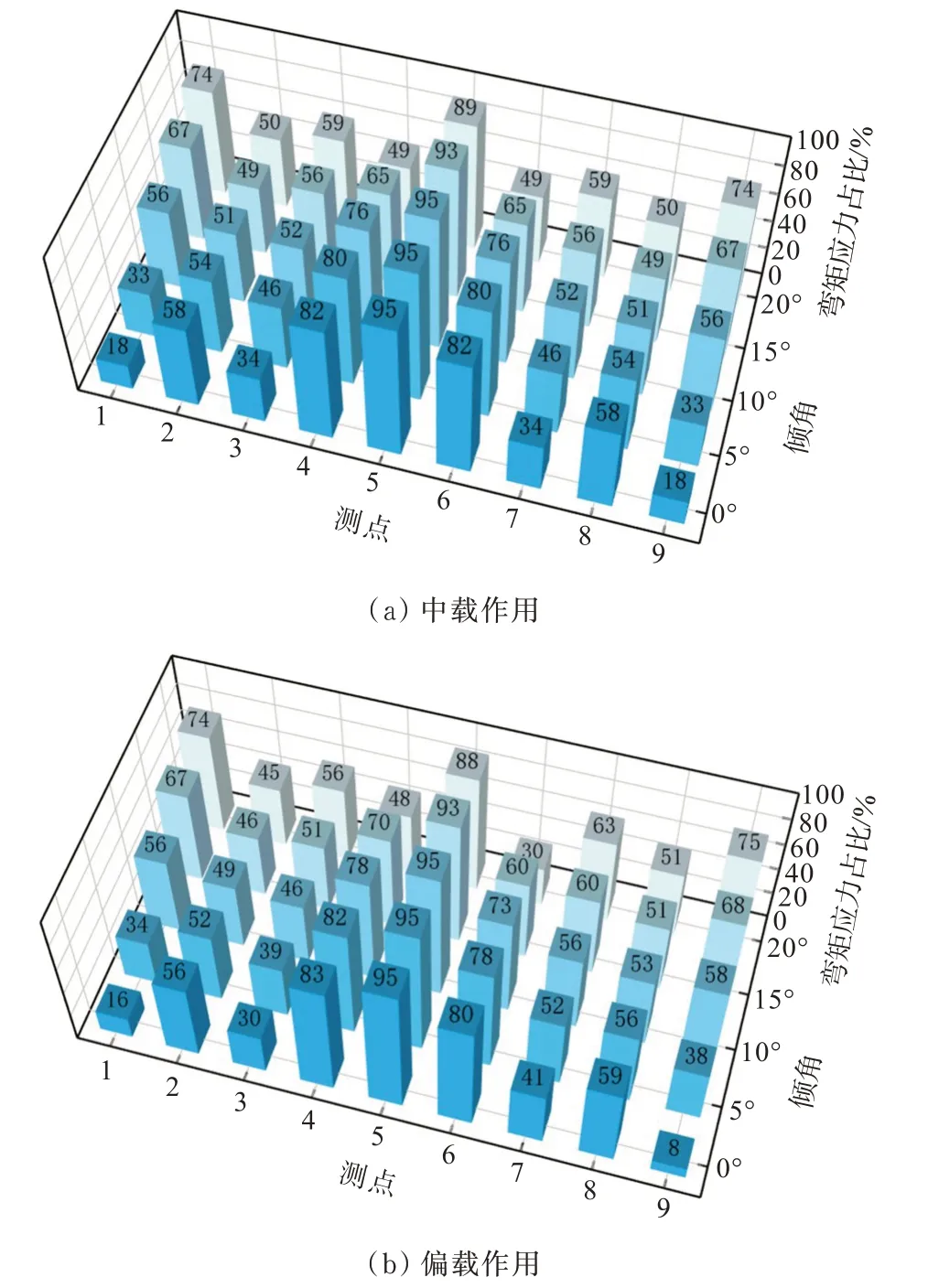
图12 不同截面形式弯矩应力占比图Figure 12 Bending moment stress ratio of different section forms

由图12 可以看出：中载作用下，随着倾斜角度的增加，拱脚处弯曲应力占比明显增加，倾角为20°时，弯曲应力占比达到74%。拱顶弯曲应力有所减小，倾角为20°时弯曲应力占比仍达89%以上。偏载作用下弯曲应力占比变化规律与中载一致，加载侧拱肩处的弯曲应力占比明显要大于未加载侧。结果表明在加载时波纹钢箱涵结构主要受弯矩作用影响，设计时应重点验算结构弯矩效应影响。

2.3 应力计算结果

中载作用下不同截面形式波峰波谷Mises 应力如图13 所示。

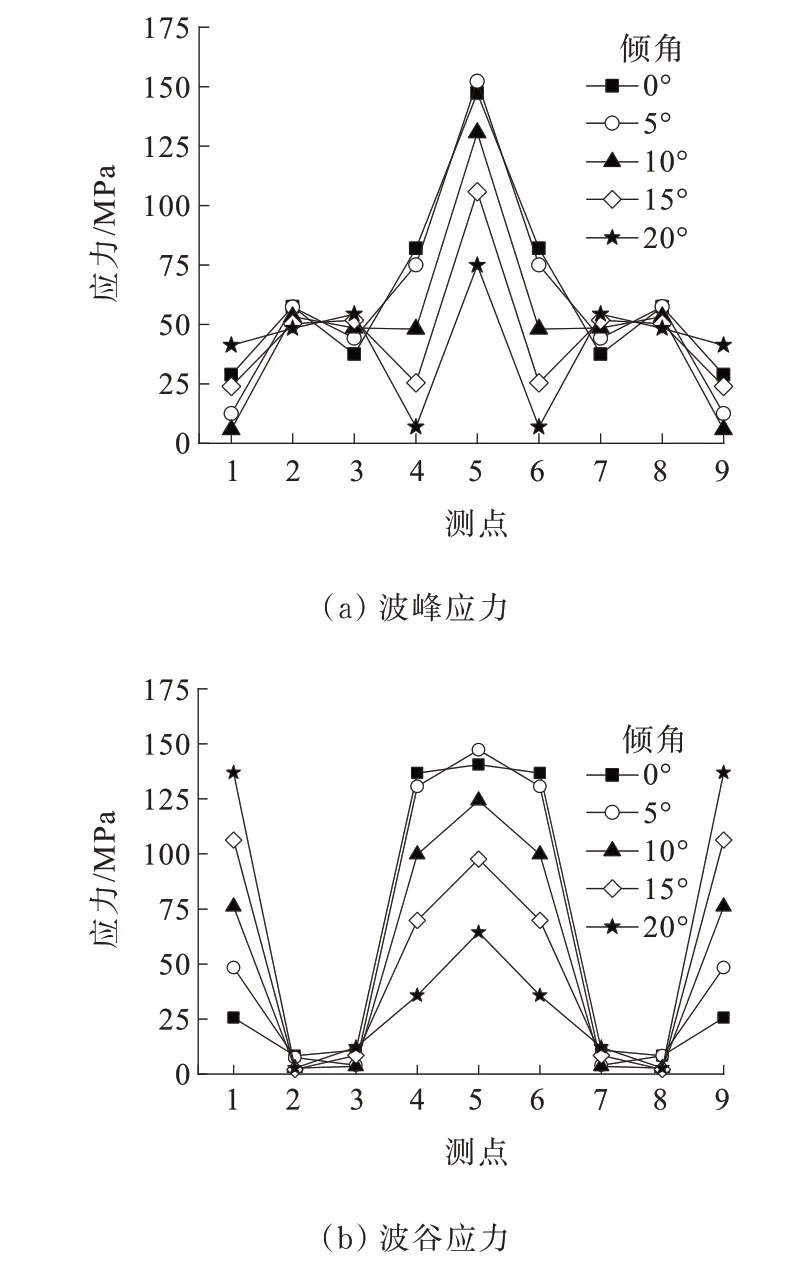
图13 中载作用下不同截面形式波峰波谷应力Figure 13 Crest and valley stress of different section forms under symmetric loads

由图13 可以看出：

（1） 中载作用下，波峰波谷应力关于截面中心对称分布。随着侧墙倾斜角度的增加，侧墙（测点2、3）处的应力变化并不明显，且波谷应力较小。

（2） 拱顶（测点5）和拱肩（测点4）处的Mises 应力随侧墙倾斜角度的增加而减小，其中倾角为0°时拱顶波谷应力出现明显的“削峰”现象，即拱顶处的应力与两侧拱肩的应力相差不大。倾角为5°时结构Mises 应力最大，为152.2 MPa，位于拱顶波峰处。拱脚（测点1）处的波峰应力虽有变化但规律不明显，波谷应力随侧墙倾斜角度增加明显增加，倾角为20°时拱脚处的波谷应力为136.84 MPa，约为倾角为0°的5.3 倍。

偏载作用下不同截面形式波峰波谷应力如图14所示。

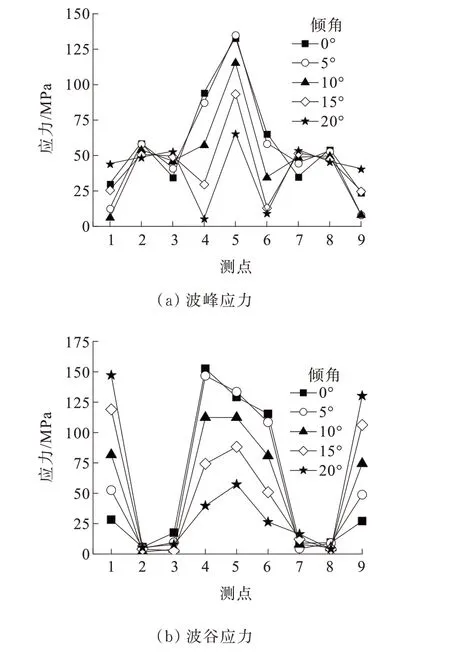
图14 偏载作用下不同截面形式波峰波谷应力Figure 14 Crest and valley stress of different section forms under eccentric loads

由图14 可以看出：偏载作用下，加载侧拱肩处的波峰波谷应力要明显大于未加载侧。倾斜角度为0°时，加载侧拱肩波谷应力为152.56 MPa，超过拱顶应力。随着倾斜角度的增加，拱肩处的波谷应力迅速衰减，逐渐低于拱顶波谷应力，倾斜角度为20°时，加载侧拱肩波谷应力降低至39.7 MPa，比倾斜角度为0°时减小了73.98%。

3 结论

该文通过Abaqus 有限元软件模拟波纹钢箱涵侧墙不同倾斜程度对结构应力和变形的影响，得出以下结论：

（1） 中载作用下，波纹钢箱涵的竖向变形和水平变形关于截面中心线对称变化，结构基本呈现出拱顶下挠、两侧外凸的状态。随着倾角的增大，拱顶处的竖向位移明显减小，倾斜20°时拱顶竖向位移比倾斜角度为0°时降低了86.04%。

（2） 中载作用下，不同截面的波纹钢箱涵基本处于拱脚外侧受拉、侧墙内侧受拉、拱肩外侧受拉、拱顶内部受拉的状态，这与不同截面形式波纹钢箱涵的变形形状保持一致。随着倾斜角度的增加，拱肩处的轴力逐渐减小，其余测点轴力变化不明显；拱顶及拱肩弯矩绝对值逐渐减小，倾角20°时拱顶弯矩比倾角0°减小了55.46%，拱脚处的弯矩值逐渐增加。通过对波纹钢箱涵弯矩应力和轴力应力占比分析发现，随着倾斜角度的增加，拱脚处弯曲应力占比明显增加，拱顶弯曲应力有所减小，但弯曲应力占比仍达89% 以上，设计时应重点验算结构弯矩效应影响。

（3） 中载作用下，波峰波谷应力关于结构截面中心对称分布。随侧墙倾斜角度的增加，拱顶和拱肩处的波峰、波谷应力均逐渐减小，拱脚处的波谷应力明显增加，波峰应力变化不明显。倾角为0°时拱顶波谷应力会出现明显的“削峰”现象，即拱顶与两侧拱肩的应力基本一致。倾角为20°时拱顶最大应力比倾角0°时减小了49.2%。

（4） 偏载作用下，波纹钢箱涵的位移、内力和应力随截面形式的变化规律与中载基本一致，区别在于加载侧拱肩的响应要明显大于未加载侧。为充分发挥波纹钢箱涵截面利用率高的优势，侧墙倾斜角度不宜过大，推荐使用倾斜角度为5°～10°。