基于联合静动力修正的混凝土斜拉桥主梁挠度变化规律研究

李琦，齐东春，杨虎，赵志国

（1.西南交通大学 土木工程学院，四川 成都 610031； 2.国家山区公路工程技术研究中心， 重庆市 400000；3.三峡大学 土木与建筑学院，湖北 宜昌 443002）

0 引言

斜拉桥以其良好的受力性能和优美的造型，得到了广泛的应用，一般认为跨径400 m 以内采用混凝土主梁是最经济的选择［1］。国外1962 年建成的主跨5×235 m 的马拉开波桥为第一座预应力混凝土斜拉桥（以下简称PC 斜拉桥），中国第一座试验性PC 斜拉桥为主跨76 m 的重庆市云阳县汤溪河大桥，于1975 年建成。在中国建成的300 余座斜拉桥中，PC斜拉桥占80%以上。

受各时变因素的影响，PC 斜拉桥主梁线形随服役期的增长不断偏离设计线形，如法国的Broutonne桥服役3 年，主梁跨中下挠近24 cm；中国蚌埠淮河大桥服役期也出现了主梁下挠过大的问题［2］。影响PC斜拉桥线形的时变因素主要包括混凝土徐变、钢束预应力损失、拉索锈蚀与松弛。一般认为徐变是混凝土梁体下挠的主要原因，关于徐变对混凝土主梁线形影响规律的研究较多，主要集中在不同徐变模型预测精度的研究［3-4］。预应力损失被认为是梁体开裂的重要原因，而梁体开裂进一步加剧了梁体下挠，文献主要集中在对不同规范钢束预应力损失计算模式及预应力损失参数取值对主梁受力和线形的研究［5］。关于拉索锈蚀与松弛对结构线形影响的文献不多，Kao 等［6］采用面积折减法模拟拉索锈蚀，分析了不同位置、不同程度、不同数量拉索锈蚀对桥梁结构受力及线形的影响；刘文会等［7］通过拉索松弛试验，得到松弛率与受荷时间的函数关系，采用松弛函数研究拉索松弛对斜拉桥主梁线形的影响规律；田雨金等［8］采用等效温度法模拟拉索松弛行为，计算表明拉索松弛对主梁局部位移影响较大。上述研究在一定程度上揭示了各时变因素对PC 斜拉桥主梁线形的影响规律，但其计算分析均采用基于设计状态的初始有限元模型，未根据服役期实测数据对初始有限元模型进行修正，研究成果具有一定局限性。有限元模型修正实质上是个优化问题，按照修正信息来源的不同，主要分为基于静力的有限元模型修正法、基于动力的有限元模型修正法和联合静动力的有限元模型修正法。联合静动力的有限元模型修正方法包含了静力和动力两个目标函数，克服了单一目标的不足，在实际工程中运用较广泛。Shan 等［9］以实际工程为依托，采用联合静动力的有限元模型修正方法，基于影响面法求解，对桥梁进行有限元模型修正，修正后的有限元模型能更好地反映结构实际状态；秦仙蓉等［10］提出适用于起重机械模型修正的非支配排序遗传算法NSGA-Ⅱ，实现了塔机有限元模型的修正；秦世强等［11］基于改进的遗传算法ISSGA 求解，获得多目标优化问题的局部和全局最优解，实现有限元模型修正。

本文以某主跨450 m 的PC 斜拉桥为工程背景，结合运营期间静动载试验数据，采用联合静动力的有限元模型修正方法，构造双目标优化函数，基于NSGA-Ⅱ算法求解，实现有限元模型修正。在此基础上考虑混凝土徐变、钢束预应力损失及斜拉索松弛等因素的影响进一步研究服役期PC 斜拉桥主梁线形变化规律。

1 工程概况及历年检测情况

某大跨PC 斜拉桥为双塔双索面漂浮体系结构，桥梁跨径为（198+450+198）m。主梁标准横断面采用双主肋截面，梁高2.7 m，梁宽30.6 m，标准肋宽1.8 m，主塔附近肋宽增加至2.6 m，标准节段梁长8.1 m，边支座附近主梁为箱形截面。每个索塔单面1 根吊索，27对斜索，全桥合计220 根索，主梁上索的标准间距为8.1 m，主塔上索的标准间距为1.5 m，斜拉索采用PE防护的镀锌平行钢丝索（直径7 mm，抗拉强度1 670 MPa）。主塔采用C50 混凝土，主墩采用C30 混凝土；主梁15（15′）～23（23′）节段、24′～25′节段、24～27 节段及跨中28 合龙节段为C60 混凝土，其余主梁部分为C50混凝土。该桥结构对称，仅示出半跨立面图（图1）。

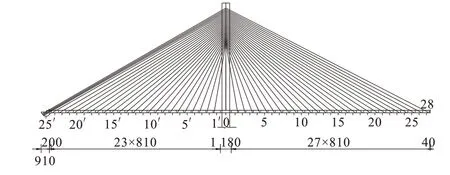
图1 半跨立面图（单位：cm）Figure 1 Half-span elevation(unit: cm)

在成桥时、服役1 年、3 年、5 年、10 年、20 年时，在封闭交通的情况下，对主梁桥面高程进行测量，主梁挠度结果如图2 所示（服役n年主梁挠度实测值=服役n年主梁高程值-成桥主梁高程值）。由图2 可知：随着服役时间的增加，主梁不断下挠，前期变化快，后期变缓，其中跨中位置下挠量最大，服役20 年下挠量为25 cm。

图2 主梁挠度变化图Figure 2 Deflection variation of main girder

2 有限元模型修正

2.1 初始有限元模型建立

采用有限元软件Midas Civil 建立有限元计算模型（图3）。主梁、索塔及桥墩均采用梁单元模拟，斜拉索采用索单元模拟，精确考虑斜拉索在主梁和索塔上的锚固位置，锚固节点与梁塔上的相应节点采用刚臂连接。由于本桥为全漂浮体系结构，在索塔位置主梁节点仅约束侧向自由度，在边墩处主梁节点仅约束竖向自由度，墩底固结。在建立有限元模型时，为反映主梁受力的空间效应，采用梁格法将主梁截面划分为两边主梁+中间桥面板的三主梁模型，以克服单主梁模型中主梁正应力计算的不准确性。各主梁的竖向抗弯惯性矩应按强制移轴定理加以修正以保证其正确性。因主梁为开口截面，模型中各主梁的抗扭惯性矩不用修正。横梁由横隔板与桥面板组成，按实际间距采用等截面梁单元进行模拟。

图3 有限元计算模型Figure 3 Finite element calculation model

按照竣工图实际施工方案建立分阶段有限元计算模型，并按成桥状态的实测索力及实测桥面线形通过施工阶段索力调整及设置主梁预拱度的方式，使计算模型中成桥状态索力及桥面标高与实桥一致。

2.2 有限元模型修正方法

依据静动载试验测试数据，基于NSGA-Ⅱ算法求解，得到Pareto 最优解集，利用最大弯曲角法，从Pareto 最优解集中找到协调最优解，从而实现有限元模型修正［12-14］。

（1） 双目标优化问题

双目标优化问题是有两个目标函数且需要同时优化的优化问题。其数学描述如下：

（2） Pareto 最优解集

对于多目标优化问题，一般不存在唯一的全局最优解，而存在一个最优解的集合，其特点是至少存在一个目标优于其他所有的解，称为Pareto 最优解集。可描述为，当xi优于xj时，满足：

（3） NSGA-Ⅱ算法

NSGA-Ⅱ算法具体步骤为：① 设置NSGA-Ⅱ算法所需要的计算参数，如种群数量、最大进化代数、交叉概率、变异概率；② 随机产生种群规模为N的初始种群P0，并对P0进行非支配排序，求出每个个体的非支配序值及拥挤度，令t=0；③ 采用二元锦标赛法从Pt中选择个体，并进行交叉和变异生成种群规模为N的子代种群Qt；④ 将父代种群Pt与子代种群Qt混合形成种群规模为2N的混合种群Rt；⑤ 求出种群Rt中每个个体的非支配序值和拥挤度，依据选择规则生成新的父代种群Pt+1；⑥ 如果达到终止条件，则算法终止，否则跳转至第③步。

（4） 最大弯曲角法

采用最大弯曲角法，能够高效地从Pareto 最优解集中找到协调最优解。最大弯曲角法求协调最优解如图4所示，曲线为Pareto最优解集，横、纵坐标分别为双目标优化问题的两个目标函数值，x为曲线的最凸点，xL和xR分别为x的相邻左右点，x的弯曲角可表示为：

图4 最大弯曲角法求协调最优解Figure 4 Coordinated optimal solution by the maximum bending angle method

式中：θ为解x的弯曲角；θL、θR为解x与左、右边相邻解xL、xR形成的夹角，计算公式为：

曲线上最凸点为曲线弯曲角最大的点，可认为弯曲角最大点为Pareto 最优解集中的协调最优解。

2.3 修正参数与目标函数确定

经参数敏感性分析并结合本桥的实际情况选择主梁、索塔和主墩的弹性模量及主梁竖向抗弯惯性矩作为模型的修正参数，弹性模量的修正范围取-10%～30%；抗弯惯性矩的修正范围取-10%～0。

选择主梁中跨最大正弯矩工况下主梁位移作为模型修正的静力目标，由于在此工况下，主梁边、中跨位移均比较明显，测试误差影响较小，测试精度能够得到保障，修正效果较好。由于振动频率对结构刚度变化非常敏感，因此选择大桥前7 阶实测自振频率作为模型修正的动力目标。则采用联合静动力的有限元模型修正的目标函数可表示为：

式中：Uaji和Utji分别为第j工况的i点处的有限元模型静力位移理论值和静力位移实测值；γj为第j工况的权重系数；fai和fti分别为桥梁结构自振频率计算值和实测值；n为自振频率阶数。

2.4 有限元模型修正过程及结果

主梁跨中最大正弯矩工况静力位移测点布置如图5 所示。共布置15 个测试断面，每个断面上下游各布置1 个测点，采用高精度水准仪进行测量。模态试验测点布置如图6 所示，共布置38 个测点，每个测点均布置纵向、横向及竖向的3 个方向的高灵敏度加速度传感器。试验采用设置参考测点和分组的方法以获得较为完整的振型。

图5 静力位移测点布置图（单位：cm）Figure 5 Layout of static displacement measuring points (unit: cm)

图6 模态试验测点布置图（单位：m）Figure 6 Layout of measuring points for modal experiment (unit: m)

从初始有限元模型中提取位移值和自振频率值，读入Matlab 编制的遗传算法（NSGA-Ⅱ）程序中进行多目标优化计算，判断优化进程是否满足终止条件，完成模型参数的修正计算。设置NSGA-Ⅱ算法的参数为：种群大小为100，最大迭代次数为100，交叉概率为0.8，变异概率为0.2。得到该问题的Pareto 最优解集如图7 所示。

图7 Pareto 最优解图Figure 7 Pareto optimal solution

利用最大弯曲角法在Pareto 最优解集中找到协调最优解，从而实现有限元模型修正。模型参数修正前后对比见表1。可以得出：模型修正后，主梁混凝土弹性模量增大约26%，索塔混凝土弹性模量增大24.9%，主墩混凝土弹性模量增大24.3%。这与文献［15］的结论一致，主要原因是初始模型中未考虑主梁内配置的较多的普通钢筋和预应力钢束。主梁抗弯惯性矩减小2%，主要是梁体上分布的纵、横向及斜向裂缝降低了主梁刚度。

表1 模型参数修正前后对比Table 1 Comparison of model parameters before and after modification

模型修正前后静力位移及自振频率的实测值与计算值对比见表2、3。

表2 模型修正前后静力位移计算值与实测值对比Table 2 Comparison between calculated and measured values of static displacement before and after model modification

表3 模型修正前后自振频率计算值与实测值对比Table 3 Comparison between calculated and measured values of natural frequency of vibration before and after model modification

由表2、3 可知：修正后的模型计算位移与实测位移数据更加接近，以跨中⑧测点为例，修正前偏差为-6.99%，修正后偏差为0.16%；修正前自振频率相差最大为-12.01%，修正后自振频率相差减小为-1.74%。因此，修正后的有限元模型，能更好地反映结构实际的受力情况。

3 服役期主梁挠度变化规律

运营期PC 斜拉桥受混凝土收缩徐变、预应力损失及斜拉索松弛等时变因素的影响，主梁线形会不断变化。图8 给出了运营20 年后各时变因素对主梁挠度的影响规律，可见混凝土收缩徐变是主梁下挠的主要原因，而预应力损失对主梁线形影响很小，斜拉索松弛对中跨线形有一定影响，跨中最大变形约5 cm。

图8 各时变因素对主梁挠度的影响Figure 8 Influence of time-varying factors on deflection of main girder

由于混凝土徐变的计算模式对计算结果的影响较大，因此在修正模型的基础上，通过几种徐变模式的分析比较以确定较合理的徐变模式，可提高后期变形的预测精度。选择《公路钢筋混凝土及预应力钢筋混凝土桥涵设计规范》（JTG 3362—2018）、CEB-FIP 2010 规范、日本《道路桥示方书2012》（以下简称日本规范）3 种徐变模式进行计算对比分析。

JTG 3362—2018 规范混凝土收缩徐变预测模式中，收缩应变等于名义收缩系数乘以收缩随时间发展的系数；徐变系数用一个双曲幂函数来计算，为名义徐变系数乘以其随时间变化的系数；CEB-FIP 2010 规范混凝土收缩徐变预测模式将收缩分为基本收缩和干燥收缩，徐变也分为基本徐变和收缩徐变，采用求和方式计算收缩徐变；日本规范使用的收缩模式采用基本收缩应变乘以随时间变化的系数，徐变模式采用相对滞后弹性变形徐变和相对流变徐变相加的方式。不同模式收缩应变及徐变系数计算公式见表4，表4 中各公式参数含义详见相关规范。

表4 收缩徐变计算公式Table 4 Calculation formulas of shrinkage and creep

对于拉索松弛问题，刘文会等［7］通过试验拟合了拉索应力松弛率μ与受荷时间t的关系：

采用不同的徐变模式，并计入拉索松弛效应的影响，采用修正后的模型计算主梁的后期变形，并与历年主梁线形实测数据进行比较，结果如图9～11 所示。计算结果分析表明：不同计算模式计算结果存在一定差异，与实测值对比分析可知，基于修正后的模型，采用CEB-FIP 2010 规范计算挠度与实际挠度更加接近，日本规范计算误差偏大，JTG 3362—2018 规范计算误差介于两者之间。按日本规范徐变模式计算得到的变形值均大于实测值，按CEB-FIP 2010 规范计算的变形值前期与实测值接近，后期大于实测值。

图9 JTG 3362—2018 规范主梁挠度变化图Figure 9 Deflection variation of main girder in JTG 3362—2018 specification

由图10 可知：随着服役时间的增加，主梁不断下挠，前期变化快，后期变缓；跨中位置下挠量最大，服役20 年下挠量约为270 mm。

图10 CEB-FIP 2010 规范主梁挠度变化图Figure 10 Deflection variation of main girder in CEB-FIP 2010 specification

图11 日本规范主梁挠度变化Figure 11 Deflection variation of main girder in Japan specification

基于修正模型，按CEB-FIP 2010 规范的徐变模式并考虑拉索松弛时变因素，分析预测该混凝土斜拉桥服役5 年、10 年、20 年、30 年、40 年主梁挠度的变化规律，结果如图12 所示。

图12 基于修正模型的主梁挠度变化图Figure 12 Deflection variation of girder based on modified model

由图12 可见：随着服役时间的增加，主梁不断下挠，其中主梁中跨跨中下挠最明显。该桥服役5 年，主梁跨中下挠约164 mm；服役10 年，主梁跨中下挠约214 mm，服役20 年，主梁跨中下挠约270 mm。前20 年的计算结果基本与实测数据相吻合。按此模型可预测服役30 年，主梁跨中下挠约305 mm；服役40年，主梁跨中下挠约326 mm。主梁跨中挠度前5 年平均增长率达33 mm/年，在30～40 年之间跨中挠度平均增长率为2.2 mm/年。前5 年主梁跨中挠度占前40 年的50%。PC 斜拉桥主梁下挠变形基本上可以持续30 年左右，前10 年下挠量大，后20 年下挠慢，最后逐渐趋于平稳。另外，对于PC 斜拉桥徐变对中跨线形影响较大，而对边跨线形影响较小，边跨最大徐变变形仅30 mm，约为中跨的1/10。

4 结论

本文以某在役PC 斜拉桥为工程依托，采用联合静动力的有限元模型修正法，以该桥静动载试验实测数据为目标，构造双目标优化问题，基于NSGA-Ⅱ算法求解，得到pareto 最优解集，采用最大弯曲角法从pareto 最优解集中找到协调最优解，实现有限元模型修正。在此基础上，采用不同混凝土徐变模式并计入拉索松弛效应，结合历年主梁线形监测数据，研究PC 斜拉桥服役期主梁挠度变化规律。得出如下主要结论：

（1） 模型修正后，主梁、索塔及主墩混凝土弹性模量均有较大幅度增加，增幅超过20%，而主梁抗弯惯性矩减小2%，这与其他文献的研究结论一致。修正后有限元模型的位移与自振频率的计算值与实测值更加接近，说明修正后的模型能更好地反映桥梁结构实际状态。

（2） 在修正模型的基础上，采用不同徐变模式对服役期主梁的挠度进行了计算，并与历年主梁线形实测数据进行对比分析。不同计算模式计算结果存在一定差异，采用CEB-FIP 2010 规范计算挠度与实际挠度更加接近。中跨跨中位置下挠量最大，服役20 年下挠量约为270 mm，与实测值基本吻合。

（3） 采用修正模型分析了服役期主梁线形的变化规律，并预测了未来20 年主梁线形变化趋势，研究表明：主梁跨中挠度前5 年平均增长率达33 mm/年，在30～40 年之间跨中挠度平均增长率为2.2 mm/年。前5 年主梁跨中挠度占前40 年的50%，后期主梁下挠趋于平缓。