基于概率性时序生产模拟的光储网协调规划

商经锐，刘建飞，李贵良，唐立军，赵 静

（云南电网有限责任公司德宏供电局，德宏 678400）

能源危机和环境问题的不断加剧，促使分布式光伏发电得到了快速发展[1-2]。由于负荷本身具有随机波动特性，分布式光伏的大量接入使得配电网规划所面临的源荷不确定性问题更加突出[3-4]。因此，深入挖掘源荷的概率分布特性，充分发挥分布式光伏、储能与配电网络的资源互补优势，对实现有源配电系统的精准投资和经济运行具有重要意义。

近年来，许多学者采用场景聚类[5]的方法来研究源荷的不确定性。文献[6]利用并行迭代二分Kmeans-+聚类方法进行分布式光伏和负荷的不确定性场景缩减；文献[7]利用模糊C-均值聚类方法进行分布式光伏和负荷的场景划分；文献[8]利用层次聚类对天气类型进行聚类进而实现光伏出力的预测；文献[9]为解决多概率场景的分析问题，提出一种融合K-means 聚类和层次聚类形成复合聚类的场景压缩方法。虽然K-means 聚类[10]、模糊C-means 聚类[11]、层次聚类算法[12]等场景缩减方法在处理源荷不确定性时具有一定成效，但存在初始聚类中心选择困难、相似度衡量带有偏差等问题，导致聚类结果难以准确反映源荷时序运行情况，进而影响规划投资的精准性。也有部分学者尝试采用概率模型来表征源荷的不确定性。文献[13]采用Beta分布来表示光伏出力的概率密度；文献[14]提出了一种兼顾Beta 模型与非参数核密度估计的综合概率建模方法；文献[15]提出了一种极值负荷及其出现时刻的概率化模型；文献[16]通过在各种确定性规律基础上叠加相应的随机波动性来建立随机变量的概率模型，以此来描述源荷的不确定性。但目前的概率模型均针对的是系统典型运行断面，对于源荷在长周期时序上的波动性及相关性欠缺考虑。

分布式光伏的快速发展给配电系统带来挑战，同时也提供了大量的规划资源，尤其是将分布式光伏、储能与配电网架进行联合优化配置，使得光伏与储能的联合出力曲线与负荷曲线匹配，尽可能地削减负荷的尖峰、平抑负荷的波动，由此可大幅提升配电系统的规划精准性和运行经济性。文献[17]建立了考虑分布式电源与负荷不确定性的多状态模型，提出了一种基于机会约束规划的分布式电源与配电网架多目标规划方法。文献[18]提出一种基于经济性的分布式光伏和储能协同优化配置模型；文献[19]提出了一种含光伏的低压配电网分布式储能多目标优化配置方法；文献[20]提出了一种考虑运行控制策略的广义储能资源与分布式电源联合规划方法，侧重于不同储能资源与分布式电源的配合运行；文献[21]基于实际配电网“闭环设计、开环运行”的特征，提出了一种考虑N-1安全准则的配电网与分布式储能联合规划方法，侧重于储能与配电网网架在安全供电方面的配合。当前的研究在进行配电系统规划时，未能充分挖掘源网荷储的协同优势，而且都是以典型运行断面为基础来进行优化，忽略了分布电源出力与负荷的时序相关性，对于系统全时段概率运行状态的估计会产生一定的误差。

基于此，本文提出一种基于源荷概率性时序生产模拟的光储网协调规划方法。针对负荷与分布式光伏出力的不确定性，建立源荷概率性时序序列模型，利用生产模拟技术求取配电系统年运行概率状态；同时综合考虑光伏、储能、配电网的投资与运行损耗、停电损失、弃光损失及向上级电网的购电成本，建立基于随机优化的综合协调规划模型，通过投资决策与运行模拟两阶段的迭代寻优获得能够适应不确定因素的最优规划方案，实现配电系统的精准投资与经济运行。

1 概率性时序序列模型

负荷与分布式光伏出力具有不确定性，利用概率性时序序列[22-23]可以较好地描述其在时间维度的随机性和波动性。以下以负荷为例具体说明概率性时序序列模型的构建方法。

1.1 概率性时序序列矩阵构建

通过对历史数据的统计分析及归一化处理，可以得到负荷曲线的离散概率分布特性。以小时级别取年负荷8 760 个小时点数据，由于日负荷曲线在各个季节变化较大，而在每个月内变化不大，所以可以将全年负荷简化为12个月24个时刻点的随机变量矩阵PLoad，即

式中：PLoad为负荷全年12个月24个时刻点的随机变量矩阵；Pm,t为第m个月第t时刻点负荷随机变量的历史数据矩阵。

将PLoad进行概率序列化，可得年负荷曲线的概率序列化矩阵A为

式中：A为年负荷矩阵PLoad的概率序列化矩阵；Am,t为第m个月第t时刻点的负荷概率序列矩阵，可表示为

式中：Am,t是一个2LAm,t的矩阵，用于描述m个月第t时刻点负荷的离散概率分布，其中LAm,t为概率分布序列Am,t的长度；iAm,t为负荷概率分布序列区间序号。Am,t的第1 行是负荷离散值对应的概率，第2行是负荷随机变量的离散值，即Am,t(1,iAm,t)为负荷离散值Am,t(2,iAm,t)对应的概率。

1.2 概率序列的生成方法

概率序列Am,t的生成方法可通过以下两步完成。

（1）确定离散概率序列分布的长度，选取离散化因子。定义概率序列分布的长度LAm,t为

式中，和分别为离散变量Pm,t的最大值和最小值。离散化因子是随机变量Pm,t转换为概率序列的离散化步长，步长越小，量化误差越小，计算精度越高，但计算量越大。考虑到计算效率和数据精度，离散化因子一般选择离散变量Pm,t样本空间的最大公约数。

（2）以为区间长度，将Pm,t的变化范围分为LAm,t个等长区间，分别统计落入各离散化区间的数据期望值，作为对Pm,t在该离散化区间取值的估计；并分别统计各离散化区间变量Pm,t出现的频率，作为对Pm,t落入该离散化区间概率的估计。Pm,t的离散概率分布矩阵Am,t可用公式计算为

式中：niAm,t为Pm,t落入第iAm,t个区间内的个数；Em,t为Pm,t在第iAm,t个区间的期望值；Pm,t,j为Pm,t在第iAm,t个区间的第j个样本值；θ为离散变量Pm,t概率分布的起始参数，保证概率分布从Pm,t的最小值所在的区间开始，避免了概率分布起始部分概率为0值的情况；Nm,t为离散变量Pm,t的数据总量。其中，样本数据可取待规划改造区域或邻近类似区域的近5年的8 760 h年负荷数据。

同理，分布式光伏的概率性时序序列矩阵B的构建与负荷A的类似，由此可得第m个月第t时刻点分布式光伏的离散概率分布矩阵Bm,t，即

式中：Bm,t是一个2LBm,t的矩阵，用于描述第m个月第t时刻点分布式光伏出力的离散概率分布，其中LBm,t为概率分布序列Bm,t的长度；iBm,t为光伏出力概率分布序列区间序号；Bm,t的第1 行为分布式光伏出力离散值对应的概率，第2行为分布式光伏出力变量的离散值，即Bm,t(1,iBm,t)为分布式光伏出力离散值Bm,t(2,iBm,t)对应的概率。

2 基于随机规划的光储网协调规划模型

电力系统规划是在满足电力需求的基础上，确定最佳的系统建设方案。然而，由于存在负荷与光伏出力等不确定性因素，可能导致确定性优化的最优解在运行时并非最优方案，甚至可能因不确定性引起电力系统结构不合理，进而导致事故发生。为解决此问题，本文提出一种光储网两阶段随机优化方法[24-25]，第1阶段为投资规划决策，变量为光伏、储能及电网的投资决策量；第2 阶段为系统运行优化，利用源荷概率性时序生产模拟来反映规划方案对光伏和负荷随机波动的适应性，具体体现在运行网损、停电损失、弃光损失及向上级电网的购电成本，其光储网协调规划具体流程如图1所示。通过两阶段的迭代寻优得到能够适应不确定因素的最优规划建设方案。

图1 基于概率性时序生产模拟的光储网协调规划流程Fig.1 Flow chart of coordinated planning for photovoltaic,energy storage and distribution network based on probabilistic time series production simulation

综合考虑光伏、储能、配电网的投资与运行损耗、停电损失、弃光损失及向上级电网的购电成本，建立基于随机规划的光储网的协调规划模型，其目标函数表示为

式中：CTotal为系统年综合成本费用；CPv为光伏的年投资成本和运维成本；CEs为储能的年投资成本和运维成本；CDis为配电网的年投资成本和运维成本；CGloss为系统的年网络损耗费用；CReli为系统的年停电损失；CPvloss为系统的年弃光损失；CEn为配电系统向上级电网的购电成本；X为决策变量集，即光伏和储能的接入位置及容量，配电网线路及配变的新建与改造等变量构成的集合；ξ为配电系统的随机变量的概率状态空间。

（1）配电网建设的年综合成本为

式中：Nlr、Nln、Nbr、Nbn分别为现有线路、新建线路、现有配变、新建配变总数；xk、xm、xn、xq为0-1变量，0 表示未被选中，1 表示被选中；ClrUnit,k、ClnUnit,m、CbrUnit,n、CbnUnit,q分别为改造线路、新建线路、改造配变、新建配变的单位成本；Llr,k、Lln,m、Sbr,n、Sbn,q分别为改造线路长度、新建线路长度、改造配变容量、新建配变容量；Wlr,k、Wln,m、Wbr,n、Wbn,q分别为改造线路、新建线路、改造配变、新建配变的运行维护费，本文取建设投资成本的5%。

（2）光伏年综合成本为

式中：NPv为安装光伏候选位置节点的总数；xi为0-1变量，0表示第i个拟安装节点未被选中，1表示被选中；CPvUnit,i为在第i个候选位置所安装光伏的单位容量投资成本；SPv,i为安装在第i个候选位置的光伏安装容量；WPv,i为安装在第i个候选位置的光伏运行维护费，本文取建设投资成本的5%。

（3）储能年综合成本为

式中：NEs为安装储能候选位置节点的总数；xj为0-1变量，0表示第j个拟安装节点未被选中，1表示被选中；CEUnit,j为在第j个候选位置所安装储能的单位容量成本；CPUnit,j为在第j个候选位置所安装储能的单位功率成本；SEs,j为安装在第j个候选位置的储能安装容量；PEs,j为安装在第j个候选位置的储能的额定功率；TEs,j为安装在第j个候选位置的储能在额定功率下的充放电时长；由于储能容量等于额定功率与充放电时长的乘积，所以在工程建设时，一般可将单位功率成本折算成以单位容量计价的成本，即CEsUnit,j为在第j个候选位置所安装储能的单位容量综合投资成本，包括单位容量成本CEUnit,j和经过折算后的单位功率成本CPUnit,jTEs,j；WEs,j为安装在第j个候选位置的储能运行维护费，本文取建设投资成本的5%。

（4）系统的年网络损耗为

式中：CGlossUnit为网络损耗的单位成本；PGloss为网络有功损耗量。

（5）系统的年停电损失为

式中：NLoad为负荷节点个数；CLoad,i为负荷节点i的单位停电损失；αit为0-1变量，0表示负荷节点i在t时刻没有处于停电状态，1 表示处于停电状态；PLoad,it为负荷节点i在t时刻的负荷。

（6）系统的年弃光损失为

式中：βit为0-1变量，0表示节点i安装的光伏在时刻t没有处于弃光状态，1 表示处于弃光状态；CPv,it为节点i安装的光伏在t的时刻单位上网电价；PPvloss,it为节点i安装的光伏在t时刻的出力。

（7）向上级电网的年购电成本为

式中：CEnUnit为向上级电网购电的单位电价；PTotal,t为t时刻配电系统的总负荷；PPv,it为节点i安装的光伏在t时刻的出力。

本文搭建的光储网协调规划模型约束条件主要考虑系统的供电可靠性约束、新能源消纳率约束、支路功率约束、配变容量约束、节点电压约束、功率平衡约束和储能充放电功率约束，具体计算公式如下。

（8）供电可靠性约束为

式中：Rs(X,ξ)为系统在年概率状态空间ξ下的供电可靠率；为向社会承诺的最低供电可靠率。

（9）新能源消纳率约束为

式中：SCR(X,ξ)为系统在年概率状态空间ξ下的新能源消纳率；SCRmin为向社会承诺的最低新能源消纳率。

（10）支路功率约束为

式中：Pl,k(X,ξ)为系统在年概率状态空间ξ下支路k的有功功率；为支路k的有功功率允许最大值；ΩLine为系统支路集合。

（11）配变容量约束为

式中：Pb,n(X,ξ)为系统在年概率状态空间ξ下第n台配变的负载；为第n台配变的负载最大值。

（12）节点电压约束为

式中：Ui(X,ξ)为系统在年概率状态空间ξ下节点i的电压；、分别为节点i的电压上、下限；ΩNode为系统节点集合。

（13）功率平衡约束为

式中：Pi、Qi分别为节点i注入的有功功率和无功功率；Gij、Bij、δij分别为节点i、j之间的电导、电纳和电压相位差；NNode为系统节点总数；Ui、Uj分别为节点i、j的电压幅值。

（14）储能充放电功率约束。储能在运行中的任一时段只能处于充电或放电状态，且充放电功率不应超过其额定值，即

式中：为安装在j节点的储能的额定功率；和分别为安装在j节点的储能在t时刻的充电和放电功率。

3 源荷概率性时序生产模拟

3.1 系统年运行概率状态求解方法

当系统的电网结构一定时，系统的状态由源荷的状态组合决定，在求解系统年运行概率状态之前，需对概率状态矩阵的卷和运算[26]进行扩展定义。

设概率状态矩阵Z和Z′分别为

式中：LZ和LZ′分别为Z和Z′的长度；nZ和nZ′分别为Z和Z′的行数；iZ为Z的第iZ列，表示概率状态矩阵Z中的第iZ个状态；iZ′为Z′的第iZ′列，表示概率状态矩阵Z′中的第iZ′个状态。两个概率状态矩阵中，第1 行是系统状态的概率，即Z(1,iZ)（或Z(1,iZ′)）为系统在第iZ（或iZ′）个状态的概率，第2行至第nZ（或nZ′）行是系统状态概率对应的状态量的值，即Z(jZ,iZ)（或Z(jZ′,iZ′)）为系统在第iZ（或iZ′）个状态下第jZ（或jZ′）个状态量的值。

设概率状态矩阵φ为Z和Z′的卷和运算结果，即

式中：iφ为φ的第iφ列，表示概率状态矩阵φ中第iφ个状态；Lφ和nφ分别为概率状态矩阵φ的长度和行数，可通过公式计算为

φ中第1行的状态概率为两个状态卷和矩阵状态概率的乘积，φ中对应的第2行至第nφ行的状态值则等于两个状态卷和矩阵对应的状态值的和，分别表示为

式中：φ(1,iφ)为概率状态矩阵φ在第iφ个状态的概率；φ(jφ,iφ)(jφ＞1)为概率状态矩阵φ在第iφ个状态下第jφ个状态量的值。

因此，对负荷与光伏第m个月第t时刻的概率状态矩阵Am,t、Bm,t进行卷和即可得系统第m个月第t时刻的概率状态矩阵ξm,t，即

结合目标函数的求解与系统运行生产模拟产生的状态量，可对ξm,t进行扩展，即

式中：iξm,t为概率状态矩阵ξm,t中的第iξm,t个状态；Lξm,t为概率状态矩阵ξm,t的长度，可表示为

ξm,t的第1 行是系统状态概率，ξm,t(1,iξm,t)为系统在第iξm,t个状态（即负荷为Am,t(2,iAm,t)、光伏出力为Bm,t(2,iBm,t)）的概率，即

ξm,t的第2、3、4、5 行分别表示系统状态的停电指标集、弃电指标集、网损和向上级电网的购电量。

系统在第iξm,t个状态的停电指标集ξm,t(2,iξm,t)可表示为

式中，ξm,t(2,iξm,t)(1)、ξm,t(2,iξm,t)(2)、ξm,t(2,iξm,t)(3)分别表示该状态下发生停电的用户数、停电时长、损失负荷。

系统在第iξm,t个状态的弃电指标集ξm,t(3,iξm,t)可表示为

式中，ξm,t(3,iξm,t)(1)、ξm,t(3,iξm,t)(2)分别为该状态下光伏的弃电量和发电量。系统在第iξm,t个状态的网损为ξm,t(4,iξm,t)，系统在第iξm,t个状态向上级电网的购电量为ξm,t(5,iξm,t)。由此即可求得系统全年的概率状态矩阵ξ为

3.2 概率性时序生产模拟过程

本文采用混合编码遗传算法进行光储网的规划方案寻优，编码规则见表1。其中，分布式光伏的接入位置与容量、储能的接入位置与容量均采用整数编码，线路新建、改造和配变新建、改造的信息均采用二进制编码。

表1 染色体编码规则Tab.1 Chromosome coding rule

种群迭代过程中则利用源荷概率性时序序列对系统全年运行状态进行概率性时序生产模拟，从而进行目标函数的计算与约束条件的校验，具体流程详见图1。

（1）由光伏、负荷历史数据分别生成源荷离散概率化序列A、B。

（2）构建系统状态概率矩阵ξm,t，状态数为光伏与负荷的状态数的乘积，对应的状态概率为光伏与负荷对应状态的概率乘积。

（3）求取第m月（初始m=1）的状态概率矩阵。

（4）求取第m月第t时刻（初始t=1）的状态概率矩阵。

（5）从负荷概率序列Am,t中取第t时刻的第iAm,t组（初始iAm,t=1）概率状态。

（6）从光伏概率序列Bm,t中取第t时刻的第iBm,t组（初始iBm,t=1）概率状态。

（7）判断各支路在负荷第iAm,t状态、光伏出力第iBm,t状态下是否会发生停电现象，判据为：（支路有功负荷-支路光伏出力-支路可用储能最大出力）＞支路最大允许功率。如果是，判断切负荷量，将停电的用户数、停电时长、损失负荷放入ξm,t(2,iξm,t)。

（8）判断各支路在该状态下是否会发生弃光现象，判据为：（支路光伏出力-支路有功负荷-支路可用储能最大充电功率）＞支路最大允许功率。如果是，判断弃光量，将光伏弃电量和发电量放入ξm,t(3,iξm,t)。

（9）修正该状态下系统的负荷输入与光伏输入，即将第（7）步和第（8）步发生的停电负荷和弃光的光伏切除。

（10）计算该状态下的系统潮流，将计算得到的网损和向上级电网的购电量分别放入ξm,t(4,iξm,t)和ξm,t(5,iξm,t)。

（11）令iBm,t=iBm,t+1，转至第（6）步，循环迭代，直至iBm,t=LBm,t。

（12）令iAm,t=iAm,t+1，转至第（5）步，循环迭代，直至iAm,t=LAm,t。

（13）令t=t+1，转至第（4）步，循环迭代，直至t=24。

（14）令m=m+1，转至第（3）步，循环迭代，直至m=12，最终得到系统全年的概率状态矩阵ξ。

（15）基于系统全年概率状态矩阵，对每个染色体对应的规划方案进行目标函数计算及约束条件校验，进而进行种群迭代寻优，直至满足搜索终止条件。

4 算例分析

4.1 算例介绍

选取某个实际配电网为例进行仿真分析，拓扑结构如图2 所示，该配电网共有20 个节点、19 条线路，变压器容量为500 kV·A，变比为10 kV/0.4 kV，各节点规划年预测负荷最大值如表2 所示，各支路阻抗如表3 所示。表4 给出了涉及的相关参考价格。

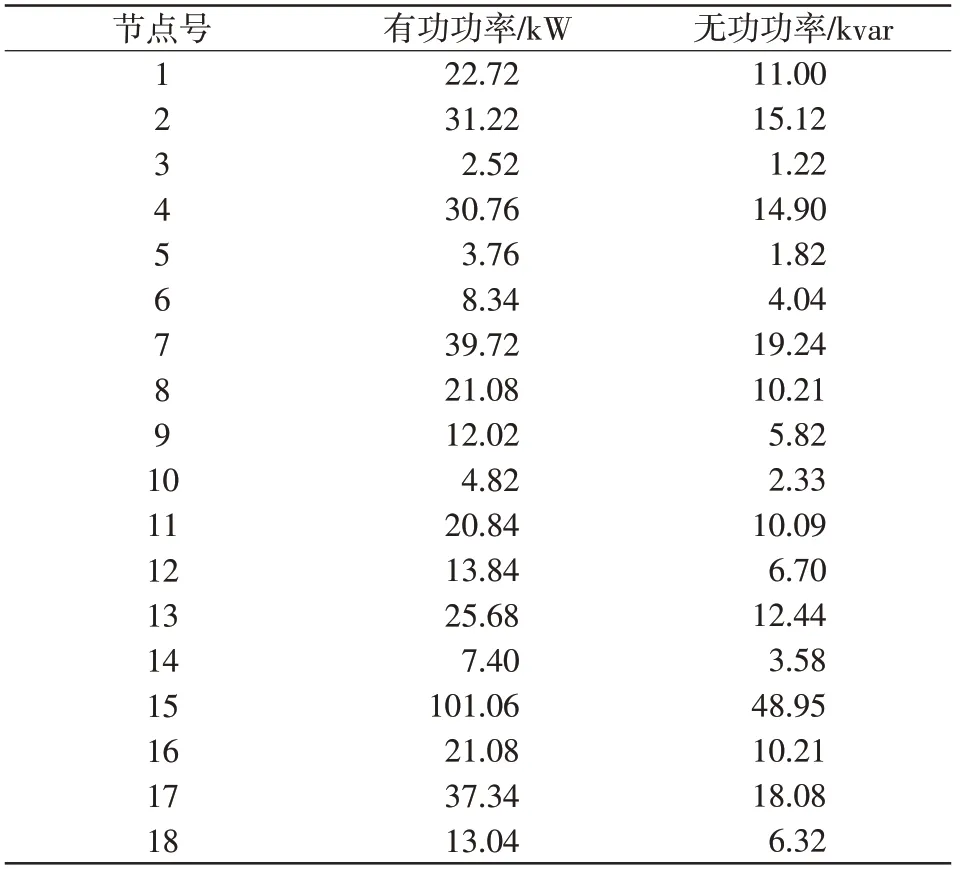
表2 各节点规划年预测负荷最大值Tab.2 Maximum predicted annual load at each node

表3 各支路阻抗Tab.3 Impedance of each branch

表4 相关参考价格Tab.4 Related reference prices

图2 某实际配电网拓扑结构Fig.2 Topological structure of one actual distribution network

4.2 结果分析

4.2.1 规划方案比较

本文分3 种情形对规划方案进行比较分析。情形1：按照系统最大负荷运行断面的传统配电网规划；情形2：基于场景聚类的分布式光伏与配电网网架的概率规划；情形3：基于概率性时序生产模拟的分布式光伏、储能与配电网网架的协调规划。通过仿真计算，规划结果及年综合费用情况如表5和表6所示。

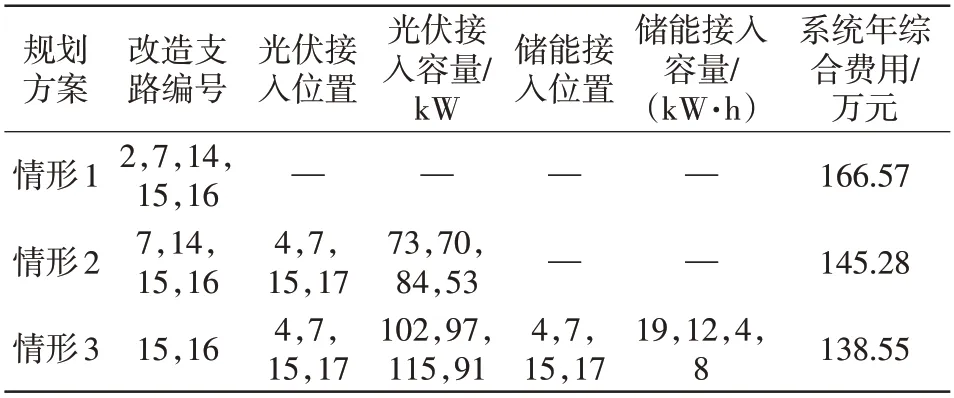
表5 3 种情形的规划方案Tab.5 Planning schemes in three cases

表6 3 种情形规划方案的分项成本Tab.6 Itemized cost under planning schemes in three cases 万元

分析表5 中各情形优化结果可以发现，情形1因未考虑分布式光伏和储能的接入，且采用传统基于最大负荷预测断面的规划方法，为应对负荷的不确定性，需要改造的线路均比情形2 和情形3 多。对比情形2 和情形3 可以看出，情形2 由于只进行了典型聚类场景的优化，忽略了源荷长周期时序的相关性，且未考虑储能的接入，其光伏接入容量要少于情形3，而系统年综合费用却多于情形3；而情形3 由于利用概率性时序生产模拟实现了光储网的最优化配置，改造线路条数比情形1 和情形2 均要少，且年综合费用分别比情形1 和情形2 降低了16.82%和4.63%。

对比表6 中的各项成本可以看出，除投入分布式光伏和储能后增加相应建设成本外，情形2和情形3的4个分项成本：配电网建设成本、网络损耗费用、系统停电损失、向上级电网的购电成本，均比情形1有所降低，配电网建设成本分别降低29.53%和73.83%，网络损耗费用分别降低30.32%和36.77%，系统停电损失分别降低93.84%和97.63%，向上级电网的购电成本分别降低17.11%和24.51%。情形3由于采用了概率性时序生产模拟来进行资源配置，促进了源荷特性在长周期时序中的优化匹配，使得配电网的建设成本和运行成本都得到大幅度的降低。

利用本文基于概率性时序生产模拟方法所得到的光储网规划方案不仅降低了系统年综合费用，在提升设备利用率方面也具有一定优势。图3～图5给出了情形3与情形1各支路月度平均利用率的具体情况。支路月度平均利用率是指该支路在计算月份内各时刻点负载率的平均值，如支路k第m月的平均利用率Um,k可表示为

图3 情形3 中各支路的月度平均利用率Fig.3 Monthly average utilization of each branch in Case 3

图4 情形1 中各支路的月度平均利用率Fig.4 Monthly average utilization of each branch in Case 1

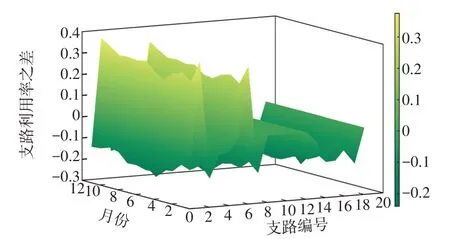
图5 情形3 与情形1 的支路月度平均利用率之差Fig.5 Difference between monthly average utilizations of each branch in Cases 3 and 1

式中：Dm为第m月的天数；Uk(d,t)为支路k第d天第t时刻的负载率。

对比图3～图5 可以看出，相比于情形1，情形3由于采用了基于概率性时序生产模拟方法来进行光储网的优化配置，规划方案可以较好地适应负荷的波动，利用分布式光伏和储能的出力能够有效地削减负荷尖峰，同时储能具有移峰填谷作用，使得设备运行始终保持在较高利用水平。可见，利用本文所提方法进行分布式光伏与储能的合理接入，可以使得规划方案投资更精准、运行更经济。

4.2.2 负荷尖峰特性对规划方案的影响

本文利用年负荷率（年负荷率=年平均负荷/年最大负荷）指标来表示负荷的尖峰特性。在年电量相同的情况下，年负荷率越低表示负荷的尖峰特性越明显。图6给出了年负荷率从70%到40%变化过程中3种情形的年综合费用情况。同时，在系统运行方面，随着年负荷率的变化，图7和图8分别给出了部分支路在情形3和情形1中的年度平均利用率。

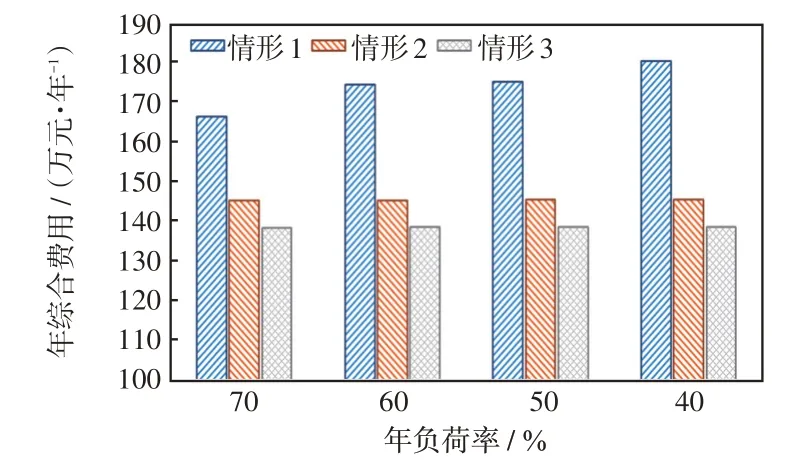
图6 不同年负荷率情况下3 种规划方案的年综合费用比较Fig.6 Comparison of annual comprehensive costs among three planning schemes at different annual load rates

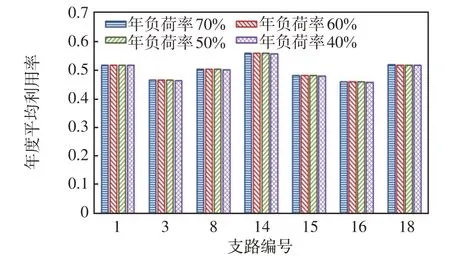
图7 情形3 中各支路的年度平均利用率变化情况Fig.7 Changes in annual average utilization of each branch in Case 3

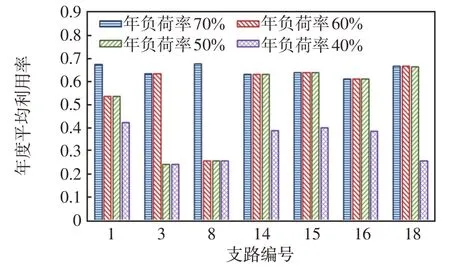
图8 情形1 中各支路的年度平均利用率变化情况Fig.8 Changes in annual average utilization of each branch in Case 1

从图6 中可以看出，负荷的尖峰特性对情形1的规划方案影响较大。当年负荷率从70%降低到40%时，情形1 的年综合费用增长较快（增长了8.37%），而情形2和情形3增长幅度不大（分别增长了0.23%和0.17%），情形3 相对情形1 的年综合费用降低比例也从16.82%提升到23.11%。可见，基于概率性时序生产模拟方法所得到的光储网协调规划方案对于负荷尖峰特性较明显的区域其经济性较好。

从图7 和图8 可以看出，随着年负荷率从70%降低到40%，情形3 基于概率性时序生产模拟方法得到的光储网规划方案能够充分利用分布式光伏的削峰能力和储能的移峰填谷能力，有效地平抑了负荷尖峰带来的影响，使得各支路运行平稳，且利用率始终保持在较高水平。而情形1 为了满足负荷尖峰的供电需求，只能不断地进行网架的升级改造，不仅使得建设工程量大幅上升，也造成各支路设备的利用率不断下降。可见，利用本文基于概率性时序生产模拟方法所得到的光储网协调规划方案对于负荷尖峰特性越明显的区域其优势更为显著。

4.2.3 光伏及储能单位成本对规划方案的影响

在进行光储网联合规划时，光伏与储能的成本将对规划方案产生较大的影响，因此在光伏成本3 600 元/kW、储能成本1 600 元/（kW·h）的基础上，本文对规划方案进行了光伏与储能单位成本的灵敏度分析，仿真结果如图9和图10所示。

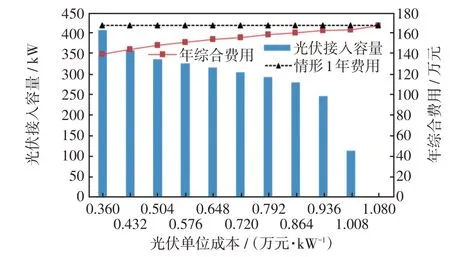
图9 光伏成本对规划方案的影响Fig.9 Impact of photovoltaic cost on planning scheme

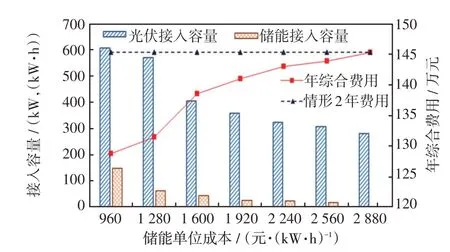
图10 储能成本对规划方案的影响Fig.10 Impact of energy storage cost on planning scheme

从图9 可以看出，随着光伏单位成本的上涨，光伏接入容量有所减少，系统年综合费用逐渐升高。当光伏单位成本达到10 800 元/kW，即基础价的3 倍时，系统自动寻优得到的规划方案与情形1吻合，即只进行网架的升级改造，不考虑光伏的接入，说明当光伏单位成本达到10 800 元/kW 以上时，配电系统规划考虑光伏已不具备经济效益。

从图10 可以看出，随着储能单位成本的上涨，光伏与储能的接入容量均呈下降趋势。当储能单位成本达到2 880元/（kW·h），即基础价的1.8倍时，系统自动寻优得到的规划方案与情形2吻合，即只考虑光伏与配电网架的联合规划，不考虑储能的接入，说明当储能单位成本达到2 880元/（kW·h）以上时，配电系统规划考虑储能已不具备经济效益。

5 结 论

本文针对负荷与分布式光伏出力的不确定性，提出了一种基于源荷概率性时序生产模拟的光储网协调规划方法。首先通过历史数据构建源荷概率性时序序列模型，利用生产模拟技术求取配电系统年运行概率状态；同时综合考虑光伏、储能、配电网的投资与运行损耗、停电损失、弃光损失及向上级电网的购电成本，建立基于随机优化的综合协调规划模型，通过投资决策与运行模拟两阶段的迭代寻优获得能够适应不确定因素的最优规划方案。算例仿真结果表明：

（1）基于源荷概率性时序生产模拟的光储网协调规划方法可以有效应对负荷与分布式光伏出力的不确定性，相对传统基于最大负荷运行断面的规划方法，本文方法得到的规划方案有利于源荷特性在长周期时序中的优化匹配，可以使得配电网的建设成本和运行成本都得到大幅度的降低，同时在提升设备利用率方面也具有一定优势。

（2）对于负荷尖峰特性较为明显的区域，利用本文基于概率性时序生产模拟方法所得到的光储网协调规划方案可有效降低配电系统的建设运行成本。尖峰特性越明显，利用本文方法进行光储网联合规划的优势越显著。

（3）光伏与储能的单位成本对光储网的规划方案影响较大。随着光伏与储能单位成本的上涨，光伏与储能的接入容量均呈下降趋势，系统年综合费用逐渐升高。光伏与储能的单位成本存在经济临界值，当超过其临界值时，配电系统规划考虑光伏与储能已不具备经济效益。