直驱风电场经MMC-HVDC 并网送端系统稳定性分析及振荡抑制

曾 瑞，雷 鸣，王一振，何晋伟

（天津大学智能电网教育部重点实验室，天津 300072）

在“双碳”战略目标和“十四五”发展规划的推动下，作为可再生能源的风电得到了快速发展。我国风能富集地带主要位于“三北”地区及深远海区域。基于模块化多电平换流器MMC（modular multilevel converter）的高压柔性直流输电HVDC（high voltage direct current transmission）技术具有输电损耗低、谐波含量小、可直接连接无源网络等优点，因此被广泛应用于远距离大容量风电外送[1-3]。

风电场经MMC-HVDC并网系统的电力电子化程度高，受电力电子设备交互作用等因素影响，送端系统易发生宽频振荡现象。例如：2013年德国北海Borwin1 系统在投入多个风场后，出现200～350 Hz左右的谐波振荡现象；2020年，张北四端柔直工程的张北站与米家沟双馈风场投入使用后，系统多次出现次同步振荡现象。因此，针对风电场经MMC-HVDC 并网系统的稳定性问题展开研究，并揭示其振荡失稳机理，提出相应振荡抑制策略，对保障大型风电基地外送系统的安全稳定运行具有重要意义[4-6]。

目前主要基于时域特征值法和频域阻抗法对风电柔直系统进行小扰动稳定性分析[7-8]。特征值法对系统整体进行小扰动线性化建模，通过状态矩阵特征值对系统进行稳定性分析。进一步，可基于参与因子分析得出系统振荡主导因素，但在系统规模较大时，建模过程易出现“维数灾”问题。阻抗法主要包含dq阻抗法及序阻抗法，两种分析方法本质上等价，可进行相互转换[9]。由于电力系统控制器通常基于dq同步旋转坐标系进行设计，因此基于dq阻抗法对系统进行稳定性分析更有利于指导实际设备的控制器参数设计及优化。

基于特征值法及时域仿真，文献[10]分析了直驱风场在不同锁相环控制参数情况下，功率变化对其稳定性影响，结果发现锁相环比例系数存在临界值，当锁相环比例系数大于临界值时，主导振荡模式阻尼与风场出力呈现负相关；当锁相环比例系数小于临界值时，主导振荡模式阻尼与风场出力呈现正相关。基于阻抗法及时域仿真，文献[11]对并网逆变器稳定性进行了分析，指出锁相环参数、系统功率及电网连接强度对系统阻抗及稳定性有很大影响；同时qq阻尼通道呈负电阻特性为导致系统振荡失稳主要原因。文献[12]对风电柔直系统稳定性进行分析，研究了锁相环带宽、MMC 交流电压控制参数对其稳定性影响，并提出虚拟并联阻抗控制策略，以进一步提升系统稳定性。

为对风电柔直系统振荡进行抑制，相关文献主要从系统参数优化、附加阻尼控制及增加滤波装置三方面展开研究。文献[13]基于谐波状态空间建立了MMC及风电场交流侧序阻抗模型，分析得出系统振荡失稳的重要原因是MMC特定频段下存在阻抗谐振峰以及风电场等效阻抗随功率增大逐渐减小，并进一步根据阻抗随系统参数变化趋势优化了MMC交流电压控制参数，实现了系统稳定性提升。文献[14]基于非支配排序遗传算法优化了风电柔直系统全局控制器参数，使系统特征值进一步向负半平面移动，降低了系统振荡失稳风险。但是，面对大规模风电并网变流器接入场景，相关控制器参数优化难度将显著增大。文献[15]研究发现，直驱风机并网变流器直流电压控制参数的不合理设置将使变流器端口交流阻抗出现谐振峰，进而引发一种中频振荡现象；为对此种振荡进行抑制，又进一步提出在MMC 交流电压控制环节附加虚拟电抗的控制策略，提升了系统的相角稳定裕度。针对双馈风电机组弱电网连接情况下的振荡失稳问题，文献[16]设计了一种新型对称锁相环结构，通过阻尼重塑增加了系统稳定裕度。然而，附加阻尼控制器通常针对系统特定频段进行阻尼重塑，可能降低系统在其他频段的阻尼特性。文献[17]设计了C 型滤波器，将其并联于MMC交流出口侧，并进一步通过附加控制回路提升了MMC的交流等效阻抗，但该方法增加了设备成本及占地面积，实际应用存在一定局限性。

本文首先以单元模块化形式建立了直驱风电场经MMC-HVDC并网送端系统的小扰动线性化模型，分析了风场有功变化对系统稳定性的影响。然后，建立了MMC 及风电并网变流器交流侧dq阻抗模型，从阻抗角度揭示了送端系统振荡失稳机理。进一步，提出了基于MMC交流电压控制外环q轴附加阻尼的振荡抑制策略。此策略相关计算量小，控制器复杂程度较低，仅在影响系统稳定性的关键环节发生作用，实际应用较为简便，且可满足系统满功率范围内的运行稳定性要求。最后，通过时域仿真验证了所提振荡抑制策略的有效性。

1 送端系统小扰动线性化模型

直驱风电场经MMC-HVDC并网系统结构如图1所示。图1（a）中，直驱风电场由多台风机构成，风机通过机端变压器进行升压汇流，汇流变压器将其进一步升压后接入送端MMC。送端MMC采取定交流电压控制策略，主要为风场提供稳定电压频率支撑。受端MMC 主要负责维持直流母线电压恒定，通常采取定直流电压/无功功率控制策略。

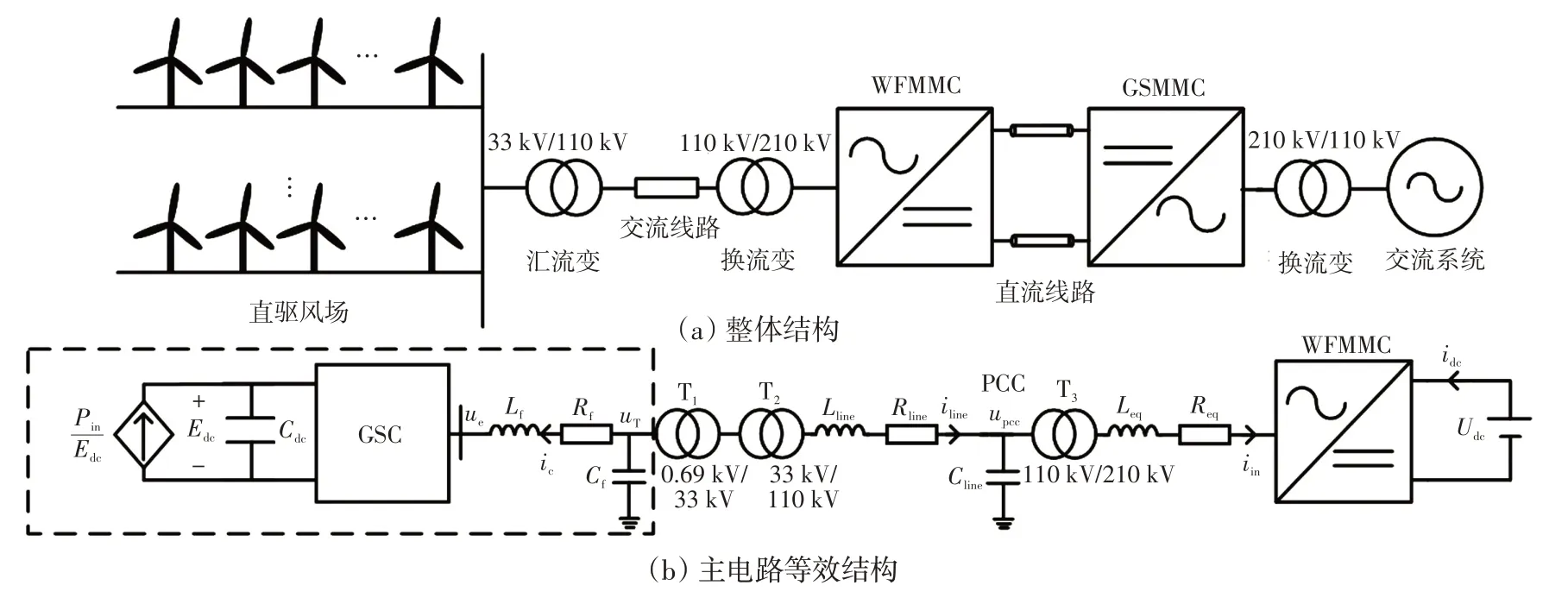
图1 直驱风电场经MMC-HVDC 并网系统结构Fig.1 Structure of direct-drive wind farm integration system via MMC-HVDC

在研究直驱风电场经MMC-HVDC并网系统稳定性时，本文关注重点为风电场与送端MMC 互联部分。直驱风电场由于直流稳压电容解耦作用，可将机侧部分等效为电流源[18]，进一步通过改变电流源电流大小来模拟风速及有功变化。由于受端MMC 采取定直流电压控制策略，因此可将其等效为直流电压源[19]。简化系统主电路等效结构如图1（b）所示，其中直驱风电场采用单机聚合模型进行等值[10]，其风场额定容量为600 MW，由300 台单机容量为2 MW的风电机组等效聚合而成。图中：Pin为风场输出有功，ue为风机阀侧出口交流电压，ic为风机出口交流电流，uT为滤波电容电压，iline为交流线路电流，upcc为并网点PCC 处交流电压，Leq和Req为MMC 交流侧等效电感和电阻，im为MMC出口交流电流，idc为WFMMC直流侧电流。系统其他参数如表1所示。

表1 系统参数Tab.1 Parameters of system

1.1 送端MMC 动态模型

送端MMC 包含主电路及控制系统两部分，需分别建立其动态特性方程。MMC 的主电路模型在文献[19]中已有阐述。需要说明的是，在针对MMC电容电压波动及环流间耦合关系进行建模时，由于高次环流引起的电容电压波动很小，本文仅考虑电容电压波动的基频分量和二倍频分量。

送端MMC 控制系统包括交流电压控制、交流电流控制和环流控制，如图2 所示，其中送端MMC交流电压控制策略如图2 中虚线方框部分所示。图中：upccdref和upccqref为交流电压参考值upccref的d、q轴分量；upccd和upccq为交流电压测量值的d、q轴分量；imdref和imqref为交流电流参考值的d、q轴分量；imd和imq为交流电流测量值的d、q轴分量；ed和eq为MMC 阀侧调制输出电压的d、q轴分量，各dq轴分量均基于基频同步旋转坐标系进行abc-dq坐标变换而得到；G1与G2分别表示交流电压环、交流电流环的PI 控制器；ω0为固定旋转角频率，ω0=100π；Leq=Larm/2，Req=Rarm/2，Larm和Rarm为MMC桥臂电感和电阻。

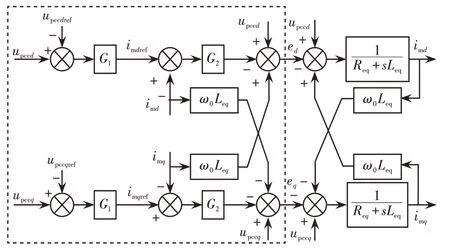
图2 MMC 交流电压控制框图Fig.2 Block diagram of AC voltage control of MMC

根据图2 列写交流电压控制环的动态特性方程，即

式中，z1～z4为定义的状态变量，对应G1、G2中积分器所存储的历史数值。

为降低子模块电容电压波动及MMC 内部损耗，通常采取环流抑制策略对MMC 内部二倍频环流进行抑制。MMC环流控制策略框图如图3所示，其中：icirdref和icirqref为环流电流参考值的d、q分量；icird和icirq为环流电流测量值的d、q分量；G3为环流PI 控制环节；vcird和vcirq为环流调制电压的d、q分量。需要说明的是，环流控制中各dq轴分量均基于二倍频同步旋转坐标系进行abc-dq坐标变换而得到。二倍频同步旋转角为基频同步旋转角的2倍。

图3 MMC 环流控制框图Fig.3 Block diagram of circulating current control of MMC

根据图3 对MMC 环流控制部分列写动态特性方程，即

式中，z5、z6为定义的状态变量，对应G3中积分器所存储的历史数值。

MMC 主电路部分与控制系统部分通过输入输出量相互耦合联系，将各输入输出量联立即可得MMC单元模块化动态模型。

1.2 直驱风电场动态模型

直驱风电场同样包含主电路及控制系统两部分，需分别建立其动态特性方程。直驱风电场主电路结构如图1（b）中虚线方框部分所示，包含直流电路部分、变流器部分及交流出口滤波器部分。变流器出口采用LC 型滤波器，滤除网侧变流器输出的高次谐波。文献[10]详细建立了直驱风电场主电路部分动态特性方程，本文不再赘述。

直驱风电场网侧变流器采取定直流电压/无功功率控制策略，其控制策略如图4 中方框部分所示。其中：Edcref和Edc分别为直流电压参考值和实际值；和分别为交流电流参考值的d、q轴分量；和为交流电流测量值的d、q轴分量；和为交流电压测量值的d、q轴分量；G4和G5分别为直流电压环、交流电流环的PI 控制器；和为风机阀侧出口电压d、q轴分量测量值，上标c表示相关d、q轴分量均基于直驱风电场并网口电压的同步旋转坐标系进行abc-dq坐标变换得到的；uTd和uTq为主电路交流电压d、q轴分量实际值；icd和icq为主电路交流电流d、q轴分量实际值；ued和ueq为风机阀侧出口电压d、q轴分量实际值。

图4 PMSG 网侧变流器控制框图Fig.4 Control block diagram of PMSG grid-side converter

根据图4，对直驱风电场控制系统部分列写动态特性方程，即

式中，z7～z9为定义的状态变量，对应G4、G5中积分器所存储的历史数值。

直驱风电场网侧变流器锁相环部分控制策略如图5 所示。图中：uTa、uTb、uTc为uT三相电压；Gpll代表锁相环PI控制器；kppll、kipll为PI控制器比例、积分系数。根据图5，对锁相环部分列写动态特性方程，即

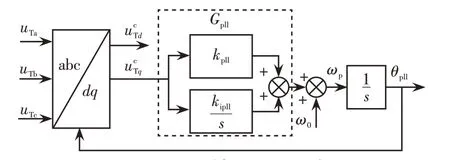
图5 PMSG 锁相环控制框图Fig.5 Block diagram of PLL control of PMSG

式中：z10为定义的状态变量，对应锁相环积分器所存储的历史数值；θpll为锁相环输出相位；ωp为锁相环角频率。

直驱风电场主电路与控制系统通过输入输出量相互耦合联系，将各输入输出量联立即可得直驱风电场单元模块化动态模型。

1.3 送端系统小扰动模型及时域仿真验证

送端系统中直驱风电场与MMC分别基于不同旋转坐标系进行矢量控制，为在统一旋转坐标系下对系统进行稳定性分析，需进行坐标变换。

系统中三组坐标系如图6 所示，其中DQ为MMC 本地旋转坐标系，dq与dcqc分别为直驱风电场本地主电路旋转坐标系及控制系统旋转坐标系。MMC 本地DQ旋转坐标系以恒定角频率ω0进行旋转，直驱风电场本地主电路旋转坐标系同样以恒定角频率ω0进行旋转，但由于线路阻抗及功率传输影响，其与MMC 本地旋转坐标系角度相差功率角θ0，而θ0需基于潮流方程及初值求解程序进行求解。dcqc为风电机组控制系统本地旋转坐标系，在系统出现扰动时其将与主电路旋转坐标系产生角度偏差Δθpll。

图6 坐标变换框图Fig.6 Block diagram of coordinate transformation

根据图6 可得直驱风电场控制系统与主电路之间变量，主电路与MMC 之间变量的坐标转换关系为

式中：Δ 代表扰动量；y代表相关变量；下标d、q及D、Q代表dq坐标系及DQ坐标系下变量；下标0 代表相关变量稳态初值；上标c 代表风机控制系统下相关变量。

以MMC 本地旋转坐标系为基准，在统一旋转坐标系下联立直驱风电场、送端交流输电线路及MMC 的动态特性方程，并进行小扰动线性化。可得送端系统整体小扰动线性化状态空间方程为

式中：A、B为系数矩阵；X和U为系统所有状态变量和所有输入变量所组成的矩阵，分别表示为

式中：ucdc、uc1d、uc1q、uc2d、uc2q为MMC 平均电容电压的直流分量、基频的d、q轴分量和二倍频的d、q轴分量；idc为MMC直流侧电流（流入为正）；ilined、ilineq为传输线路交流电流d、q轴分量。

依据上述分析及表1 参数，在Matlab 软件中建立系统小扰动线性化时域常微分方程模型，同时在PSCAD中建立系统时域电磁暂态仿真模型，将二者相应电气量的动态响应波形进行对比，如图7 所示。风电柔直系统初始阶段稳定运行，风场输出有功功率为200 MW。10 s 时使风场有功小幅阶跃上升30 MW，送端MMC 直流电流idc，风电机组直流电压Edc的PSCAD 时域仿真波形与Matlab 小扰动线性化模型响应波形对比如图7所示。由图可见，PSCAD 时域仿真结果与Matlab 小扰动线性化模型响应结果具有很好的一致性，验证了所建立小扰动线性化模型的正确性。

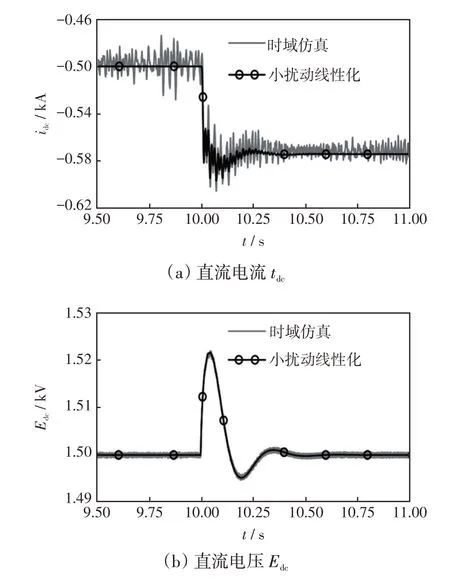
图7 功率阶跃响应波形对比Fig.7 Comparison of response waveforms under step change in power

2 送端系统振荡模式分析

2.1 功率运行点对送端系统稳定性影响

基于第1 节所建立的小扰动线性化模型，对送端系统稳定性受功率运行点影响规律进行研究。使系统功率从0 均匀变化至490 MW，系统特征值变化情况如图8所示，图中仅展示了离虚轴较近的4 对振荡模式，其他远离虚轴的振荡模式对系统稳定性无显著影响。由图8中可见，模式1、模式2、模式3 特征值受系统功率变化影响较大，其中模式1为系统主导振荡模式，其特征值随有功功率增大逐渐向右半平面移动，直至系统振荡失稳；同时可以看出，特征值轨迹在右半平面分布趋于水平方向，表明功率主要影响模式1的阻尼特性，对振荡频率的影响较小，且其频率均处于低频振荡的频率范围。

图8 系统特征值随有功功率变化轨迹Fig.8 Root locus of system eigenvalues under different values of Pwind

为探究影响互联系统稳定性的主要因素，分析了参与因子，得到参与因子分布图谱，如图9 所示。系统共30 个状态变量，状态变量编号与式（8）中顺序完全相同。由图9可见，送端系统稳定性主要受MMC 交流电压控制环及风电机组锁相环影响；得益于环流抑制对MMC内部稳定性的提升，互联系统稳定性几乎不受MMC内部动态的影响。

图9 参与因子Fig.9 Participation factor

2.2 时域仿真验证

首先，使系统稳定运行于440 MW，在10 s时使系统有功小幅阶跃上升至465 MW，则并网点PCC处系统有功功率PPCC波形及对应的频谱分析如图10所示。由理论计算可知，系统临界失稳功率为460 MW，此时模式1 特征值为0.82±j84.18，对应振荡频率为13.39 Hz。由图10 可见，有功阶跃上升至465 MW后，系统逐渐振荡失稳，且振荡频率为13.30 Hz，与特征值分析法所得振荡频率13.39 Hz 基本一致。以上从系统临界失稳功率及振荡频率角度均验证了基于特征值变化轨迹进行系统稳定性分析的有效性。

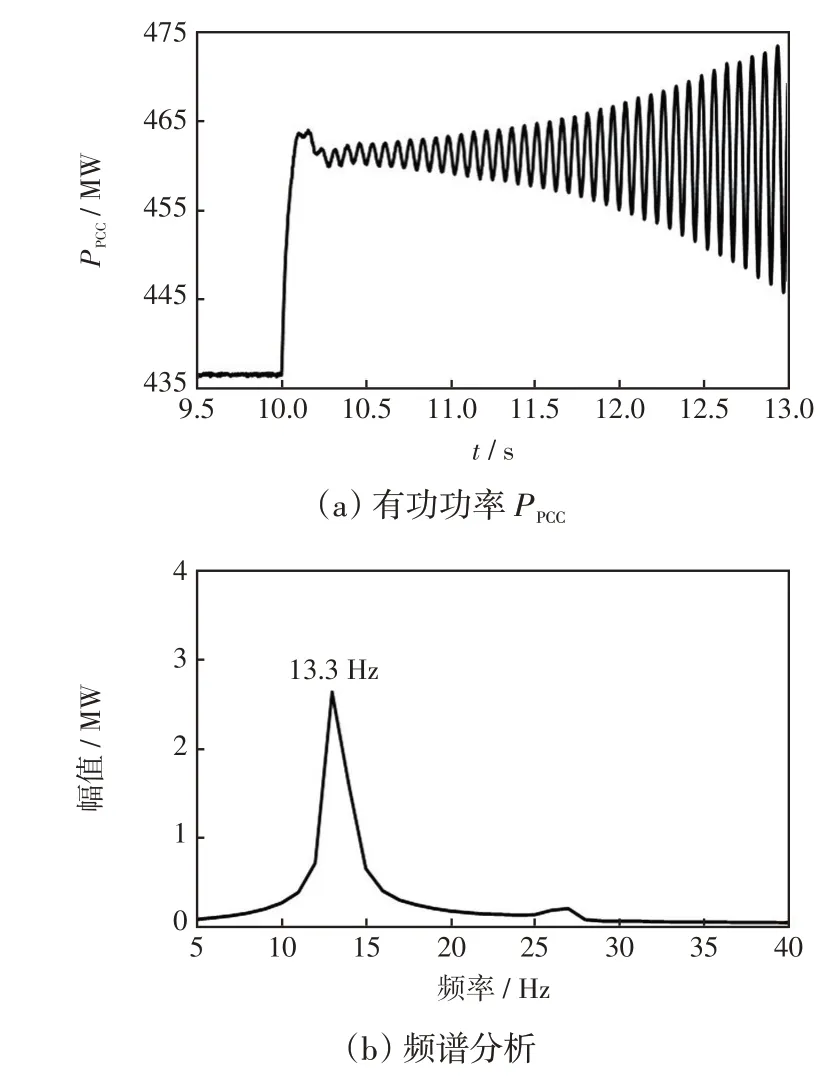
图10 有功小幅阶跃后PCC 有功功率曲线Fig.10 Active power curve at PCC after small step up of active power

3 系统阻抗建模及振荡机理揭示

本节从阻抗角度揭示送端系统振荡机理，并提出相应振荡抑制策略。由图9可知，在MMC环流抑制投入的情况下，互联系统稳定性受MMC 内部动态的影响极小，因此在求解送端系统阻抗时可忽略MMC 内部动态。此外，风电机组滤波电容及输电线路对地电容对系统低频段稳定性影响极小，阻抗建模时同样可以忽略[18]。

3.1 MMC 交流侧小信号dq 阻抗

根据图2 进行分析，可建立MMC 交流电流、交流电压的控制环小信号模型为

由于MMC 输出电压波形在低频段的精度很高，此处忽略调制误差。

进一步，建立MMC交流电路侧小信号模型为

联立式（10）～式（12），可求解得MMC交流侧小信号阻抗矩阵为

式中：上标MMC 表示MMC 的阻抗；下标dd、dq、qd、qq表示MMC 阻抗的dd、dq、qd、qq分量，下同，不再赘述。

同理，可求解得输电线路等效阻抗为

MMC 交流侧阻抗与输电线路阻抗串联，可得从MMC侧的等效总阻抗为

忽略非对角元素影响[20]，则有

3.2 直驱风机并网变流器交流侧dq 阻抗

根据图4 建立风机并网变流器直流电压及交流电流控制环的小信号模型为

基于功率守恒并忽略损耗，建立风机并网变流器直流电容电压的小信号模型为

此处已默认风机并网变流器处于单位功率因数运行状态。

风机并网变流器交流侧主电路小信号模型为

联立式（5）、式（17）～式（20），得风机并网变流器交流侧dq阻抗为

3.3 振荡机理揭示

基于前文所得MMC及风机并网变流器的交流侧阻抗，运用广义Nyquist 判据对系统稳定性进行分析[11]。互联系统稳定前提为广义矩阵η特征根的根轨迹不包围点（-1，0），其中η表示为

根据式（22），可求得矩阵η的2 个特征根：特征根1为，特征根2为

系统不同传输有功功率下矩阵η的两特征根轨迹如图11 所示。由图可见，不同有功功率下特征根1的根轨迹始终位于右半平面；而随系统有功增大特征根2的根轨迹逐渐趋向于包围点（-1，0），在有功功率为465 MW时特征根2的根轨迹包围点（-1，0），表明系统振荡失稳，此时特征根穿越频率为13.3 Hz。可以验证得出，特征根轨迹随系统有功变化趋势、系统临界失稳功率、振荡频率均与前文基于状态空间特征值法的分析结果基本一致。

图11 不同有功功率情况下特征根1、2 的根轨迹Fig.11 Root locus of eigenvalues 1 and 2 under different values of Pwind

由上述分析可见，互联系统稳定性主要受矩阵η的特征根2 影响，不同参数情况下特征根1 的根轨迹始终位于右半平面，远离点（-1，0）。下文主要围绕特征根2 展开分析，为便于讨论列写特征根2的具体表达式为

由式（23）可见，特征根2 与系统传输有功功率、MMC 交流电压控制参数及风机并网变流器锁相环参数密切相关，相关参数变化会对系统稳定性产生影响。不同有功功率情况下MMC 侧阻抗与风机并网变流器侧阻抗如图12所示，其中图12（a）为0～100 Hz 范围的阻抗，图12（b）为0～20 Hz范围的阻抗局部放大。

图12 不同有功功率下MMC 及风机并网变流器阻抗特性曲线Fig.12 Impedance characteristic curves of MMC and PMSG grid-connected converter under different active power conditions

由图12 可见，0～100 Hz 频段MMC 侧阻抗呈正阻感特性，且阻抗幅值及相位均不受系统有功变化影响；风机侧阻抗幅频曲线随系统有功功率增大而下移，相频曲线不受系统有功变化影响。具体而言，在0～40 Hz的低频段呈负阻容特性，在40～100 Hz 的频段呈正阻容特性。当有功功率增大到临界功率465 MW 时，阻抗幅频曲线与MMC侧阻抗幅频曲线相交，交点对应频率下的相角裕度不足0°以上，即系统满足发生低频振荡的条件。

4 振荡抑制及仿真验证

4.1 振荡抑制策略

根据图12 分析可知，为使不同有功情况下送端系统始终保持稳定，可采取2 种措施：一是使不同有功功率下阻抗与幅频曲线始终不相交，且阻抗幅频曲线始终位于阻抗幅频曲线之下；二是使不同有功功率下阻抗与幅频曲线相交时，对应频段下相角裕度始终大于0°。本文根据第1 种措施来设计阻尼控制器，以实现振荡抑制，具体策略如图13 中虚线方框部分所示，其添加于MMC交流电压控制外环q轴通道上。

图13 基于附加阻尼控制的振荡抑制策略框图Fig.13 Block diagram of oscillation suppression strategy based on additional damping control

图13 中，附加阻尼控制首先通过高通滤波器滤除imq中直流分量，防止正常运行时imq稳态直流量造成交流电压upccq参考值偏差，Rvir为虚拟电阻。依据图13重新计算为

进一步重新计算为

由式（25）可知，附加阻尼控制仅使多出一项-sRvir/(s+20)。满功率600 MW时，不同Rvir取值情况下系统阻抗如图14所示，其中图14（a）为0～100 Hz范围阻抗，图14（b）为0～30 Hz 范围阻抗局部放大。由图可见，随虚拟电阻Rvir增大，幅频曲线下移。当Rvir取值0.8 p.u.时，阻抗幅频曲线始终位于阻抗幅频曲线之下，二者不再相交，符合系统稳定性条件。

图14 附加阻尼控制后不同有功情况下MMC 及风机并网变流器阻抗特性曲线Fig.14 Impedance characteristic curves of MMC and PMSG grid-connected converter under different active power conditions after additional damping control

4.2 时域仿真验证

为验证所提基于附加阻尼的振荡抑制策略的有效性，基于表1 参数在Matlab 软件中搭建全比例仿真模型。首先使风场有功出力保持为440 MW，10 s时使风场有功阶跃上升至465 MW；14 s投入图13所示附加阻尼控制策略，其中Rvir取0.8 p.u.；14.5 s使风场有功阶跃上升至额定功率600 MW。并网点PCC 处系统有功功率PPCC及无功功率QPCC波形如图15 所示。由图可见，10 s时系统有功阶跃上升至465 MW后，系统开始出现振荡失稳现象，且振荡频率为13.39 Hz；14 s投入所提振荡抑制策略后，系统振荡消失且迅速恢复稳定；当14.5 s 系统有功阶跃上升至600 MW后，系统仍能稳定运行，且后续无振荡趋势。以上结果证明了本文所提基于附加阻尼的振荡抑制策略的有效性。

5 结 语

针对直驱风电场经MMC-HVDC并网送端系统小扰动稳定性问题，本文首先基于小扰动线性化模型和特征值法分析了风场有功出力对送端系统稳定性的影响。研究发现，随风场有功出力增大，系统稳定性逐渐降低，在一定参数条件下易发生振荡失稳。进一步，建立了送端系统dq阻抗模型，从阻抗角度揭示了送端系统振荡失稳的物理机理，即MMC 交流阻抗与风机并网变流器交流阻抗的幅频曲线相交，且交点对应频率下相角裕度不足0°以上。最后，提出了基于MMC交流电压控制外环q轴附加阻尼的振荡抑制策略。全比例模型时域仿真结果验证了理论分析及所提振荡抑制策略的有效性。