基于转子动能的双馈风机频率支撑优化方法

文立斌，胡 弘，孙志媛，卢广陵，吴健旭，窦 骞

（广西电网有限责任公司电力科学研究院，南宁 530023）

助力实现“碳达峰、碳中和”目标，需要推动新能源发展，安全稳步提高新能源发电量占全口径发电量的比例。风能作为一种在全世界分布广泛的可再生能源，风力发电已成为主要的新能源发电形式[1]。受制于自然环境，风力发电的间歇出力特性与系统负荷特性存在明显的时空差异，同时，随着电力系统电力电子化程度逐渐加深，风电机组取代传统同步发电机组的比例逐渐升高，交流系统的等效惯量与阻尼持续降低。在此背景下，系统频率安全问题凸显，成为了目前新型电力系统所面临的挑战[2-3]。

双馈风力发电机DFIG（doubly-fed induction generator）因单机容量大、变流器容量小、风能利用效率高、控制灵活且接入交流系统友好等优势，成为了主流风力发电机类型[4]。正常运行时，DFIG在机侧变流器解耦控制下工作于最大功率点跟踪MPPT（maximum power point tracking）模式，实现对风能的最大捕获；同时，网侧变流器将风机功率输送至交流电网，并向电网提供无功功率与电压支撑。然而，运行于MPPT典型控制架构下的DFIG将风机转子转速与交流系统频率相解耦，使DFIG 不能以传统同步发电机的方式参与频率调节。为此，有研究提出，通过虚拟惯量综合控制释放转子动能、或通过桨距角控制、超速减载等策略实现风电机组对交流系统频率的支撑[5-7]，其中：虚拟惯量综合控制响应迅速，可提供惯量阻尼，但持续时间短，存在二次频降；桨距角控制功率平稳，适用于全风况，但响应较慢，经济性较低；超速减载控制响应较快，适用于功率备用，经济性较低，不适合高风速。

在DFIG 虚拟惯量综合控制中，由于受到转子转速的安全约束以及调频的能量限制，当DFIG 停止参与频率调节并进行转速恢复时，交流系统还将出现频率的二次跌落问题[8]。为此，文献[9]提出附加风机转速微分反馈环节的方法、综合风速及转速自适应改变下垂控制系数的方法，以降低转速恢复速度，并避免因DFIG 退出调频而引发的功率冲击及频率波动问题；文献[10]则基于模糊协同控制，提出修正DFIG 转速控制器参数，缓解风机固有控制结构与调频环节间矛盾的参数匹配策略。为满足风电并网要求，风电机组本应具备适当的调频能力。因此，文献[11-12]在保留DFIG 传统虚拟惯量控制的基础上，融合变桨距控制或超速减载策略，使得DFIG 在最大限度保留转子动能的同时，也具有充足的备用调频功率，从而保证了风电机组的辅助调频功能，但减载运行也让DFIG 无法在正常运行时工作于MPPT 模式，牺牲了风电机组的运行经济性。此外，区别于传统集中式控制架构，文献[13]基于分布式牛顿法实现了全风场DFIG转子动能的改进优化控制，提高了风机参与频率调节的可靠性。区别于传统DFIG的虚拟惯量控制，文献[14]利用柔性变流器的灵活可塑性，将风机输出功率曲线作为决策变量，设计最优风机调频功率曲线，充分抬高了功率扰动下的频率最低点，并解决了频率二次跌落问题。

综上，目前研究的重点在于如何避免频率二次跌落问题。然而，频率二次跌落问题并不是不可接受的，系统频率面临的最主要的矛盾是如何提高频率最低点以减少低频减载量，减少对系统产生的非必要影响。因此，本文提出基于转子动能的DFIG频率支撑优化方法，主要创新工作如下。

（1）在DFIG 通过转子动能控制参与调频的基础上，分阶段建立系统频率最低点的优化函数，得到DFIG在附加惯量阻尼控制中改善暂态频率特性的最优控制参数。

（2）所提DFIG 频率支撑优化方法实现了多运行工况下转子动能的优化控制，最大程度抬升了功率扰动下的频率最低点，防范了低频减载风险并提高了频率安全稳定性。

1 MPPT 及调频控制架构

风电机组的输出功率表达式为

式中：PWm为风电机组捕获的功率，即输出机械功率；ρ为空气密度；R为风轮半径；vW为风速；λ为叶尖速比，λ=ωmR/vW，其中ωm表示风轮转速；β为桨距角；Cp(λ,β)为风能利用系数，表达式为

式中，λ1为关于λ和β的中间变量。基于式（2），绘制Cp在不同β下随λ变化时的曲线，如图1所示。

当β=0 时，存在最佳叶尖速比λopt，使得风电机组始终能保持在充分利用风能的最佳状态，通过反馈控制ωm随风速vW发生改变可实现对风电机组的MPPT控制。在DFIG的典型控制架构中，通过控制机侧变流器输出电流的大小及频率，调整感应发电机的转子运行状态，可实现DFIG 对风能的最大捕获。运行于MPPT 下的DFIG 在交流系统中可等效为恒功率源，也可视为零惯量的同步发电机，随着风电机组替代传统同步发电机的比例逐渐升高，交流系统等效惯量及等效阻尼将会大幅降低，严重危害交流系统的安全可靠运行。

在传统交流系统中，同步发电机通过感知交流系统频率偏差，自适应释放或吸收转子动能参与系统惯量支持。DFIG转子运行状态虽与系统频率相解耦，但当DFIG 输出电磁功率与输入机械功率不平衡时，风机转子转速也将依据功率平衡情况发生改变。

含频率支撑的DFIG功率控制模块如图2所示，图中：调频控制参数KD表示惯量系数，KP表示阻尼系数；f与Δf分别为交流系统频率及其相对于额定值的偏差；为DFIG频率支撑控制的输出功率指令。通过在DFIG控制架构中增加额外的频率支撑模块，DFIG 将通过临时释放风机转子动能向交流系统提供频率支持，实现类似同步发电机参与一次调频的效果。当交流系统出现频率偏差后，通过频率支撑控制改变DFIG机侧变流器的功率指令，即可调整DFIG 转速并使其参与频率调节。当风机调频过程结束后，转子转速下降，运行状态偏离MPPT 最优状态，可增加转速恢复控制使扰动后风机工作模式恢复到MPPT。

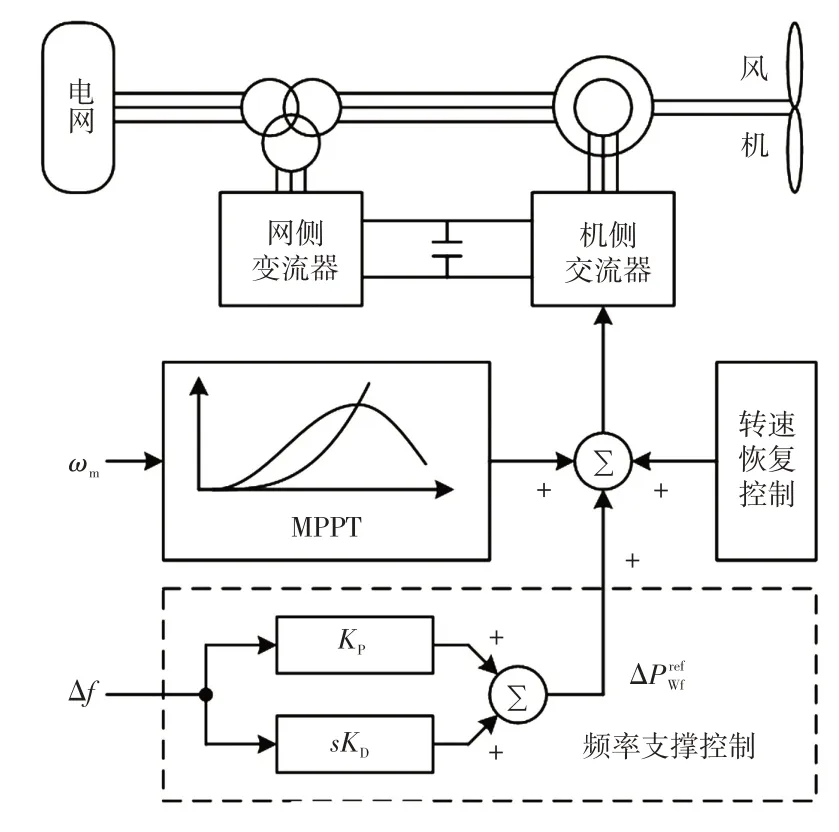
图2 含频率支撑的DFIG 功率控制模块Fig.2 Power control module of DFIG including frequency regulation

2 基于DFIG 转子动能优化控制的频率支撑策略与参数设计方法

2.1 含DFIG 接入的频率动态

本文以发电机、DFIG 或系统额定容量为基值对各设备电气量标幺化，规定电流与功率的正方向为注入交流系统方向。在新型电力系统中，设DFIG 装机容量占系统总容量的比例为R，且所有DFIG 均配置如图2 所示的调频模块。根据同步发电机摇摆方程得交流系统频率响应的框图，如图3所示。

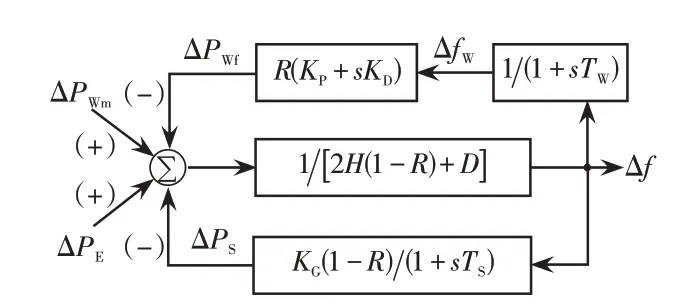
图3 频率动态响应框图Fig.3 Block diagram of dynamic response of frequency

交流系统频率的动态方程表达式为

式中：Δfw为频率f的中间变量；H为同步发电机的惯性时间常数；ΔPE为扰动功率；ΔPS为同步发电机参与调频后额外输出的电磁功率；D为负荷频率调节效应系数；ΔPWf为DFIG额外输出的调频功率；ΔPWm为因DFIG转子转速变化导致的风机输出机械功率的改变量。同步发电机和风机调频功率ΔPS、ΔPWf的传递函数分别表示为

式中：KG为发电机组的单位调节功率；TS为发电机的原动机-调速器系统的等效时间常数；TW为DFIG的输出功率指令-实际输出功率控制环节的等效时间常数。

在式（1）的基础上，设桨距角β=0 且风速恒定不变，则式（3）中ΔPWm表示为

式中，下标0表示0时刻变量的初始值。此外，DFIG风轮转速的动态方程为

式中，JW为DFIG转子的转动惯量。

如图1 所示，若风速恒定且转速变化不大，则DFIG 输出机械功率变化也不大。若忽略ΔPWm对系统频率的影响，则原有非线性系统转化为线性系统，由式（3）～式（5）得系统状态空间为

由于DFIG 控制时间常数TW远小于同步机的原动机-调速器时间常数TS，故可继续忽略TW对频率动态的影响，得到频率偏差Δf关于扰动功率ΔPE的传递函数为

式中，Jeq、Deq、Keq分别为DFIG 参与频率调节后交流系统的等效惯量、等效阻尼与等效单位调节功率。式（9）说明，风机调频后交流系统的等效惯量与阻尼得到了增强。然而，受到风电机组转子转速与风能利用系数Cp的限制，DFIG 参与调频的能量有限，交流系统并不能长时间维持在Jeq、Deq这些惯量及阻尼增强后的状态，调频控制参数KD与KP的优化还需考虑二次频降问题。

2.2 调频控制参数的优化设计

以上表达式说明：新能源占比(R)、同步发电机组参数(KG,H,TS)、风电机组参数(Kp,KD,JW,TW)、负荷频率调节效应系数(D)的变化均会对频率动态产生影响。因此，当系统参数R、KG、H、TS、JW、TW、D均已得到确定后，以式（1）～式（7）为约束方程，即可通过优选控制参数KD与KP促使频率偏差在功率扰动ΔPE发生后最小。

DFIG正常运行时的转速约为0.7～1.3 p.u.。从0时刻DFIG 开始释放转子动能后，转子转速随之持续降低，直至TC时刻风轮转速达到最低限值(ωm=ωmin)，ωmin为风轮转速最低限值，此时风机不再向交流系统提供频率支持，同时风机所捕获的风能也因ωm降低而减小。故有

式中，下标0表示0时刻变量的初始值。

在失去DFIG 的频率支撑后，交流系统频率将出现二次跌落，此频率跌落所导致出现的频率最低点，存在小于扰动后首次出现的频率最低点的可能，因此，频率二次跌落问题增加了系统低频减载风险，给系统运行带来了安全隐患，必须着重考虑此问题并将其对频率最低点的影响降至最小。

综上，针对DFIG是否参与调频，将频率动态过程划分为DFIG 参与调频时与完成调频后两个阶段，则调频控制参数KD与KP的优选转化为规划问题，即

式中，F为优化目标。

当频率偏差最小化后，交流系统频率在功率扰动下的频率最低点将被最大化，从而通过调整DFIG的调频控制模块参数实现充分降低系统低频减载风险的目标。在系统发生功率扰动后，同步发电机将在自动发电控制AGC（automatic generation control）的作用下，调整电网稳态频率至额定值附近，同时在所述DFIG 频率支撑控制策略下，DFIG的工作点也将重新恢复至MPPT。

3 算例分析

3.1 控制参数的整定

系统选定基本参数如表1 所示，在此基础上讨论所述控制参数优化设计的具体应用，得到满足最小频率偏差的最优KD与KP选值。

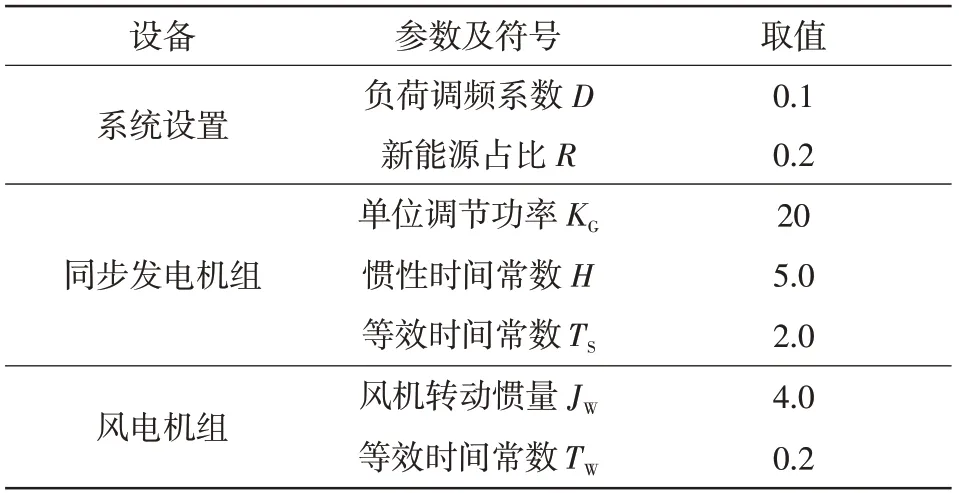
表1 系统基本参数设置Tab.1 Setting of basic parameters of system

功率扰动越大，频率偏差也越大，故调频参数KD与KP的整定应该在具有较大功率扰动的条件下进行。在环境风速vW等于风机额定风速vWn、稳态下DFIG 处于MPPT 模式、功率扰动ΔPE=-0.2的工况下绘制频率偏差关于DFIG 调频控制参数KD与KP的变化情况如图4 所示。据此，存在多种参数取值均可从最大程度上抬高频率最低点，如图4 中黑点所示，当KD=10.5、KP=17 时，频率偏差缩小至-0.965 Hz，而频率最低点将提高至49.035 Hz。

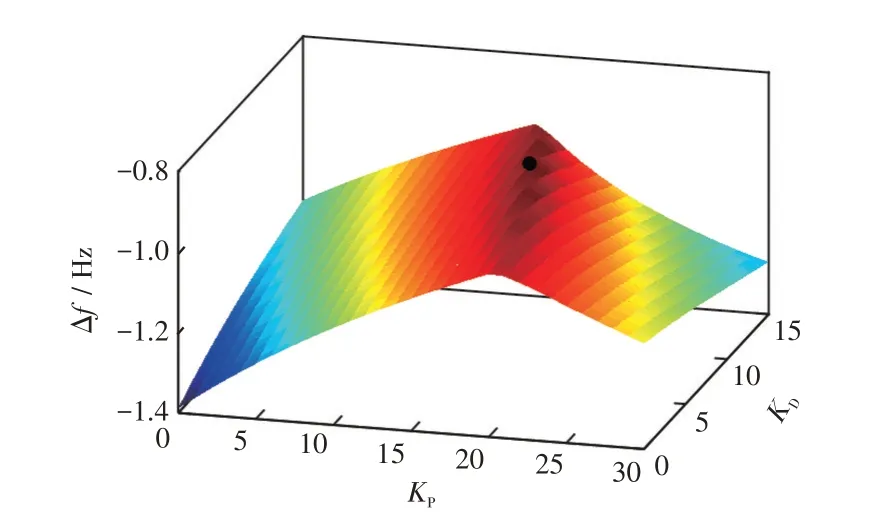
图4 频率偏差关于KD 与KP 的变化情况Fig.4 Frequency deviation with different values of KD and KP

3.2 仿真验证

本文在ADPSS 平台中搭建详细仿真模型。基于KD=10.5、KP=17 时的DFIG 调频控制参数，在额定风速下，得到t=5 s 时系统发生ΔPE=-0.2 扰动工况下交流系统的频率、DFIG 转速及其输出机械功率波形，如图5所示。系统发生ΔPE=-0.15 扰动工况下交流系统的频率波形如图6所示。

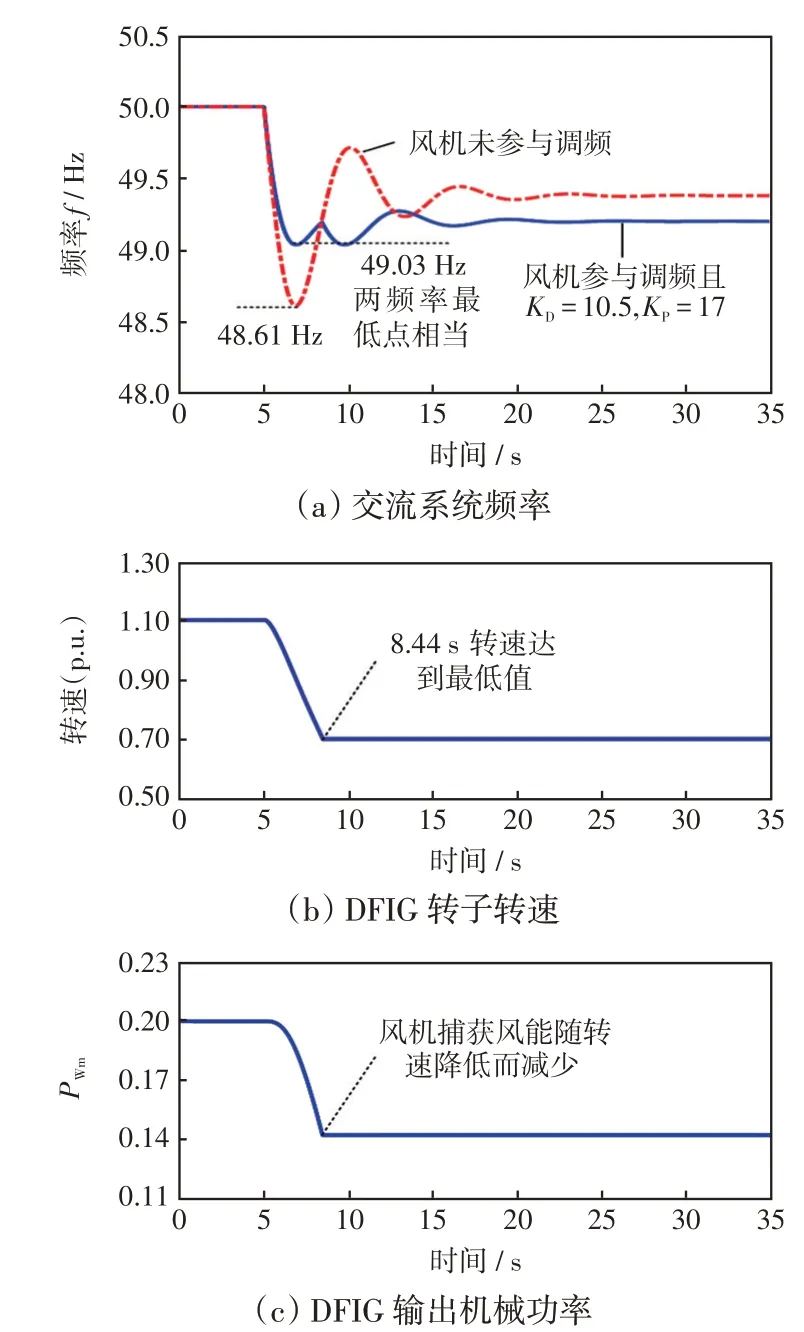
图5 当DFIG 调频参数KD=10.5、KP=17 时系统在ΔPE=-0.2 扰动下的仿真波形Fig.5 Simulation results with the regulation of DFIG when KD=10.5,KP=17 and ΔPE= -0.2

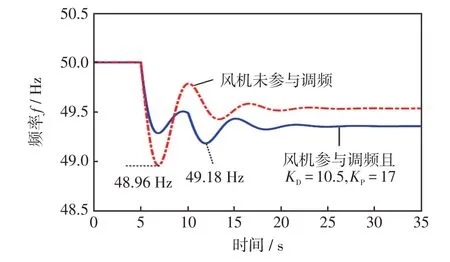
图6 当DFIG 调频参数KD=10.5、KP=17 时系统在ΔPE=-0.15 扰动下的频率波形Fig.6 Frequency waveforms with the regulation of DFIG when KD=10.5,KP=17 and ΔPE=-0.15

由图5（a）频率波形可见，相较于风电机组不参与调频的情况，DFIG 启用基于转子动能优化控制参与频率支持后，在最优调频参数设计指导下，频率最低点大幅拉升，由48.61 Hz抬升至49.03 Hz，频率偏差减少约30%。如图5（b）转子转速波形所示，在DFIG 于8.44 s 完成转子动能释放后，DFIG 停止向交流系统提供功率支撑ΔPWf，此时，系统频率出现二次跌落，频率二次跌落与频率首次跌落具备相当的频率最低点，且频率的波动幅值更小、动态过程更平滑。此外，由图5（c）功率波形可见，因DFIG参与调频后的转子转速下降，其输出功率不再等于初始最大输出功率，从而造成图5（a）中稳态频率偏差略大于风电机组不参与调频时的偏差值。通过AGC 和转子转速恢复控制，DFIG 可在电网频率恢复的过程中重新工作于MPPT模式。

基于上述参数优化设计方法，不同扰动功率下整定的调频控制参数KD与Kp不尽相同，但在实际|ΔPE|小于整定值下，系统频率偏差仍可控制在安全范围以内。

由图6 可见，在ΔPE=-0.15 的扰动工况下，DFIG 参与调频且KD=10.5，KP=17 时，频率二次跌落下的频率偏差将大于频率首次跌落下的频率偏差，这导致频率最低点达到49.18 Hz，略低于基于ΔPE=-0.15 重新优化下的频率最低点49.20 Hz。但是，相较于风机未参与调频的情况，此时的最大频率偏差仍然缩小了约21%，仍起到充分降低系统频率运行安全风险的作用。

在扰动ΔPE=-0.2 及额定风速工况下，分别设计2 组非最优调频控制参数：KD=10.5、KP=10；KD=10.5、KP=25，并基于此得到频率仿真波形如图7所示。

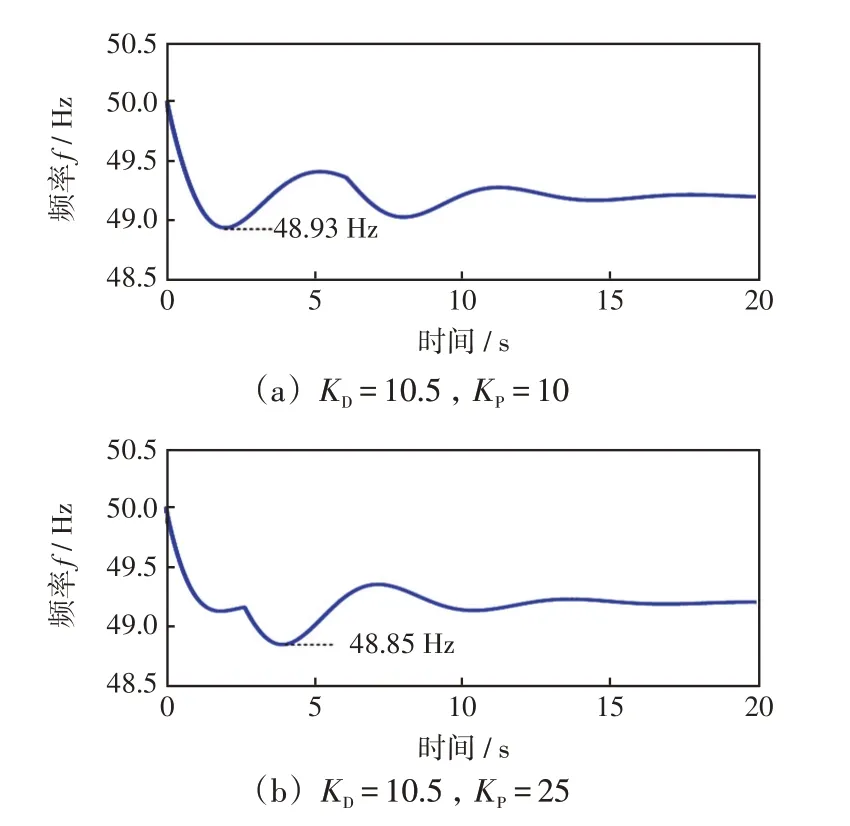
图7 当DFIG 调频参数不等于优化选值时系统在ΔPE=-0.2 扰动下的频率波形Fig.7 Frequency waveforms with the regulation of DFIG when KD and KP are not optimized and ΔPE= -0.2

如图7（a）所示，较小的系数KP使DFIG在功率扰动时未能及时充分参与调频，导致频率扰动后首次跌落较大，同时最低点达到48.93 Hz，但是，正因此时DFIG 的额外出力较小，使得频率二次跌落小于首次跌落，频率后段动态过程相对平滑且波动较小。相反地，如图7（b）所示，较大的系数Kp使DFIG 在功率扰动开始时便充分参与调频，从而大幅抬升首次频率跌落，但与此同时，由于风机出力较大，DFIG停止频率支撑后使频率二次跌落过大，进而导致频率最低点出现在频率二次跌落的过程中，达到48.85 Hz。在上述两组非最优KD、KP设计下，系统频率最低点均低于最优KD、KP设计下49.03 Hz的频率最低点，这验证了所述DFIG调频控制参数设计方法的正确性。

第3.1节最优KD及KP是在额定风速下设计得到的，鉴于风电的间歇性，当实际风速发生变化时，DFIG的调频性能也将受到影响。以风速vW等于0.85倍额定风速为例，得到频率仿真波形如图8所示。

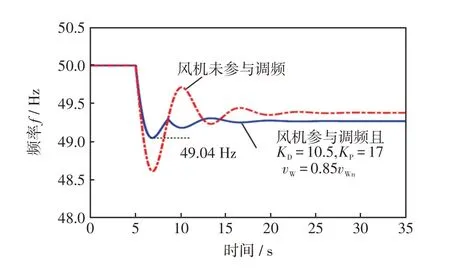
图8 KD=10.5、KP=17 时系统在0.85 倍额定风速及ΔPE= -0.2 扰动下的频率波形Fig.8 Frequency waveforms with the regulation of DFIG when KD=10.5,KP=17,vW=0.85vWn,and ΔPE= -0.2

由图8可见，相较于图5，在风速低于额定风速的条件下DFIG 可用于调频的转子动能降低；低风速虽然导致两次频降程度有所差异，但也增加了同步发电机在稳态下的出力，从而增强了系统等效惯量及阻尼，因此，所述优化设计方法仍将频率最低点由48.61 Hz抬升到49.04 Hz。

基于表2 系统基本参数设置，验证所提方法在不同新能源占比R及额定风速下的优化效果。在低新能源占比R=0.1、ΔPE=-0.2 下得最优调频控制参数KD=7.5、KP=30；在高新能源占比R=0.3、ΔPE=-0.2 下得最优调频控制参数KD=10.5、KP=4，两者的仿真波形如图9所示。

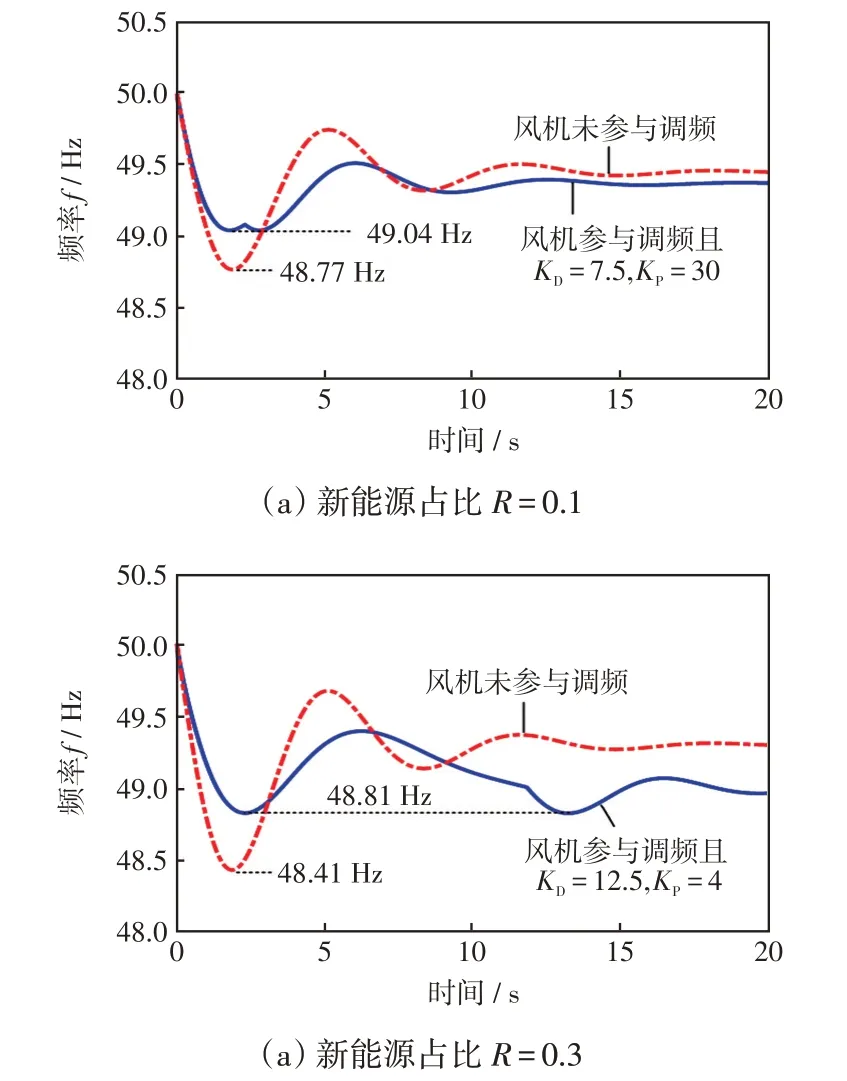
图9 当新能源占比R=0.1 和R=0.3 时系统在ΔPE= -0.2扰动工况下的频率波形Fig.9 Frequency waveforms when R equals 0.1 or 0.3 and ΔPE= -0.2

综合图5 和图9 可知，在新能源占比R较小的工况下，同步发电机占比更高、系统等效惯量阻尼更大，相同功率扰动下的系统频率最低点更高。随着新能源占比R从0.1到0.3，较大的R拉长了两频率最低点的时间间隔，同时使得稳态下的频率偏差问题更加突出，但所提优化方法在风机转子惯性与系统整体惯性不同比例时，仍可取得抬升暂态频率、改善系统频率安全稳定的效果，其稳态偏差问题可以通过AGC等手段解决。

以上仿真结果说明，为实现风机调频后功率扰动下系统具备最小的频率偏差，需通过设计KD、KP使两次频率跌落的最低点大致相当，同时，该参数方法设计能满足多种场合下系统对频率安全约束的要求。

4 结 论

（1）将DFIG转子动能优化控制的过程划分为转子转速达到限值前后两个阶段，并结合DFIG在虚拟惯量阻尼控制下参与调频的电网频率动态模型，构建了优化DFIG调频参数的目标函数和约束条件。

（2）设计DFIG调频控制参数，满足大功率扰动过程中系统具备大小相当的两次频率跌落的条件，将从最大程度上抬升频率最低点。该方法在不同新能源占比、不同功率扰动及不同风速下均具有良好的适应性。

（3）相较于DFIG 未参与频率支持或非最优参数，所述方法充分降低了低频减载风险，并保证了多运行工况下的频率安全。