木板的运动是简谐运动吗

王伟民 于方超

(1. 安徽省太和县宫集镇中心学校,安徽 太和 236652; 2. 广东省佛山市顺德区伦教中学,广东 佛山 528308)

1 一个有趣的运动现象

能够绕轴自由转动的两个相同的圆柱体A和B,它们的轴分别固定在两个水平的平行位置,如图1所示(图1看到的是两个圆柱体的横截面,其侧面向画面的里面延伸,所以看不到其侧面了),用一根皮带绕成“∞”字型连接两个圆柱体,并将皮带拉紧.这样,当一个圆柱体快速转动时,会带动另一个圆柱体按相反的方向快速转动.将其中的一个圆柱体再用一根皮带与电动机的轮子相连(图中没有画出),给电动机通电之后,两个圆柱体就会沿不同的方向快速转动.改变电动机轮子的转动方向,可以改变两个圆柱体的转动方向.

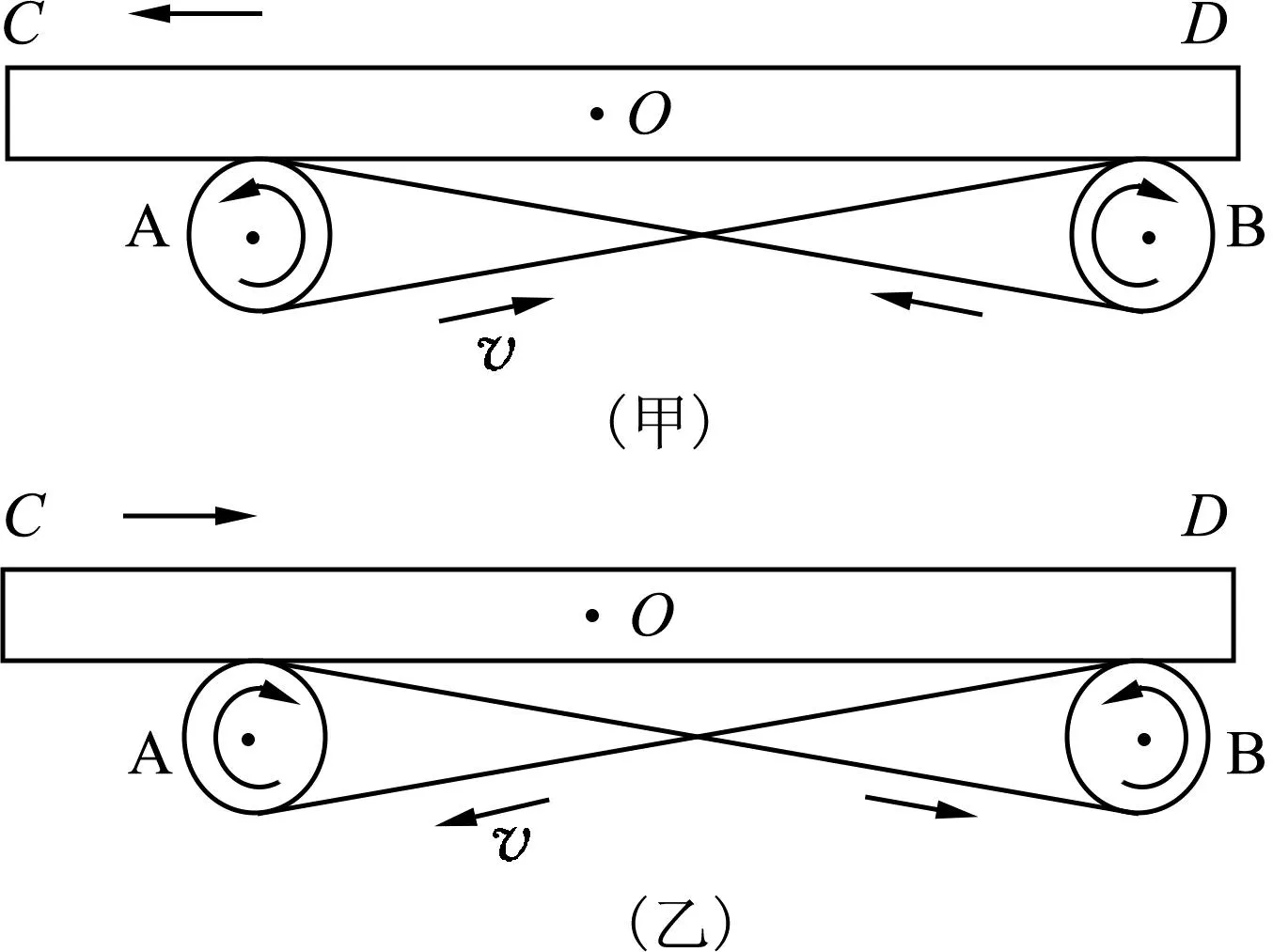
图1 木板在两个反向转动轮子上左右运动图示

将一块长木板(长度大于两个圆柱体轴心之间的距离)放在两个圆柱体上,调整两个圆柱体的转动方向和长木板相对圆柱体的位置,会发现,当左边的圆柱体A按逆时针方向转动、右边的圆柱体B按顺时针方向转动时,如图1(甲)所示,除非长木板CD的重心恰好在两个圆柱体的正中间位置,木板可以相对两个圆柱体的轴心保持静止不动的状态,其他情况,只要木板重心位置偏离两个圆柱体的中间位置,木板放上之后都会向远离两个圆柱体中间位置的方向运动,直至最终离开圆柱体.这种现象的成因也容易理解——当长木板的重心刚好位于两个圆柱体的正中间位置时,两个圆柱体对木板的压力相等,都等于木板重力的一半,由于A和B是相同的圆柱体,所以,两个圆柱体侧面与木板之间的动摩擦因数相同,因此,两个圆柱体对木板滑动摩擦力的大小相同,方向相反,并作用在同一条水平直线上,是一对平衡力,在这对水平平衡力的作用下,静止的木板会一直保持静止状态.当木板重心偏离两个圆柱体中间位置时,例如,木板重心在两个圆柱体中间位置的左边,则圆柱体A对木板竖直向上的压力大于圆柱体B对木板竖直向上的压力,所以,圆柱体A对木板向左的摩擦力大于圆柱体B对木板向右的摩擦力(以下均按圆柱体转动很快,木板相对圆柱体都是滑动的情形进行的讨论.如果圆柱体转动得比较慢,两个圆柱体对木板的两个摩擦力可能都是滑动摩擦力,也可能其中一个是滑动摩擦力,而另一个是静摩擦力),所以,木板所受两个圆柱体对其滑动摩擦力的合力方向向左,木板会相对圆柱体轴心向左加速运动,直至最终离开圆柱体.

如果左边的圆柱体A按顺时针方向转动,右边的圆柱体B按逆时针方向转动,如图1(乙)所示,把长木板放到两个圆柱体上面之后,若木板重心刚好在两个圆柱体的正中间位置,则木板相对两个圆柱体的轴心保持静止状态.当然,这依然是因为木板受到两个圆柱体对其方向相反的两个滑动摩擦力是一对平衡力.若木板放上之后,其重心偏离两个圆柱体的中间位置,则我们会看到一个非常有趣的物理现象——长木板在两个圆柱体上面不停地左右来回运动,如同秋千在吊绳下来回摆动的现象.我们不禁要问,此时木板的左右运动是简谐运动吗?

2 对一般情形下木板的运动问题进行分析

可以发现,上述现象给出的物理情景很特殊——水平木板在受到两个反向转动的轮子对其方向相反的水平外力作用下的运动.为使推理的结论更具一般性,我们不妨研究一般情形下木板的受力振动规律.

如图2所示,将木板CD放在两个轴心位置固定水平平行且快速旋转的圆柱体A和B上(旋转方向如图所示,为简化作图,我们用线段CD来替代木板,并认为其重心在木板的底面),木板与水平面的夹角为α,木板与两个圆柱体相切,切点之间的线段长度MN=L,木板重力为G,与圆柱体A、B之间的动摩擦因数分别为μ1、μ2.先确定木板受到平衡力时的位置,假设木板受到平衡力时,圆柱体A和木板的切点M到木板重心O的距离为MO=a,分别以N、M为支点根据杠杆原理,可得

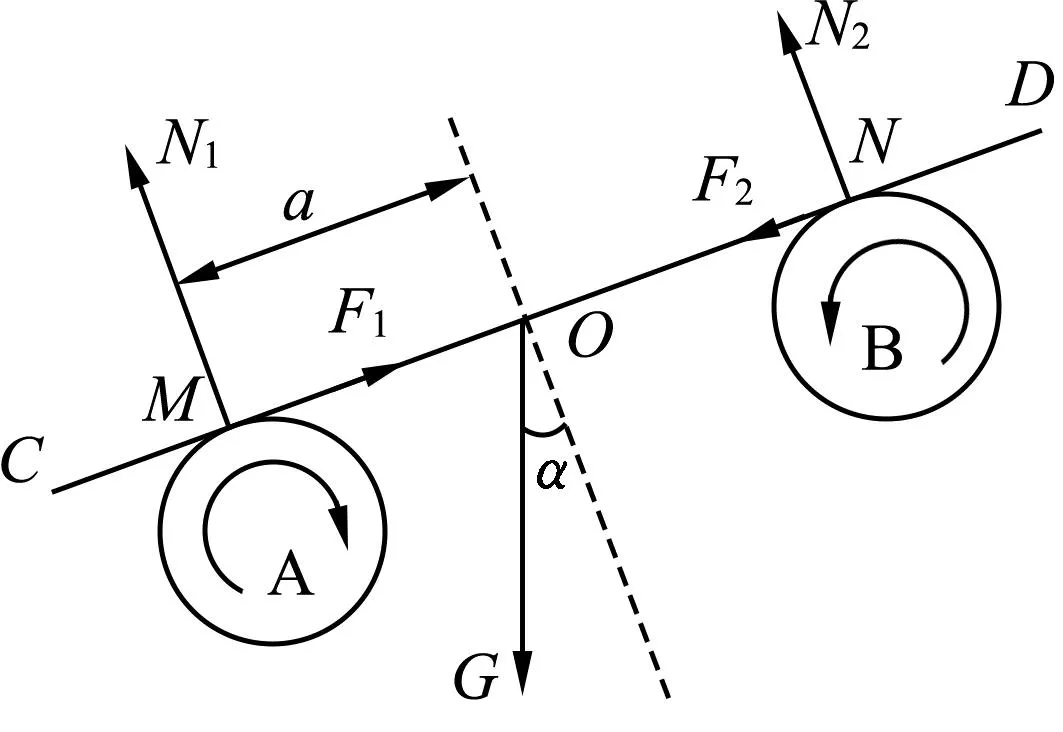
图2 木板倾斜受力平衡图示

N1L=G(L-a)cosα,N2L=Gacosα.

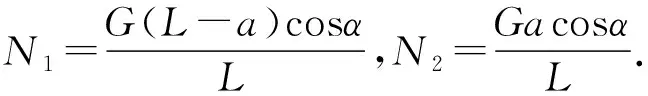
因此A、B两个圆柱体对木板的滑动摩擦力大小分别为

木板CD平衡时,它在CD方向上所受的合力为0,故有

F1=F2+Gsinα,即

解得

可整理为

(μ1cosα-sinα)L=a(μ1+μ2)cosα.

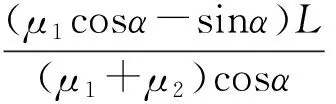
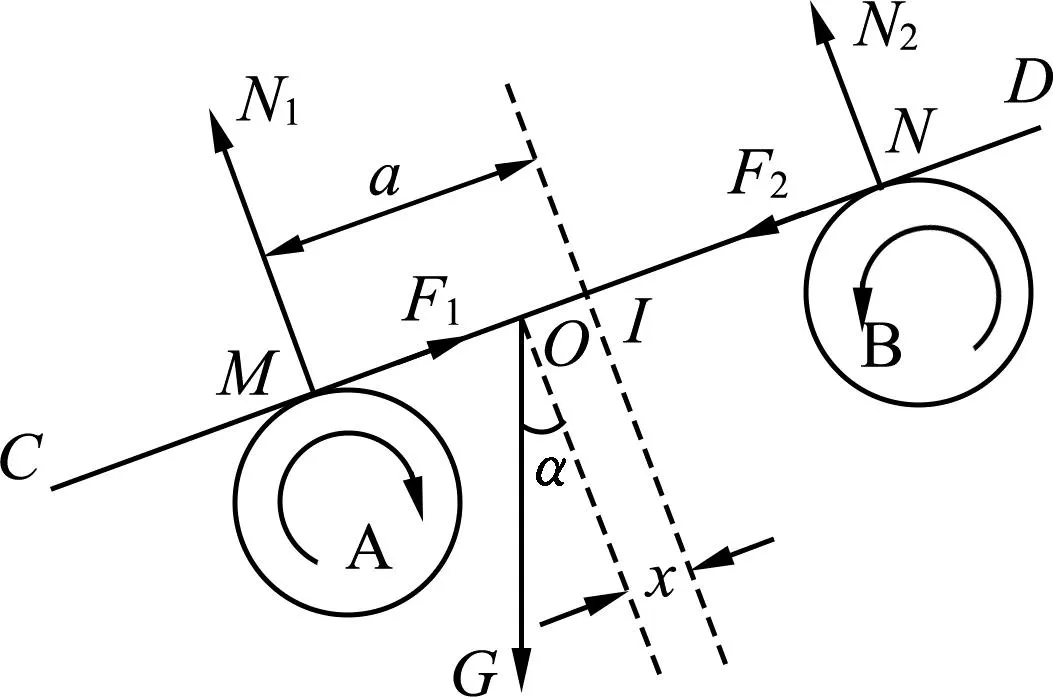
图3 木板倾斜状况时受力示意图

木板所受两个圆柱体滑动摩擦力的大小分别是

因此,在木板所在直线的方向上,木板所受各力合力大小为(方向指向平衡位置)

F=F1-F2-Gsinα=

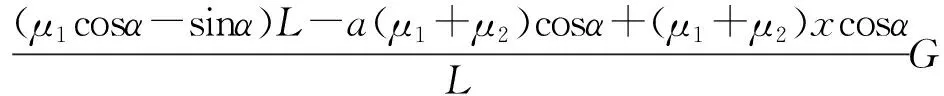
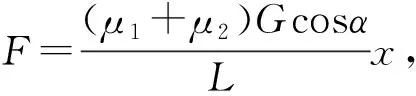
当然,我们这里的讨论,是把木板作为没有厚度的线段来进行分析,相当于把木板重心平移到其下表面而进行的定量推理,而实际的木板肯定有一定的厚度,其重心一定不在木板的底面上,那么,上面我们总结的木板做简谐运动的规律在实际情形下还成立吗?

如图4(甲)所示,木板的重心本来在其内部的O点,如果我们将其向下平移到木板的下表面,如图4(乙)所示,显然,木板重力的作用线(是直线)相对M、N这两点的位置没有发生任何变化,而我们上面的定量推理,凡是涉及木板重力的问题,只用到了M、N两点相对木板重力作用线的距离,所以,木板重心不要说平移到下表面,即使上下平移到空间内的其他任意点,也不影响我们结论的正确性.

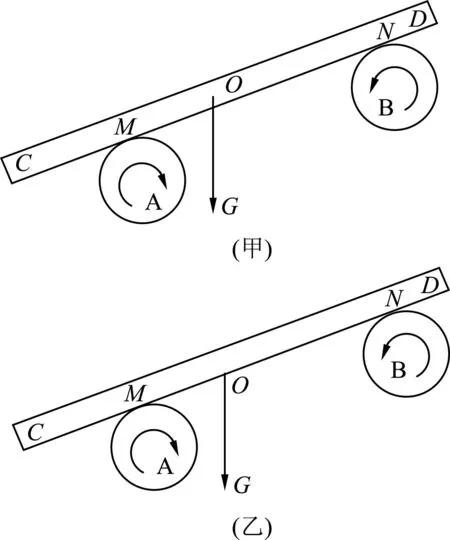
图4 木板重心上下平移示意图

3 木板的运动周期

对于木板在两个水平圆柱体上左右振动的现象,如果给出相关的必要条件,根据简谐运动的周期公式,可以求出木板的振动周期或频率.

例1.如图5所示,两个可以绕轴快速转动的圆柱体A和B,截面半径都是50 cm,将它们紧压在一起,并保持轴线水平平行,按图示方向快速转动时(A顺时针方向转动,B逆时针方向转动),将一个长度大于1 m的长木板轻轻放在两个圆柱体上面,会发现木板在两个圆柱体上不停地左右运动,已知A、B两木板与圆柱体之间的动摩擦因数分别为μ1=0.25和μ2=0.15,试求木板左右振动的运动周期?(结果可以保留无理数,取g=10 m/s2)

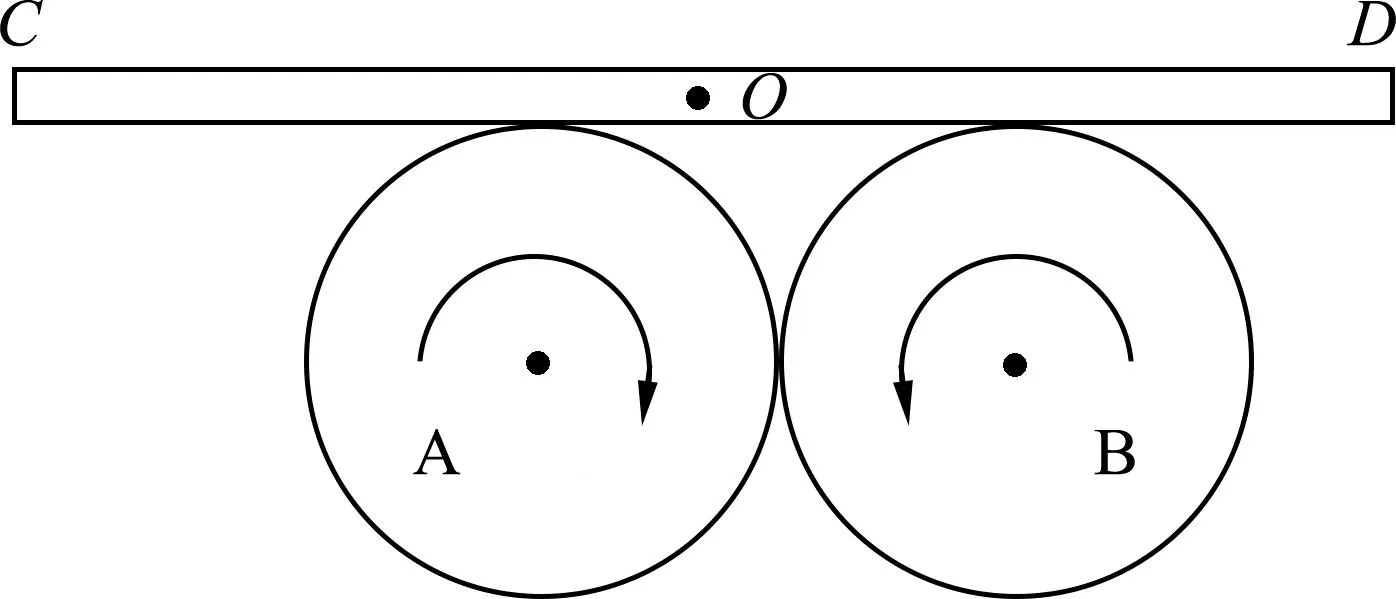
图5 木板在两个侧面相切圆柱体上运动图示

解析:与图1所示的问题相比,例1给出的物理问题不是用皮带连接两个圆柱体,而是将两个圆柱体紧紧压在一起转动.虽然形式上不一样,但二者提供的运动方式效果是相同的,都可以使得两个圆柱体按相反的方向转动,所以,例1给出的物理问题中,木板在两个圆柱体上方的左右运动依然是简谐运动,我们仍然可以运用上述推理出的木板受力公式进行相关计算.

依题意可知,木板所受两个圆柱体摩擦力的作用点,是圆柱体的侧面圆与木板的两个切点,两切点之间的长度为L=1 m,木板水平,说明木板与水平面的夹角为α=0,设木板的质量为m,则木板左右运动的运动周期为

即木板在两个圆柱体上左右运动的周期是πs.

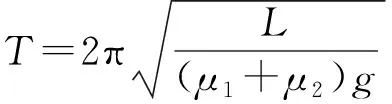
4 结语

需要说明的是,以上分析总结木板的振动规律,仅仅是形式上的简谐运动,跟弹簧振子的简谐运动还有本质的区别——弹簧振子在振动过程中,不仅形式上是简谐运动,而且在振动过程中弹簧和小球组成系统的机械能守恒.而上述木板在振动过程中,两边对木板施加滑动摩擦力的两个圆柱体,一个对木板做正功的同时,另一个在对木板做负功,系统的机械能不守恒,系统消耗外界机械能的同时,以摩擦做功的方式转化成了内能.