一种SOP端口不平衡时直流侧电压脉动抑制策略
张国荣, 汤彬, 沈聪, 王泰文, 徐晨林, 夏子鹏
(1.合肥工业大学 电气与自动化工程学院,合肥 230009; 2.广东电网有限责任公司珠海供电局,广东 珠海 519031)
0 引 言
随着以太阳能和风能为主要代表的新型能源的大规模的使用,分布式电源(DG)接入到配电网中来,给配电网带来了广泛而深刻的影响[1]。配电网中电压越限、双向潮流和继电保护灵敏度失衡等问题,对系统的稳定性和安全性造成了重大的影响[2]。面对日益复杂的电网条件,传统的手段已经无法提升配电网的电能质量[3],因此,主动配网技术和利用电力电子设备来对配电网进行优化调节等技术成为了研究的热点。
柔性开关设备因其对配电网有着重要的影响而备受关注。2009年,文献[4-5]提出了一种基于电力电子技术的新型装置SNOP(soft normally open point)的概念,用来代替部分配电网中的联络开关、分段开关。柔性多状态开关可实现馈线间的常态化柔性连接,避免了传统开关受开关次数限制和只有通断两种状态的问题,从而具备了更加灵活、快速的功率交换能力[6]。
国内外学者对SOP(soft open point)的研究目前大部分都集中在柔性多状态开关的优化和控制策略方面。文献[7-8]对SOP的运行原理做了相关阐述。文献[9]针对主动配电系统的运行提出了一种优化的SOP配置方法。文献[10]针对SOP的数学模型提出了一种将反馈线性化和滑模控制相结合的控制策略,提升了传统控制策略的动态性能和鲁棒性。文献[11]提出了一种将SOP和储能系统联合的方法对有源配电网进行优化,提高了配电网运行的可靠性和经济性。文献[12]提出一种采用控制器状态跟踪的控制方法,来实现三端口的FMSS的不同控制模式下的切换。文献[13]针对含SOP的配电网恢复问题,采用二阶锥规划解决SOP的控制模式切换问题,提出了一种SOP和联络开关协调恢复供电的策略。文献[14]提出一种包括SOP在内的配电网运行优化模型,并从动态、静态潮流优化方面验证了SOP的优势。
在SOP的各个端口中,工作在Udc-Q模式下的端口,在维持系统的功率平衡中起关键作用,如果该端口发生故障或者不平衡时,直流侧电压会发生波动,进而对整个系统造成不稳定的影响[15]。目前,对于不平衡下直流侧电压脉动抑制的研究主要集中在微电网方面,而对于SOP端口不平衡时直流侧电压脉动的抑制暂未有文献涉及。文献[16]提出了一种当交流电网电压不平衡时AC-DC换流器的控制策略,以消除注入电网的有功功率波动为目的,来消除直流侧电压波动。文献[17]针对不平衡负载时微电网电压波动情况,通过分析其产生的原因,提出了一种基于超级电容器的直流电压抑制策略。
文中以三端口SOP为研究对象,首先分析了SOP的数学模型,对Udc-Q端口电压不平衡时,直流侧电压波动的产生原理进行了分析。根据SOP的拓扑结构,提出了一种基于二阶滑模控制的直流侧电压波动抑制策略[18],消除系统抖振。利用基于非线性干扰观测器的电容补偿器装置来实现信号的追踪和对直流电压波动的抑制[19]。最后,根据不同的不平衡条件,在MATLAB/Simulink中搭建SOP仿真模型,以验证所提方法的有效性。
1 SOP建模分析
1.1 接入拓扑
SOP作为一种新型的电力电子装置,主要由全控型器件组成。SOP的接入方式一般有两端口和多端口的系统结构,图1给出了两端口接入拓扑。由于两端口的接入方式存在着一些局限性,现在大多采用的是三端口的接入拓扑,如图2所示。文中主要以三端口SOP为研究对象。

图1 两端口SOP接入拓扑

图2 三端口SOP接入拓扑
随着SOP端口数量的增加,使得其在接入配电网的形式更加的灵活。SOP接在馈线末端,可以实现不同馈线之间的柔性互联,具有闭环运行的优点,增加了供电系统的可靠性。
1.2 三端口SOP的数学模型
三端口SOP主要依靠背靠背电压源变流器来实现,其三端口呈对称结构,由三个相同的VSC来构成,通过直流侧的公共电容相连接。其拓扑结构如图3所示。

图3 端口VSC主电路拓扑
设三相电网电压平衡,当输出的端口采用L滤波时,则可建立其在三相静止坐标系下的数学模型为:
(1)
式中j为a、b、c;Sj为任一相的开关函数,当其值为1时表示上桥臂导通,下桥臂关断,当其值为0时表示下桥臂导通,下桥臂关断;ij为VSC的输出电流;Uj为VSC的输出电压;Uvj为交流侧系统电压;Udc为直流侧电容电压。
因为SOP的三个端口连接在同一个直流侧电容上,则其电流满足方程:
(2)
式中idcx为端口x的直流侧母线电流;Stx为端口x的某相开关函数;itx为端口x的某相输出电流。
当忽略变流器的损耗时,则有方程:
(3)
式中Px为端口x的有功功率。
当系统稳定运行的时候,各端口的直流侧母线电压恒定,由式(2)可知其和为0,那么再结合式(3)可得:
(4)
由式(4)可知,在SOP稳定运行时,忽略变流器的损耗,系统的输入有功功率与输出有功功率相等,即功率平衡。
2 直流侧电压脉动抑制策略
在SOP的三个端口中,工作在Udc-Q模式下的变流器是整个装置中最薄弱的环节,当其前端馈线发生不平衡时,会引起直流侧电压的波动,进而影响整个系统的稳定性,以工作在Udc-Q端口下的变流器为例分析它在不平衡下的状况,在端口直流侧并联补偿装置,分析其电压补偿情况,补偿装置如图4虚线框内所示。

图4 Udc-Q补偿装置
图4中:Psc为补偿装置的补偿功率;S1,S2是两个功率开关管;Ldc,Usc分别为补偿电感和补偿装置的端电压。
忽略变流器上的损耗,则整个系统的直流侧电容的功率可表示为:
(5)
式中Pu,Qu为Udc-Q端口前端的有功、无功功率;Pk为另外两个端口的功率和;C为直流侧电容。
为了简化计算,定义:
(6)
则式(5)可以简化为:
(7)
pu=pg+pn
(8)
当三个端口平衡时,滤波器上均无损耗,则有式(7)成立,当Udc-Q发生不平衡时,既Uga、Ugb、Ugc不对称时,则Udc-Q端口会出现负序电压、电流分量[19]。在两相静止坐标系下,由瞬时功率理论可得:
pg=pg0+pgc2cos(2ωt)+pgs2sin(2ωt)
(9)
式中pg0为有功功率的稳态值;pgc2、pgs2为有功功率2倍频的正、余弦分量。
另有:
(10)
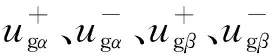
当负序电流流过电感时,会在上面产生相应的脉动功率,为:
pn=pnc2cos(2ωt)+pns2sin(2ωt)
(11)
其中:
(12)
将式(12)进行综合,可得:
(13)
由式(13)可以看出,当Udc-Q端口出现不平衡时,直流侧端口将出现2倍频的功率脉动,进而引起直流侧电压的脉动,同样的,若其他两个端口也出现不平衡时,也只是在此基础上增加2倍频的脉动分量。
当Udc-Q端口馈线出现电压不平衡时,馈线电压中会出现负序分量,变流器的输出电流、输出功率都会出现2倍频率的波动[19]。
在两相静止坐标系下,换流器的输出功率可根据瞬时功率理论得到如下方程:
Pu=Pu0+Pui2+Puu2
(14)
式中Pu0,Pui2,Puu2分别表示为换流器的有功功率的稳态值和2倍频电流、电压引起的波动值。在设计系统的控制策略时,考虑电流的正弦化,电流的负序分量被消除,则系统中只剩下了脉动的2倍频电压分量,产生Puu2,进而引起直流侧的电压的脉动。采用在直流侧电容上并联如图4虚线内的电压补偿装置,吸收不平衡的功率脉动,来消除脉动的电压。
当加入上述的补偿装置后,则式(7)可为:
(15)
补偿装置将2倍频电压引起的功率波动弥补,即Psc=Puu2,则:
(16)
补偿装置将脉动的功率补偿之后,SOP直流侧的电压波动将被抑制。
3 基于非线性干扰观测器的补偿装置
3.1 电容补偿器原理
引入非线性干扰观测器,通过对直流侧电压和电容补偿器的信息,可以实现对功率的快速跟踪,使的获得的补偿信息更加的快速准确,进而使得电压脉动抑制效果更佳。
为了得到补偿的脉动功率,忽略换流器上的功率损耗,则对于图4所示的系统,其直流侧电容方程为:
(17)
式中is=ik-iu,由式(17)看出,要想得到补偿功率Psc必须得到is。
补偿器的动态方程为:
(18)
定义:
(19)
式中x1,x2为状态变量;u是控制输入;d(t),y分别为系统扰动和系统输出。
则上述系统可重新定义为:
(20)
式中:
(21)
可设计如下的非线性干扰观测器对其中的扰动量d(t)进行观测[20],可对内部扰动实现快速的跟踪:
(22)

p(x)=l1x1+l2x2
(23)
非线性干扰观测器的增益如式(24)表示:
(24)

(25)
当满足条件l(x)g2(x) >0时,干扰观测器的误差是收敛的。
令l1=0,l2>0,且在满足上述收敛条件的情况下,可以简化控制系统中观测器的设计和消除一些其他不确定因素的影响。对观测器的控制进行整理,可得到Buck和Boost模式下统一的非线性干扰观测器的形式:
(26)
由式(11)可得:
(27)
3.2 滑模控制
补偿装置的控制方式使用二阶滑模控制,可以抑制系统的抖振,除去相对阶的限制和提高控制的精度[21]。
根据系统的控制目标,将跟踪误差和电流的参考值分别定义为:
(28)
(29)
滑模控制的控制效果的好坏,与滑模面的选择有重大的关系[22],传统的线性滑模面中存在着稳态误差,会引起系统的抖振,文中选择在传统的滑模面中增加积分项,来克服系统的抖振,使得系统具有良好的滑动模态。选择积分滑模面,定义为:
(30)
式中Ki是积分系数,是正实数。
采用二阶滑模控制(SMC),通过控制开关管S1和S2的导通,定义控制变量:
D=Deq+ΔD
(31)
式中Deq、ΔD分别为等效控制和开关控制。Deq的作用是使系统的状态保持在滑模面上,ΔD的作用是保证系统可以在有限时间内到达滑模面。
当Psc< 0时,电容器要充电,此时补偿器工作在Buck模式下,通过计算可得其开关控制为:
(32)
其等效控制可表示为:
Deq=(Usc-Ldc-Kies)/Udc
(33)
则总的控制输入为:
D1=Deq+ΔD1
(34)
当Psc> 0时,电容器要充电,此时补偿器工作在Boost模式下,通过计算可得其开关控制为:
(35)
其等效控制可表示为:
Deq=(-Usc+LdcKies)/Udc+1
(36)
则总的控制输入为:
D1=Deq+ΔD1
(37)
由于补偿装置的充放电过程对称,所以有k11=k21,k12=k22。
根据上述公式推导,得到控制器的控制框图如图5所示。

图5 补偿器的控制框图
4 仿真验证
为验证文中所提当SOP端口不平衡时的直流侧脉动和直流侧电压脉动抑制策略的有效性,在MATLAB/Simulink中搭建三端SOP仿真模型。
对直流侧电压2倍频脉动的验证:一开始系统处于正常运行状态,在t=0.05 s时,Udc-Q端口的电压跌落30%,得到如图6所示直流侧电压脉动图,与图7两个端口均跌落50%时的直流侧电压脉动图进行对比可发现,多个端口的不平衡不影响直流侧电压脉动的频率,只是改变了其幅值的大小。图8为另一侧电压滞后Udc-Q端口30°相位时的直流侧电压脉动,均可看出,多端口不平衡时,直流侧电压脉动仍为2倍频。
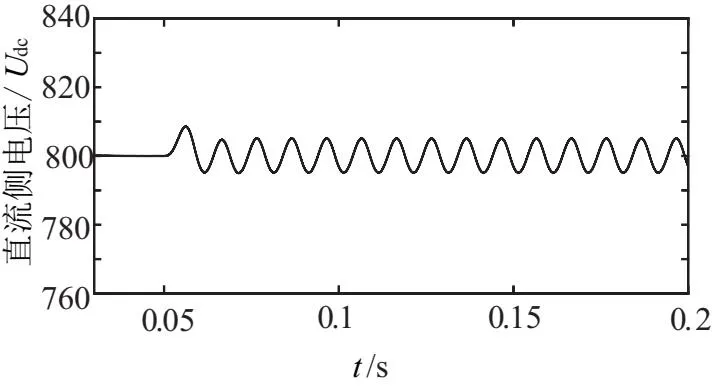
图6 直流侧电压Udc

图7 直流侧电压Udc

图8 直流侧电压Udc
直流侧电压脉动抑制的验证:
正常运行时,2端口运行于Udc-Q模式,另外两端口运行于P-Q模式,当端口2不平衡时采用所提策略,抑制直流侧电压波动。仿真模型参数如表1所示。

表1 SOP系统参数
根据端口不平衡时直流侧的电压脉动和功率脉动,得到补偿器和控制端口滑模控制的参数,如表2所示。
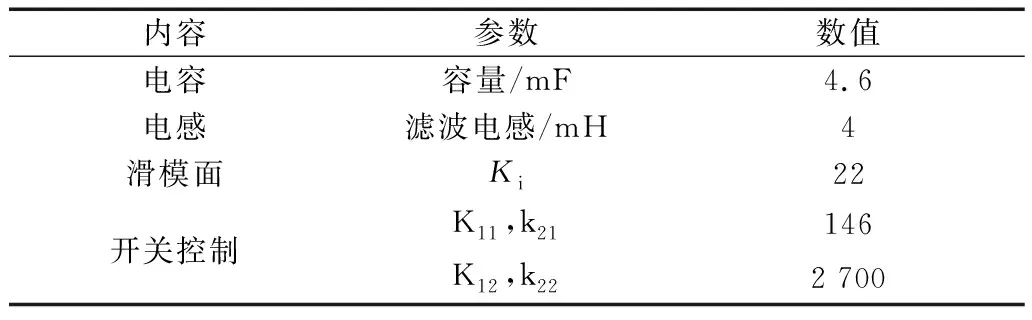
表2 控制端口参数
仿真工况1:三端口SOP一开始运行于正常状态,t=0.02 s时,Udc-Q端口馈线的C相电压跌落30%,图9所示为Udc-Q端口三相电压波形图。

图9 Udc-Q端口三相电压
端口电压不平衡使的直流侧电容发生脉动,由于Udc-Q端口的特性,当其发生脉动时会严重影响整个系统的稳定性。图10所示当端口不平衡时直流侧电压Udc脉动情况,在t=0.07 s时投入补偿装置,可看出补偿装置的补偿效果很明显。

图10 直流侧电压Udc
图11是将非线性干扰观测器去掉而直接测功率,得到的直流电压脉动抑制图,与图10相比,可看出加了干扰观测器以后的补偿效果更佳的好,对直流电压的脉动抑制幅度更大。图12为补偿装置的补偿功率,通过吸收脉动的功率,达到抑制直流侧脉动的目的。
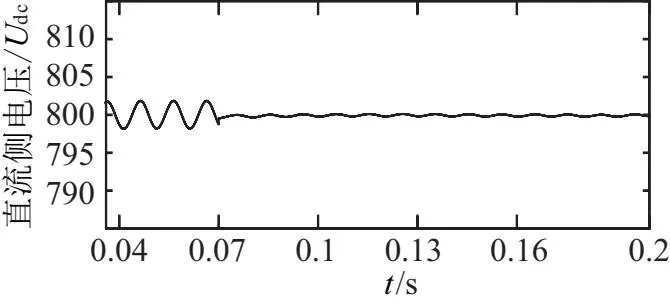
图11 未加干扰观测器直流侧电压Udc

图12 补偿功率
仿真工况2:三端口SOP一开始运行于正常状态,t=0.02 s时,Udc-Q端口馈线的C相电压跌落50%,图13所示为Udc-Q端口三相电压波形图。

图13 Udc-Q端口三相电压
同样的,在t=0.07 s时投入补偿装置,通过观测直流侧电压脉动情况来检测补偿装置的效果,图14为直流侧电压脉动图,图15为不加干扰观测器时的直流侧电压脉动图,与图14对比可看出加观测器的抑制效果更好。图16为补偿装置补偿功率图,可看到补偿效果,和抑制直流侧脉动效果均很好。

图14 直流侧电压Udc
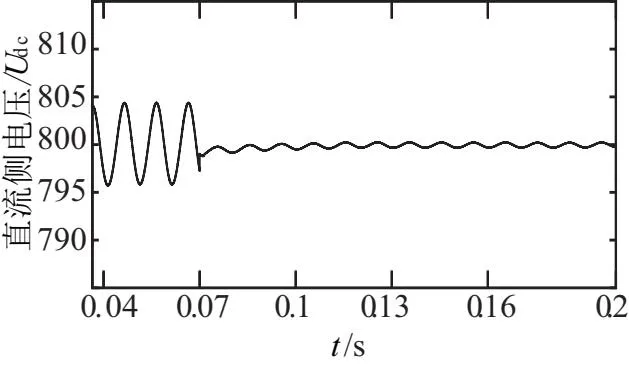
图15 未加干扰观测器直流侧电压Udc

图16 补偿功率
SOP端口在两种不同电压不平衡情况下直流侧电压均有波动,通过补偿装置,很好的抑制了由于端口不平衡所带来的直流侧电压脉动,验证了所提策略的有效性。
5 结束语
在SOP端口不平衡时,提出一种策略来对直流侧脉动的电压进行抑制。
1)当SOP端口不平衡时,会引起直流侧电压脉动,对系统稳定性有严重影响。
2)提出的基于非线性干扰观测器的补偿装置,对SOP端口多种不同不平衡情况所引起的直流侧电压波动均能进行有效抑制。所提控制策略在很短时间内即可达到稳定,反应快速,所抑制直流电压波动很小,效果显著。
3)所提策略简单易于实现,可以提高SOP的稳定性,具有一定的工程应用价值。

