基于双重熵值修正指标权重的电能表状态评价研究

黄天富,李建新,吴志武,王春光

(国网福建省电力有限公司营销服务中心,福州 350013)

0 引 言

电能表是进行电量贸易结算的重要工具,其状态影响着电量结算的准确性。确保电能表稳定、可靠运行,直接关系到电量交易客户的合法权益[1]。

目前,在电能表状态评价工作上,已有了一定的研究工作[2-5]。文献[6]根据目标导向原则,建立了分层次的电能表状态评价指标体系,提出了一种基于可靠性的状态检验技术;文献[7]提出了一种融合安全域的电能表状态评估新方法;文献[8]从电能表的基础状态、检测、监测和家族缺陷等多方面,提出了一种电能表状态在线综合评价方法;随着大数据技术的发展,文献[9-10]采用了决策树群技术,对多维电能表的状态进行检验;文献[11-12]提出一种基于贝叶斯网络的电能表状态评估方法,提高了评估效率。

然而,电能表状态评价的研究工作,还处于初步阶段。电能表状态的评价标准不一,没有一个完整、全面、成熟的综合评价体系。

此外,电能表状态评价中,关键的指标权重确定依赖于专家的主观评分。当存在专家误判时,将会影响指标赋权结果的合理性[13-15]。如何建立科学、合理的指标赋权模型,同时兼顾评价指标的客观规律性和主观经验性,对提高电能表状态评价的准确性非常重要。

另一方面,随着电网规模的扩大,电能表数量不断增多,导致电能表的运维管理工作量也在不断增大。根据行业管理要求,现行的电能表检验周期固定,可能更换能继续使用的电能表,或者检验后电能表的状态变差,造成人力和物力资源的浪费。因此,需要对电能表的运行状态进行科学、准确的综合评价,以便指导实际检修工作。

有鉴于此,文中梳理并构建了一个全面、合理的电能表状态评价指标体系,探索了一种兼顾指标经验性的同时减少了主观随意性的指标赋权方法,由此提出了一种电能表状态评价模型。同时结合现场经验和电能表状态评价结果,给出了一种灵活的电能表检验策略建议。

1 电能表状态评价指标体系

1.1 指标体系的建立原则

选取科学、合理的指标是进行评价工作的重要基础,是准确进行评价的关键。

一个完备的指标体系应具有如下原则[16]:

1)系统性原则,即整体、全面考察多方面的影响和变化,所有指标形成一个完整、多面、严密、有机的体系。

2)可操作原则,即指标的含义明确,可通过数据和资料进行定性分析,或进行较准确的定量分析。

3)定量指标和定性指标相结合原则,定量指标可以减少主观判断上的随意性和模糊性,而定性指标可以弥补定量指标的不足。

4)独立性原则,即同一目标层的指标相互独立,尽可能减少指标之间的关联度,避免对同一目标的重复计算。

1.2 状态评价指标体系的建立

文中将电能表状态评价指标体系分为性能、可靠性、配置、工况4个维度,并选取合适的子指标来衡量优劣程度。其中,性能指标是评价电能表运行状态的核心指标,直接关系到电能表测量的准确性;可靠性指标包括家族缺陷和历史故障,家族缺陷包括了可靠寿命、年度返修率等范畴,历史故障包括了故障率、可靠度等范畴;配置指标可评价人为管理层面的优劣程度;此外,外部的工况和环境对电能表的运行状态也具有的影响,故单独作为一个维度考虑。

兼顾指标体系建立的系统性原则、可操作性原则、定量指标和定性指标相结合原则、独立性原则,对现有指标体系进行完善和筛选,建立的电能表状态评价指标体系具体如表1所示。

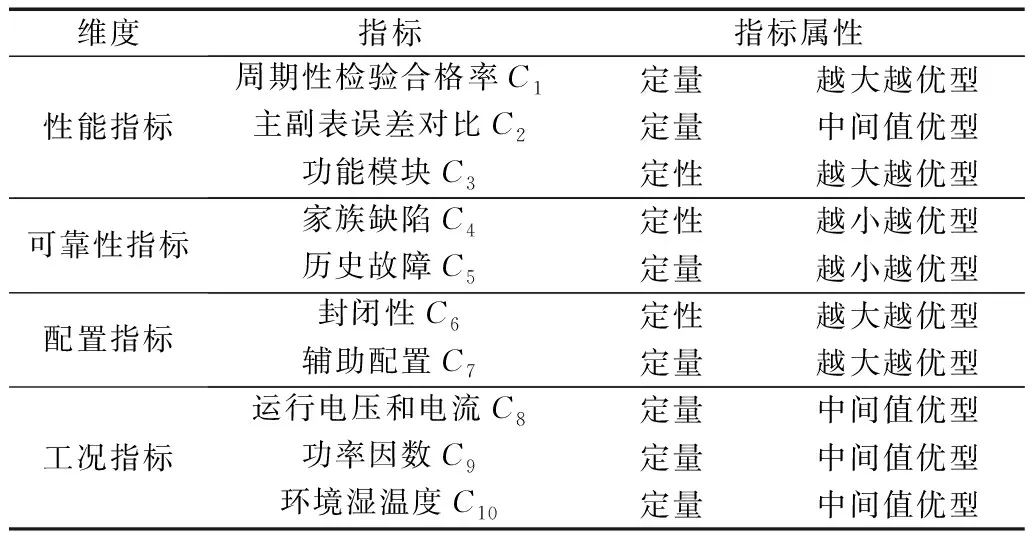
表1 电能表状态评价指标体系

文中的电能表状态评价指标体系,是在原有的评价指标基础上,进行了有机综合、提炼和一定程度上的创新,具有完备、合理性;另一方面,考虑了以现有的各项统计制度和数据为基础,具有可操作性。具体如,将文献[11-12]的指标“运行环境”,在工况指标维度中进行了具体细化,并剔除了“用户信誉”等不重要的指标;根据DL/T 448—2016《电能计量装置技术管理规程》,将文献[17]的指标“周期性检验实测值”,修改为“周期性检验合格率”,更能直观评价电能表的状态。

1.3 指标评分值的获取

对于表1中的定性指标,可直接根据专家的专业经验给出评分值。而对于定量指标,需要先确定指标评分模型,并将指标的数据表征结果代入评分模型,从而得到评分值。3种评分模型如下:

1)越大越优型,也称效益型指标,其评估状态量越高,指标表现越好。对应的评分模型图像如图1所示。

图1 越大越优型评分模型

对应的评分模型函数表达式为:

(1)

2)越小越优型,也称成本型指标,其评估状态量越小,指标表现越好。对应的评分模型图像如图2所示。

图2 越小越优型评分模型

对应的评分模型函数表达式为:

(2)

3)中间值优型,其评估状态量越接近中间值,指标表现越好。对应的评分模型图像如图3所示。

图3 中间值优型评分模型

对应的评分模型函数表达式为:

(3)

图1～图3中的横坐标对应定量指标的评估状态量的数据表征结果,纵坐标为经过归一化后,在0～1内的评分值。式(1)～式(3)中,x1～x4为评分模型参数,通常通过技术资料、规程规定、数学建模、专家经验等方法确定。

文章根据专家的评分样本数据,在迭代寻优中求取评分模型的最优参数。以越大越优型评分模型为例,具体为:

1)设评估状态量序列为J={j1,j2,……,jn},对应的专家评分序列为K={k1,k2,….,kn};模型参数初始设置为X0=(x1,x2)= (x1_0,x2_0),对应的初始评分函数为f(X0);

3)以最小化差值L为优化目标,采用传统粒子群算法,获取评分模型的最优参数。

2 基于双重熵值的指标权重确定

根据专家主观评分确定指标权重,存在很大的主观随意性,人为误判会对赋权结果产生负面影响。而基于信息熵原理确定指标权重的熵值法,可以避免人为因素的干扰,但会忽略指标的经验重要性[18-19]。

有鉴于此,本节对传统熵值法进行改进,提出一种基于双重熵值修正指标权重的电能表状态评价指标赋权模型。即基于相对熵修正电能表状态评价指标的重要性专家评分结果,提高评分结果的合理性;然后基于广义熵进一步修正G1法指标赋权,在减少主观随意性的同时兼顾了指标经验重要性[20]。

2.1 基于相对熵的专家评分合理性分析

假设n位专家(A1,A2,…,An)对m个指标(I1,I2,…,Im)进行评分,专家Ai对指标Ij的重要性评分为pij。

将所有专家的评分单位化,即:

(4)

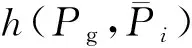
(5)

由熵值理论可知,式(5)的结果越小时,专家Ai与整个专家组的重要性评分越接近,表明评分合理性越高。

假设所有专家的初始权重wi为1/n,相对熵最小化约束的非线性规划为:

(6)

取Lagrange函数为:

(7)

令∇L(Pg,v)=0,有:

(8)

(9)

(10)

则专家Ai和专家群组Ag在指标Ij上的重要性评分差异Δdj为:

(11)

其评分差异用熵值计算如下:

(12)

进一步,专家Ai对所有指标的评分熵为:

(13)

由熵值理论可知,式(13)的结果越小时,该专家评分的不确定性越小,合理性越高。

如果某个专家的评分合理性较低,则应该将该专家的评分结果剔除,避免降低整个专家群组的评分合理性。

2.2 熵值修正G1法指标赋权

G1法对传统的层次分析法进行了改进。其避免了层次分析法的缺点,且无需一致性检验。

指标Ij的熵值ej计算如下:

(14)

式中yij为指标评价结果规范后的值。当指标的数值变异度越小/大时,代表其熵值就越大/小,指标权重越小/大。

根据修正后的指标重要性专家评分,各指标的重要性排位为:

(15)

(16)

最终,得到各指标的权重为:

(17)

3 电能表状态评价模型的构建

基于上述两节的分析,构建电能表状态评价模型,其具体步骤如下:

1)确定评价指标和等级。

从4个维度确立表征电能表状态的10个指标集合U={u1,u2,…,u10}(见表1),将电能表状态的评价结果分为5个等级,即V={v1,v2,…,v5}={优,良,一般,较差,差}。

2)确定指标的评判矩阵。

对各评价指标进行评分(见1.3小节),计算各指标的评判向量Mi=[mi1mi2mi3mi4mi5],即在权重介入之前,该指标属于各状态评价结果的可能性大小。各评判向量组成的指标的评判矩阵M,表示如下:

(18)

由于指标的属性和评分获取方法的不同,其中,定量指标的评判向量采取模糊聚类的方法计算[21],定性指标的评判向量采取灰色聚类的方法计算[22]。

3)确定各指标的权重向量。

基于相对熵理论评估专家评分的合理性,剔除合理性较低的专家指标评分。采用熵值修正G1法计算评价指标的权重向量,表示如下:

(19)

4)获得评价结果。

评价对象的决策集B计算为:

B=W·M

(20)

式中B={b1,b2,…,bj,…,bn},bj为评价对象在评价等级vj上的程度。

决策集B中最大的bj对应的评价等级vj,代表电能表状态的评价结果。

4 模型的应用分析

以我国某省近一年检测的电能表为例,对电能表状态评价模型进行测试分析。

根据第3节的具体步骤,先后确定评价指标、指标的评判矩阵、指标的权重向量,最终获得评价结果。有关数据来源于现场电能表检验仪表或专家评分。

以下主要介绍关键的指标权重获取过程,以及不同类别、不同批次电能表状态特征的评价结果。最后,与传统方法所得结果进行比较,突出文中所提方案的有效性和优越性。

4.1 指标权重的计算

邀请8位专家(A1～A8)对所有指标(C1～C10)的重要性程度以1～10分法评分,数值越大表明指标越重要,结果如表2所示。

表2 电能表状态指标专家评分表

假设8位专家的初始权重向量为wi=(0.125, 0.125,0.125,0.125,0.125,0.125,0.125,0.125),根据式(6)～式(10)迭代计算,误差为ε=0.000 5,得到电能表状态评价指标重要性的专家群组评分初始结果,结果如表3所示。

表3 专家群组评分初始结果

进一步,根据式(11)～式(13)计算每位专家的评分合理性,结果如表4所示。

表4 专家评分合理性分析结果

表4表明,专家A4的评分熵结果远远大于其他专家的评分熵,表明该专家的评分合理性较低,会影响整个专家群组的评分合理性。具体表现为,表2专家评分表中,专家A4对指标C2～C3、C5～C6的重要性评价与专家整体的评分差别较大。因此,需要剔除专家A4的评分结果,重新计算,以优化专家群组评分结果。

进一步,获得所有指标的评分值后,根据式(14)计算各评价指标的熵值,结果如表5所示。

表5 评价指标的熵值表

根据“熵值越大/小,指标权重越小/大”的原则,得到各指标的重要性排序为:

C1≥C5≥C2≥C3≥C4≥C6≥C7≥C9≥C8≥C10

(21)

最终,根据式(16)～式(17),可以计算获得所有指标的权重,结果如表6所示。

表6 评价指标的权重

4.2 电能表状态的特征分析

借助计算机工具,选取共1 120台电能表的状态进行评价,根据评分将评价结果分为5个等级,即V={v1,v2,…,v5}={优,良,一般,较差,差}。

4.2.1 评价结果按电能表类型划分

重点关注如下3类电能表,即:

1)I类电能表,220 kV及以上结算用电能表,要求每6个月现场检验一次。

2)II类电能表,66 kV～220 kV结算用电能表,要求每12个月现场检验一次。

3)III类电能表,10 kV～66 kV结算用电能表,要求每24个月现场检验一次。

将评价结果按不同的电能表类型分类,结果如表7所示。

表7 评价结果按电能表类型划分

表7表明,由于I类电能表所处的电压等级高,安全和经济责任大,故电能表的精度等级高、辅助配置更齐全,状态评价结果占优比也更多。另一方面,I类电能表微小的问题,都有可能造成严重的后果或经济损失,故电能表状态容易出现评价结果为“差”的等级。

进一步,对评价结果为“差”的21台电能表进行具体检查,发现分别存在主副表误差偏大、封闭性破坏、使用年限较长、运行工况不稳等问题,需及时处理或更换有关电能表,也表明文中电能表状态评价结果正确。

4.2.2 评价结果按投运时间划分

评价结果按电能表的投运时间划分,结果如表8所示。

表8 评价结果按投运时间划分

表8表明,整体上,随着电能表使用年限的增加,其可靠性会逐渐下降,即电能表状态评价结果的等级整体降低。具体表现为:

1)投运时间为0—3年的电能表中,由于新设备性能较好和及时的新安装检验,状态评价等级为“优”的占80%,没有评价等级为“差”的电能表。

2)投运时间为4年—6年的电能表中,状态评价等级为“优”的降低到67.45%,评价等级为“良”的相对增多,评价等级为“差”的电能表占2.13%。

3)投运时间为7年—9年的电能表中,状态评价等级为“优”的进一步降低到58.8%,评价等级为“一般”和“较差”的相对增多,评价等级为“差”的电能表占4.4%。

4)投运时间为10年以上的电能表中,由于近年技改项目的开展,更换了大部分性能较差的电能表,留下周期检验合格率较高的批次,且相应的备品备件充分,故在样本中没有评价等级为“差”的电能表,但“较差”的电能表比例也相对较多,评价等级为“优”的也仅有63.75%。

4.3 与传统评价方案的结果对比

用传统方案进行评价,即不剔除合理性较低的专家指标评分,直接确定指标权重。将传统方案所得结果与文中所提方案的结果进行比较,突出文中所提方案的有效性和优越性。

根据专家指标评分,使用传统方案计算的指标权重如表9所示。

表9 评价指标的权重

在传统方案获得的指标权重下,计算的评价结果按不同的电能表类型分类,结果如表10所示。

表10 评价结果按电能表类型划分

表10表明,电能表状态评价结果整体与表7接近,证明了文中所提方案的有效性。对比评价结果存在差异的电能表,发现评价结果基本仅差一个等级,影响不大;仅某一I类电能表,在传统方案下评价结果为一般,而在文中所提方案下,因周期检验合格率较低,评价结果为差,更符合状态评价要求,证明了文中所提方案的优越性。

5 电能表检修建议

随着电力设备产品质量的提高,电能表的运行可靠性和稳定性也在不断提高。完全根据现有规程对电能表进行周期性检验,可能造成物力和人力资源的浪费,此外,检验时带电作业的安全性和检修后的稳定性都会受到挑战。

有鉴于此,本节在电能表状态检验系统运用的基础上,结合每月电能表状态的评价结果和检修经验,给出一种检验策略建议:

1)对于I类电能表,因其重要性,仍需严格按照规程周期性检验。对于Ⅱ类电能表,在近两年周期性检验中仍为“优”时,可将一年一检的周期改为两年一检。对于等级为“优”或“良”的Ⅲ类电能表,且在近两年周期性检验中评价等级和评分稳定的,可以免去一次周期性检验,但是需要关注其运行状态的监测和评分的变化趋势。

2)对于评价等级为“一般”的电能表,需要关注其运行状态,严格按照规程周期性检验。若本月其评价等级不变,但是评分明显降低,应安排此类电能表下月进行临时检验;

3)对于评价等级为“较差”或“差”的电能表,应立即安排现场检验,及时分析其异常原因,并采取有关措施消除异常。若无法消除异常或评价仍为“差”的电能表,应及时更换,减少或避免因设备问题造成的损失。

4)对于投运年限大于10年的电能表,需要关注其运行状态的监测和评分的变化趋势,当评价等级下降或评分明显降低时,应及时安排进行现场检验。

6 结束语

文章提出了一种基于双重熵值修正指标赋权的电能表状态评价模型,并给出了灵活周期性检验策略,有着较好的应用价值。具体如下:

1)根据指标建立原则,梳理并构建了较为完备的电能表状态评价指标体系。

2)对传统熵值法进行了改进,提出了一种基于双重熵值修正指标权重的电能表状态评价方法。其基于相对熵修正专家的评分结果,提高了专家评分的合理性;并基于熵值修正G1法,减少了指标赋权的主观随意性。通过对比,突出了改进方法的有效性和优越性。

3)结合现场经验和电能表状态评价结果,给出了一种灵活的电能表检验策略建议,可以减少物力和人力消耗。