基于量子局部内在维度的对抗样本检测算法
张 瑜,昌 燕*,张仕斌
(1.成都信息工程大学 网络空间安全学院,成都 610225;2.先进密码技术与系统安全四川省重点实验室(成都信息工程大学),成都 610225)
0 引言
近年来,机器学习发展迅速,尤其是基于人工神经网络的深度学习逐渐渗透到人们生活中的各个领域,如图像识别[1]、信号处理[2]和优化组合[3]。金融背景下,股价预测[4]一直是人们持续关注的问题。由于受到市场因素以及其他不可控因素的影响,很难精准预测市场股价。研究人员提出使用深度神经网络(Deep Neural Network,DNN)预测每日股价的涨跌[5]。尽管在预测正常样本时有表现优异,但在实际应用中可能存在大量的攻击者恶意篡改股票数据,向原始数据中故意添加人眼无法观测的对抗扰动形成对抗样本,致使DNN 模型分类或预测出错,为用户提供错误的参考值。已有很多研究者在此基础上提出不同种类的对抗样本攻击方法生成对抗样本,如FGSM(Fast Gradient Sign Method)[6]、基于分类器的迭代线性化的DeepFool 算法[7]、基于雅可比矩阵的显著性图攻击(Jacobian-based Saliency Map Attack,JSMA)方法[8]、CW(Carlini &Wagner)攻击[9]等,对抗样本的输入使深度学习模型在置信水平极高的情况下作出错误判断,给深度学习的实际应用带来了巨大挑战。因此,研究深度学习模型的对抗样本防御方法尤为重要。
目前,对抗样本防御方法主要分为对抗攻击防御和对抗攻击检测两个方面:
1)对抗攻击防御是针对对抗样本攻击的防御方法,使深度学习模型在输入对抗样本时仍然保持良好的性能,提高了深度学习模型的鲁棒性。Goodfellow 等[10]为了使模型适应不同属性的样本集,提出对抗训练方法,将对抗样本与正常样本一同输入模型训练,提高模型的分类准确率;Athalye 等[11]分析了对抗样本生成方法的通用思想,提出了梯度掩码方法以隐藏模型原始的梯度信息,可有效规避基于梯度的攻击方法;Liao 等[12]将人眼无法察觉的对抗扰动视为噪声,设计高阶表征引导去噪器消除这些噪声,达到防御的效果;Papernot等[13]提出防御蒸馏方法,平滑训练得到蒸馏模型,提高模型的泛化能力,使模型在面对攻击时具备高弹性。
2)对抗攻击检测是指通过分析样本的对抗性,设计检测算法区分对抗样本。Xu 等[14]提出特征压缩方法,压缩不必要的输入特征,通过减小每个像素的颜色位深度和像素值的空间平滑,降低攻击的自由度,以DNN 预测的结果与原始样本预测结果的差值是否超过阈值的标准检测样本属性;Feinman 等[15]根据对抗样本与正常样本分布流形区域的不同,使用核密度估计(Kernel Density Estimate,KDE)和贝叶斯不确定性估计(Bayesian Uncertainty Estimate,BUE)检测低置信区域的数据点;Pang 等[16]使用逆交叉熵方法作为目标函数训练神经网络模型,通过设置的阈值策略识别检测对抗样本;Ma 等[17]分析了对抗性区域的特点,证明了基于不同密度的检测方法对于对抗性区域的定性具有局限性,提出使用局部内在维度(Local Intrinsic Dimensionality,LID)表征对抗性区域的内在维度,并将样本的LID 估计值作为分类检测器的评判依据,根据检测器输出的标签区分对抗样本,实验结果表明,基于LID 的检测方法在多种攻击策略下比KDE、BUE 等检测方法更具优势。
许多对抗攻击防御方法在面对多样化的攻击时仍存在一定的局限性。因为在面对更优化的对抗样本攻击时,已有的对抗攻击防御方法可能不再适用,因此,为解决深度学习模型预测股价时存在对抗样本攻击的问题,研究有效的防御方法十分必要。
在当今大数据时代,金融领域涌现海量数据。在面对股价预测、风险评估和投资组合等问题时,传统机器学习算法无法高效解决用户需求的问题。随着量子计算的发展,研究人员利用量子态的叠加性和纠缠性,将经典机器学习与量子计算结合,相继提出了量子傅里叶变换、Shor 分解大整数算法、Grover 搜索算法、量子相位估计(Quantum Phase Estimation,QPE)、量子主成分分析[18]和量子卷积神经网络[19]等学习模型,可实现经典算法的二次甚至指数级加速。
为解决深度学习模型预测股价时存在对抗样本攻击的问题,本文的工作重心集中于对抗样本的检测,将基于LID的对抗样本检测算法与量子计算结合,提出了基于量子LID的对抗样本检测算法。该算法充分利用量子计算的并行优势,使用量子算法计算待测样本的LID 估计值,避免了经典算法中的冗余计算,保证算法可用性的同时,降低了算法复杂度。使用鸢尾花数据集IRIS 和手写数据集MNIST 对本文算法进行实验验证,确保算法的可行性与有效性,并将它应用于金融领域,可有效检测深度学习模型在股价预测时存在的对抗样本;从理论上分析了本文算法的优势,同时给出了该算法的优化方向,结合对抗训练等对抗攻击防御方法,进一步提高预测模型的鲁棒性与准确性。
1 理论基础
1.1 量子态与量子比特门
在量子物理中,通常使用态向量描述一个系统的状态,与经典比特表示方法相比,单量子比特可以包含这两种标准正交基的信息,具体形式为:
其中:θ为变量,复矢量由正交基的线性组合描述,即两种可能性的叠加状态。复矢量系数满足归一化条件,能精准描述自然界中广泛存在的多重态粒子,也能使用不同的基态测量量子态携带的多种信息。在量子计算中,将量子门作用于量子比特上可改变量子比特的状态,如本文用到的Hadamard 门的矩阵形式可表示为:
1.2 振幅编码
将一个N维的经典向量x={x1,x2,…,xN}编码到n量子比特的振幅中,具体形式如下:
1.3 SWAP-Test
SWAP-Test 量子算法可求解两向量内积模的平方,用于衡量两个量子态之间的相似程度。量子线路如图1 所示。
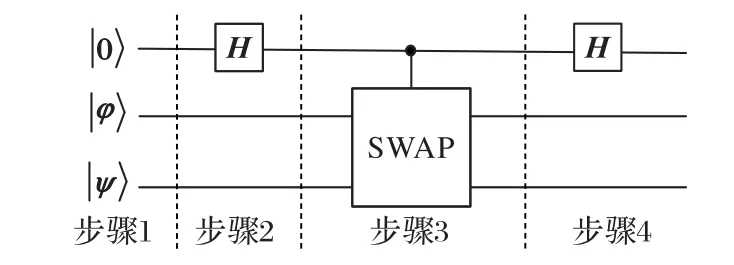
图1 SWAP-Test量子线路Fig.1 SWAP-Test quantum circuit
其中SWAP 门内部电路可细化为受控非门的组合,如图2 所示,左图为SWAP 门线路,等价于右图中受控非门的组合,本质上都是实现对两个量子比特的交换。
步骤4 辅助比特再次经过Hadamard 门,量子态的最终结果为:
2 基于LID的对抗样本检测算法
一个多分类DNN 模型通常包含输入层、隐藏层和输出层。在每层神经元的传递中都需经过含加权和偏置变量的转换函数f(w,b)以及激活函数σ的非线性映射,使DNN 模型能拟合更复杂的非线性函数。从图3 可以看出,输入向量为[x1,x2,…,xN]T,每层需经过含有权重矩阵Wk和偏置向量bk的线性函数(k为网络层层数(k∈[1,L])),并将结果传递至激活函数σk非线性映射,提取输入数据中更复杂的特征,最后输出所有类别的概率分布。由于每层网络中的神经元个数可能不一致,图中定义了第一层神经元个数为i,第二层神经元个数为i',第L-1 层神经元个数为j',最后一层进行j个类别分类。具体实现过程可简化为一个有向传递:
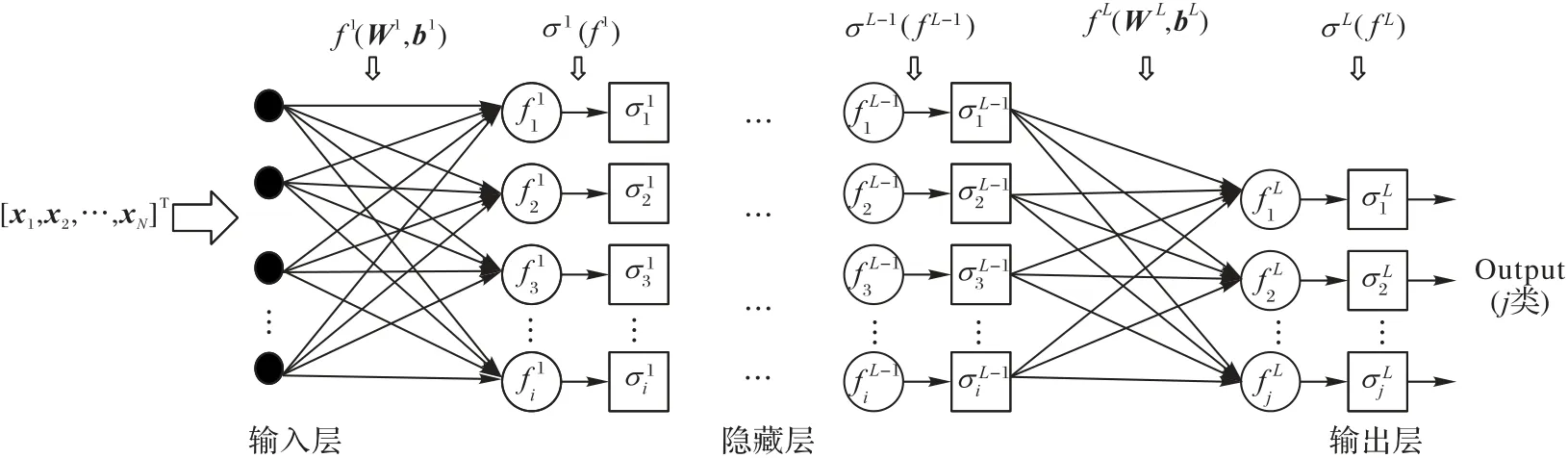
图3 多分类DNN模型Fig.3 Multi-classification DNN model
通过交叉熵损失函数作误差反向传播,进而训练模型、更新变量Wk和bk。多次迭代运行这一训练过程,直到损失值收敛,实现输入样本的多分类。
在深度学习模型的测试阶段,由于模型的脆弱性,敌手精心制作的对抗扰动很容易绕过隐藏层中冗余信息的过滤,将会遭受对抗样本攻击,导致模型输出异常。对抗性区域指对抗样本所在的区域,总是跨越一个连续的多维空间,接近对抗方向上的合法数据点,在保证一定攻击性的同时,又能逼近真实的样本数据。在此基础上,Ma 等[17]以输入层以及隐藏层的输出单元都有可能存在对抗扰动为出发点,并结合对抗性区域的特点,针对性地提出了基于LID 的对抗样本检测算法。本文将从该检测算法的原理、思路以及实验结论这3 个方面详细展开。
1)LID 是根据待测样本到邻近样本集的距离分布评估待测样本所在局部区域的空间填充能力。Amsaleg 等[20]提出使用LID 衡量样本局部区域的内在维度,设给定样本集X∼P,表示样本集X={x1,x2,…,xn}服从P 分布(广义帕累托分布),n为样本数。则样本x处的LID最大似然估计量公式:
其中:k为适度的邻近样本数,ri(x)表示当前样本与分布中第i个最近的样本之间的距离。
2)由于对抗样本总是跨越一个连续的多维空间,在高维数据的应用中,对抗样本的维度通常远大于任何给定的正常样本的维度,这意味着对抗样本的LID 估计值远大于正常样本的LID 估计值。在使用LID 衡量样本局部区域的内在维度特征基础之上,Ma 等[17]提出基于LID 的对抗样本检测算法,计算DNN 模型中每一网络层输出单元(激活值)的LID 估计值,构建一个以LID 为评判依据的检测器。
3)实验结果表明,对抗样本的LID 估计值显著高于正常样本的LID 估计值,即对抗性区域的内在维度更高,并且检测器成功分类的准确度高达99.5%。因此以样本局部区域的内在维度作为评判依据,可有效检测出对抗样本。
3 基于量子LID的对抗样本检测算法
本文为了实现高效的对抗样本检测算法,在基于LID 的对抗样本检测算法基础上,结合量子计算,提出基于量子LID 的对抗样本检测算法。本文算法充分利用量子态的并行优势,使用高效的量子算法代替反复迭代的经典算法。主要使用SWAP-Test 算法一次并行计算待测样本与所有样本之间的相似度;然后通过QPE 将相似度转换到量子比特上,利用量子Grover 算法搜索邻近k个样本以及保存对应的相似度,提高计算待测样本LID 估计值的效率。
本文将从量子态制备、计算待测样本LID 值以及训练二分类检测器等几个方面列出基于量子LID 的对抗样本检测算法的步骤。
1)量子态制备。
根据振幅编码规则,将待测样本与训练集样本的属性值归一化,得到待测样本x1=[x11,x12,…,x1N]T和所有但不包括x1的训练样本集Y=[Y1,Y2,…,YM]T,其中Yj=[Yj1,Yj2,…,YjN]T(j∈[1,M]),N代表每个样本的特征维数,M代表Y样本集中样本的数量,Yj表示样本集中第j个样本,向量元素YjN为样本归一化后的属性值。将编码的结果x1和Y作为量子算法的输入,分别制备为量子叠加态
2)计算待测样本LID 估计值。
使用Z基测量得到量子态第1个量子比特为1的概率因此经过测量后,式(12)的量子态坍缩为:
②通过QPE 算法,将测量出的相似度转换到量子比特上,可得到量子态
③使用量子Grover 算法搜索出最相似的k个样本集,并保存其对应的相似度。相似度从大到小排列,可表示为:max{d1(x1,Yind1),d2(x1,Yind2),…,dk(x1,Yindk) },其中indk为样本索引值。
④将相似度转换为余弦距离。本文基于余弦相似度与余弦距离关系的思想,相似度与余弦距离成反比关系,得出式(15):
其中:rt(x1)代表待测样本x1与第t个邻近样本Yindt的余弦距离。由于量子模拟器与运行次数shots等设置的不同,测量因子测出的概率幅值与传统计算存在一定误差,因此设置参数c调控距离。本文实验中取c=5。将相似度转换为余弦距离后,待测样本与邻近k个样本之间的距离从小到大可排列为min{r1(x1),r2(x1),…,rK(x1) }。
⑤代入式(9),求出待测样本x1的LID 值并保存。
3)计算所有待测样本LID 估计值。循环步骤1)、2),计算所有待测样本X={x1,x2,…,xs},s代表待测样本数,为有限正整数。直到计算并保存所有待测样本的LID 估计值后退出循环,保存结果为数组[LID1,LID2,…,LIDs]。
4)训练二分类检测器。为不同属性样本的LID 估计值添加不同的标签,比如对抗样本的LID 估计值设置标签为1,正常样本的LID 估计值设置标签为0。将数值和标签一同输入二分类检测器中监督学习,实现一个能准确分类对抗样本的检测器。
4 实验及理论分析
本章通过仿真实验详细展开以上算法步骤,具体步骤如图4 所示。首先制备量子态,使用振幅编码规则对待测样本xi和训练样本集Y编码;加载训练好的目标模型,并定义用于存储LID 估计值的列表、邻近样本数K以及参数c;然后在每层激活层中调用量子线路计算出xi与Y之间的相似度,选取出邻近K个样本点的相似度并转换为距离;再根据LID 公式就可以算出在当前层数中xi与Y之间的LID 估计值;最后将计算出的LID 估计值输入训练好的检测器中就可以检测出待测样本是否为对抗样本。仿真实验均在Google colab 平台实现,采用开源的跨平台python 库pennylane 开发程序,并调用cleverhans 库实施对抗样本攻击。

图4 基于量子LID的对抗样本检测算法程序实现Fig.4 Implementation of adversarial example detection algorithm based on quantum LID
为验证基于量子LID 的对抗样本检测算法的可行性与有效性,实验1 分别使用IRIS(4 维属性值)和MNIST(784 维属性值)两个数据集验证算法,均选择反向传播神经网络(Back Propagation Neural Network,BPNN)作为目标模型、对抗扰动系数δ=0.1 的FGSM 作为对抗样本攻击算法;为解决目标模型对股价预测时存在对抗样本攻击的问题,实验2将本文算法应用到股票时序数据(浦发银行股票的历史数据),并使用长短期记忆(Long Short-Term Memory,LSTM)网络作为目标模型、对抗扰动系数δ=0.1 的FGSM 作为对抗样本攻击算法。结合仿真实验的结果,理论分析本文算法的优势。与基于LID 的对抗样本检测算法相比,本文算法降低了时间复杂度,能高效检测金融背景下股票数据存在的对抗样本,进而达到对抗防御的目的。
4.1 仿真实验
1)有效性验证。
①首先使用120 条IRIS 鸢尾花数据训练目标模型BPNN(含5 层全连接层),其中每个样本包含4 维特征:花萼长度、花萼宽度、花瓣长度和花瓣宽度。然后输入30 条鸢尾花测试集测验,最终目标模型的分类准确率高达99.9%。为模拟对抗样本攻击,使用FGSM 对抗样本攻击算法(对抗扰动系数δ=0.1)生成30 个测试样本的对抗样本集,输入目标模型BPNN 分类时,准确度降至56.6%。为验证本文算法的可行性与有效性,使用经典检测计算方法和本文算法比对分析。图5 是分别使用经典LID 和量子LID 计算方法求出待测样本xnorm和对应对抗样本xadv在经过目标模型隐藏层(3 层)后该样本激活值的LID 估计值,其中,纵坐标LID 表示使用经典LID 计算方法计算出的数值,LIDq代表使用量子LID 算法计算的数值。可以看出,量子LID 计算方法同样能有效计算出正常样本与对抗样本的内在维度,与经典计算方法效用相当,均验证了对抗样本与正常样本的LID 估计值有明显差异,对抗样本的LID 估计值显著高于正常样本的LID 估计值。因此,以量子LID 算法计算出的LID 估计值作为二分类检测器的评判依据,可有效区分对抗样本,达到对抗防御的目的。
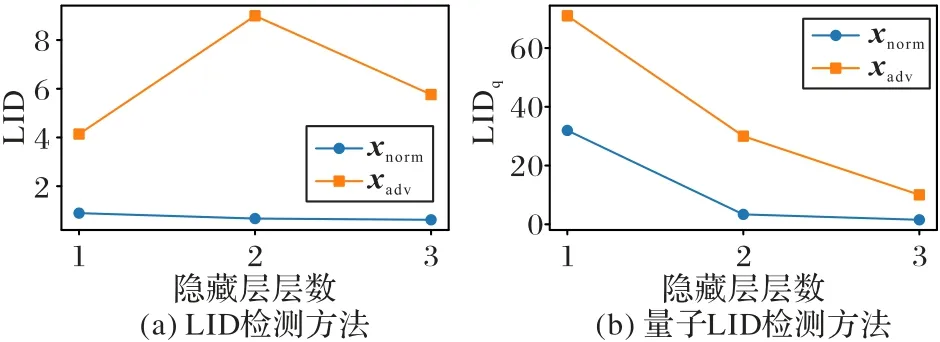
图5 使用经典LID和量子LID算法计算IRIS数据样本LID值的实验结果对比Fig.5 Experimental result comparison of calculating LID values of IRIS data examples by classical LID and quantum LID algorithms
②使用高维手写数据集MNIST 对本文算法进行实验,其中数据集包括60 000 条训练数据和10 000 条测试数据,迭代训练100 次,得到准确度为98.0%的目标模型BPNN。同样采取FGSM 攻击算法,在原始样本中故意添加扰动系数δ为0.1 的噪声,从而实施对抗样本攻击。攻击效果如图6(b)所示,目标模型对于对抗样本均分类出错,如第一个对抗样本的信息7→3 表示真实标签为7,却被目标模型分类为3。因此,为检测出对抗样本,引入本文算法作样本检测。在向目标模型输入待分类样本后,使用量子LID 计算方法对样本每一网络层激活值求出LID 估计值。图6 中的LID 值指使用量子LID 算法求出待测样本在经过目标模型最后一网络层后该样本激活值的LID 估计值。从实验结果可知,大部分对抗样本的LID 估计值均显著高于正常样本的LID 估计值,表明对抗样本的内在维度普遍高于正常样本,结果与预期设想一致。计算的LID 估计值可以体现对抗样本和正常样本之间的差异性,LID 估计值大的样本为对抗样本,反之为正常样本。因此,使用量子LID 算法计算出的LID 估计值作为检测对抗样本的评判依据,并为它加上对应的标签,将数据与标签一同输入二分类检测器,可实现对抗样本的有效检测。

图6 使用量子LID算法计算MNIST数据样本LID值的实验结果Fig.6 Experimental results of calculating LID values of MNIST data examples by quantum LID algorithm
2)实用性验证。
将提出的基于量子LID 的对抗样本检测算法应用于金融领域,期望能有效检测出股票数据集中存在的对抗样本,解决深度学习模型预测股价时存在对抗样本攻击的问题。
实验中选取浦发银行股票的历史数据作为数据集,其中每天的股价由多种特征决定,本文提取出4 种特征(开盘价open、最高价high、最低价low 和闭盘价close)。每一个样本数据包含前20 d 的特征,且以第21 d 的闭盘价作为标签。首先使用1 500 条样本数据迭代训练目标模型LSTM 200 次,最终的损失值逐渐收敛到0 左右;然后同样使用对抗扰动系数δ=0.1 的FGSM 攻击算法,为200 条测试数据添加对抗扰动生成对应的对抗样本集,再根据量子LID 算法计算各样本的LID 估计值。本文选取了其中3 个正常样本以及对应对抗样本的LID 估计值,如表1 所示。可以看到将本文算法应用于时序数据时,仍然可得出结论:对抗样本的LID 估计值显著高于对应正常样本的LID 估计值,即LID 估计值大的样本为对抗样本,反之为正常样本。因此,依据量子LID 算法计算的LID 估计值作为检测对抗样本的评判依据,输入训练好的二分类检测器中能有效检测出对抗样本。实验结果表明,在量子金融背景下,敌手向金融时序数据添加对抗扰动生成对抗样本时,仍能通过本文算法检测。

表1 使用量子LID算法计算股票数据样本LID值的实验结果Tab.1 Experimental results of calculating LID values of stock data examples by quantum LID algorithm
4.2 理论分析
以上仿真实验结果验证了算法的可用性与有效性。接下来将从理论层面分析基于量子LID 的对抗样本检测算法的优势。
本文算法利用了量子优势,充分发挥量子并行性,能一次性处理大批量数据集,避免了经典算法中的冗余计算,提高了计算效率。本文算法在制备量子态并计算一次SWAPTest 交换门后,利用相位估计算法思想,迭代R次Grover 算子将相似度信息转存到量子态上,其中R与相位估计的准确率有关;向M个训练样本中搜索K个相似度最大的样本点需要执行次迭代操作,可得出本文算法的时间复杂度为然而,基于经典LID 的对抗样本检测算法需要反复迭代部分算法,如计算待测样本与M个训练样本的距离需要的时间复杂度为O(M)、并向其中搜索邻近的K个样本点需迭代运行O(KM)次,即基于LID 的对抗样本检测算法的时间复杂度为O(KM2)。因此,基于量子LID 的对抗样本检测算法相较于经典算法更高效,降低了时间复杂度,实现了指数级加速。
5 结语
本文将量子计算与基于LID 的对抗样本检测算法结合,提出基于量子LID 的对抗样本检测算法。所提算法充分利用量子并行的优势,使用量子算法计算待测样本的LID 估计值,避免了经典算法中的冗余计算。在仿真实验中,使用IRIS 和MNIST 数据集验证了所提算法的可行性与有效性,并将算法应用到股价预测中,同样可以根据计算的LID 估计值检测对抗样本。理论分析表明,基于量子LID 的对抗样本检测算法比基于LID 的对抗样本检测算法更高效,降低了算法的时间复杂度,实现了指数级加速。
由于对抗样本检测独立于对抗样本防御方法,可结合对抗训练等方法进一步提高目标模型的鲁棒性与准确性。此外,当用户数据量较大且需求更高时,对该算法优化十分有意义,并且在中等规模含噪量子时代下,量子优势可能会更容易实现,使得本文算法应用于对抗样本检测任务成为可能。

