基于路径模仿和SAC强化学习的机械臂路径规划算法

宋紫阳，李军怀，2，王怀军，2*，苏 鑫，于 蕾，2

（1.西安理工大学 计算机科学与工程学院，西安 710048；2.陕西省网络计算与安全技术重点实验室，西安 710048）

0 引言

工业机器人的规模化应用提高了工业和制造业等行业的生产效率。机械臂是机器人的主要形式之一，通过运动副的转动或移动使机械臂末端运动到合适的位置和姿态，完成不同的工作任务。机械臂具有较高的自由度，能部署在不同场景下，快速执行作业任务。机器学习（Machine Learning）技术可以提高机器人的智能化水平，让机器人拥有自主决策与学习能力，在机器人轨迹路径规划［1-2］、环境感知［3-4］和智能决策与控制［5-6］等方向都有应用。强化学习克服了传统机械臂控制方法对环境状态变化适应能力差的缺点，成为机械臂智能化研究的重要方向［7-8］。

目前，基于强化学习的机械臂路径规划面临两个问题：1）机械臂的动作维度高、环境状态复杂，强化学习面对海量的状态数量和动作数量较难进行价值评估；2）奖励稀疏的问题，即当机械臂到达指定位置时才能得到奖励，导致训练时间长，效果较差。

在基于强化学习的机械臂路径或轨迹规划等方面，国内外学者已经有了一定的研究成果。

基于深度强化学习（Deep Reinforcement Learning，DRL）的机械臂路径规划。DRL 使用深度神经网络（Deep Neural Network，DNN）近似价值函数或策略函数，较好地解决了环境状态与动作维度高、数量庞大，数据特征难以在有限的计算机内存中存储、计算和表达等问题。谷歌公司的DeepMind 团队［9］改进了DQN（Deep Q-Network）方法，提出了具有竞争网络结构的DQN 方法（Dueling DQN），提高了DNN对价值函数拟合的准确性，但在面对连续控制问题时无法得到最优控制策略。Gu 等［10］提出归一化优势函数（Normalized Advantage Functions，NAF）方法，在DQN 的基础上拓展了对连续控制问题的支持。Prianto 等［11］为了解决高维路径规划问题，提出了基于SAC（Soft Actor-Critic）的路径规划算法，为了有效处理构型空间中的多臂问题，扩充了各臂的构型空间，采用后见经验重放（Hindsight Experience Replay，HER）方法提高样本效率，可以实时、快速地生成任意起始点和目标点的最短路径。本文在文献［11］的基础上，设计特殊的奖励函数指导智能体学习如何选择最优行为，进一步扩展SAC强化学习的Critic 部分，采用两个Q 网络和两个目标Q 网络对机械臂的路径规划设计进行优化，以达到更快速强化学习的目的。张永梅等［12］基于DRL 算法对连续型动作输出的端到端机器人路径规划进行研究，提出了内在好奇心驱动的深度确定性策略梯度算法，实现了端到端的机器人路径规划，有利于解决训练前期奖励难获取问题。

自从模仿学习被提出，它已被应用于机械臂路径规划。模仿学习被用于结合深度学习训练机械臂路径控制模型，或与强化学习结合训练得到路径规划的最优策略。于建均等［13］通过拖动机械臂的方式得到示教路径，基于模仿学习和DNN 实现机械臂对示教路径的快速学习，解决了机械臂动作规划编程复杂的问题。Rahmatizadeh 等［14］结合了长短期记忆（Long Short-Term Memory，LSTM）网络和混合密度网络（Mixture Density Network，MDN）作为机械臂的控制器，基于深度相机Kinect 获取示教路径，通过模仿学习使机械臂合理规划路径完成物品的拾取和放置。加州大学Finn 等［15］使用逆最优控制（Inverse Optimal Control，IOC）训练机械臂路径规划，通过优化奖励函数引导价值对示教路径进行模仿学习，使机械臂学会了合理规划路径摆放盘子。使用示教路径优化奖励函数可以对智能体在训练过程中策略输出的动作作出更好的评价。汤自林等［16］基于模仿学习提出了变刚度协作搬运控制策略，使用任务参数化的高斯混合模型（Task Parameterized Gaussian Mixture Model，TP-GMM）对示教路径编码，学习不同搬运工况下的搬运轨迹概率模型，提高了特定搬运任务的终点位置精度。

合理的机械臂运动路径是机械臂系统实现运动控制功能和完成任务的基础，本文提出一种基于路径模仿和SAC 强化学习的机械臂路径规划算法。通过将机械臂末端的示教路径和实际路径融入奖励函数，使机械臂在强化学习过程中模仿示教路径纠正实际路径，提高学习效率，选择SAC 算法作为强化学习方法使训练收敛更快且更稳定。

1 机械臂路径规划基本原理

针对强化学习在机械臂路径规划中奖励稀疏难以收敛的问题，引入对参考路径的模仿学习，根据机械臂运行的实际路径与参考路径的差异设计适当的奖励方式，实现快速强化学习的目的。基于模仿学习的机械臂运动控制方法可分为示教路径的获取和示教路径的学习两个阶段。将手拖动机械臂所检测到的手部路径作为示教路径，在人拖动机械臂的过程中，机械臂通过编码器获取关节角度后通过正运动学方法解出机械臂的末端路径，将末端路径作为示教对象。基于SAC 强化学习的机械臂路径规划算法原理如图1 所示。

图1 机械臂路径规划算法原理Fig.1 Principle of manipulator path planning algorithm

SAC 算法基于Actor-Critic 框架，使用了5 个DNN 和1 个经验回放池完成强化学习任务。5 个DNN 分为两组：一组包含一个策略网络，是SAC 强化学习算法的Actor 部分；另一组包含两个Q 网络和两个目标Q 网络，是SAC 强化学习的Critic 部分。奖励函数根据实际路径和参考路径的距离来计算奖励或者惩罚。SAC 算法将机械臂状态和奖励函数的输出作为输入，向机械臂反馈下一步的动作。

2 路径模仿的奖励函数计算方法

机械臂SmallRobotArm 选择六自由度，机械臂末端连接一个电磁铁。设定机械臂路径规划任务为拾取硬币并将硬币置入杯中。奖励函数根据机械臂的当前状态st和下一步要执行的动作at计算机械臂的任务完成度，根据任务完成度和机械臂末端与参考路径的距离计算奖励或者惩罚，诱导机械臂学习参考路径。

1）机械臂状态模型。

在机械臂路径规划任务背景下定义环境状态，t时刻的状态st∈S是一个四元组：st=(post，quatt，c，w)，其中post表示t时刻时机械臂末端 在空间中的位 置：post=(xt，ypt，zpt)，quatt表示机械臂末端效应器在空间中的姿态角：quatt=(wqt，xqt，yqt，zqt)，c表示硬币在空间中的位置，w表示水杯在空间中的位置。

2）机械臂动作模型。

机械臂的动作at∈A由 3 个部分构成 ：at=(ΔPt，ΔOt，gt)，ΔPt和ΔOt的表达式分别为ΔPt=(Δxpt，Δypt，Δzpt)，ΔOt=(Δxot，Δyot，Δzot)，其中ΔPt表示机械臂末端在t时刻移动位移的向量，ΔOt表示机械臂末端在t时刻的转动姿态角，gt表示机械臂末端的电磁铁在t时刻是否接通了电源。

3）奖励函数模型。

奖励函数反映了在状态st下进行动作at的奖励的预期，可表示为：

由于系统状态空间大，很难为所有状态设置奖励，奖励稀疏的问题导致学习缓慢甚至无法学习。为了使机械臂能快速学习针对任务的最优路径，通过特殊设计的奖励函数使机械臂对参考路径模仿学习，提高机械臂路径规划的学习速度和任务执行成功率。

将用手拖动机械臂获得的末端路径作为机械臂学习的参考路径，参考路径如图1 所示。

定义机械臂在t时刻的任务完成度为pt：

根据任务要求，奖励或惩罚可分成3 种情况：

①若机械臂完成将硬币置入水杯中的任务可得到最大奖励；未完成任务时不奖励。

②当机械臂末端沿着参考路径的方向运动时得到奖励；当机械臂沿着参考路径的反方向运动时奖励值为负，即受到惩罚。

③机械臂末端与参考路径的距离越近受到奖励越大；距离过远则会受到惩罚，距离越远惩罚越大。

根据上述分析，执行动作at后的奖励为：

其中：Δd表示机械臂末端位置与参考路径之间的距离；β为控制机械臂末端偏离参考路径时受到奖励或惩罚的比例系数；η为参考路径奖励半径，当机械臂末端在η内时会得到奖励，否则会受到惩罚。

在强化学习中，这种奖励机制可以诱导机械臂学习参考路径，使策略更快收敛，提高学习效率。

3 机械臂路径规划算法

SAC 是一种基于Actor-Critic 无模型强化学习框架，它融合了最大熵思想，在获得高回报的同时，也具有较强的探索能力和较高的鲁棒性［17］。结合奖励算法和SAC 强化学习方法，可以用奖励函数指导智能体学习如何选择最优行为，同时使用SAC 训练智能体，使它根据定义的奖励函数和状态选择合适的动作。通过设计合适的奖励函数，智能体可以学习如何选择最优路径，使得机器人准确到达目标点。

综上所述，将奖励算法和SAC 强化学习算法结合，可以构建一种新的路径规划算法，使得机器人能够根据环境状态动态地选择最优路径，具有较高的适应性和鲁棒性。

3.1 最大熵策略

SAC 强化学习算法可以探索更多情况，以提高学习速度，且避免陷入局部最优解，在获得的最大回报和随机性探索之间寻找一种平衡，使策略可以兼顾预期回报与最大熵。在SAC 中，最优策略表示为：

其中：R是奖励；H为熵；E 表示求奖励和熵的期望；α是温度系数，决定了熵值相较于奖励的比重，调整α可以控制最优策略的探索随机性。H的计算式为：

熵值的大小反映了策略π(⋅|st)的随机程度，在熵较大时，机械臂在价值相近的动作中随机选取一个执行。

在SAC 算法中，最大熵是策略的目标之一，因此用于表示预期回报的V 函数和Q 函数中的熵是奖励的一部分，被称为软性状态价值函数（软性V 函数）和软性动作价值函数（软性Q 函数）［18］，分别表示为：

软性Q 函数的贝尔曼方程形式表示为：

软性Q 函数和软性V 函数的更新式为：

通过对式（9）～（10）不断迭代，Q 函数的输出将逐渐收敛至最优Q值。

3.2 基于能量模型的策略

SAC 算法对AC 策略的更新方式进行了改进。在SAC 算法训练的过程中，策略向着软性Q 函数的指数方向更新：

在强化学习场景下，软性Q 函数若是多峰，则代表问题的解不唯一。面对有多个最优解或存在次优解时，基于能量模型的策略分布使算法可对所有可行的解进行学习。当环境发生变化，之前的最优解行不通时，基于能量模型的策略分布可以迅速调整策略得到新的解。对于SAC 算法，最优策略的形式如下：

3.3 SAC强化学习算法

本文引入两个结构相同的Q 网络同时训练，每次迭代时选择较小的Q 值更新策略网络，防止对动作价值估计过高［19］。Target-Q 网络在每次迭代中进行软更新，网络参数的变化较为平缓。使用第2 章所述的基于路径模仿的奖励函数，诱导机械臂学习参考路径。

本文算法的框架如图2 所示。策略网络将来自环境的状态s作为输入，有13 个参数，输出动作a，共8 个参数，隐藏层是5 个全连接层，每层512 个神经元，使用Leaky ReLU［20］和Tanh 分别作为隐藏层和输出层的激活函数。

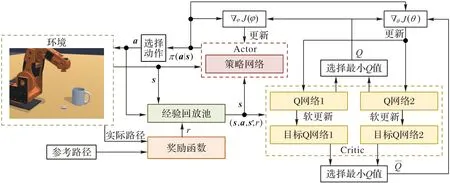
图2 本文算法的框架Fig.2 Framework of proposed algorithm

设策略网络参数为φ，损失函数为：

其中：D表示经验回放池，奖励函数根据任务完成度和机械臂末端与参考路径的距离计算出奖励，并且存到经验回放池，经验回放池将状态、转换后的状态、动作和奖励(st，at，st+1，Rt+1)作为Q 网络训练的数据来源。α为温度参数，随着状态的变化而自动调节，面对探索过的环境状态，应当减小温度参数令熵减小，而面对未知状态应当增大温度参数，增强策略探索的随机性。温度参数α自动调节过程可表示为：

4 个Q 网络结构完全相同，它们的输入为状态s和策略网络输出的动作a，共21 个参数，输出单个参数即Q 值，隐藏层为3 个全连接层，每层512 个神经元，使用Leaky ReLU 作为激活函数。设Q 网络的参数为θ，损失函数：

其中：τ值大于0 但远小于1。

SAC 算法的伪代码如算法1 所示。

算法1 SAC 算法。

4 实验与结果分析

本章通过实验展示本文算法的实际效果，验证该算法在解决实际任务问题中的可行性，通过对比实验验证该算法相较于深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG）强化学习算法［21］训练速度更快且成功率更高。

4.1 实验环境

强化学习环境基于Unity ML-Agents 工具包搭建，使用Python 实现强化学习算法，使用TensorFlow 构建深度网络。

实验场景如图3 所示，机械臂放置在桌面上，机械臂前方摆放一个硬币和一个杯子，首先机械臂末端移动到硬币上方，通过电磁铁将硬币拾起，再将硬币置入杯子中。

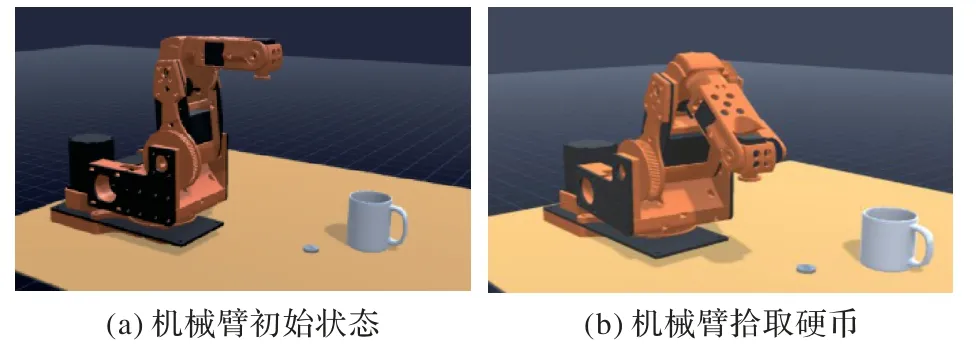
图3 机械臂路径规划训练场景Fig.3 Training scene of manipulator path planning

4.2 实验结果与分析

为验证本文算法的训练速度和效果，另外设置一组路径模仿算法作为对比。将通过用手拖动机械臂得到的路径作为参考路径。两种算法如下：

本文算法基于路径模仿和SAC 算法。奖励函数如第2章所述，智能体所受到的奖励和惩罚与是否完成任务以及对参考路径的学习程度有关，SAC 强化学习算法能较好地对环境进行探索，提高学习速度。

基于路径模仿和DDPG 算法。DDPG 算法与SAC 算法同属于Actor-Critic 框架，不同的是DDPG 算法是直接选取概率最大的动作去执行。DDPG 算法包含4 个神经网络：策略网络、目标策略网络、Q 网络和目标Q 网络，这些网络的结构与SAC 算法中对应网络结构一致。

对上述两种算法各训练1 000 回合，每个训练回合机械臂最多执行100 次动作，若达到100 次动作后仍无法完成任务则恢复初始状态，开始下一轮训练。统计两种算法在每个训练回合的累积奖励，绘制相应的曲线如图4 所示。

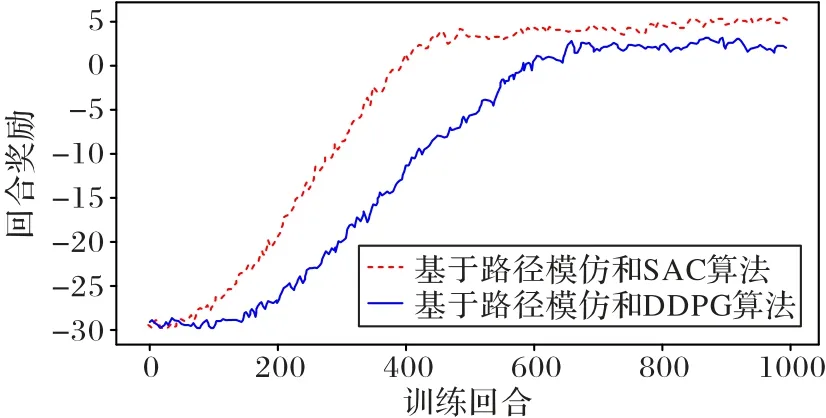
图4 两种算法的奖励变化曲线Fig.4 Reward change curves for two algorithms

从图4 可以看出，两种算法在开始训练时机械臂得到的奖励都比较低，为-30 左右。随着训练次数的增加，基于路径模仿和SAC 算法的奖励在不断上升，400 回合之后奖励值稳定在15 左右。基于路径模仿和DDPG 算法的奖励增长曲线滞后于本文算法，在训练到200 回合之后开始增长，在600回合左右时奖励值稳定在12 左右。

每训练40 回合统计一次任务成功率，两种算法训练1 000 回合的任务成功率曲线如图5 所示。

图5 两种算法的成功率变化曲线Fig.5 Change curves of success rate for two algorithms

从图5 可以看出，成功率曲线与奖励曲线的趋势基本一致，两种算法在训练刚开始时成功率都很低，随着训练回合增多，成功率逐渐增高，基于路径模仿和SAC 算法在第400回合左右成功率稳定在88%左右，而基于路径模仿和DDPG算法在600 回合左右时成功率稳定在88%左右。

机械臂基于两种算法分别规划10 条路径，统计两种算法所规划路径的平均长度以及与参考路径的距离差，统计结果如表1 所示。

表1 10条路径的路径规划实验结果 单位：cmTab.1 Experimental results of path planning for ten paths unit：cm

机械臂基于路径模仿和SAC 算法和基于路径模仿和DDPG 算法规划的路径与参考路径的对比如图6、7 所示。

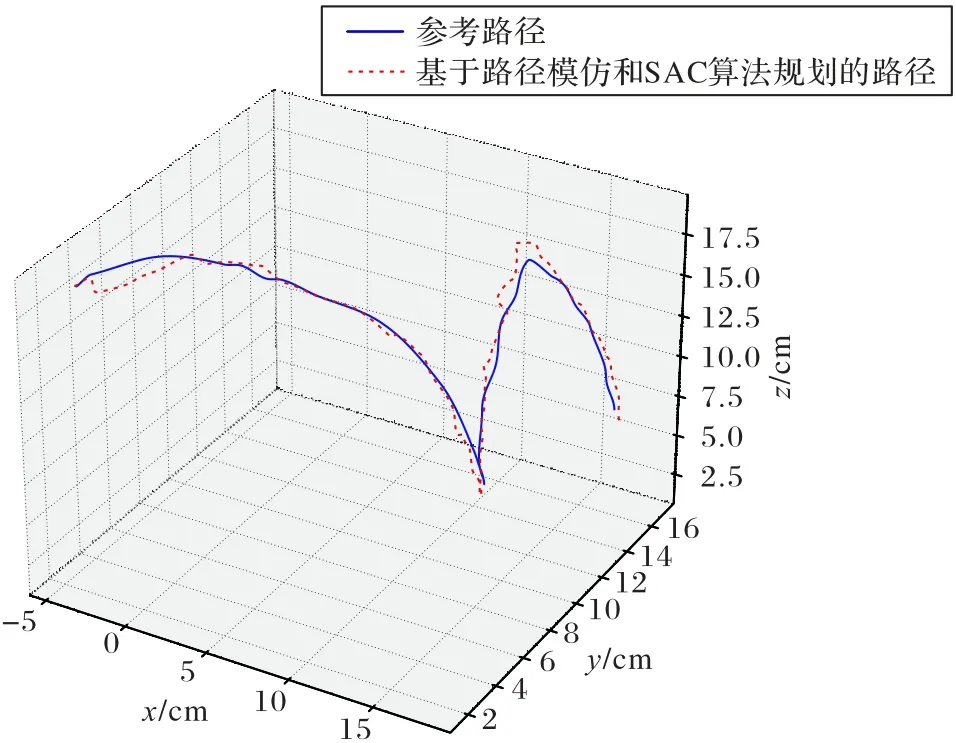
图6 参考路径及基于路径模仿和SAC算法规划的路径对比Fig.6 Comparison between reference path and path based on path imitation and SAC algorithm

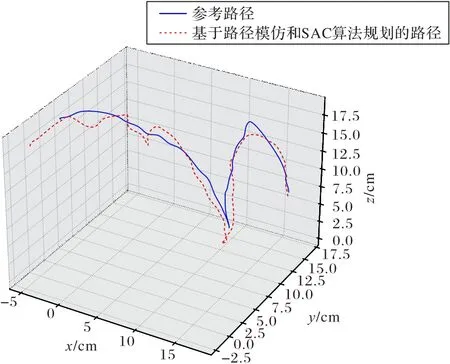
图7 参考路径和基于路径模仿和DDPG算法规划的路径对比Fig.7 Comparison between reference path and path based on path imitation and DDPG algorithm

为验证基于路径模仿和SAC 的算法对不同路径的学习效果，采集一条不同的机械臂运动路径作为参考路径令机械臂学习，令机械臂规划一条运动路径完成实验任务。基于SAC 方法的路径规划算法所规划的路径和参考路径的对比如图8 所示，基于SAC 方法的路径规划算法规划的路径长度为58.4 cm，偏离参考路径的最大距离为1.8 cm，偏离参考路径的平均距离为0.9 cm，机械臂针对不同的参考路径都能学习并规划合理的路径来完成任务。

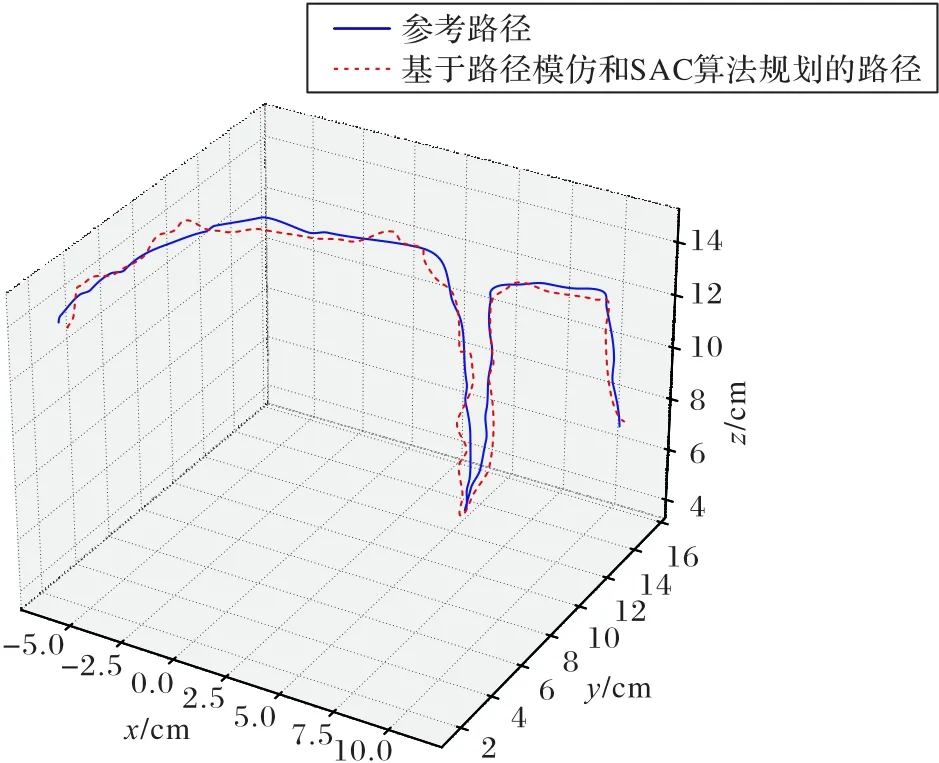
图8 不同的参考路径及基于路径模仿和SAC算法规划的路径对比Fig.8 Comparison of different reference path and path based on path imitation and SAC algorithm

5 结语

针对目前机械臂强化学习存在奖励稀疏导致的收敛速度慢的问题，本文提出一种基于路径模仿和SAC 强化学习的机械臂路径规划算法。首先对基于路径模仿和SAC 强化学习的机械臂路径规划算法的基本原理进行描述；其次介绍了基于路径模仿的奖励函数设计原理；接着对SAC 强化学习算法进行了介绍，给出了算法流程；最后进行了机械臂路径规划对比实验，实验结果表明本文算法能够有效训练机械臂完成硬币投掷入杯的任务，路径模仿机制解决了强化学习的训练中奖励稀疏难以训练的问题，SAC 算法相较于DDPG 算法探索能力更强，所规划的路径更加合理。