基于最大熵深度强化学习的双足机器人步态控制方法

李源潮，陶重犇，2*，王 琛

（1.苏州科技大学 电子与信息工程学院，江苏 苏州 215009；2.清华大学 苏州汽车研究院，江苏 苏州 215134）

0 引言

双足机器人属于仿人机器人。相较于轮式、履带式机器人，双足机器人具有复杂的腿部关节结构，不仅可以获得更高的灵活度与适应性，而且能实现爬楼梯、非平整地面等复杂路面情况下的正常行走［1］。因此获得快速、稳定的步态控制是双足机器人的研究重点［2］。由于非线性和不稳定性因素，双足机器人步态控制系统的设计比较困难［3］。传统基于模型的步态控制已有大量研究［4-7］。针对特定的步态运动，通常采用开环控制方法预先设定各关节的位置轨迹，控制各关节位置，以实现运动。基于零力矩点（Zero Moment Point，ZMP）的方法是双足机器人步态控制的常用方法［8-9］。这些传统的方法依赖于复杂的动力学模型和数学工程，但是在自身和环境变化时，容易造成运动失效［10］。

传统基于模型的步态控制方法很难适应多变的环境。相比之下，由于自适应学习的特性，端到端的深度强化学习（Deep Reinforcement Learning，DRL）算法越来越多地应用于机器人控制领域。端到端DRL 可以不假设任何步态或机器人动力学的先验知识，应用于机器人系统［11］。如果成功应用，DRL 可以自动完成对控制器的设计。而基于模型的方法由于环境动力学模型复杂，无法得到准确的模型，给智能体训练产生了误差。无模型的方法无需构建环境模型，智能体直接与环境交互，它的策略更准确，对环境的适应性更好［12］。

本文提出一种基于最大熵深度强化学习方法对双足机器人的步态控制方法，采用最大熵框架，可以让策略尽可能随机。双足机器人可以更充分地探索状态空间，避免策略过早落入局部最优点，充分发挥双足机器人自主探索的能力［13］，获得适应环境的步态，提高抗干扰能力。本文的主要工作如下：

1）针对双足机器人连续直线行走的步态稳定控制问题，提出一种基于柔性演员-评论家（Soft Actor-Critic，SAC）的DRL 步态控制方法。该方法无需事先建立动力学模型，使双足机器人直接与环境交互，获取经验样本优化策略函数。并且输入神经网络的参数来自机器人本身的关节角度，无需额外的传感器，从而使该方法具有更好的移植性。

2）针对DRL 样本效率低下，导致策略收敛缓慢的问题，提出了一种余弦相似度方法对经验样本分类，提高样本使用效率，并且加快了训练的收敛。

3）针对双足机器人受髋关节摆动影响无法较好地实现直线行走的问题，利用知识和经验设计奖励函数，约束双足机器人直线行走。

1 相关工作

在过去30 年里，许多学者使用不同的方案控制双足机器人的步态，从基于模型的传统控制方法到端到端的DRL方法；然而，设计机器人模型所需的专业知识以及精确的机器人动力学模型很难获得。相反，无模型的DRL 方法无需环境动力学模型，机器人直接与环境进行交互，同时在和环境交互不断试错的过程中，观察环境相关信息并利用反馈的奖励信号不断学习，寻找最优策略。

双足步行控制可以被抽象为解决未处理的高维感官输入复杂任务的一种方式。深度学习（Deep Learning，DL）已在解决高维复杂问题方面取得了许多成就。DRL 将DL 和强化学习（Reinforcement Learning，RL）相结合，既具有解决高维复杂问题的能力，也具有决策能力。Actor-Critic 框架法结合了价值函数和策略函数，解决了策略函数法收敛速度慢的问题。例如深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG）算法［14］和异步参与者批评家（Asynchronous Advantage Actor-Critic，A3C）［15］算法。A3C 算法通常获得局部最优解，对策略的评估效率低下。Wu 等［16］引入了DRL 算法，为传统步态控制方法解决了上述问题。DDPG 算法、近端策略优化（Proximal Policy Optimization，PPO）算法［17］和信赖域策略优化（Trust Region Policy Optimization，TRPO）算法［18］可以探索连续的动作空间，使深度强化学习算法成功应用于双足机器人的步态控制问题［19］。赵玉婷等［20］将深度Q 学习（Deep Q-Network，DQN）算法应用于双足机器人在非平整地面的步态控制，在V-Rep 平台经过多回合训练调整实现稳定的双足机器人行走。Tao 等［21］将一种并行DDPG 算法用于双足机器人步态控制，改进了经验回放机制，提高了采样效率和优化了策略函数，并在RoboCup 仿真环境中实现了稳定行走。Rodriguez 等［22］将深度强化学习算法用于双足机器人全向行走控制。每一个运动是由单个控制策略网络实现的，目标难度逐步增加，最终实现双足机器人全向行走。

虽然DRL 算法在处理复杂的双足机器人步态控制问题方面具有优势，但仍会陷入探索困境。由于缺乏对环境的鲁棒性，整体收益小，导致双足机器人行走效果较差等。最大熵DRL 算法基于最大熵原理，旨在通过加权最大化期望收益和策略的期望熵。产生相对稳健的策略是最大熵强化学习的一个优点，由于在训练期间注入结构化噪声，使策略更广泛地探索状态空间，可以有效提高策略的鲁棒性［23］。该算法直接让双足机器人与环境进行交互，并使用自身采样的样本数据提高策略性能，使它更好地适应环境。本文方法还优化经验回放机制，使用余弦相似度对经验分类，提高采样效率；同时，还设计了一系列奖励机制，以提高双足机器人行走稳定性。本文的步态控制方法框架如图1 所示。

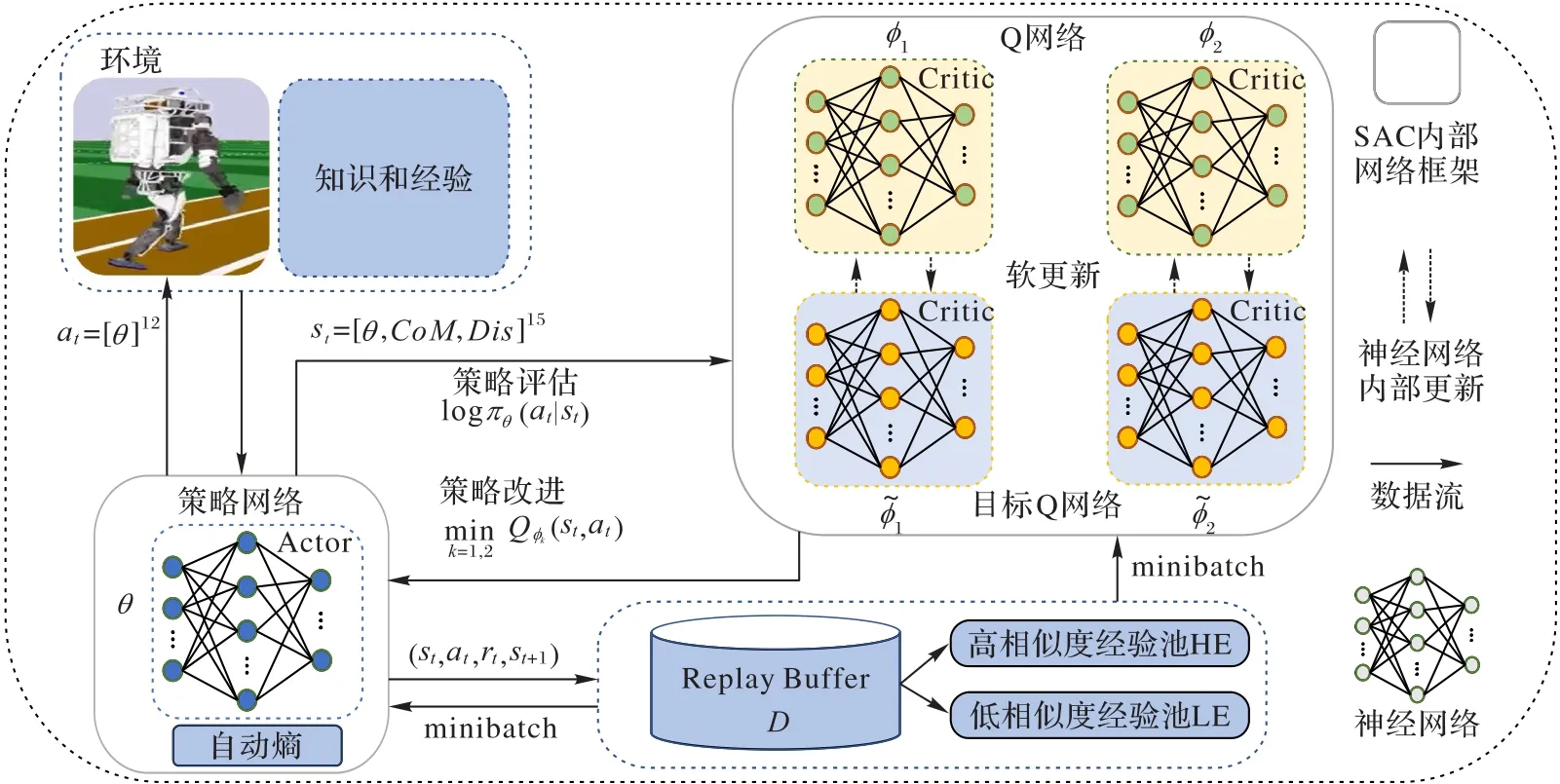
图1 本文步态控制方法的总体框架Fig.1 Overall framework of the proposed gait control method

2 基于柔性演员-评论家的步态控制方法

2.1 深度强化学习

深度强化学习是通过智能体与环境交互学习。智能体选择一个动作后，会从环境中得到相应的状态和奖励。通过这个持续交互过程的学习，最终获得最优策略函数。智能体与环境之间的交互被建模为马尔可夫决策过程（Markov Decision Process，MDP）。MDP 通常由一个五元组表示(S，A，P，R，γ)，其中：S表示状态集合；A表示可执行的动作集合；P：S×A×S→[0，1]表示状态转移函数；P(st+1|st，at)表示智能体在状态st下采取行动at后转移到下一个状态st+1的概率；R：S×A×S→R表示奖励函数；R：(st，at，st+1)表示智能体在状态st下采取行动at后转移到下一个状态st+1的立即奖赏；γ是奖励的折扣系数。智能体通过选择使未来奖励最大化的动作与环境交互。

传统的DL 方法选择最佳动作通常是基于查找表，而DRL 方法通过深度神经网络决策动作，大幅提升了解决复杂高维问题的能力。Mnih 等［24］通过DQN 解决以原始像素作为输入的高维复杂问题，这种方法在多个视频游戏中取得了与人类相当的表现。DQN 在处理离散动作空间的问题中游刃有余。然而，在涉及连续动作空间的机器人控制问题时，DQN 无法获得较好的结果。因此在应对连续动作的机器人控制问题就需要另外一种算法。

SAC 的核心理念是使用近似函数去学习连续动作空间的策略函数［25］。SAC 的目标是最大化智能体与环境交互中获得的奖励。为了实现这一目标，SAC 使用了软策略迭代。软策略迭代的过程在最大熵框架中交替进行，包括策略评估和策略改进两个步骤：策略评估是根据最大熵框架为当前策略找到精确的价值函数；策略改进是将策略分布更新为当前Q 函数的指数分布。SAC 使用神经网络作为近似函数，包括3 种神经网络：策略网络（用来表示策略函数）、价值网络（用来表示状态-价值函数）和软Q 网络（用来表示软Q 函数）。SAC 的策略网络训练通过最大化熵和奖励更新网络参数，这3 个网络的参数可以通过最小化误差进行优化。本文SAC伪代码如算法1 所示。

算法1 柔性演员-评论家（SAC）算法。

一般DRL 的目标是学习一个策略函数可以最大化有限范围时间T内的期望累积折扣奖励，即找到一个最大化的策略而本文的最大熵深度强化学习，除了上面的基本目标，还要求策略函数每次输出的动作熵最大：

其中H(π(⋅|s′))=-Ealogπ(a′|s′)。加入熵相后，就意味着神经网络需要探索所有可能的最优动作，而不是对于一种状态只考虑一个最优动作。因此双足机器人在面对干扰时可以更容易地作出调整。

令Qϕ(s，a)表示Q 值函数，πθ表示策略函数。这里考虑连续动作的设定，并假设πθ的输出为一个正态分布的期望和方差。Q 值函数可以通过最小化柔性Bellman 残差学习：

实际中，SAC 也使用了两个Q 值函数（同时还有两个目标Q 值函数）处理Q 值估计的偏差问题，即令Qϕ(s，a)=注意Jπ(θ)中的期望也依赖于策略πθ，可以使用似然比例梯度估计的方法优化Jπ(θ)。在连续动作空间的设定下，也可以用策略网络的重参数化优化。这样通常能减少梯度估计的方差。再参数化的做法将πθ表示成一个使用状态s和标准正态样本ϵ作为其输入的函数直接输出动作a：

将式（4）代入式（3）中得到：

其中：N 表示标准正态分布，现在πθ被表示为fθ。

最后，SAC 还提供了自动调节正则化参数方法。该方法通过最小化以下损失函数实现：

其中k是一个可以理解为目标熵的超参数。这种更新α的方法称为自动熵调节方法中。其背后的原理是在给定每一步平均熵至少为k的约束下，原来策略优化问题的对偶形式。

2.2 优化经验回放机制

与文献［26］中的经验回放机制不同，本文设计了一种经验分类单元和两个经验池。在经验分类单元中，使用余弦相似度方法对经验样本进行分类。首先，将训练产生经验样本存储在经验分类单元中；其次，在回合结束后利用余弦相似度方法计算经验状态与当前训练状态的相似度。相似度高的经验样本存储在高相似度经验池HE 中，相似度低的经验样本存储在低相似度经验池LE 中。给定两个状态s1和s2，对s1和s2的相似度计算规则如下：

状态相似度通过测量两个状态内积空间角度的余弦值表示：如果两个状态方向相同，则它们的状态相似度为1；如果两个状态方向垂直，则它们的状态相似度为0。每个经验样本根据相似度分类法存储于对应的经验池。

注意，高相似度经验池HE 的采样概率为μ，低相似度经验池LE 的采样概率为1 -μ，其中μ>0.5。

2.3 神经网络设计

在神经网络设计部分，主要分为3 个部分：神经网络结构、策略网络的输入和策略网络的输出。

2.3.1 神经网络结构

在SAC 的神经网络结构中，主要存在3 种神经网络：价值网络、软Q 网络和策略网络。所有层均以全连接层的形式连接。本文中用于测试的Atlas 双足机器人有30 个自由度，从中选取了影响Atlas 机器人行走的12 个重要参数作为策略网络输入的一部分；同时，还加入了质心的偏移作为影响双足机器人平衡的重要参数。策略网络的输出是Atlas 机器人腿部关节角度，包括12 个参数，也是策略网络的输入参数。而价值网络和软Q 网络的输入是机器人的状态参数，输出是单个参数。因此，策略网络的输入为15 个参数，输出为12 个参数，网络结构如图2 所示（CoM表示质心）。软Q 网络的输入还包括策略网络的输出。因此软Q 网络的输入为27 个参数，输出为1 个参数。价值网络的输入为15 个参数，输出为1 个参数。在隐藏层部分，策略网络、软Q 网络和价值网络使用的层数都是3。隐藏层的激活函数是ReLU（Rectified Linear Unit）。控制双足机器人腿部关节需要正值和负值，因此策略网络输出层的激活函数选择Tanh，Tanh 将输出值控制在[-1，1]。

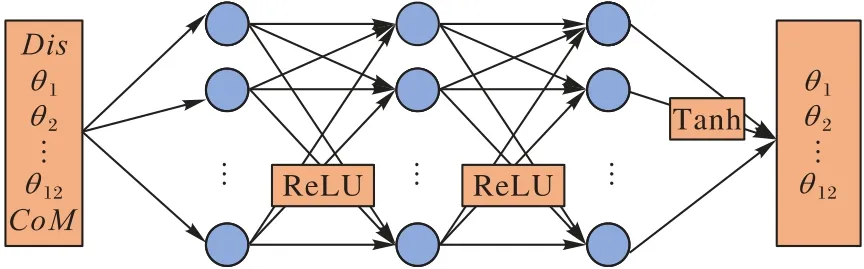
图2 策略网络结构Fig.2 Structure of policy network

2.3.2 策略网络的输入

策略网络的输入是双足机器人的状态空间。在构建状态空间时，许多现有的基于强化学习的双足运动方法使用机器人全部状态作为神经网络中策略网络的输入，显著降低了训练过程的采样效率，从而导致不必要的大型神经网络和延长训练时间；然而，状态空间还得考虑到变量的丰富性和必要性，因此，适当地选择一些有用的信息，让网络有良好的学习效率和结果很重要。本文的目标是让双足机器人快速、稳定地行走到100 m 外的终点，在行走过程中减少双腿自碰撞和摔倒。本文选取了影响双足机器人速度和稳定性的重要参数作为状态空间组成部分。状态空间如表1 所示。

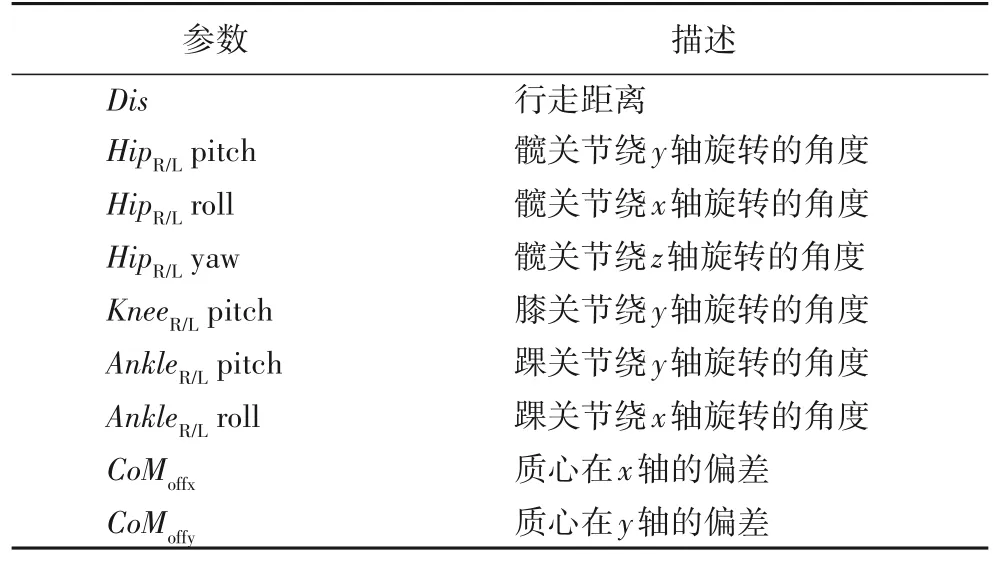
表1 状态空间Tab.1 State space

2.3.3 策略网络的输出

策略网络的输出是双足机器人的动作空间。动作空间是机器人与环境交互的方式。本文选取了影响Atlas 双足机器人行走的12 个重要参数作为Atlas 机器人的动作空间，Atlas 机器人采用不同的动作与环境交互，会获得不同的状态和奖励，因此策略网络的目标是输出使奖励最大化的动作。动作空间的参数如表2 所示。

表2 动作空间Tab.2 Action space

2.4 奖励函数

奖励函数对于DRL 算法至关重要，它直接指导整个算法的收敛方向，也是算法中任务目标的直接体现。因此，奖励函数的设计需要结合实际任务，明确最终目标。本文基于SAC 的步态控制方法的最终目标是控制双足机器人减少自碰撞，并在平坦的地面上完成连续稳定的直线行走。因此，双足机器人因自碰撞或其他问题而摔倒的次数可以作为奖励函数的一项。双足机器人在规定时间内连续稳定行走的距离也可以作为奖励函数的判断依据：双足机器人摔倒的次数越多，获得的惩罚越多；连续稳定行走的距离越远，获得的奖励越多。

理想情况下，当双足机器人能够连续稳定行走时，每一轮行走的距离应该相近。然而，在双足机器人训练的前期，由于无法获得连续稳定的步伐，在每一轮的训练中，取最大距离作为奖励函数的评定项。训练结束后，通过分析双足机器人摔倒次数和行走的距离判断双足机器人是否达到理想效果。还引入知识和经验设计多种奖励函数。该方法加速了DRL 算法的收敛，使双足机器人行走更快、更稳定。

2.4.1 速度和稳定性奖励

双足机器人的目标是稳定地直线行走到100 m 外的终点。如果在行走过程中摔倒或超过1 000 步，则本回合结束，获得一个值为-5+2.5 × (当前距离Dis/时间T)的惩罚奖励分数，并且重新开始下一回合的训练。如果双足机器人顺利完成100 m 距离的行走或者完成1 000 步，则会获得一个值为(距离Dis/时间T)的奖励分数，并且重新开始下一轮的训练 。在摔倒那一项奖励函数中加入 2.5 ×(当前距离Dis/时间T)，为的是鼓励双足机器人走得更远。而总体奖励函数中都除以时间T项，为的是提高双足机器人行走的速度。因此，速度奖励定义为：

为了保持双足机器人行走过程中的稳定性，本文考虑了双足机器人因双腿自碰撞，以及腿部零力矩点（Center of Mass，CoM）偏移过大而摔倒的问题。为了使双足机器人获得稳定的步态，必须对双足机器人设计稳定性奖励。

1）因双腿自碰撞而摔倒的问题。

双足机器人在行走时，髋关节容易带动腿在冠状面摆动，造成两条腿往相反方向运动，从而导致双腿发生碰撞而摔倒。稳定性奖励R2如下：

其中HipZsum=|AnglehipZL+AnglehipZR|。

2）因CoM 不在两腿坐标线中点而摔倒问题。

为了保持稳定性，本文采用游动腿的CoM 始终在两腿坐标线中点的标准进行训练。当CoM 不在中点时，该轮结束。稳定性奖励R3为：

其中Pshake=CoMoffx+CoMoffy。

2.4.2 约束奖励

强化学习训练时，可能会获得奇怪的行走姿势。为了使双足机器人行走更像人类，加入两个循环时钟，每个对应于机器人的一条腿：

其中：φt是一个相位变量，它从0 递增到1，然后回滚到0，跟踪步态的当前相位。恒定偏移0.0 和0.5 是相位偏移，用于确保左右腿在运动过程中的相位始终完全相反。

在双足机器人训练过程中，为了让双足机器人沿直线行走，必须控制双足机器人髋关节的摆动。约束奖励如下：

其中HipYsum=|AnglehipYL+AnglehipYR|。

综上所述，最终的奖励R定义为：

3 实验与结果分析

本文在Roboschool 平台使用SAC 步态控制方法对Atlas双足机器人进行训练，训练的内容是在平整路面上沿着某一固定方向直线行走。本文使用另外两种先进DRL 算法PPO和TRPO 进行对比实验。在同一环境、相同参数下，对Atlas双足机器人进行训练，下面给出仿真结果和对结果的分析。

3.1 学习速度和奖励值

本文用于训练的电脑配置如下：硬件环境为Intel Core i9-9900K 处理器，内存32 GB，显卡NVIDIA GTX 2080 Ti，软件环境为OpenAI Gym、Roboschool 和Chainerrl。训练过程中的奖励值如图3 所示（max 表示同一时间步下奖励的最大值，min 表示同一时间步下奖励的最小值）。从图3 中可以得出，本文SAC 算法相较于另外三种算法有很大提升，不仅是智能体奖励值的提升，而且还提高了收敛速度。

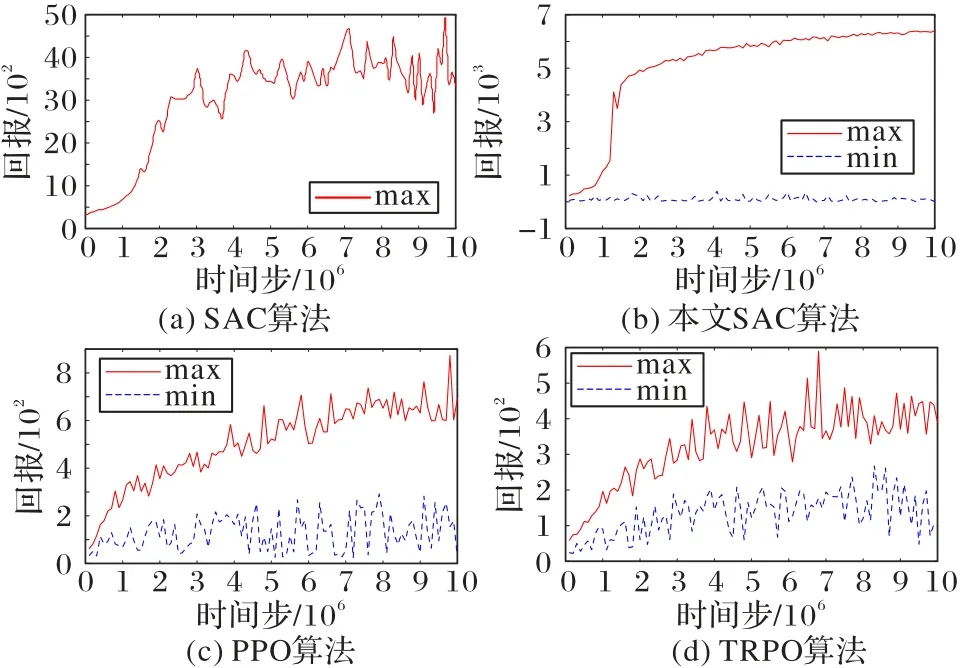
图3 四种算法的奖励值比较Fig.3 Comparison of reward values among four algorithms

在同一环境、相同的实验参数，本文测试了chainerrl［27］原本的SAC 算法和优化后的SAC 算法，以及另外两种先进的深度强化学习算法PPO 和TRPO。每一种算法，都在Roboschool 仿真环境里进行了1 000 万个时间步的训练。每10 万个时间步，对每个算法进行20 回合的评估。在这20 回合里取奖励值最大和最小回合的奖励值，并做了记录。最后绘制图3 所示的奖励值图。

在相同时间步的情况下，算法训练的智能体奖励值越大，学习速度则越高。而曲线的平滑性则与步态控制方法的鲁棒性密切相关，曲线越平滑，方法的鲁棒性越好。由图3可知，本文优化的SAC 与chainerrl 中原本的SAC 算法与其他两种先进的深度强化学习算法相比，本文算法收敛速度明显提高，并且实验的奖励值对比PPO 和TRPO 两种算法有很大的提升。优化的SAC 和SAC 算法在200 万时间步左右达到一个比较高的奖励值，而PPO 和TRPO 算法在600 万时间步左右才达到一个比较高的奖励值。从整体曲线的平滑性来看，本文优化的SAC 步态控制方法，有更快的收敛速度，以及更好的鲁棒性。

3.2 双足机器人步态控制结果与分析

由3.1 节可知本文SAC 步态控制方法具有良好的收敛速度和性能。3 种算法在同一台电脑上运行相同实验，PPO和TRPO 算法完成1 000 万个时间步需要30 h，而本文SAC 算法需要60 h。本文在训练Atlas 机器人直线行走时，并未实时渲染Atlas 机器人的训练情况。在3 种算法完成1 000 万个时间步后，本文使用3 种算法训练出来的最优模型参数控制Atlas 机器人直线行走。然而，只有本文SAC 算法具有成功控制Atlas 机器人实现直线行走的能力。其他两种算法对Atlas 机器人行走能力的控制的效果较差。

由图4 可知，本文SAC 算法实现Atlas 机器人直线行走能力最好，PPO 和TRPO 算法对Atlas 机器人行走控制还存在直线行走能力较差、行走磕绊、摔倒等问题。

图4 双足机器人在Roboschool中行走的细节Fig.4 Detail of biped robot walking in Roboschool

本文算法在Atlas 机器人步态控制中的仿真结果表明，Atlas 机器人可以完成1 000 步的行走，整个过程非常稳定，没有发生跌倒的情况；此外，Atlas 机器人实现了优异的直线行走能力。

踝关节控制双足机器人游动腿在落地时是否与地面平行。当与地面平行时，Atlas 机器人行走稳定。由图5 可知，Atlas 机器人在行走过程中，两条游动腿踝关节的角度相互交替，稳定地控制双足机器人在行走过程中启动和落地。后文图例中L/R 表示左/右，ak 表示踝关节，hip 表示髋关节，kn表示膝关节，x/y 表示x/y方向。

图5 踝关节角度的变化Fig.5 Changes in ankle joint angle

髋关节控制游动腿向前向后摆动，从而影响Atlas 机器人步长的大小。当Atlas 机器人游动腿的摆动角越大，说明Atlas 机器人的步长越大，则Atlas 机器人行走越快。由图6（a）所知，髋关节在Atlas 机器人前进方向上的摆动幅度足够大，说明Atlas 机器人行走快。此外，Atlas 机器人双腿前后摆动幅度相似，而且双腿有规律地前后摆动，这说明Atlas机器人行走也更类人。Atlas 机器人在行走过程中，不仅需要完成直线行走，还需要在行走过程中稳定不摔倒。由图6（b）（c）所知，髋关节还可以控制双腿在冠状面上摆动。而且左右腿的髋关节摆动有规律，控制Atlas 机器人的左右倾斜，从而影响Atlas 机器人行走的稳定性。本文提出的SAC 步态控制方法控制髋关节在影响Atlas 机器人直线行走和稳定性的方向上摆动幅度较小，而且左右腿的髋关节相互调节，控制Atlas 机器人直线行走的稳定性。最终，本文方法实现了Atlas 机器人稳定地直线行走。

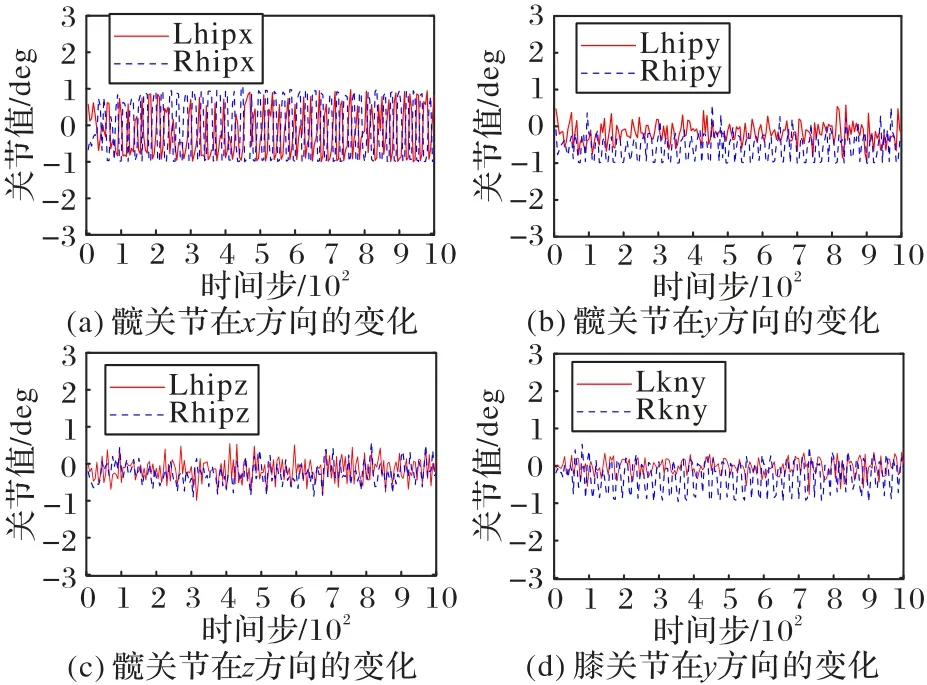
图6 髋关节和膝关节的角度变化Fig.6 Changes in angles of hip and knee joints

3.3 双足机器人干扰控制与鲁棒性分析

为了评估双足机器人直线行走的鲁棒性，本文参考文献［28］在两种不同的情况下向机器人躯干施加外力：1）向前方向施加外力；2）向双足机器人右侧施加外力。

值得注意的是，在整个双足机器人训练过程中没有向机器人躯干施加任何外力。在训练完成后，使用学习到的策略控制双足机器人在干扰情况下直线行走。

1）向前方向施加外力。

由图7 可知，在时间t=4 s，t=6 s 和t=8 s 时对Atlas 双足机器人躯干施加大小为15 N 的外力。图7（a）展示了在施加外力时，双足机器人速度对比之前的速度有小幅波动，但没有摔倒。在对双足机器人施加外力后，双足机器人速度的稳定性很快恢复。由图7（b）可知，在对双足机器人躯干施加外力时，双足机器人躯干向前倾斜角度增大。在下一时刻，双足机器人躯干恢复了一定的向前倾斜角度。

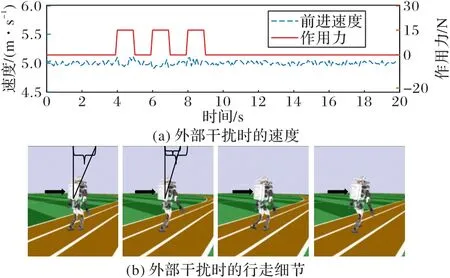
图7 向前施加外力时的鲁棒性控制Fig.7 Robust control when external forces being applied forward

2）向双足机器人右侧施加外力。

由图8（a）、（b）可知，在向双足机器人右侧施加外力时，双足机器人速度对比之前的速度有小幅波动，但是没有摔倒；尤其注意的是，双足机器人左右方向的移动速度。在向双足机器人右侧施加外力时，双足机器人控制髋关节抑制其向左边移动，可见双足机器人左右移动速度波幅渐大。在对双足机器人施加外力之后，双足机器人速度的稳定性很快恢复。在图8（c）中，本文在躯干中线添加一条指示线，当施加外力时，躯干向左扭转，指示线发生一定位移。在下一时刻，双足机器人很快恢复了躯干的扭转。

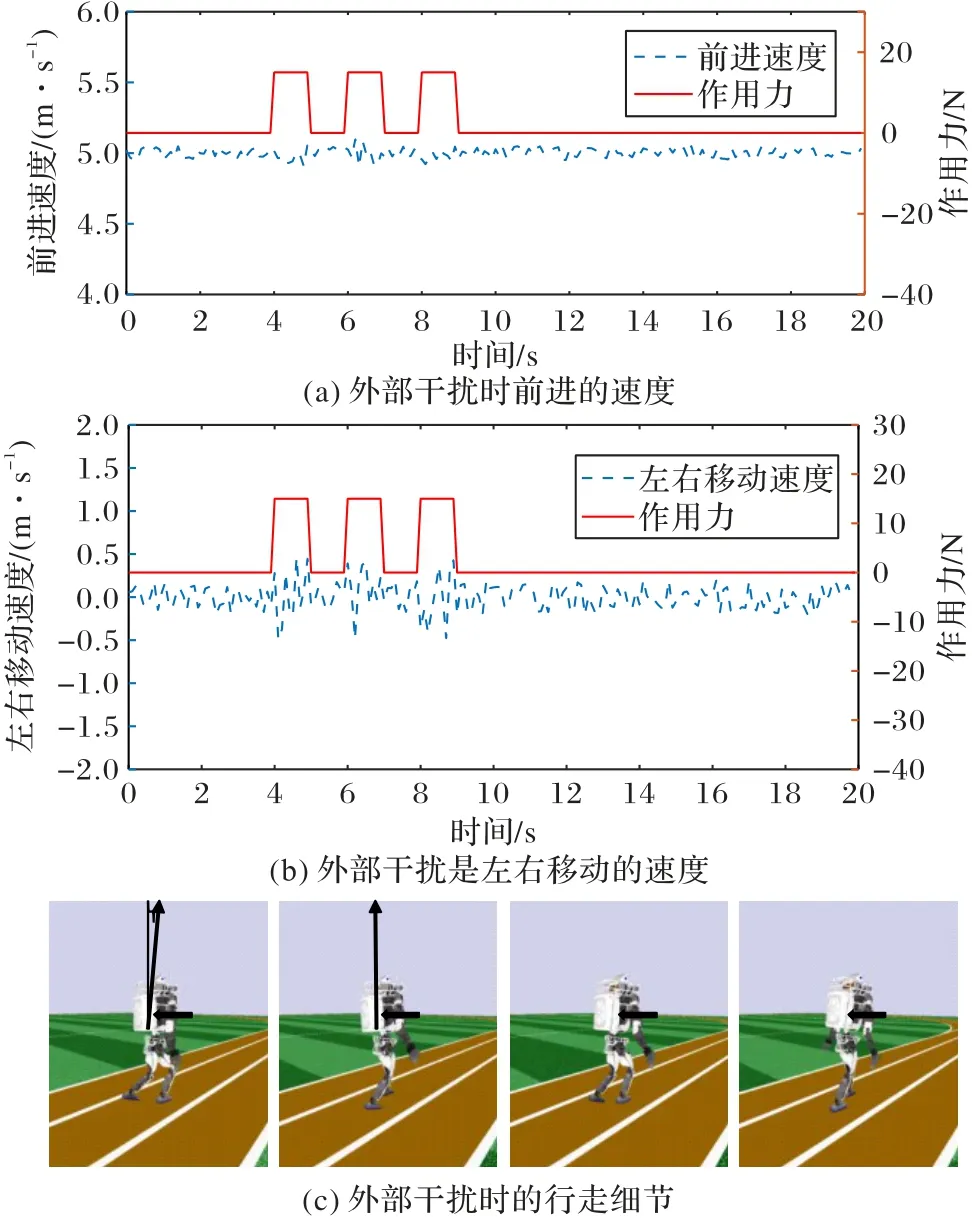
图8 向双足机器人右侧施加外力时的鲁棒性控制Fig.8 Robust control when external forces being applied to right side of biped robot

4 结语

本文针对双足机器人连续直线行走的步态稳定控制问题，提出一种基于深度强化学习SAC 的步态控制方法，该方法是基于最大熵的DRL 算法。它让策略尽可能随机，增大智能体的探索空间，避免策略过早地落入局部最优点，并且可以探索到多个可行方案完成指定任务，提高抗干扰能力。本文还采用了余弦相似度方法对经验样本进行分类，优化经验回放机制，提高样本效率。通过知识和经验来设计多种奖励函数，提高了双足机器人的训练速度和双足机器人快速稳定直线行走的能力。通过仿真实验表明，双足机器人完成了快速、稳定的直线行走，与其他深度强化学习算法相比具有较好的稳定性。未来工作将进一步优化步态控制方法，更好地控制双足机器人直线行走的稳定性，以及实现双足机器人在随机起伏地面的行走。