弯管内可控万向铰接柔性管动力学特性研究
林志强,罗 敏,王 晶,徐亭亭,李巧珍
(1.东北石油大学 机械科学与工程学院,黑龙江 大庆 163318; 2.东北石油大学 数学与统计学院,黑龙江 大庆 163318)
弯管内可控铰接柔性管常见于管道机器人[1-3]和超短半径水平井钻井[4]等行业,为了能够通过较大曲率的管道,柔性管被设计成多段铰接,行进过程中铰接柔性管存在由机构向结构转化的过程,柔性梁与外管的随机动态接触使得铰接柔性管的动力学行为尤为复杂,狭长空间内柔性管的动力学特性对柔性管自身的工作状态和安全性有着不可忽视的影响,研究弯管内可控铰接柔性管的动力学特性有着重要的工程意义。
铰接柔性管可以看成一个链式多体系统,针对链式多体系统,国内外学者开展了相关的力学分析。黄葆华等[5]结合Newton-Raphson迭代法和传递矩阵法,提出了求解大运动链式多体系统响应的可迭代增量传递矩阵法,该方法突破了传统传递矩阵法只能求解线性系统的限制,可用于非线性动力学系统的求解。赵强等[6]在链式多体系统结构动力学建模的研究中引入了空间算子代数和子结构分析法,该建模方法提高了精度与计算效率。徐妍等[7]基于柔性多体系统动力学理论,建立了多段铰接式扬矿硬管系统的拉格朗日动力学方程,通过相似理论实验验证了模型的合理性。谭小慧等[8]利用能量变分原理建立了含碰撞行为的非光滑链式多体系统动力学方程,对非光滑链式多体系统中的接触过程进行了数值模拟。张军等[9]将多跨铰接梁的每段单独研究,通过梁的振动力学方法,建立了其动力学模型,并进行了实验验证。罗敏等[10-11]采用有限元法,建立了管内可控万向铰接柔性杆接触非线性分析的数值计算方法,引入动力松弛法对数值模型进行求解,解决了梁-梁接触问题中由于刚体位移的产生导致非线性模型不收敛的问题,通过算例验证了模型的准确性。Kamman等[12]提出了一种基于“零特征值定理”的约束多体系统运动控制方程的建立方法,通过悬挂链的实例,验证了模型的合理性。Wang等[13]采用虚拟弹簧方法,对具有闭合运动链机械系统进行了动态仿真。该方法使用虚拟弹簧和阻尼器来包含运动学约束,从而避免了微分代数方程的求解,提高了求解效率。Omar[14]基于空间代数的多体动力学公式,提出了一种高效的链式结构的建模方法,采用弹性弹簧阻尼单元模拟链轮与链环之间的非线性三维接触力,并考虑了滑动摩擦,该方法可以用来预测链之间的接触力和磨损。Shafei等[15]提出了一种封闭环境下多刚性连杆动力学建模的系统方法,采用Gibbs-Appell递归方法推导运动控制方程,该方法建模效率较拉格朗日法高。Igor Mancilla[16]针对铰接式管道支撑位置受到振荡运动问题,考虑管道内的流体流动,利用Floquet理论,得到了铰接式刚性管道非线性运动方程的稳定性图,该方法计算成本比非线性数学模型的数值积分更低。
综上所述,在现有研究中,多是针对开放空间内的链式多体系统,而针对有限空间内具有动态接触行为的链式多体系统的动力学分析较少,且算法上多是将链式多体系统简化为刚体,算法的计算效率较高,但能考虑多体系统部件的应力和变形,虽然有学者研究了管内的铰接柔性杆的载荷传递规律,但在数值方法上采用大阻尼抑制振动,从而得到静力结果,方法上使求解收敛性得到了解决,但不能真实反映铰接柔性杆的动力学特性,且没有考虑钻头与岩石的互作用。因此,本文在前人基础上,考虑可控铰接柔性管底端的钻头与岩石互作用力模型,建立适用于弯管内可控铰接柔性管多体系统动态接触非线性分析的数值计算方法,开展弯管内可控铰接柔性管动力学特性研究,讨论不同施工参数对弯管内可控铰接柔性管动力学特性的影响规律,为可控铰接柔性管的结构设计和现场施工提供一定的理论参考。
1 弯管内可控铰接柔性管动态接触分析理论
弯管内铰接柔性管的结构示意图如图1所示。将柔性管和外管看做是三维有限应变管单元,柔性管之间通过可控铰连接,柔性管在外管内的径向运动受弯管内壁约束,采用管单元、可控铰接运动约束方程和管-管内接触模型描述弯管内可控铰接柔性管随机动态接触问题。
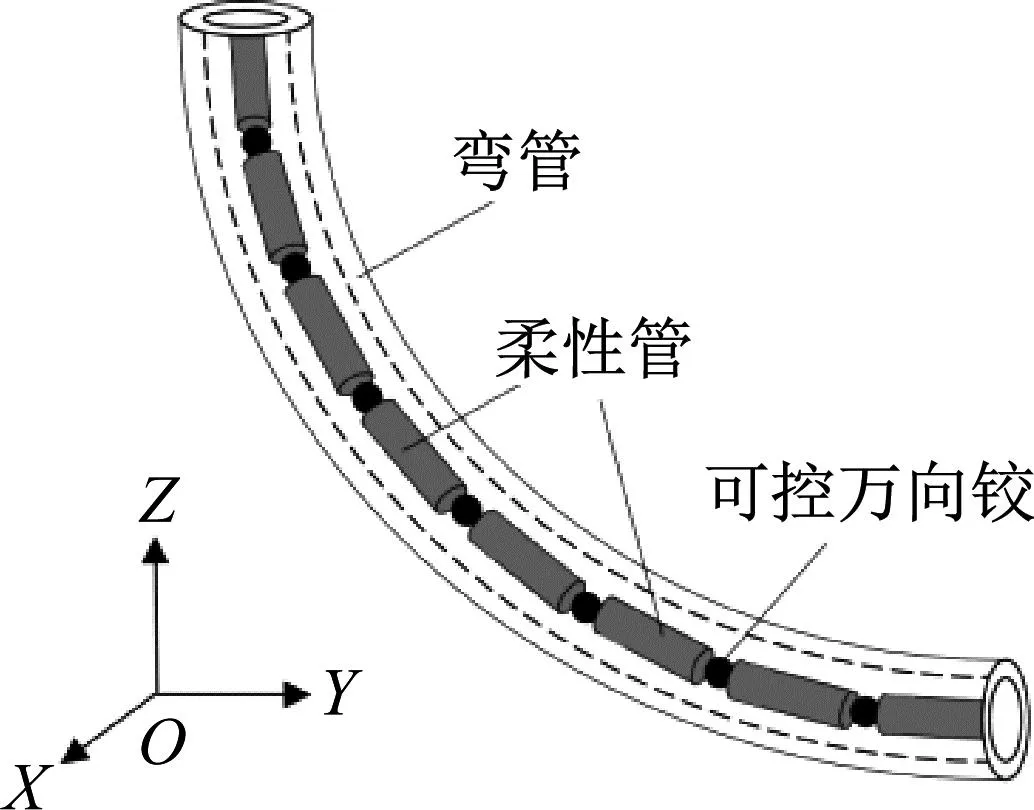
图1 弯管内可控万向铰接柔性管结构示意图
1.1 弯管内铰接柔性管多体系统接触非线性模型
1.1.1 可控万向铰接柔性管单元模型
(1) 空间管单元
将柔性管离散为空间管单元,单元长度为le,其节点位移示意图如图2所示。其中:x轴为管单元的中心轴;y、z轴为管单元截面主轴。
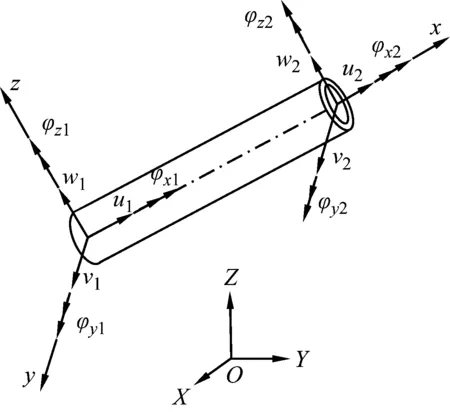
图2 空间管单元节点位移示意图
管单元内任意一点位移为
d=[u,v,w,φx,φy,φz]T=Nq
(1)
式中:u、v、w分别为管单元内任一点位移;φx、φy、φz为管单元节点转角;q为管单元节点位移列阵;N为管单元形函数矩阵[17]。
N=[Nu1,Nv1,Nw1,Nφx1,Nφy1,Nφz1,
Nu2,Nv2,Nw2,Nφx2,Nφy2,Nφz2]
(2)
q=[u1,v1,w1,φx1,φy1,φz1,
u2,v2,w2,φx2,φy2,φz2]T
(3)
根据变分原理
(4)
(5)
δd=Nδq
(6)
根据哈密顿原理推导管单元的动力学方程,哈密顿原理表达式为

(7)
式中:Up为管单元的应变能;Tp为管单元的动能;Wp为管单元的重力势能。
管单元的弹性应变能Up表示为
(8)
式中:ε为可控铰接柔性管的应变张量;σ为可控铰接柔性管的应力张量。
由于可控铰接柔性管x方向的维度要远大于其他方向,应变能表达式可以写为[18]
(9)
式中:εxx、εxy、εxz分别为柔性管x方向的正应变,xy平面、xz平面的切应变;E和G分别为柔性管的弹性模量和剪切模量;κ为剪切系数。
管单元的动能Tp为
(10)
式中:υ为柔性管的速度向量;ω为柔性管角速度向量;I为截面惯性矩矩阵;ρ为柔性管的密度;A为柔性管的截面积。
由于弯管的约束,可控铰接柔性管的φy和φz较小,可控铰接柔性管的速度向量υ、角速度向量ω和惯性矩阵I分别为[19]
(11)
式中:Ix为截面极惯性矩;Iy和Iz分别为绕y轴和z轴的转动惯量。
Ix=∬A(z2+y2)dA
(12)
(13)
(14)
式中:Do为柔性管外径;Di为柔性管内径。
管单元的重力势能Wp
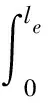
(15)
对管单元的弹性应变能Up、动能Tp和外力功Wp进行变分,得
(16)
(17)
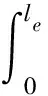
(18)
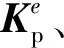
(19)
(20)
(21)
管单元的阻尼矩阵采用比例阻尼
(22)
式中,α和β为比例常数。
将单元矩阵进行组装,形成可控铰接柔性管的总体矩阵
柔性管的整体动力学方程写为
(23)
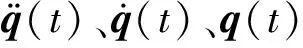
(2) 可控万向铰的运动约束
可控万向铰铰点矢量示意图如图3所示。在节点P、Q上建立可控万向铰的坐标系Pixiyizi和Qjxjyjzj,单元ei和单元ej通过P节点和Q节点的运动约束建立联系,定义固结在单元ei(节点P上)zi轴方向的单位矢量ai和单元ej(节点Q上)xj轴方向的aj2、yj轴方向的aj1以及连接铰点的矢量hij,可控铰的运动约束方程可以通过如图矢量间的运动关系定义。
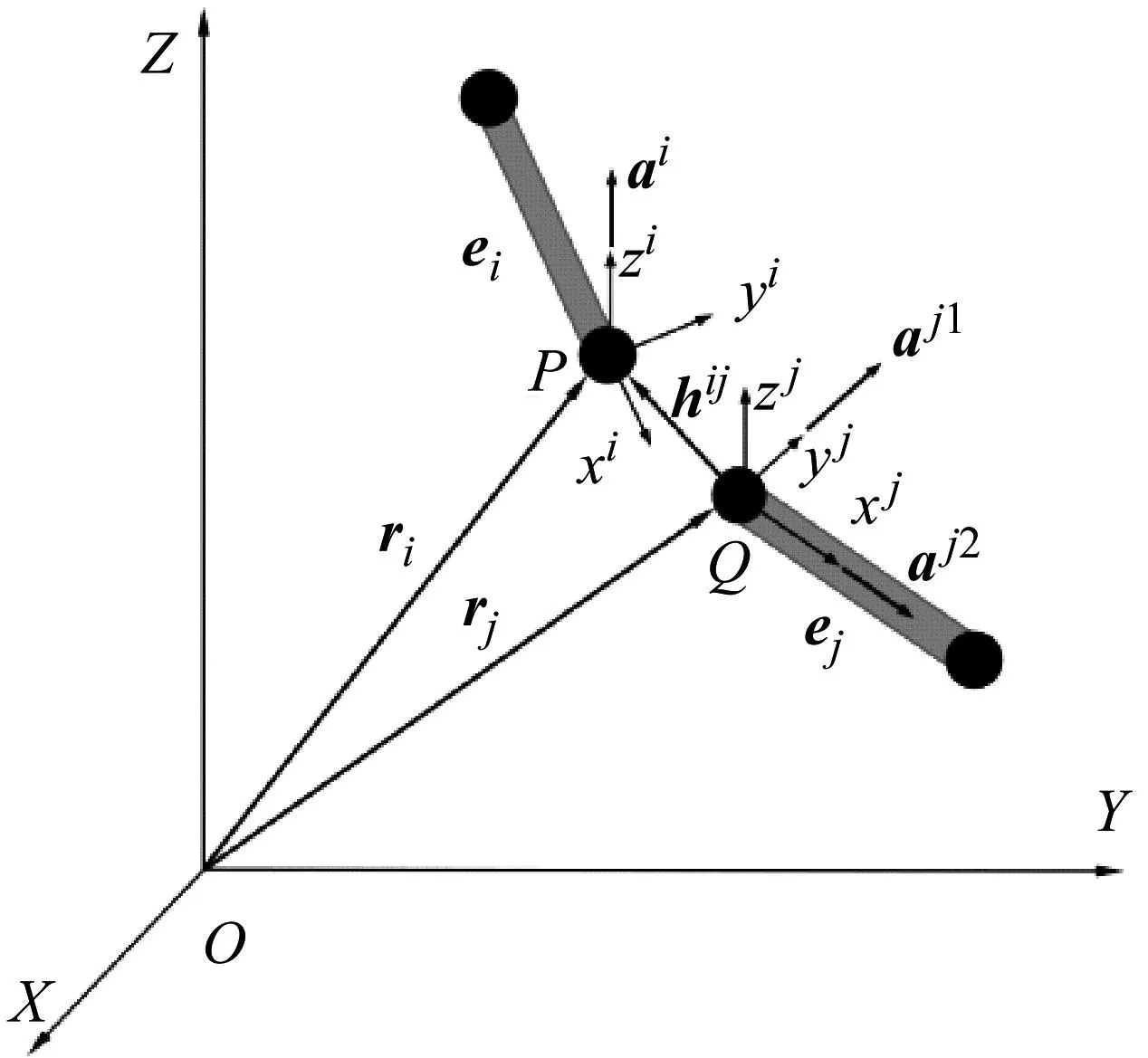
图3 可控万向铰铰点矢量示意图
P点和Q点在任意t时刻相对于整体坐标系原点O的矢径ri(t)和rj(t)为
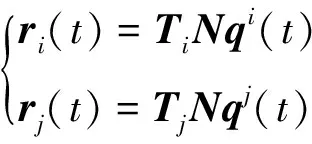
(24)
式中:Ti和Tj为单元坐标系的方向余弦阵[20];qi(t)和qj(t)分别为P和Q节点的位移向量;N为管单元的形函数矩阵。
两柔性管单元重合节点的相对平动约束可以通过限制矢量hij=QP的大小和方向确定
hij=ri(t)-rj(t)=0
(25)
可控铰的转动约束为
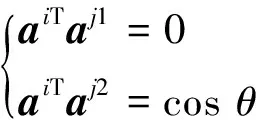
(26)
铰点处的约束方程为
(27)
设可控铰接柔性管整体由S个铰连接而成,则可控铰接柔性管的整体铰接约束方程为
(28)
采用拉格朗日乘子法[21]将约束方程引入到可控铰接柔性管的整体动力学方程中
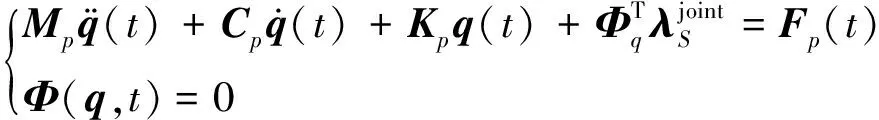
(29)
1.1.2 可控铰接柔性管与弯管接触分析模型
(1) 内管与外管接触判定条件
引入间隙函数g(t)定义内管与外管间的接触状态,通过内管节点Pm和外管节点Pn确定g(t),如图4所示。曲线上任意点的位置可以分别由局部坐标系em和en定义。
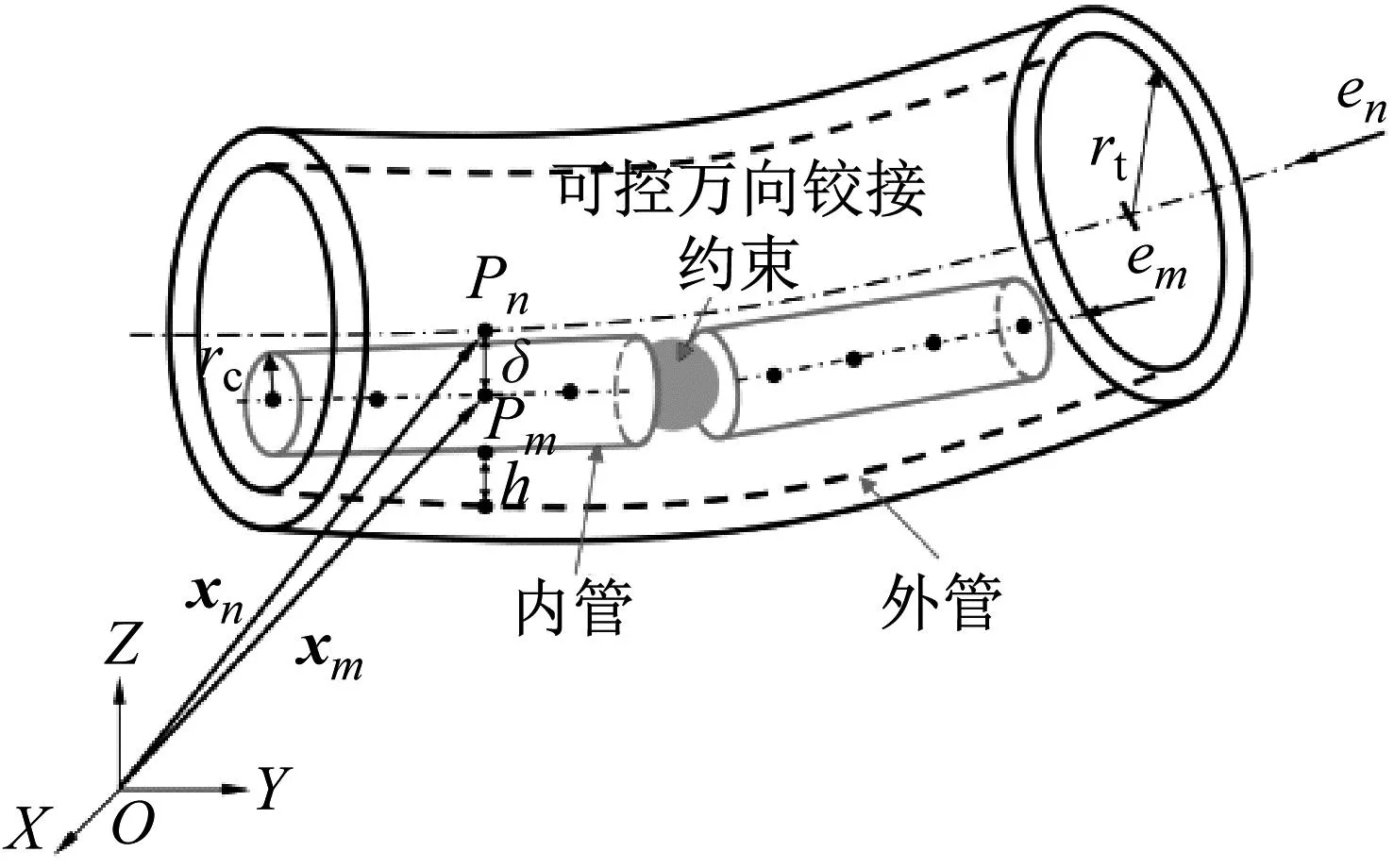
图4 可控万向铰接柔性管在管内接触模型
在整体坐标系OXYZ中,曲线上的每个点都与位置向量xm或xn相关联。由于间隙函数必须始终在当前构型中确定,在增量处理变形过程的每次迭代中,这些向量都对应于当前梁的构型。它们可以表示为初始构型点的位置向量Xm、Xn和位移向量um、un的和,即
xm=Xm+um
xn=Xn+un
(30)
通过节点Pm和节点Pn在全局坐标系中随时间变化的矢量位置,可以计算出它们之间的距离δ为
δ(t)=|xm-xn|
(31)
在计算出最接近点的距离基础上,间隙函数g(t)可由几何关系确定为
g(t)=rt-rc-δ(t)
(32)
式中:rt为外管的内半径;rc为内管的外半径。
当g(t)<0时,判定内管与外管发生接触,内管与外管发生接触后,采用增广拉格朗日算法计算法向接触力
(33)
其中
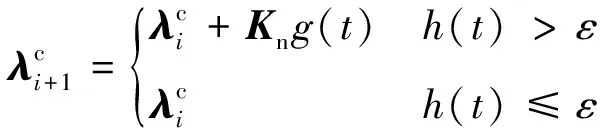
(34)
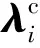
当内管与外管接触时,接触面有法向接触压力,若内管与外管发生相对滑动,有轴向摩擦阻力存在,本文采用库伦摩擦模型,表示如下
Ff=μFn
(35)
式中:Ff为摩擦力列阵;μ为摩擦因数。
综合可控铰接的机构-结构问题及与外管的接触非线性问题,结合管单元、可控铰接运动约束和管-管接触模型,建立弯管内可控铰接柔性管接触非线性的整体动力学方程为
(36)
由于方程存在非线性项,单独的动力学求解算法无法完成求解,采用Newmark法结合Newton-Raphson法[22]对弯管内可控万向铰接柔性管的整体动力学方程进行求解。
1.2 模型验证
采用文献[23]中的算例,对本文数值计算方法进行验证。内管弹性模量E=210 GPa,l=1 m,惯性矩I=7.84×10-9m4,内管与外管间隙δ=8 mm,铰点处的铰接限制度数χ=1°。外管全固定,内管一端固定约束,一端为可动铰支约束,中间铰接处受集中载荷作用F(t)=1 000t(0≤t≤0.08)(单位N)如图5所示。
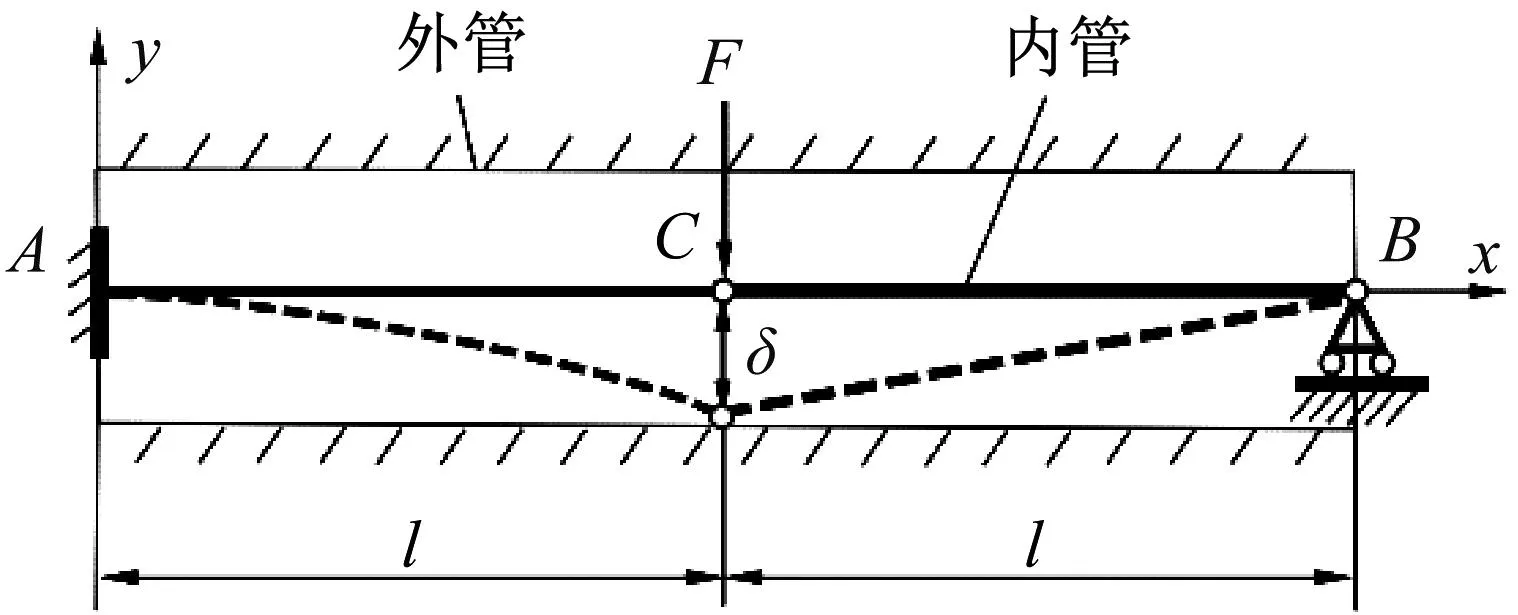
图5 内管与外管结构示意图
铰点处的y方向位移Δ的解析解为
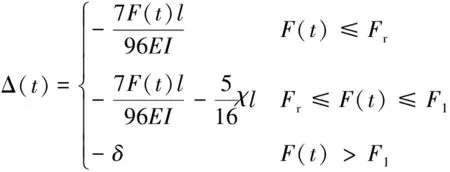
(37)
式中:Fr为铰接处达到转动限制度数的临界集中力;F1为内梁与外梁发生接触的临界集中力,本算例中Fr=34.48 N,F1=57.49 N。解析解与数值解对比如图6所示。由图6可知,最大误差仅为0.9%,计算模型满足精度条件。
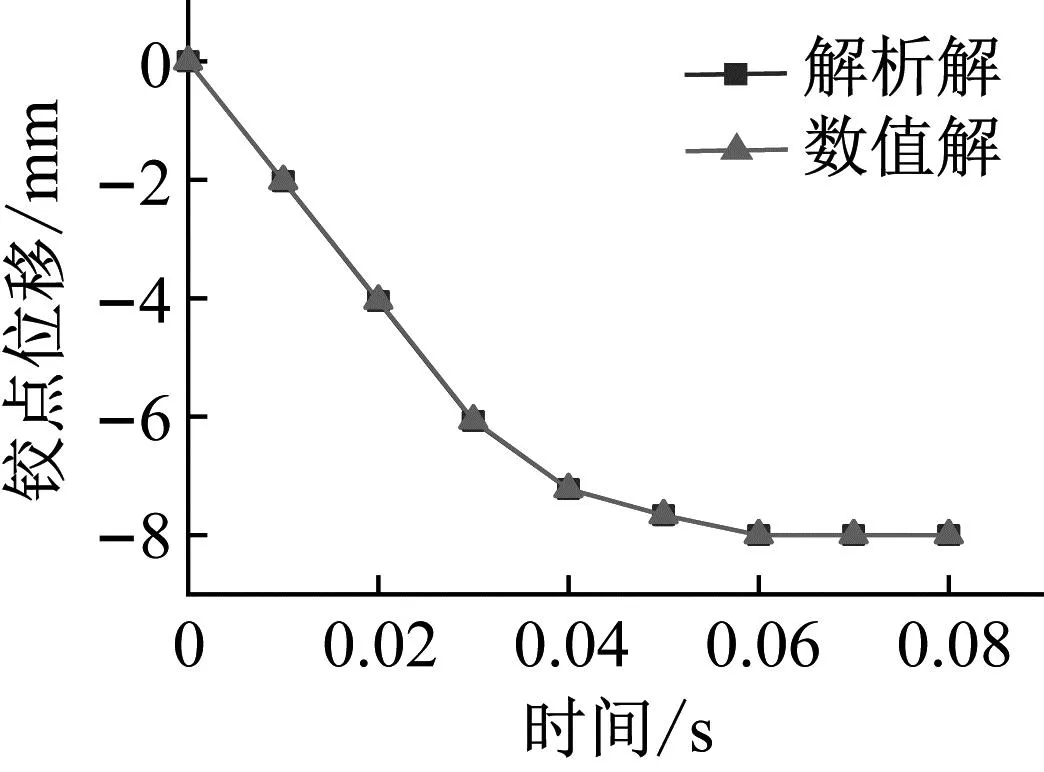
图6 铰点位移解析解与数值解对比
2 工程算例
将弯管内可控铰接柔性管多体系统非线性动力学模型应用到钻井工程中,采用文献[24]中的施工参数,对超短半径水平井造斜段柔性钻具进行动力学分析。
2.1 柔性钻具动力学分析模型的建立
超短半径水平井造斜段曲率半径ρ为3.2 m,井斜角为90°,选取柔性钻杆和导向筛管为研究对象,导向筛管和柔性钻杆的弹性模量E=210 GPa,泊松比为0.3,密度为7 850 kg/m3。将柔性钻杆简化为相应截面尺寸的圆管结构,简化后的结构如图7所示。单节柔性钻杆各截面S1~S5对应的长度分别为33 mm、28 mm、38 mm、32 mm和27 mm,对应的外径分别为54 mm、84 mm、84 mm、91 mm和69 mm,内径均为30 mm,铰接位置位于截面S2和截面S3之间。
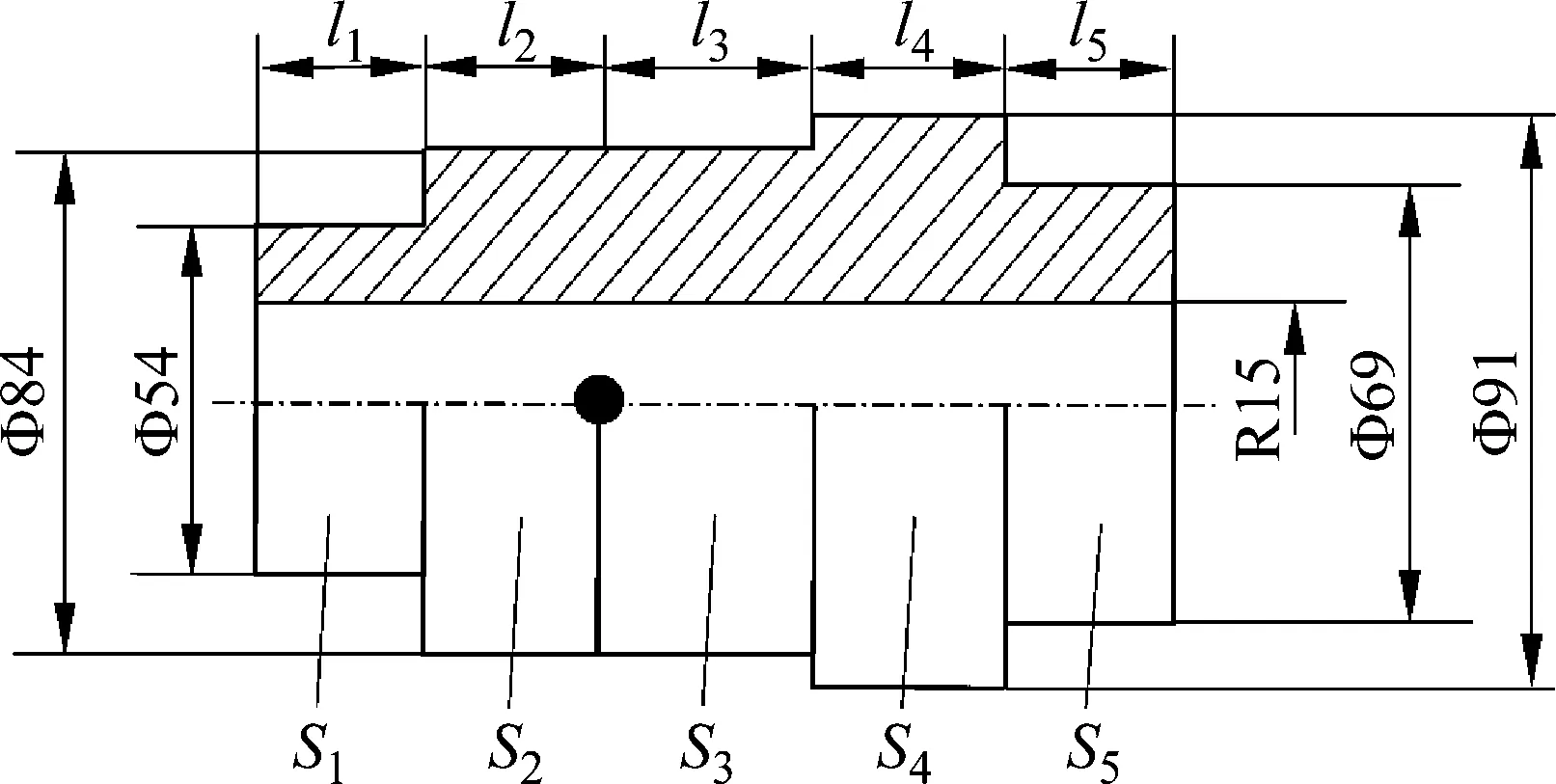
图7 简化后单节柔性钻杆结构
柔性钻具动力学分析模型如图8所示,柔性钻杆的截面由x轴(方向垂直平面向里)和y轴(与x轴垂直,方向指向井眼曲率半径圆心)描述,z轴为柔性钻杆的轴向。
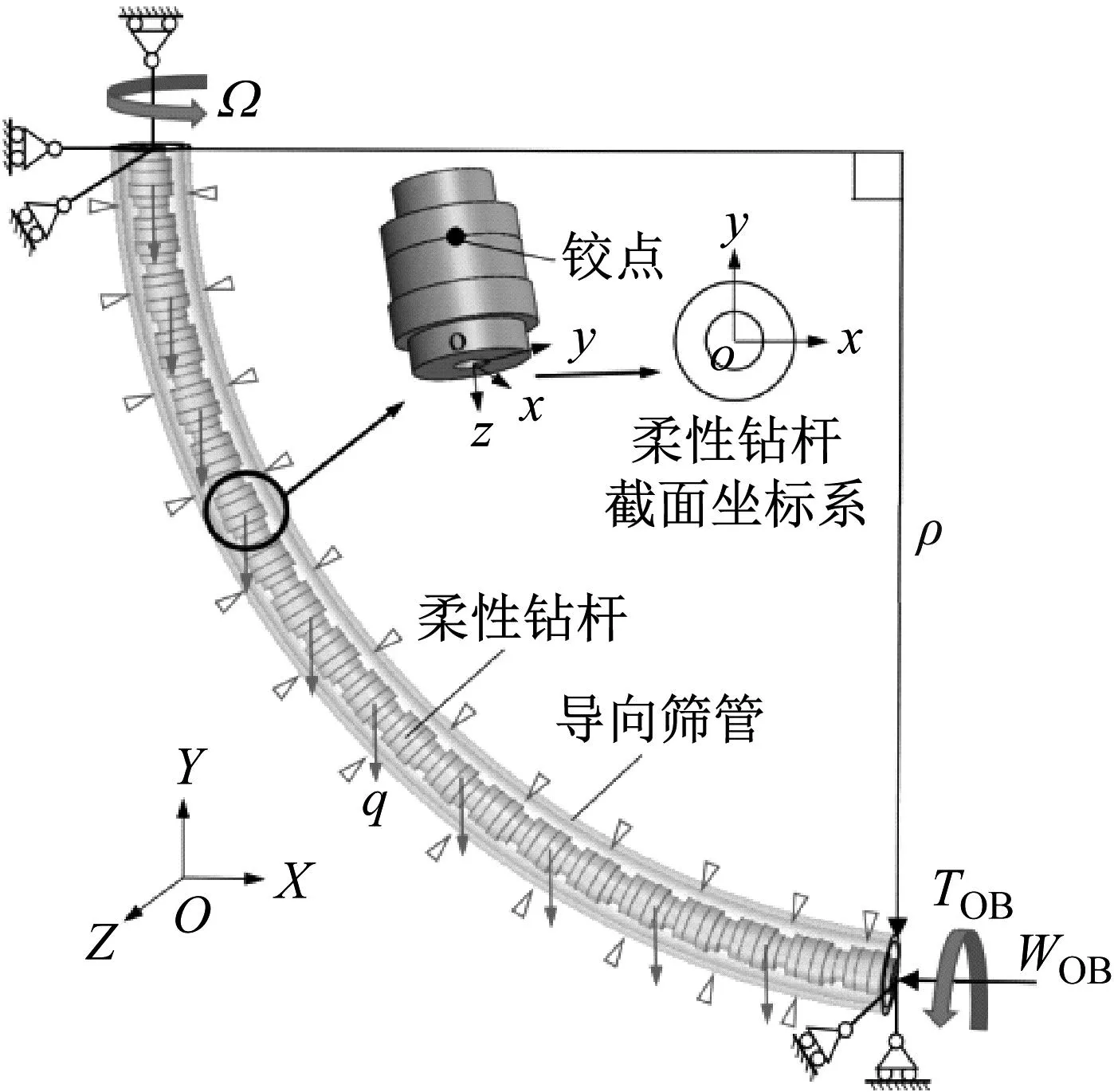
图8 柔性钻具动力学分析模型
柔性钻具的边界条件为:导向筛管全固定约束,柔性钻杆顶端施加三个方向的线位移约束,底端施加x方向与y方向的线位移约束,柔性钻杆顶端施加转速(r/min),转速施加表达式如下
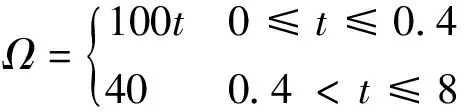
(38)
柔性钻杆底端施加钻头与岩石互作用简化模型[25]。计算公式如式(39)所示,计算过程中钻头与岩石动摩擦因数取0.235,钻压为3 t。
(39)
式中:TOB为钻头由于摩擦产生的总扭矩;η为钻头与岩石间的动摩擦因数;D为钻头直径;WOB为钻头上钻压。
柔性钻杆同时承受自重作用,重力加速度取9.8 m/s2,数值模拟计算总时长8 s,其中0~0.4 s为转速加载阶段,0.4~8 s为正常钻进阶段,计算时间步长为0.04 s。
2.2 柔性钻杆振动特性分析
柔性钻杆的振动可以分为横向振动、轴向振动、扭转振动和涡动四种。美国贝克休斯公司将钻柱的振动分为三项水平,即横向振动水平、轴向振动水平和黏滑振动水平,每个振动水平分为0~7级[26],其中,轴向振动水平在4级及以上为剧烈振动,横向振动水平和黏滑振动水平在5级及以上为剧烈振动,钻柱易产生破坏。
(1) 柔性钻杆的横向振动
柔性钻杆横向加速度有效值(计算时长内加速度的均方根值)[27]随井斜角位置变化曲线如图9所示。由图9可知,由于铰接位置存在结构与机构间的转换,导致了柔性钻杆的横向振动具有不连续的特点,且振动峰值均出现在铰点位置,x方向的横向振动和y方向的横向振动具有极高的相似性,x方向的横向振动明显大于y方向的横向振动,且靠近两端位置的振动更大,x方向和y方向横向振动最大值分别为15.25g和7.70g(g为重力加速度),柔性钻杆x方向横向振动剧烈位置集中在井斜角38°~86°,y方向横向振动剧烈位置集中在井斜角49°~59°,x方向横向加速度值处于剧烈振动区间占比56.28%,y方向为19.89%。由此可知铰接位置的x方向横向振动更容易使柔性钻杆发生失效。
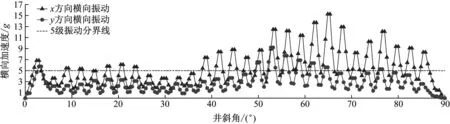
图9 柔性钻杆横向加速度随井斜角位置变化曲线
(2) 柔性钻杆的轴向振动
柔性钻杆的轴向振动加速度有效值曲线如图10所示。由图10可知,柔性钻杆的轴向振动较小,最大值为2.34g,出现在井斜角4.39°位置,达到3级振动水平,其余位置的振动均处在2级振动以下,较为安全。
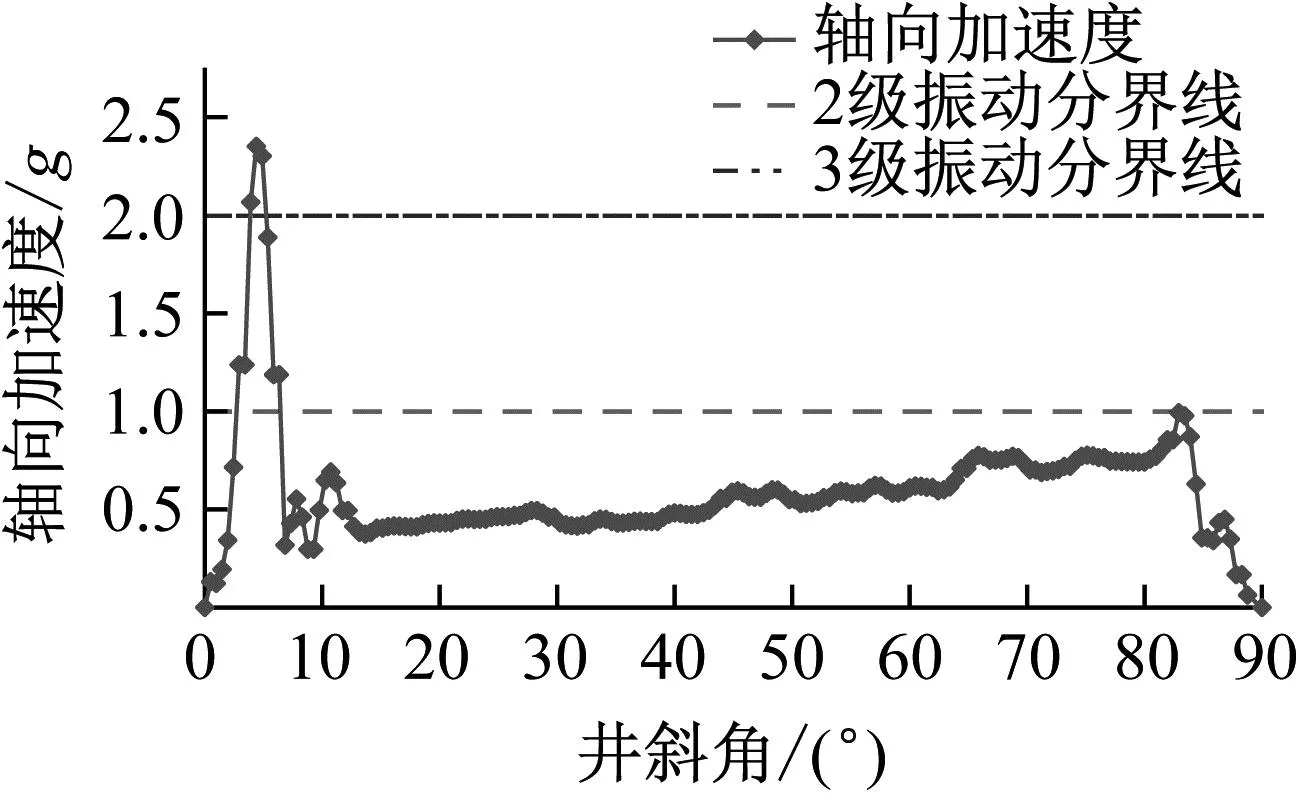
图10 柔性钻杆轴向加速度随井斜角位置变化曲线
(3) 柔性钻杆的黏滑振动
黏滑振动由S1和S2两个指标描述,计算式为
(40)
(41)
式中:Nmax、Nmin和Na为柔性钻杆底端最高、最低转速和平均转速,r/s;tbak为柔性钻杆反向涡动所占时间;ttotal为总计算时长。
柔细钻杆顶端与底端转速对比如图11所示。
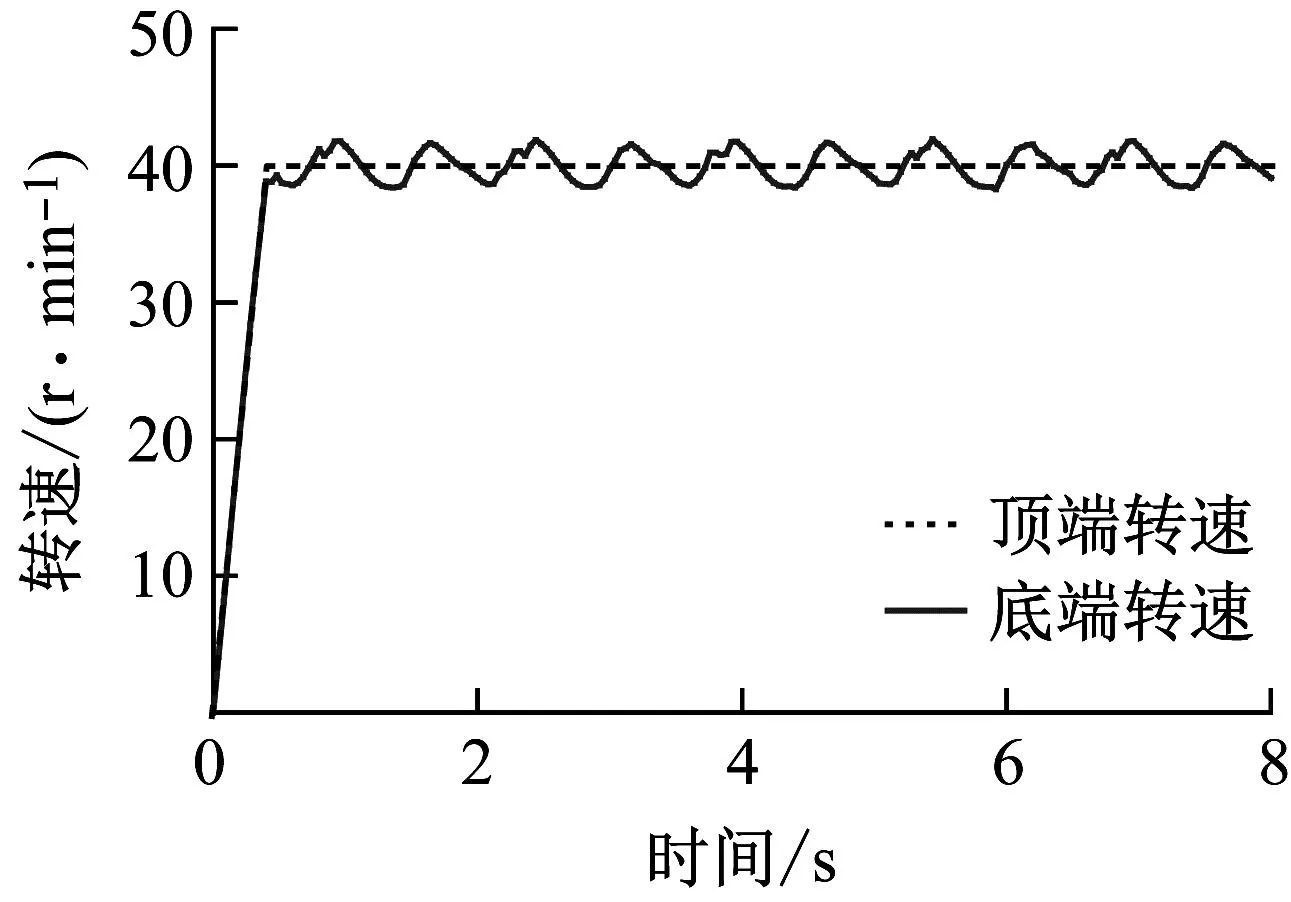
图11 柔性钻杆转速随时间变化曲线
由图11可知,正常钻进阶段底端转速呈现正弦趋势,底端最高转速和最低转速分别为41.93 r/min和38.28 r/min,顶端转速稳定后底端的平均转速为39.98 r/min,为了便于代入式(40)和式(41),将上述转速的单位转换为r/s,分别为0.70 r/s、0.64 r/s和0.65 r/s。
不同位置柔性钻杆运动轨迹如图12所示。由图12可知,柔性钻杆两端的涡动范围较大,中间涡动范围相对较小,三个位置绕中点的公转方向均为逆时针(与顶端转速施加方向相同),结合柔性钻杆的转速对比得出,柔性钻杆没有出现反向涡动现象。通过计算得到,S1=0.25,S2=0,柔性钻杆的黏滑振动处于1级水平。
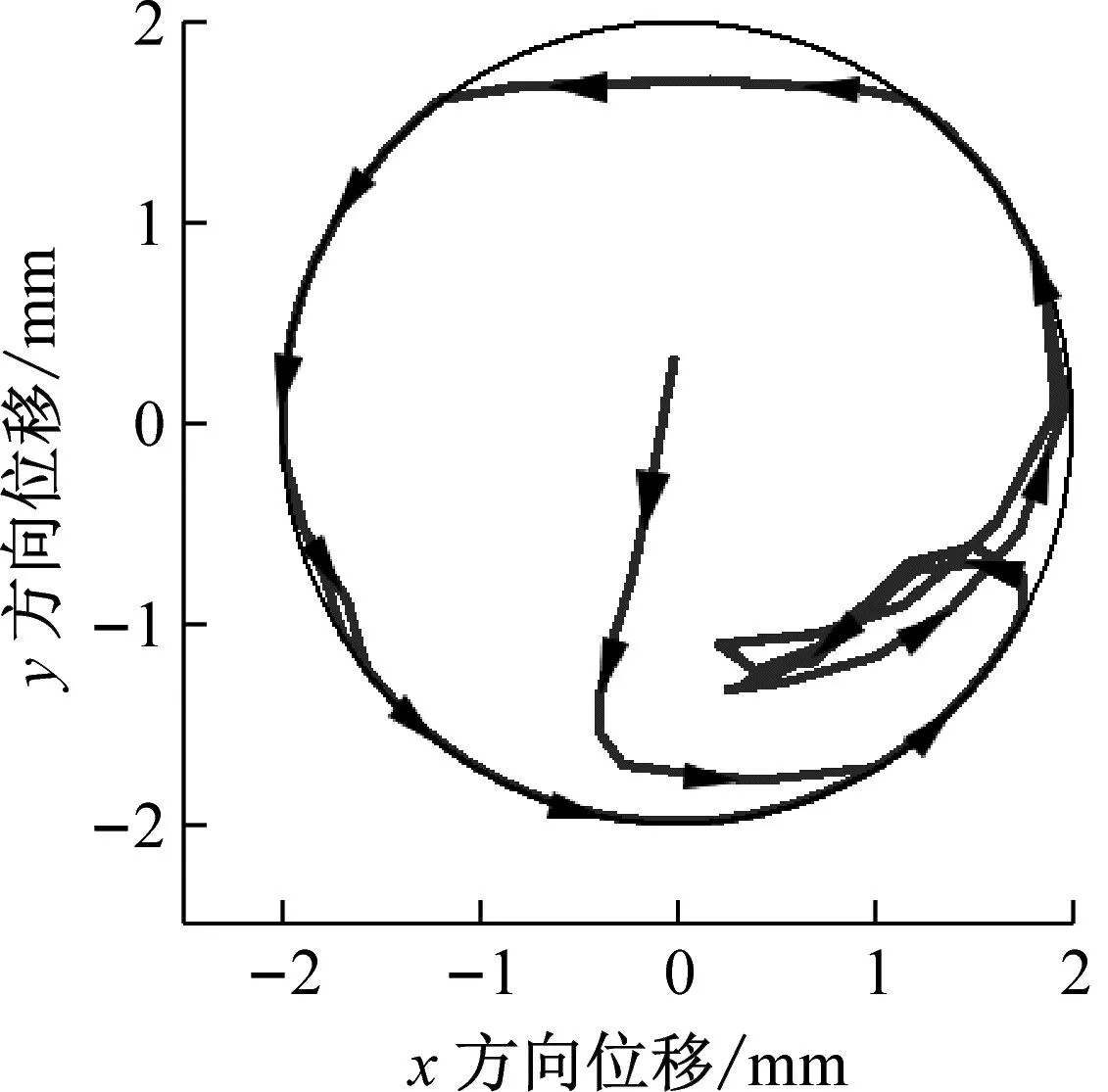
(a) 顶端
2.3 柔性钻杆振动特性影响因素
由2.2节可知,造斜段柔性钻杆的失效最有可能由横向振动引起,而柔性钻杆x方向和y方向的横向振动具有相似性的特点,x方向的横向振动又明显大于y方向的横向振动,因此,本节主要研究转速和钻压对柔性钻杆x方向横向振动的影响。
(1) 转速对柔性钻杆横向振动的影响
固定钻压为3 t,令转速分别为40 r/min、50 r/min和60 r/min,不同转速下柔性钻杆横向振动加速度随井斜角位置变化曲线如图13所示。由图13可知,在转速为40 r/min、50 r/min和60 r/min时,柔性钻杆x方向横向振动的最大值分别为15.25g、12.90g和13.82g,产生剧烈振动位置占比分别为56.28%,46.44%和39.89%。从图中可以看出,在井斜角0°~10°区间内,柔性钻杆的横向振动随着转速的增加而增大,在区间10°~46°和区间78°~90°,转速对横向振动剧烈程度的影响不大,在区间46°~72°,柔性钻杆的横向振动随着转速的增加而减小,总体上看,增加转速在一定程度上减小了柔性钻杆的整体横向振动剧烈程度。
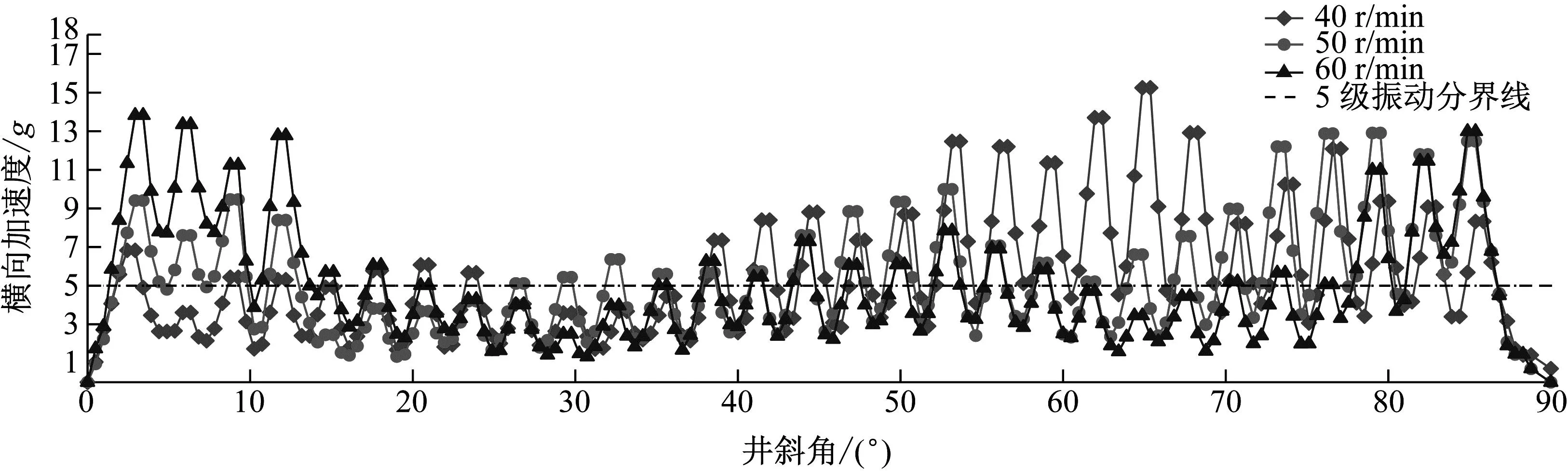
图13 不同转速下柔性钻杆x方向横向加速度随井斜角位置变化曲线
(2) 钻压对柔性钻杆横向振动的影响
固定转速为40 r/min,令钻压分别为3 t、6 t和9 t,不同钻压下柔性钻杆横向振动加速度随井斜角位置变化曲线如图14所示。由图14可知,在钻压为3 t、6 t和9 t时,柔性钻杆x方向横向振动的最大值分别为15.25g、27.22g和23.55g,三种钻压下,柔性钻杆产生剧烈振动位置占比分别56.28%,70.49%和90.00%。从图14可以看出,钻压增大到6 t时,对井斜角10°~20°区间内的柔性钻杆横向振动影响不大,由井斜角23°开始柔性钻杆的横向振动急剧增加,直到井斜角43°位置达到最大值。钻压为9 t时,井斜角3°~15°、17°~86°区间内,柔性钻杆的横向振动均达到剧烈振动水平,柔性钻杆整体基本进入危险状态。由此可见,增大钻压,柔性钻杆横向振动急剧增大,不利于安全钻进。
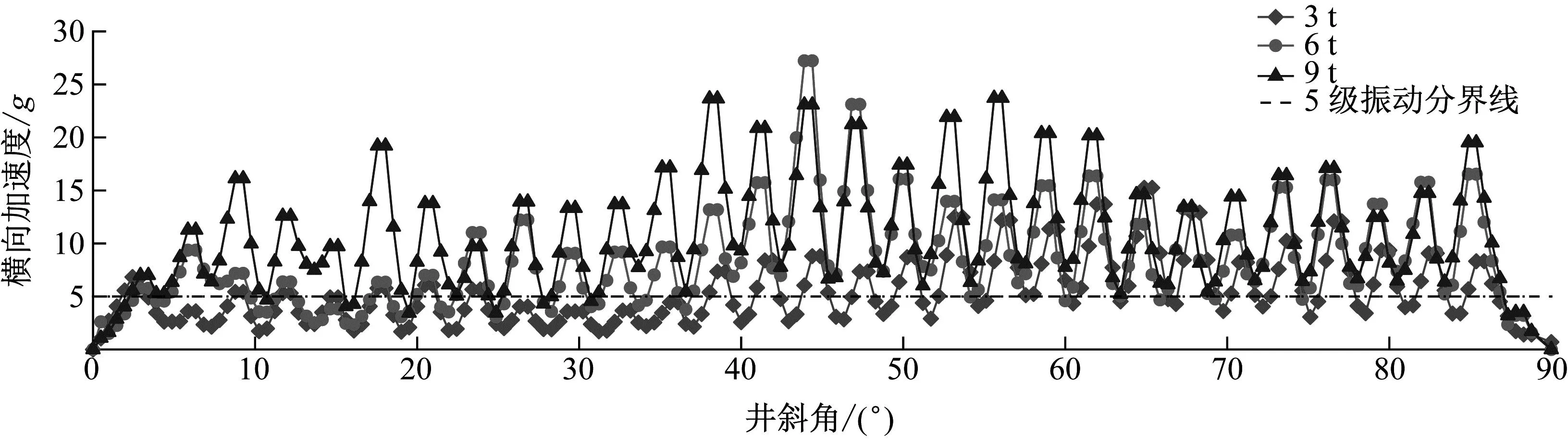
图14 不同钻压下柔性钻杆x方向横向加速度随井斜角位置变化曲线
3 结 论
本文采用哈密顿原理结合多体系统动力学理论,建立了弯管内可控铰接柔性管多体系统动态接触非线性力学模型,通过算例验证了模型的准确性。以超短半径水平井柔性钻具为例,对造斜段柔性钻具进行动力学分析,得到以下结论:
(1) 在超短半径水平井造斜钻进过程中,柔性钻杆的轴向振动和黏滑振动处于安全水平,横向振动是导致柔性钻具可能失效的主要因素。
(2) 增大转速可以在一定程度上减小柔性钻杆的横向振动;增大钻压,不利于柔性钻杆的安全钻进。

