非晶态碳薄膜对金属二次电子发射的影响*

胡笑钏 刘样溪 楚坤 段潮锋

1) (长安大学能源与电气工程学院,西安 710064)

2) (西安交通大学医学部,西安 710049)

非晶态碳薄膜由于具有极低的二次电子发射系数(secondary electron yield,SEY),在真空微波器件与设备异常放电领域引起了广泛关注.然而,非晶态碳薄膜对二次电子发射影响的动态过程及微观机理仍缺乏了解.本文采用Monte Carlo 方法,建立了Cu 表面非晶态碳薄膜的二次电子发射数值模拟模型,能够精确地模拟电子与薄膜及基底材料的散射及二次电子发射的微观物理过程.结果表明,随着薄膜厚度从0 nm 增加至1.5 nm时,SEY 峰值下降了大约20%;继续增大厚度,SEY 峰值不再下降.然而,当薄膜厚度大于0.9 nm时,SEY 曲线呈现出双峰形态,但随着薄膜厚度增加至3 nm,第二峰逐渐减弱甚至消失.电子散射轨迹和二次电子能量分布结果,表明这种双峰现象是由于电子在两种材料中散射所致.相比以往模型,所提模型考虑了功函数的变化以及界面势垒对电子散射路径的影响.该模型从微观层面上解释了SEY 曲线双峰现象形成的原因,相关的计算结果为非晶态碳薄膜对SEY 的抑制规律提供了理论预测.

1 引言

二次电子发射现象是引起高能粒子加速器、真空微波元器件和其他电子设备异常放电的重要因素[1–3],受到相关领域研究人员的广泛关注.例如,在高能粒子加速器的真空室中,由残留气体电离产生的电子束与真空腔壁碰撞产生二次电子,从而形成电子云,并导致束流损失或真空恶化[4,5].二次电子发射系数(secondary electron yield,SEY)定义为二次电子数目与入射电子数目之比,是表征二次电子发射现象的重要特征参数.因此,抑制二次电子发射现象或降低金属表面SEY 是提高真空微波部件和设备放电阈值的重要途径.

二次电子一般从材料表面纳米深度中出射,对表面状态非常敏感[6,7],因此通过表面镀膜能够有效抑制二次电子发射[8,9].近年来,非晶态碳(amorphous carbon,a-C)薄膜被发现在抑制二次电子发射方面具有巨大潜力[10,11].Larciprete 等[12]在Cu基底上制备纳米厚的a-C 薄膜,使Cu 的SEY 峰值从1.4 降低到1.2.Li 等[13]在实验中发现a-C 薄膜不但能够使不锈钢基片的SEY 降低30.6%,同时可以增大第一和第二临界能量,从而降低微波器件异常放电风险.除此之外,a-C 薄膜还具有成本低、化学性质稳定、易制备等特点,促进了该材料在抑制二次电子发射领域方面的应用.然而,有学者在实验中观察到了这种薄膜结构的SEY 曲线在某些特定情况下呈现出了双峰形态,这一现象很可能引起微波管内额外损耗,从而影响器件性能、工作寿命和传输质量[14,15].

有关a-C 薄膜对二次电子发射的影响规律大多仍停留在实验阶段,相关的理论研究仍然匮乏.并且,实验中观察到的双峰现象及其形成原因尚未得到充分的理论解释.Monte Carlo (MC)方法在粒子碰撞动力学模拟方面具有天然的优势,通过MC 模拟可以获得材料内部的电子散射过程以及二次电子发射特性的详细信息,非常适合从微观层面解释二次电子发射特性的形成规律[16–18].Nguyen 等[19]采用MC 方法模拟了石墨烯薄膜的二次电子发射过程,其中电子的弹性散射和非弹性散射分别采用经典的Rutherford 弹性散射截面[20]和Bethe 能量损失公式[21]描述.

本文在已有电子与金属基底散射模型基础上,采用MC 方法建立了Cu 表面a-C 薄膜的二次电子发射数值计算模型,模拟了电子在a-C 薄膜和Cu 基底内的散射过程及二次电子发射过程,其中弹性散射和非弹性散射分别采用Mott 微分散射截面法和Penn 介电函数方法描述.通过记录电子散射轨迹和统计二次电子信息,探讨a-C 薄膜对Cu 的二次电子发射效应的抑制规律和双峰现象形成的原因.

2 研究方法

根据a-C 的厚度和入射电子能量,电子在a-C/Cu 内的散射可以分三种情况讨论,如图1 所示.情况1: 如果a-C 极薄,电子可以直接穿透a-C 并与Cu 基底散射,因此a-C 几乎不会影响散射过程;情况2: 如果a-C 较厚且入射电子能量较低,电子只能在a-C 内散射,无法到达Cu 基底;但如果入射电子能量较高,电子会同时在a-C 和Cu 中散射(情况3).电子无论在a-C 或Cu 中均可能发生电离散射事件,并产生新电子,这些新电子与入射电子同时被追踪,直到电子出射到真空中或其能量耗尽在材料中.此外,a-C 薄膜还会通过影响金属表面功函数而改变电子出射概率,因此真空/ a-C 界面和a-C/Cu 界面对电子散射和出射的影响需要在模型中予以考虑.

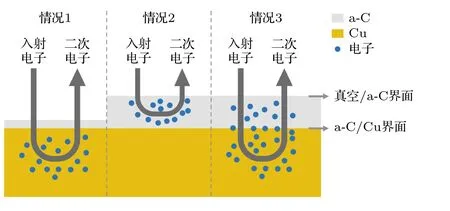
图1 a-C/Cu 的二次电子发射示意图Fig.1.Schematic diagram of the secondary electron emission of a-C/Cu.

基于MC 方法的a-C/Cu 二次电子发射数值模拟流程如图2 所示.首先,根据电子的位置判断发生散射的材料种类.若在Cu中,电子与Cu 原子的散射过程通过之前报道的模型进行模拟[22].若在a-C中,首先根据散射截面确定电子与C 原子的散射类型.若为弹性散射,只改变电子运动方向,若为非弹性散射,还需更新电子能量,并确定是否生成新的电子,这些新电子也同样被追踪.然后,根据电子下一次的散射位置判断其是否从表面出射.若出射,则记录其信息,包括出射能量、出射角度、出射点位置和电子散射轨迹;否则,电子将在材料内继续执行散射.

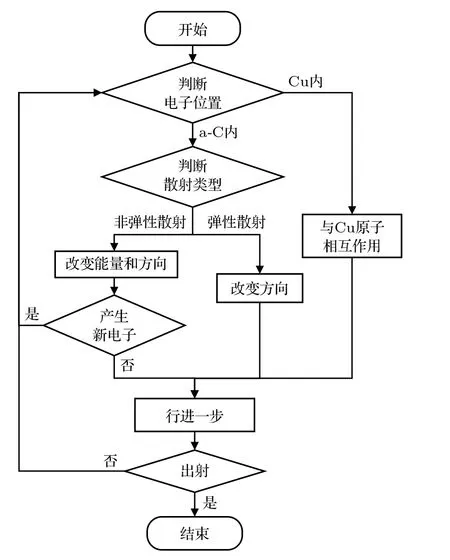
图2 基于MC 方法的a-C/Cu 二次电子发射模拟流程图Fig.2.Flow chart of secondary electron emission from a-C/Cu based on the MC method.

电子的单步自由程Sn可以通过一个均匀分布在[0,1)之间的随机数R1获取:

其中λT为总平均自由程,有=(λel+λin)-1=ρσT,λel和λin分别表示弹性和非弹性散射的平均自由程.σT为总散射截面,ρ为材料的分子密度.

电子的散射类型可以用另一个[0,1)之间的随机数R2确定.如果当R2<λin/λT时,则进行弹性散射;否则进行非弹性散射.图3 展示了根据散射截面计算的在不同能量E0下,电子与Cu 和a-C 发生弹性和非弹性散射的概率P.

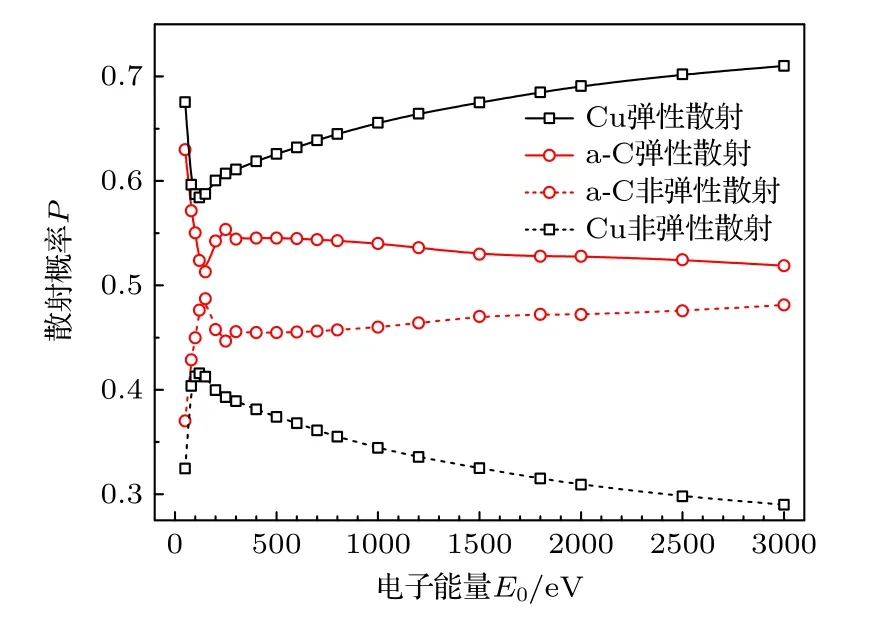
图3 电子与a-C 和Cu 原子的弹性和非弹性散射概率P 和电子能量E0 的关系Fig.3.Relationship between the elastic and inelastic scattering probability P of electron and a-C or Cu atoms and electron energy E0.

对于电子能量低于10 keV 的情况,用量子力学分波法求解Schrödinger 方程可以得到Mott 弹性散射截面,在物理意义上更为严格[23].然而,Mott散射微分截面 dφ/dΩ的数值解计算非常复杂,本文参考Czyzewski 等[24]的计算结果,利用查表与插值结合的方法预先获得在不同能量和散射角度下的Mott 散射截面值,弹性散射角度可通过随机数R3获得:

其中φ为散射截面;Ω为立体角;ϑ为两次散射事件间电子运动方向的夹角.

Penn 介电函数法是研究现代电子非弹性散射事件的标准方法,采用Penn 介电函数近似方法[25]计算非弹性散射微分截面和非弹性散射平均自由程.对于非弹性散射微分截面:

其中,EF为电子所处材料的费米能级.类似地,非弹性电子散射角度ϑ可通过R5获得

在进行非弹性散射后,原电子能量变为E0′=E0-∆E,新电子能量为Enew=∆E-EB,其中EB表示内壳层电子束缚能.

当电子遇到界面势垒时,一些电子会被反弹进入材料中,而另一些电子则能跨越界面势垒.以一维阶跃状势垒为例,能量为E1角度为β的电子在材料内部、势垒区和真空区的电子波函数都满足薛定谔方程,通过求解这三个区域的电子态密度,根据势垒两侧电子态密度之比,电子跨越高度为U0的界面势垒的概率可以由(6)式中的穿透系数Tin确定[16]:

其中,E1代表电子跨越界面势垒前的能量;β是电子运动方向与界面法线方向的夹角.只有当同时满足条件E1cos2β≥U0和Tin>R6(R6为(0,1]随机数)时,电子才能克服界面势垒.

如果电子无法克服界面势垒,则认为电子继续在当前材料内散射,其能量不会改变,但角度会变为β′′=π-β.

3 结果与讨论

3.1 实验验证

为了验证模型的可靠性,将计算结果与已报道的实验结果[28,29]进行对比.由于实验结果很容易受到表面状态和测试误差的影响,有必要对SEY进行归一化处理,相对SEY 记为δr=δ/δmax,Cu,其中δmax,Cu为Cu 的SEY 最大值.图4 显示了a-C薄膜厚度L分别为0,0.6 和2.1 nm 的a-C/Cu 的相对SEY 计算结果和实验结果的对比.由图4 可以看出,本模型的计算结果与实验结果非常接近,最大误差不超过12%,验证了模型的可靠性.

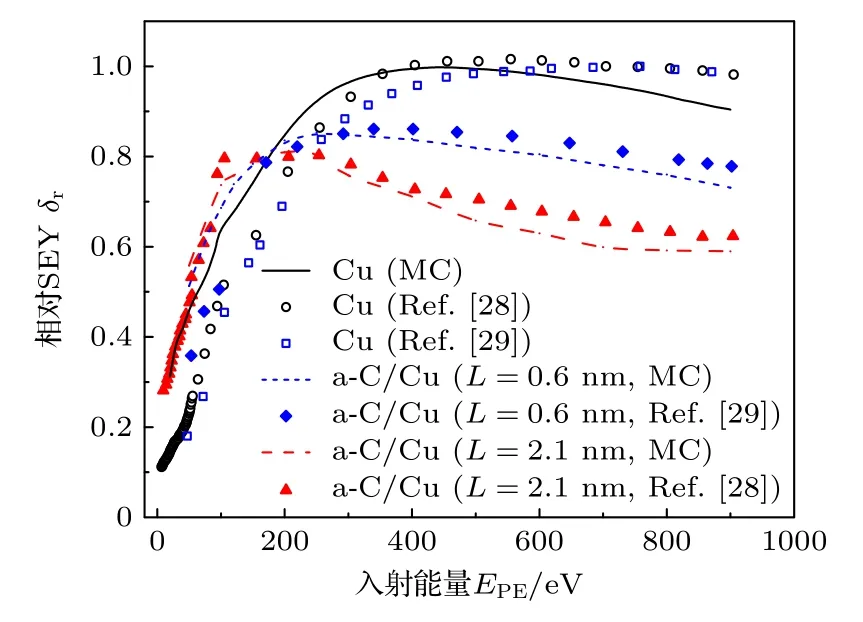
图4 MC 模拟结果与文献实验结果的对比Fig.4.Comparison of our MC simulation results and the reported experimental results.

3.2 a-C 薄膜厚度对SEY 的影响

为了系统探讨a-C 薄膜对Cu 的SEY 的影响,计算了不同薄膜厚度L的SEY 曲线,并与纯a-C材料的SEY 进行比较,如图5(a)所示.随着L从0 nm 增加到1.5 nm,SEY 最大值从1.14 降至0.93,但低能段的SEY 略微上升.然而,当L从1.5 nm增加到3 nm,SEY 最大值达到饱和,且与a-C 的SEY 最大值几乎重合.值得注意的是,当L≥1.5 nm时,SEY 曲线呈现出明显的第二峰,并且随着L的增加,第二峰减弱并消失,SEY 曲线从低能段到高能段逐渐与a-C 的重叠.此外,随着L从0 nm 增大至0.3 nm,第一临界能量从211 eV 降低至191 eV,对应第二临界能量从503 eV 增高至1020 eV.当L>0.3 nm时,SEY 峰值小于1,因此不会存在异常放电风险.图5(b)进一步展示了SEY 第一峰值δmax1和第二峰值δmax2以及它们对应的入射能量Emax1和Emax2随L的变化规律.

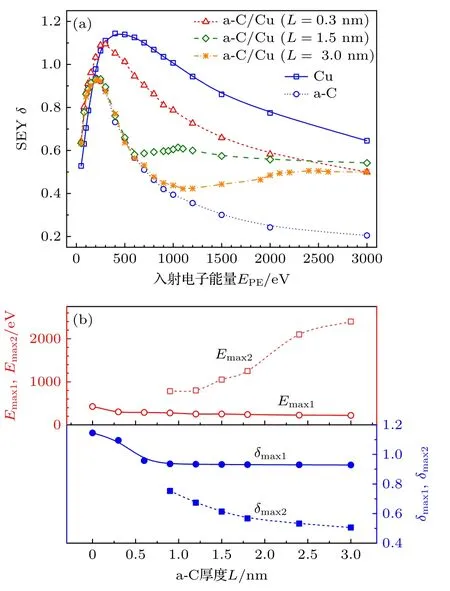
图5 厚度L 对SEY δ 的影响(a)不同L下,δ 与EPE的关系;(b) δmax1 ,δmax2 ,Emax1和Emax2 与L 的关系Fig.5.Effects of the thickness L on the SEY δ : (a) δ vs.EPE at different L;(b) δmax1 ,δmax2 ,Emax1 andEmax2 vs.L.

3.3 不同a-C 厚度的电子散射轨迹

MC 模拟能够还原电子在材料内部的散射过程,从微观层面解释双峰现象.图6(a)—(d)展示了1000个EPE=500 eV 的电子垂直入射到不同a-C 薄膜厚度的电子散射轨迹分布,即入射电子和电离电子在不同时刻的位置分布图,不同颜色代表电子的深度.随着L从0 nm 增大至2.4 nm,电子在材料内部的散射范围逐渐缩小,并且最可几深度(most probable depth,MPD)从Cu 转移至a-C中(图6(a)—(d)),其中MPD 表示与最大电子密度相对应的深度z.这意味着,当电子散射范围涉及两种材料时,SEY 特性表现为两者的合成,因此会有两个峰同时出现的情况.此外,较厚的a-C 会显著限制电子的散射范围,这是由于电子在a-C 中的非弹性散射概率大于在Cu 中的概率,大部分电子没有足够能量跨越表面势垒出射,导致SEY 降低.

图6 不同厚度L 下的电子散射轨迹分布及规律(a) L=0 nm;(b) L=0.9 nm;(c) L=1.5 nm;(d) L=2.4 nm;(e) MPD 和Pa-C 与L 的关系.图(a)—(d)中,灰色点线表示MPD 的位置,红色曲线表示归一化的电子密度分布Fig.6.Distribution and pattern of electron scattering trajectories with different L: (a) L=0;(b) L=0.9 nm;(c) L=1.5 nm;(d) L=2.4 nm;(e) MPD and Pa-C vs.L.In panels (a)–(d),the gray dot line represents the position of the MPD,and the red curve represents the normalized electron density distribution.

图6(e)进一步展示了MPD 和a-C 中电子数量比例Pa-C随a-C 厚度L的变化规律.定义Pa-C=Na-C/Ntotal,Na-C和Ntotal分别表示a-C 和a-C/Cu中的电子数量.当L从0 nm 增加到0.3 nm时,MPD 从1.46 迅速下降至0.24;进一步增大L会使MPD 增大,即向更深方向移动.此外,Pa-C随着L的增加而增加,当L≥ 0.6 nm时,Pa-C甚至大于0.5,意味着在a-C 内的电子数目超过在Cu 内的电子数.以上结果均表明a-C/Cu 界面势垒是阻止电子进入Cu 的关键因素之一.

3.4 入射角度对SEY 的影响

在实际应用中,大多数电子的入射角度与材料表面并不是垂直的.以L=1.5 nm 为例,图7(a)显示了不同入射角度θ下的a-C/Cu 的SEY 曲线.随着θ的增加,SEY 显著增大,并且第二峰也逐渐减弱至消失.此外,随着θ从30°增大至80°,第一临界能量从168 eV 降低至68 eV,对应第二临界能量从284 eV 增高至2840 eV.从图7(b)观察到δmax1和δmax2均呈指数增大,而Emax1和Emax2略微增加.为了定量分析第二峰的变化,定义了第二峰的高度δ∆和宽度E∆,如图7(c)所示.δ∆和E∆随着θ明显减小,直到θ≥70°时完全消失.这是因为θ越大,进入Cu 的电子比例减少,双峰现象就会减弱;其次,根据(6)式,电子在a-C/Cu 界面处的夹角β随θ的增大而增大,导致电子跨越界面势垒的概率降低.

图7 入射角度 θ 对SEY δ 的影响(a) 不同 θ下,δ与EPE 的关系;(b) δmax1 ,δmax2 ,Emax1和Emax2与θ 的关系;(c) δ∆ 和E∆与 θ 的关系.其中,图(c)中的内插图为 δ∆和E∆ 的示意图Fig.7.Effects of incident angle θ on the SEY δ : (a) δ vs.EPE at different θ ;(b) δmax1 ,δmax2 ,Emax1 and Emax2 vs.θ ;(c)δ∆and E∆ vs.θ .In panel (c),the interpolation diagram is a schematic diagram of δ∆ and E∆ .

3.5 不同入射角度的电子散射轨迹

图8(a)—(d)绘制了不同θ下的电子散射轨迹和沿深度z方向的电子密度分布.随着θ的增大,电子的散射范围显著缩小.同时,MPD 向表面方向移动.图8(e)定量地给出了MPD和Pa-C随着θ的变化规律.首先,Pa-C增大甚至接近0.97,意味着更多电子集中在a-C 区域内散射,Cu 对SEY 的影响逐渐减弱,因此双峰现象减弱;其次,MPD 减小表明电子散射位置向表面转移,更多电子仅在浅表层散射,此时电子更容易出射,SEY 随着θ的增大因而显著增大.

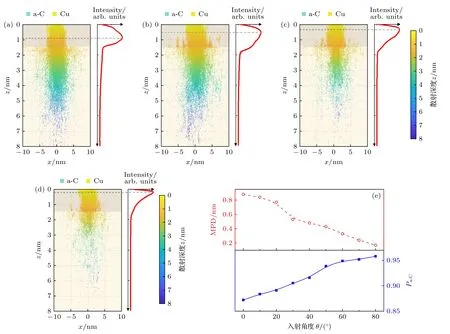
图8 不同入射角度 θ 下的电子的散射轨迹分布及规律(L=1.5 nm)(a) θ=0°;(b) θ=30°;(c) θ=60°;(d) θ=80°;(e) MPD和 Pa-C与θ 的关系.图(a)—(d)中,灰色点线表示MPD 的位置,红色曲线表示归一化的电子密度分布Fig.8.Distribution and pattern of electron scattering trajectories with different θ (L=1.5 nm): (a) θ=0°;(b) θ=30°;(c) θ=60°;(d) θ=80°;(e) the MPD and Pa-C vs.θ .In panels (a)–(d),the gray dot line represents the position of the MPD,and the red curve represents the normalized electron density distribution.

3.6 二次电子能量分布

二次电子能量分布(secondary electron spectrum,SES)包含了更丰富的表面信息,是表征二次电子发射的另一个重要参数[30,31].为此,图9 展示了EPE=500 eV 的电子束垂直照射不同厚度a-C薄膜的本征SES 与其半峰宽(full width at half maximum,FWHM)和最可几能量(most probable energy,MPE)的变化情况.随L的增加,SES 的本征峰逐渐降低,并向a-C 的靠拢,并且MPE 向高能段移动,FWHM 展宽.可见a-C 会使MPE 和FWHM 显著增大,表明a-C 薄膜会导致电子发生更频繁的非弹性碰撞,从而损失能量,导致低能电子比例减少,MPE 增大及FWHM 向高能段展宽.

图9 L 对SES 的影响(a) 不同L 下的SES;(b) MPE 和FWHM 与L 的关系Fig.9.Effects of L on the SES: (a) SES curves with different L;(b) MPE and FWHM vs.L.

4 结论

本文开发了一种a-C/Cu 双层材料的二次电子发射MC 数值模型,用于研究a-C 薄膜对Cu 的二次电子发射的影响.其中,电子与目标原子之间的弹性散射和非弹性散射过程分别采用Mott 理论和Penn 介电函数模型描述.为了精确重现电子在a-C/Cu 内的散射过程,模型还考虑了a-C 引起的功函数的变化以及电子在a-C/Cu 界面及真空/a-C界面处的多次散射过程.基于本模型的计算结果,得到以下结论.

1) a-C 薄膜可以使Cu 的SEY 最大值从1.14降低到0.93.这是因为a-C 薄膜能够通过更多次的非弹性散射事件降低电子的能量,并且a-C/Cu 界面能够限制电子的散射范围,从而降低SEY.

2) 当a-C 薄膜厚度大于0.9 nm时,SEY 曲线开始呈现双峰现象.然而,继续增加a-C 薄膜厚度,第二峰减弱并向高能段移动.通过增加a-C 薄膜厚度和电子入射角度,均会使第二峰减弱甚至消失.

3) 双峰现象是由电子在两种不同材料中的散射引起的,表现为两种材料SEY 特性的重合.较厚的a-C 薄膜或较大的电子入射角度都会将更多电子限制在a-C 薄膜内,减弱SEY 的第二峰.

本文提出的模型有助于从微观层面理解多层结构的二次电子发射特性,对于选择合适的薄膜厚度以抑制二次电子发射,以及避免双峰现象引起的异常放电具有重要的理论指导意义.