垂直管内高质量流速超临界CO2换热特性

朱兵国，巩楷刚，彭斌

（兰州理工大学机电工程学院，甘肃 兰州 730050）

近年来，我国一直贯彻新发展理念、推动高质量发展，积极参与国际社会碳减排，顺应全球绿色低碳发展潮流，制定了“2030 年前碳排放达峰”行动方案，提出了“2060 年前实现碳中和”远景目标。超临界二氧化碳（S-CO2）循环发电技术由于其在系统紧凑性、高效率、适用性、灵活性等方面具有无可比拟的优势得到了国际上的广泛关注，成为顺应时代背景的热点课题[1-3]。此外，在“双碳”任务的背景下，探索先进的发电技术能够有效地提升能源利用率、构建低碳和清洁安全的能源体系，而S-CO2动力循环发电系统是有效提升能源利用率的先进技术之一[4-5]。

Jiang等[6-7]对S-CO2在加热微型管内的对流传热特性进行了一系列实验和数值模拟研究，重点阐述了运行参数、浮升力及流动加速效应等对微型加热管内S-CO2传热的影响，结果表明：S-CO2传热受入口温度、运行压力、热流密度、管径以及质量流速等参数的影响较大。刘生晖等[8]开展了竖直圆管内S-CO2强迫对流传热特性实验研究，实验结果表明：在S-CO2在竖直向上流动中，由于浮升力增强使得S-CO2从强迫对流传热过渡至混合对流传热，最后发展为自然对流传热，传热能力也由弱化逐渐到恢复直至强化；然而流动加速效应则抑制S-CO2传热能力。Gökkaya 等[9]开展了0.509mm 微管内SCO2向上和向下流的对流传热实验，结果表明：不论向上还是向下流动，S-CO2对流传热特性主要受浮升力影响。Guo 等[10]对超临界压力CO2在垂直加热管内的对流传热特性进行了数值模拟，建立了变湍流普朗特数SSTk-ω湍流模型，分析了拟临界点附近的质量流速、热流密度、管径、入口温度和浮升力对超临界压力CO2传热的影响规律。王柯等[11]对S-CO2在垂直微细管道内的传热特性进行了数值模拟，发现增大质量流速可以减小壁面边界层厚度，从而强化换热；此外由于重力和浮升力作用的综合影响，导致流动方向可以影响S-CO2传热性能。Kline等[12]实验研究了超临界压力CO2在垂直向上流动加热管中的对流传热特性，发现传热恶化的发生与入口温度有密切关系。当入口温度小于拟临界温度，内壁温度将会急剧升高，即发生传热恶化现象；当入口温度大于拟临界温度，内壁温度单调上升，则属于正常传热现象。吴新明等[13]对S-CO2在圆管内流动时的压降和摩擦系数进行了实验研究，发现摩擦压降随着质量流速和压力的增加而显著增加，而热流密度对摩擦压降的影响较小。王乃心等[14]对S-CO2在不同管道内的对流传热特性试验进展做了研究，归纳得出：垂直管道内与异形管道内的S-CO2对流传热特性的研究相比水平管内更加匮乏。

综上所述，尽管目前研究者们对S-CO2对流换热进行了大量研究，但这些研究都是在中低质量流速下进行的，传热特性受浮升力的影响较大，而文献[15-16]中可以找到不一致的结果，浮升力和流动加速效应的评判标准并不能广泛适用。此外，在实际工程中，例如S-CO2燃煤发电循环，由于热力学要求，S-CO2燃煤发电系统的循环流量是水蒸气机组的6～8倍[5]，导致S-CO2锅炉正常的运行工况参数大部分是处于高质量流速的条件下。朱兵国[17]建立了超高参数CO2对流传热实验系统，弥补了实验数据的不足，但质量流速也主要集中在1000kg/(m2·s）附近，由于随着质量流速的提高，实验需要的加热功率在不断增大，对实验条件提出了更高的要求，从而缺乏高质量流速条件下管内S-CO2对流传热特性的实验研究。数值模拟作为超临界流动传热研究的重要手段，不仅可以弥补实验的不足还可以获取到详细的内部流场信息。因此，本文因利用数值模拟开展了高质量流速条件下S-CO2在不同管道内的对流传热特性的研究，分析了不同参数对传热的影响，通过内部流场信息来揭示换热机理，建立适用于高质量流速条件下的新型传热关联式，此项工作也将更好地帮助研究者理解超临界流体传热机理，对S-CO2循环发电动系统的设计也具有重要意义。

1 模型和方法

1.1 物理模型

图1展示了本文研究的垂直圆管物理模型，管长为2800mm，包含入口绝热段L1=500mm、有效加热段Lh=2000mm和出口绝热段L2=300mm，内径din=10mm。其中入口绝热段是为了确保CO2流至加热段处已经充分发展，避免入口效应对数值模拟产生影响；出口绝热段是为了防止回流影响计算精度。流动方向沿z轴的正方向，重力方向与流动方向相反。本文主要研究S-CO2在垂直圆管内对流换热的特性，管壁厚度并不会影响流体域的研究，故忽略管壁厚度。

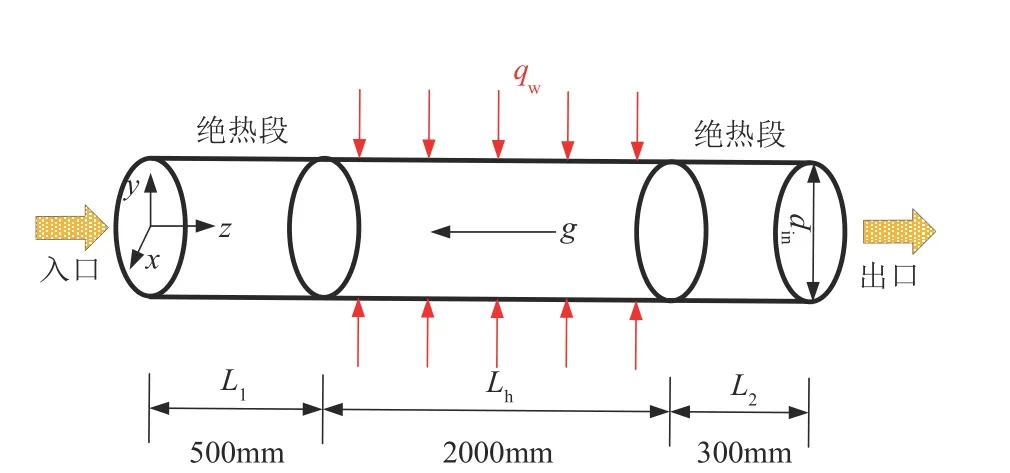
图1 物理模型

1.2 数值方法

众所周知，网格对其热物性的捕捉至关重要，也是探索S-CO2管内对流传热特性的关键。因此，为了很好地捕捉到剧烈变化的热物性引起的管内S-CO2复杂流动传热特性，本文对靠近壁面的区域网格进行了加密处理。已有研究表明在超临界流体流动传热数值计算中，对SSTk-ω湍流模型，流体域内靠近壁面第一层网格量纲为1高度y+需满足y+＜1[18]，来保证低雷诺数湍流模型的计算要求。

基于压力求解器求解控制方程，采用有限体积法对控制方程离散，离散格式采用二阶迎风算法，对压力速度耦合方程采用SIMPLEC 算法求解。能量项的亚松弛因子设定为0.85，其余保持默认值。为了获取到准确的CO2物性，计算过程中采用NIST实际气体模型。当质量方程和动量方程的最大残差值小于10-5、能量方程方程的残差值小于10-6且内壁温度不随迭代次数变化时认为计算收敛。质量守恒方程、动量守恒方程和能量守恒方程[19]在直角坐标系下分别表示为式(1)～式(3)。

质量守恒方程

式中，u为速度矢量，m/s；ρ表示密度，kg/m3；μ为黏度系数，Pa·s；h为比焓，kJ/kg；重力加速度g取9.8m/s2，Prt为湍流普朗特数；下角标i、j取1、2、3 时分别代表x、y、z三个不同的方向。

为了更好地阐述S-CO2管内对流换热特性，则必定需要管内S-CO2详细的对流传热信息，而选用合适的湍流模型是数值模拟计算的关键，因此本文基于众多研究者[19-21]对湍流模型（Standardk-ε、RNGk-ε、AKN、YS、LS、AB 和SSTk-ω）的研究基础上开展了对比试验，对不同的湍流模型进行了评估及选取。

关于Standardk-ε、RNGk-ε、AKN、YS、LS、AB 和SSTk-ω湍流模型输运方程表达式及相关常数项和函数项详细信息可参考文献[19]。

截面主流温度Tb和主流焓值ib分别定义为式(4)和式(5)。

传热系数h表示为式(6)。

式中，Tw为内壁温度，℃；Tb为主流温度，℃；A为垂直圆管流体域截面面积，m2；qw为壁面热流密度，kW/m2；i为焓值，kJ/kg；cp为定压比热容，kJ/(kg·℃)。

2 结果与讨论

2.1 湍流模型的优选

图2 展示了在压力p=8.221MPa、质量流速G=1001.5kg/(m2·s)和热流qw=244.33kW/m2的恶化工况条件下，采用七种不同的湍流模型进行数值模拟计算，预测垂直加热管内S-CO2的对流传热特性。通过与文献[22]的实验数据对比，由图2 不难看出七种湍流模型均能预测加热条件下S-CO2管内传热恶化的发生，且恶化点全都发生在拟临界焓值之前。但AKN、YS 和AB 模型明显将壁温预测过高，而LS、Standardk-ε、RNGk-ε和SSTk-ω均较好地预测恶化温度，但在恶化点前LS、Standardk-ε和RNGk-ε均低估了实验测量壁温，在拟临界焓值后同样也低估了实验测量壁温，仅有 SSTk-ω湍流模型预测的壁温与实验数据几乎重合，趋势也几乎一致。

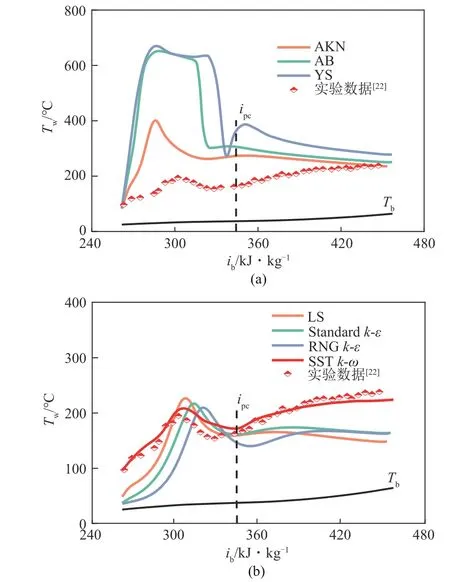
图2 不同湍流模型计算结果与实验数据对比[p=8.221MPa，G=1001.5kg/(m2·s)，qw=244.33kW/m2]

2.2 网格独立性验证及模型验证

网格数量过多将会浪费计算资源，过少则将会导致不能够很好地捕捉物性信息，因此选择合适的网格数量不仅有利于提高计算效率还可以保证计算精度。故本文对圆管网格划分进行了网格独立性验证，如图3 所示，采用四种网格节点数不同的模型进行了网格独立性验证。不难看出当网格中的节点总数大于250 万时，随着节点总数的增加，计算结果没有显著的偏差。在当前研究中，因此最终确定网格节点总数为250 万个。由前文可知，SSTk-ω湍流模型可以很好地预测SCO2管内对流传热规律，为进一步验证湍流模型的可靠性和准确性，选用文献[17]中的恶化工况及正常工况，建立相同的物理模型，对其数值模拟结果与实验结果进行了比较。如图4 所示，数值计算结果与实验结果吻合良好。因此，该模型可以用于数值模拟计算高质量流速条件下均匀加热管内S-CO2对流传热特性。

图3 网格独立性验证[p=8MPa，G=1500kg/(m2·s)，qw=400kW/m2，Tin=20℃]

图4 数值模拟计算与实验数据的比较

2.3 运行条件对高质量流速S-CO2 管内换热的影响

2.3.1 入口温度

图5 展示了压力p=8MPa、质量流速G=1500kg/(m2·s)和热流密度qw=400kW/m2的工况条件下入口温度对内壁温度的影响。如图5 所示，在相同的压力、热流密度和质量流速下，当入口温度低于拟临界温度时，在拟临界点之前观察到显著的温度峰值，这表明发生了传热恶化（HTD）。此外，随着入口温度Tin的增加，壁温的峰值向出口高焓值区移动，当入口温度高于拟临界温度时，壁温单调增加。从上述观察结果可以看出，在高质量流速和高热流密度的条件下，超临界压力下的传热特性受到入口温度的显著影响，而HTD 与入口温度也紧密相关。

图5 入口温度对壁温的影响数值模拟计算与实验数据的比较[p=8MPa，G=1500kg/(m2·s)，qw=400kW/m2]

2.3.2 运行压力

图6 展示了质量流速为G=1500kg/(m2·s)、入口温度Tin=25℃和qw=400kW/m2的工况条件下运行压力对壁温影响。从图6中可以观察到压力对传热特性的影响也非常重要，当压力为8MPa 时，壁温发生了突然上升又下降现象，产生了HTD；但当压力达到10MPa 时，壁温峰值明显降低，壁温峰值点也向出口方向移动；当压力达到15MPa 时，壁温则是随着主流焓值逐渐升高，HTD 现象并未发生。因此，在高质量流速和高热流密度条件下，增大压力可以抑制甚至消除HTD的发生。

图6 压力对壁温的影响[G=1000kg/(m2·s)，Tin=25℃，qw=400kW/m2]

2.3.3 热流密度

图7 展示了压力p=8MPa、质量流速G=2000kg/(m2·s)和入口温度流Tin=25℃的工况条件下热流密度对壁温的影响。当qw=200kW/m2时，壁温随主流焓值的增加平稳上升，并未发生壁面温度异常增大或减小，此现象属于正常传热。但是当qw=400kW/m2时，壁面温度出现了较小的峰值，即在高热流密度的条件下也发生了微弱的传热恶化现象。此外，一个有趣的现象是随着热流密度的增加，主流焓值ib也是逐渐增大，壁面温度也逐渐升高。总而言之，高质量流速条件的确有利于传热，但是当热流密度也较高时，HTD 依旧可能发生。

2.3.4 质量流速

图8展示了压力p=8MPa、热流密度qw=400kW/m2和 质 量 流 速G=1000～2500kg/(m2·s)下 质 量 流 速 对S-CO2传热的影响。如图8所示，在加热条件下，壁面温度受质量流速的影响较为显著，壁面温度随质量流量的增加反而大大降低。当G=1000kg/(m2·s)和1500kg/(m2·s)时壁面温度出现了显著的峰值，但在G=2500kg/(m2·s)时，壁面温度单调增加，表明较高的质量流速可以消除HTD并改善传热。

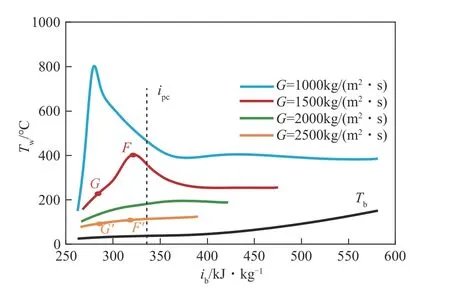
图8 质量流速对壁温的影响（p=8MPa，qw=400kW/m2，Tin=25℃）

2.4 传热机理

2.4.1 浮升力

浮升力是指当超临界流体流入加热管时，由于超临界流体在拟临界温度Tpc附近热物性变化剧烈，径向较小的温度差也会引起径向较大的密度差，径向密度差导致形成强浮升力，浮升力改变近壁区流体流场的分布，进而影响剪切力和湍流动能等的分布，最终导致传热的异常现象。Jackson[23]提出了垂直管道中S-CO2浮升力效应开始的标准数Bu。Bu数可以利用式(7)和式(8)进行计算。

描述垂直管道浮升力效应的另一个标准数Bu*可以利用式(9)和式(10)进行计算[23]。

Jackson[23]提出，当Bu＞10-5时，浮升力对超临界流体传热有显著影响，但是当Bu＜10-5时，浮升力对传热的影响可以忽略不计。Jackson 等[24]认为，当Bu*＜5.6×10-7时，浮升力效应较弱，对S-CO2传热规律的影响很小。

在p=8MPa、qw=400kW/m2、G=1000～2500kg/(m2·s)时，研究了浮升力对S-CO2传热的影响。图9 显示了Bu和Bu*在不同质量流速下的变化。随着质量流 速 从1000kg/(m2·s)增 加 到2500kg/(m2·s)，Bu和Bu*明显下降。这表明浮升力的作用随着质量流速的增加而减弱。

图9 不同质量流速下的浮升力变化

更重要的是，在四种不同的质量流速下，只有G=1000kg/(m2·s)时，在低焓值区Bu＞10-5，其他则在整个焓区都小于10-5；对于Bu*而言，同样只有在低焓值区Bu*＞5.6×10-7。上述结果表明，当质量流速较高时，浮力效应对S-CO2传热的影响较小，浮升力不能很好地解释高质量流速下S-CO2管内传热机理。

2.4.2 流动加速效应

Mceligot等[25]提出了采用Kv来表征流动加速度效应，其中Kv的计算如式(11)。他们认为当Kv＜3×10-6时，则不考虑流动加速效应对S-CO2对流传热特性的影响。

在p=8MPa、qw=400kW/m2、G=1000～2500kg/(m2·s)时，研究了流动加速效应对S-CO2传热的影响。图10反映了不同质量流速下Kv随主流焓值变化的分布，不难观察到流动加速效应随质量流速的增加而减小，但是在四种不同质量流速下，在垂直圆管内的整个主流焓区，Kv均小于3×10-6，说明高质量流速下流动加速效应对S-CO2传热也没有影响。

图10 不同质量流速下的流动加速效应的变化（p=8MPa，qw=400kW/m2，Tin=25℃）

2.4.3 类沸腾理论

浮升力和流动加速效应并不能很好地解释高质量流速下管内S-CO2的对流传热机理，因此为了更好地阐述高质量流速下管内S-CO2的对流传热特性，本文基于类沸腾理论，结合管内流体的热物性和流场分布，揭示高质量流速下S-CO2传热机理，阐述传热恶化原因。与亚临界流体并不相同，超临界流体类沸腾发生在一个有限的温度区间[T-,T+]，其中T-为相变起始温度，T+为相变终止温度。T-和T+可以由式(12)～式(14)确定[26]。

式中，cp,L为类液相的参考比热容，取为cp（p=pc，T=0.75Tc）；pc为临界压力；Tc为临界温度；TL为类液参考温度，取为0.75Tc；i0,L为类液参考焓，取为i（p=pc，T=0.75Tc）；cp,V为类气参考比热容，取为cp（p=0，T=Tc）；TV为类气参考温度，取为Tc；i0,V为类气参考焓，取为i（p=0，T=Tc）；cp,pc为拟临界点比热容；Tpc为拟临界温度；ipc为拟临界焓。

根据式(12)～式(14)可以求到两个交点，交点即为T-和T+的值。图11展示了超临界类沸腾传热模型，当超临界压力下的“过冷”流体流入垂直加热管时，如果温度Tw＜T-管内流体则为纯类液流体；如果温度T+＞Tw＞T-＞Tb，那么主流核心区为类液相，近壁区为类两相；当Tw＞T+时，近壁区为类气相，壁面附近形成一个类气层；而Tb＞T+时，管内流体为纯类气流体，而类液类气共存于有限温度区间[T-,T+]之间。

图11 超临界类沸腾传热模型

由于类气相具有像空气一样的低热导率，因此厚的类气层会导致较大的热阻，这将严重抑制热量从管壁到主流区的扩散，最终导致内壁温度急剧升高，发生HTD。然而，当入口温度高于拟临界温度时，主流为纯气态流体，传热特性符合单相对流传热，因此内壁温度随着主流焓值的增大单调升高。为了进一步探究造成传热恶化的原因，选取图7中的4个特征截面G、F和G'、F'进行分析，解释质量流速导致S-CO2传热产生差异的主要原因，阐述S-CO2对流传热机理。

图12展示了上特征横截面G、F和G'、F'处的热物性和湍流在径向上的详细分布，标记了T+的径向位置，类气膜厚度δ定义为T+径向位置到管内壁的距离。如图12 所示，特征横截面G处的类气膜厚度大于特征横截面G'处的类气体膜厚度，特征横截F处的类气膜厚度远大于特征横截F'处的厚度。换而言之，随着质量流速的增加，类气膜厚度逐渐减小。由于类气膜的低热导率和近壁区类气膜的低热吸收能力[图12(a)、(b)]，因此在特征截面G处和F处传热能力减弱。图12(c)展示了密度在径向方向上的分布，不难发现，近壁区主要被类气流体占据，而类液流体主要集中主流核心区。除了类气膜厚度和类气膜热物性外，近壁区的湍流动能对传热也有很大的影响。如图12(d)所示，近壁区的湍动能在高质量流速下比在低质量流速下高得多。即随着质量流速的增加，近壁区较薄的类气膜和更大的湍流动是传热增强的主要原因。综上所述，超临界S-CO2传热受类气膜厚度、类气膜热物性和近壁区湍流动能的影响较大。

图12 特征界面径向热物性和湍流的分布

2.5 高质量流速条件下传热关联式的建立

众多研究者通过热物性参数，将浮升力和流动加速效应因子等进行量纲为1 排列组合，对Dittus-Boelter 型关联式进行优化处理。Zhu 等[22]对亚临界沸腾和超临界传热进行了相似性分析，提出了超临界沸腾数SBO 用来预测传热恶化的起始点，验证了SBO 数的有效性。本文中存在大量的恶化数据，因此引入SBO 数拟合关联式。基于数值模拟及文献[17]数据建立超临界压力二氧化碳数据库，利用最小二乘法对各种无量纲数的排列组合进行选代寻优，得出了新的超临界压力二氧化碳传热关联式。式(15)和式(16)为拟合所采用的方程形式。

式中，cp为定压比热容，kJ/(kg·K)；μ为黏度，Pa·s；λ为热导率, W/(m·K)；i为焓值，kJ/kg；G为质量流速，kg/m2s；d为管直径，m；C为系数。

采用多变量线性回归方法确定C与n1～n5的系数，得到式(18)。

为了检验SBO 传热关联式与文献中广泛引用的五个关联式（表1）的精度，采取平均相对误差（eA）、平均绝对误差（eR）和均方根相对误差（eS）来定量评价传热关联式的预测精度。对于参数F，单个数据点的误差为式(19)。

表1 超临界传热关联式

图13 展示了已有的传热关联式计算所得的努塞尔数与实验确定的努塞尔数的分布。显然，D-B相关的预测精度是已有五个传热关联式中最差的，也说明了亚临界压力下的单相对流换热的传热关联式不能直接应用于超临界流体传热预测。图13(c)～(f)展示了一些研究者基于D-B 形式的传热关联式，采用物性比、浮升力因子和流动加速因子对其关联式进行了校正，提高了预测精度，但在高质量流速及恶化工况较多的条件下，精度依旧较差，在实际应用中不太能接受。而SBO 关联式则有一个非常小的eA=0.54%，并且平均绝对误差eR也仅为7.56%，这对于实际应用是可以接受的。与其他相关系数相比，均方根相对误差eS也是最小的。总之，SBO关联式给出了最好的预测精度。

图13 SBO关联式和其他关联式的比较

图13 展示了广泛引用的五个关联式预测的努塞尔数Nupre与实验确定的努塞尔数Nuexp的分布。如图13 所示，D-B 传热关联式的预测精度最差，图13(c)～(f)展示了众多研究者基于D-B 传热关联式，采用物性比、浮升力因子和流动加速因子对其修正进而提高了预测精度。可以观察到在高质量流速及恶化工况较多的条件下，这些关联式精度依旧较差，在实际工程应用中不太能接受。而SBO 关联式则有一个非常小的平均相对误差eA=0.54%，并且平均绝对误差eR也仅为7.56%，均方根相对误差eS也只有10.2%，SBO 关联式给出了最好的预测精度。

3 结论

采用SSTk-ω湍流模型研究了超临界压力CO2在高质量流量条件下内径为10mm的垂直加热管内的传热特性，分析讨论了入口温度、压力、热流密度、质量流速、浮升力和流动加速度对超临界压力CO2传热的影响。主要研究结果总结如下。

（1）通过与实验数据的对比，发现AKN、YS、AB、LS、Standardk-ε和RNGk-ε低雷诺数湍流模型对超临界压力CO2传热的预测精度很低，SSTk-ω低雷诺数湍流模型能很好地捕捉实验数据。表明SSTk-ω低雷诺数湍流模型对S-CO2流动换热数值计算具有可靠的适用性。

（2）HTD 的发生与入口温度密切相关。当入口温度小于拟临界温度时HTD 发生，而当入口温度大于拟临界温度时，壁面温度单调升高；提高压力和增大质量流速均可以延迟和抑制HTD。在高质量流速的条件下，浮升力和流动加速效应对SCO2的传热影响较小。从类气膜厚度的分布角度合理地解释了HTD发生的原因。

（3）引入超临界沸腾数SBO，基于数值模拟及文献数据建立超临界压力CO2数据库，利用最小二乘法对各种量纲为1 的数排列组合进行选代寻优，提出了新的SBO 传热关联式。与已有关联式相比，该关联式可以很好地预测高质量流速条件下S-CO2传热特性，其相对平均误差eA、绝对误差eR、均方根误差eS分别为0.54%、7.56%和10.2%。