油水环状流截面相含率超声衰减法测量

哈雯，杨杨，唐雨，曹頔，张超，杨斌

（1 上海理工大学能源与动力工程学院，上海 200093；2 上海市动力工程多相流动与传热重点实验室，上海 200093）

从世界能源现状分析，石油依然是当今世界的主导能源，随着原油开采进入高含水期，准确测量油井内油水两相流对原油产量评估、油井开发寿命预测、油井状态监测以及节能增效具有重要研究价值和现实意义[1]。其中油水环状流存在于诸多工程应用中，如稠油输送管线中采用油芯-水环流技术以降低流动阻力，减少运输成本[2]；在石油计量中，利用相分隔技术将油水两相流转化为油水环状流以降低两相流随机性和不稳定性，解决两相流测量精度难以保证的问题[3-4]；在相含率测量中，采用管道内径收缩的结构形成广义油水环状流流型，从而提高测量精度[5]。

目前油水两相流相含率在线测量方法包括电学测量法、微波测量法、射线法、超声法等多种技术。Chen等[6]利用电导探头的响应特征值估算了某垂直井油水两相流的相含率。Du等[7]使用多电极阵列电导传感器测量油水两相流的相含率。电导传感器的问题是其测量性能受到流体中电导率变化的显著影响。Dai 等[8]的研究关注了电容式传感器在油水两相流情况下的持水率测量。然而，电容法在高含水率情况下会受到短路效应的影响，从而影响测量结果的准确性。Liu等[9]提出一种透射式的微波谐振传感器来测量高含水油水两相流含水率。但这种传感器对噪声环境的敏感性限制了其在工业领域的广泛应用。Abbagoni等[10]基于伽马射线衰减模型推导油水两相流的相体积分数表达式，并进行了相应的实验测量。Sattari 等[11]结合伽马射线吸收技术和人工神经网络估算了油水两相流的相含率。射线法可实现较高精度的相含率测量，但其设备复杂、成本高，并对安全防护提出较高要求，因此在实际应用中受到一定的限制。

在众多测量方法中，超声法具备诸多优势，包括快速响应、结构简单、相对低成本、易于操作、高透明度、无辐射、不干扰流场且不受电导率影响等。因此，超声法在工业领域受到广泛的研究和关注。Shi 等[12]应用超声波传感器技术对水平管内油水流动进行了研究，建立了油水两相流相含率分布模型。Yu 等[13]通过建立多频衰减与液滴粒径分布的关系，基于衰减模型来估计油相体积分数。Chaudhuri 等[14]通过测量超声经过被测介质的传播速率与瞬时温度获得了油水两相流中的油相含率。Shao等[15]对上层油包水下层水包油、油水分层流流型进行仿真模拟，研究该流型超声衰减系数与油相含率之间的关系。Su等[16]的研究聚焦超声波测量油水两相流的相含率，当分散相含量较低时，超声衰减系数与相含率呈单调线性关系。Zhai等[17]采用脉冲透射超声波法测量低速高含水率条件下的相含率，得到含油率低于35%时，测量值和含油率呈较好的线性关系。尽管超声法在多相流的相含率测量领域中得到广泛应用，但针对油水环状流的超声测量方法研究还很少，而且油水环状流通常存在非理想情况，如偏心、变形等，这些因素可导致超声传播路径的变化，对基于超声衰减的测量方法产生重要影响。

针对超声衰减法测量油水环状流相含率问题，本文基于有限元方法，建立油水环状流仿真模型，选择超声波传感器尺寸及超声发射频率，采用超声衰减法研究油水环状流超声衰减特性，获得超声衰减系数与油相截面含率之间的关系，确定存在线性关系的测量范围，并分析非理想油水环状流的同心度和椭圆度对超声测量的影响，获得其在非理想环状流差别阈限±10%内的允许变化范围。本文将为超声衰减法测量油水两相流提供理论基础和重要参考。

1 基本原理

1.1 超声衰减法

油水两相流超声衰减机理可简化为黏性衰减和散射衰减的线性叠加。对于油水两相流，忽略热传导项，黏性衰减主要与介质本身特性有关，与油相含率有明显的线性相关性。而散射衰减分别受到油相大小、位置以及油相形状的影响，其传播过程中存在多种折射、衍射及反射的共同作用，散射衰减特性较为复杂[18-19]。

超声衰减法测量的基本原理是超声波发射端发出一定频率和强度的超声波，在油水两相流中穿过，经过油水两相的吸收、散射和反射等衰减机制后，到达超声波信号接收端[20]。在油水两相流中，定义超声衰减系数K如式(1)所示。

式中，P1和P2分别为超声波发射与接收端的声压，kPa；l为发射与接收端的距离，mm。

1.2 非理想环状流差别阈限

实际工程应用中，油水环状流的油相位置会存在偏心及变形等非理想情况[21]，而油核不同方向、不同偏心程度及变形都会对声场分布产生影响。考虑这类影响带来的测量误差，提出非理想环状流差别阈限E，见式(2)。

式中，K为理想环状流超声衰减系数，Np/m；K0为相同截面含油率下非理想环状流的超声衰减系数，Np/m。

由式(2)可知，E越小，非理想环状流的超声衰减系数越接近理想环状流的超声衰减系数，非理想环状流参数对超声衰减特性的影响越小。

1.3 油核同心度

研究油水环状流时，考虑油核偏心（图1）[22]对超声衰减的影响，引入同心度◎衡量圆心的偏移程度，定义同心度◎如式(3)，截面平均厚度式(4)。

图1 油核同心度分析示意图（单位：mm）

式中，Smax为截面的最大厚度，mm；Smin为截面的最小厚度，mm；S为截面的平均厚度，mm。其中，同心度◎=1时油核中心与管道的圆心重合。

1.4 油核椭圆度

研究油水环状流时，考虑油核变形（图2）[23]对超声衰减的影响，引入椭圆度OOR 衡量圆的变形程度，定义椭圆度OOR为式(5)。

图2 油核椭圆度分析示意图（单位：mm）

式中，D为椭圆的最大外径，mm；d为椭圆的最小外径，mm；R为标准圆的半径，R2=a×b，即R为椭圆长轴与短轴乘积的开平方，mm。

2 数值仿真

2.1 数值仿真模型

采用有限元方法，利用COMSOL 多物理场耦合仿真软件建立被测场二维几何剖分模型。几何模型见图3。设定管道内径为50mm，声压为 500kPa，单发单收的超声测量模式，主要仿真参数见表1。

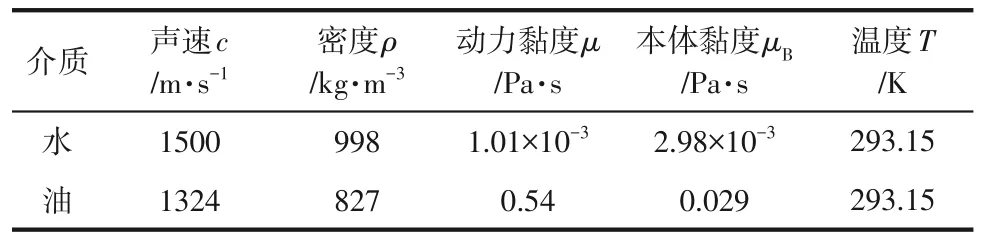
表1 油水环状流仿真参数表

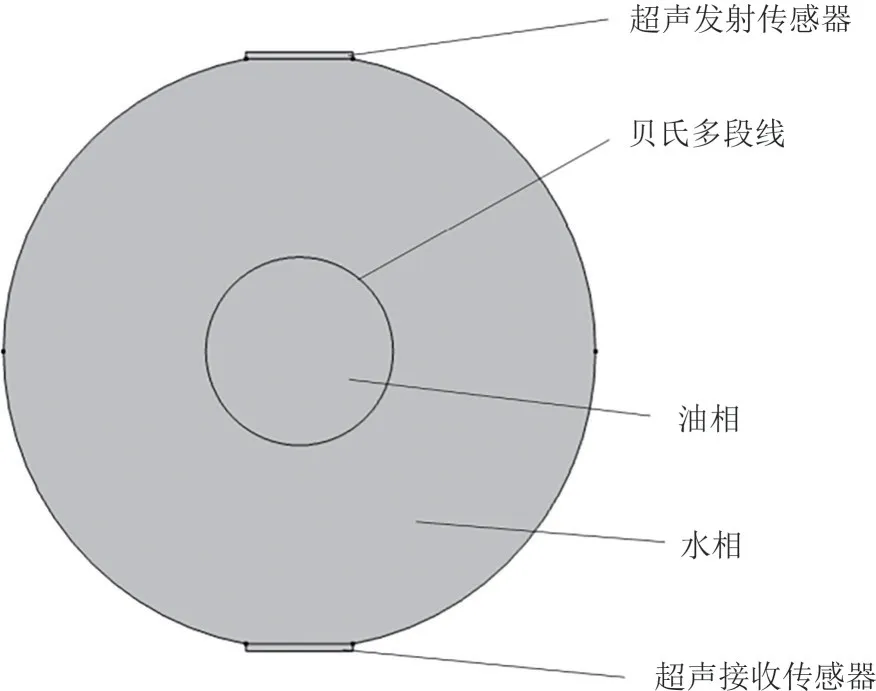
图3 油水环状流模型示意图

数值计算模型采用压力声学模型求解油水环状流油相大小、位置及形状不同情况下的声压分布。考虑流体的黏滞性，使用声速和密度的复值进行建模，引入波数keq得到频域研究中的非齐次亥姆霍兹方程[式(6)]。

式中，pt为总压力，kPa；keq为波数，1/m；ρc为密度的复值，kg/m3；Qm为连续性方程的质量源，1/s2；qd为动量方程的域力源，N/m3。

波数keq如式(7)计算。

式中，ω为角频率，rad/s；kz为面外波数，rad/m；cc为声速的复值，m/s。密度的复值ρc如式(8)计算。

式中，δ为运动黏度系数，m2/s；ρ为介质的密度，kg/m3；c为介质的声速。

声速的复值cc如式(9)计算。

黏度系数δ如式(10)计算。

式中，μ为流体的动力黏度，Pa·s；μB为流体的本体黏度，Pa·s。

总压力pt用式(11)计算。

式中，p为声压，kPa；pb为背景压力场，kPa。

在二维几何模型中，分析计算域对应的声场在面内传播，默认kz为0，简化为式(12)。

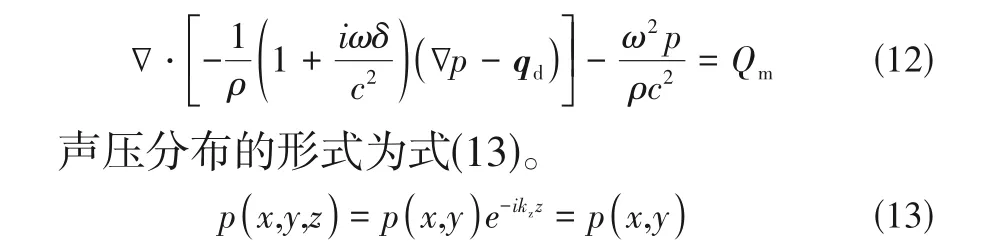
针对油水环状流模型建立自由剖分三角形划分网格结构，分别对不同相含率工况和超声激励频率进行网格无关性验证，用超声接收端监测接收声压值变化，结果如图4所示。由图4(a)可知，随着网格数增加，不同含油率工况下接收端声压值振荡变化，直至趋于稳定。由图4(b)可知，随着网格数增加，对于不同超声发射频率的工况下，超声接收端声压值会达到稳定值。综上，在不同相含率和超声发射频率的模拟中，当网格数超过39396个时，接收声压值逐渐保持稳定数值，不再随网格数的大小而变化。

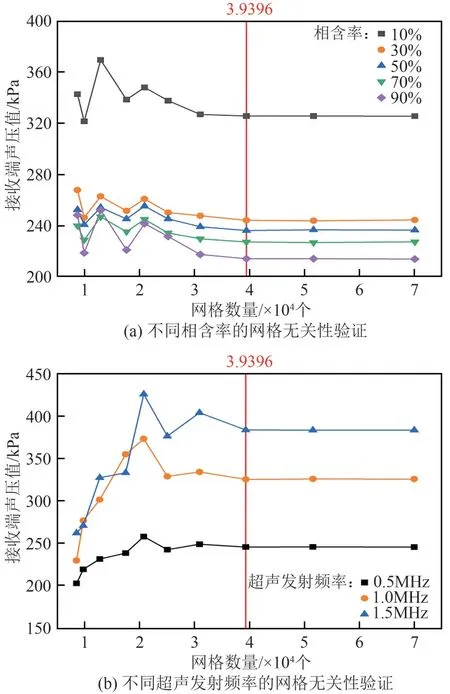
图4 网格无关性验证

2.2 超声传感器尺寸与发射频率选择

不同尺寸的超声传感器对声场分布有着不同程度的影响，工业上常用的换能器直径是3mm、6mm、9mm 以及12mm。对以上四种尺寸的换能器进行仿真模拟，设定模型介质为单相水，在(x,y)位置上放置油相液滴，用平均灵敏度和均匀性误差作为评价指标[24]，分析两指标对被测场域的影响，其中平均灵敏度参数越大表示传感器灵敏度越高，而均匀性误差参数越小表示传感器灵敏度场越均匀。超声灵敏度场分布由M个测试点(x,y)构成，坐标点(x,y)的灵敏度S(x,y)定义为式(14)。

式中，ΔSP(x,y)为超声传感器发射端与接收端的声压差，kPa；ΔSP(w)为被测场域满水的情况下，超声传感器发射端与接收端的声压差，kPa；ΔSP(o)为被测场域满油的情况下超声传感器发射端与接收端的声压差，kPa。

平均灵敏度Savg定义为式(15)。

式中，M为被测场域中测试点数量，个。

均匀性误差SVP定义为式(16)。

不同传感器尺寸的超声波声压分布与灵敏度场分布见图5，超声衰减系数与传感器尺寸之间的关系见图6，传感器尺寸与Savg、SVP 的关系见图7。根据声压分布、灵敏度场分布和数据结果可以得到：传感器尺寸对超声波波束特性和超声衰减过程产生一定的影响。由图5(a)可知，当传感器尺寸较小时，超声波波束的宽度较窄，超声波的发射和传播变得更分散，灵敏度场的高敏感区域主要集中在发射端，接收端声压强度较小，因此直径为3mm的传感器K较大，超声波在传播过程中衰减程度较大（图6）；由图5(b)～(d)可知，当传感器尺寸增大时，超声波波束逐渐变宽，超声波的传播更加集中，灵敏度场的高敏感区逐渐变宽，灵敏度逐渐增大，接收端的声压强度逐渐增大，因此超声波在传播过程中衰减程度变小，对于直径为12mm的传感器K最小（图6）。但并不是尺寸越大，超声衰减系数越小，测量效果就越好，由图7可以看出，随着传感器尺寸的增大，Savg逐渐增大，而SVP 呈现先下降后升高的趋势，在τ=6mm 时取得最小值，且此尺寸下的超声波在被测场域内传播具有较好的穿透性，传感器灵敏度场相对均匀。因此，综合考虑被测场对超声波波束宽度、接收端声压强度以及超声衰减的影响，选择超声传感器尺寸为6mm。

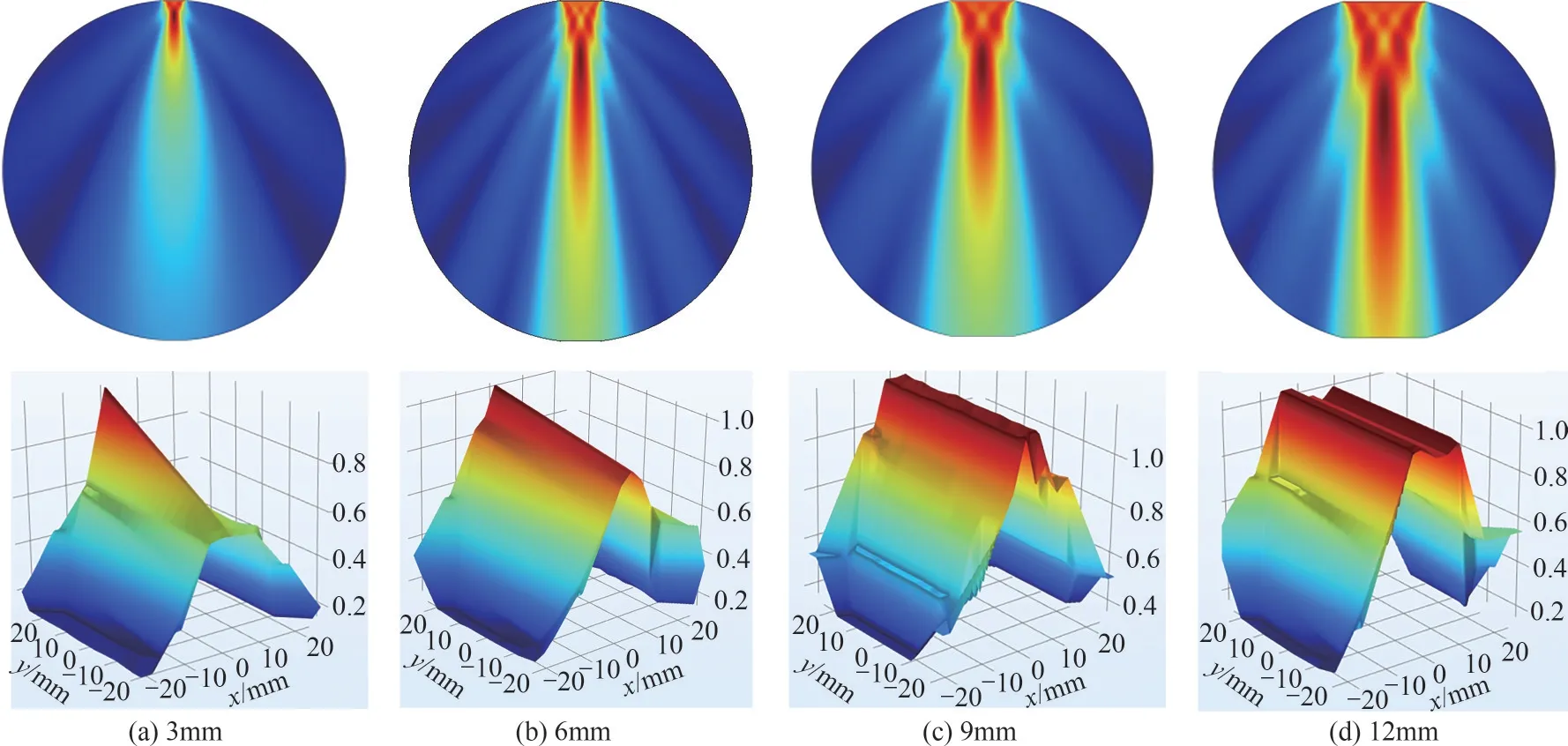
图5 不同传感器尺寸的声压分布与灵敏度场分布

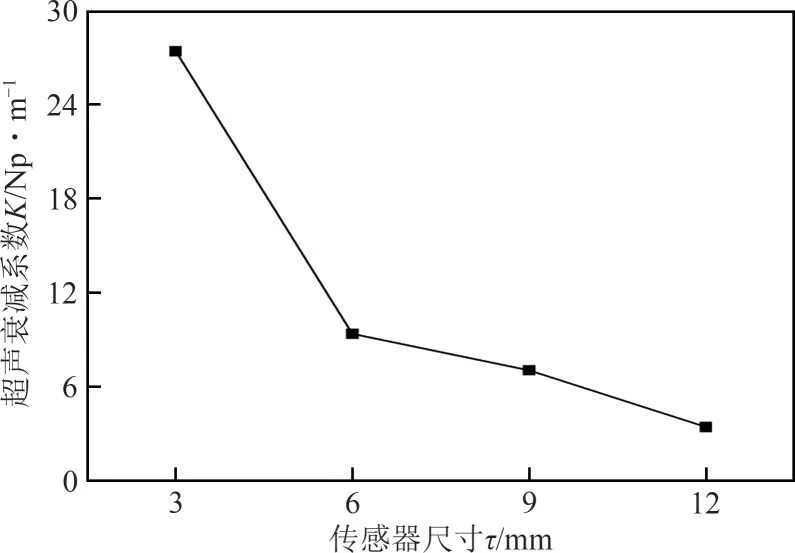
图6 传感器尺寸与超声衰减系数的对应关系

图7 传感器尺寸与Savg、SVP关系图

选定超声传感器尺寸6mm后，进一步选择超声发射频率。超声波用于油水两相流检测常用的中心发射频率为500kHz～2MHz[24]，选取其中4个频率点进行仿真模拟，得到不同超声发射频率的声压分布与灵敏度场分布如图8所示，超声衰减系数与发射频率的关系如图9所示。由图8可知，随着超声发射频率的增加，声压分布的声束越来越集中，超声波在被测场内传播具有较好的穿透性，有足够的超声波透射到接收端，超声衰减系数逐渐减小（图9）。超声发射端与接收端之间的声束范围内灵敏度较高，且呈现逐渐增大趋势，但不同频率的灵敏度场均匀性不同。灵敏度场对应的平均灵敏度及均匀性误差计算结果如图10 所示，随着超声发射频率增大，Savg逐渐增大，而SVP 呈现波动性变化的趋势。当超声发射频率为 1MHz 时，超声传感器灵敏度Savg足够大，被测场域灵敏度相对较高，而SVP 足够小，传感器灵敏度场相对均匀，因此选择1MHz的发射频率。

图8 不同超声发射频率的声压分布与灵敏度场分布

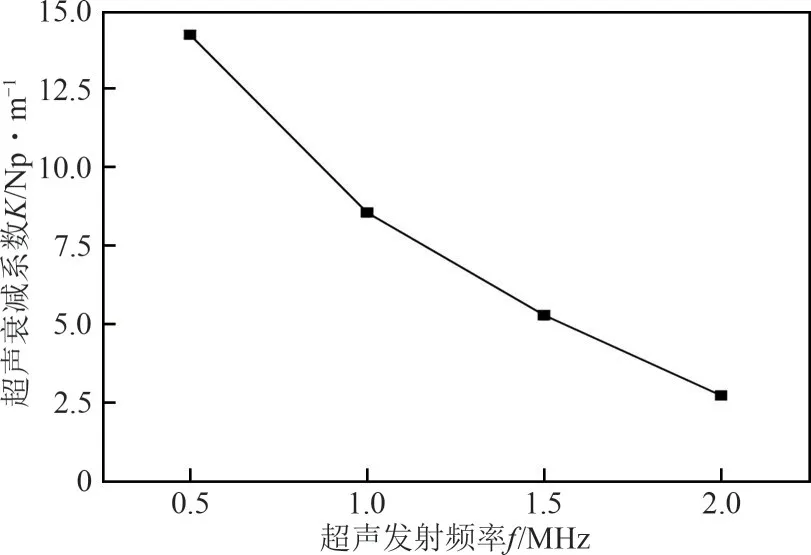
图9 超声发射频率与超声衰减系数的对应关系

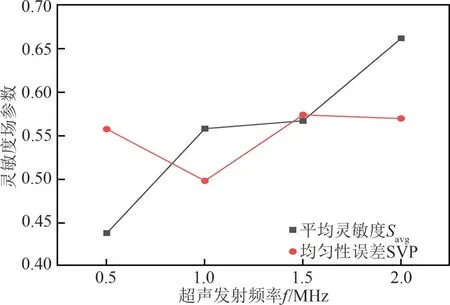
图10 超声发射频率与Savg、SVP关系图

3 结果与讨论

3.1 油相含率对超声衰减测量的影响

在研究油水环状流时，采用声学特性阻抗、超声波波长与超声指向角分析超声散射衰减特性。根据声学特性阻抗Z=ρc知，在油-水界面Zw＞Zo，当声波从油相传播到水相，入射角增大至arcsin(co/cw)≈62°时，折射角为90°，折射波沿界面传播；当入射角大于62°时，入射声能将全部反射到油相中。由超声波波长公式λ=c/f可知λ=3mm，当超声波传播至尺寸为λ～4λ的油核时，会绕过油核的边缘继续向前传播，即发生衍射。超声指向角φ指超声波声源发出的超声波束向外扩散的角度，定义见式(17)。

式中，λ为超声波的波长，mm；τ为超声传感器尺寸，mm。

油水环状流油相含率对超声衰减测量的影响研究结果见图11～图13。由于黏性衰减与油相含率有明显的线性相关性，因此如果只考虑黏性衰减，那么超声衰减系数会随着油相含率的增加而线性增加。比较图11(a)和图11(b)并结合图13可知，当含油率从3%升高到10%时，超声衰减系数不增反减，这是因为含油率为3%时，油核尺寸小于3λ，因此超声传播过程中发生衍射，对超声的传播途径产生汇集作用，使得超声接收端的信号很强，见图12(a)。从图11(b)和图11(c)并结合图13 可知，当含油率从10%升高到30%时，接收端声压逐渐减小，超声衰减系数会随着油相含率的增加而线性增加，说明此时黏性衰减占主要作用，散射衰减对线性度的影响不大。从图11(c)和图11(d)并结合图13 可知，当含油率从30%升高到40%时，超声衰减系数又发生了降低的趋势，比较图12(c)、(d)可以看出，由于油核的增大，使得相同角度的发射声波在油水界面上的入射角和折射角发生变化，并由于反射的作用，含油率为40%时声波的汇聚作用明显高于30%，使得接收端能够接收到更多的声波，超声衰减系数减小。从图11(d)和图11(e)并结合图13可知，随着油核的进一步增加，超声衰减系数又随着含油率的增加而呈现增加的趋势，这是因为当油核足够大时，比如图12(e)的含油率为50%时，在发射声波的指向角φ内，所有声束不再发生反射，黏性衰减再次起到主导作用。最后从超声衰减系数与含油率的变化结果关系图13 可得，截面含油率在0～100%范围内，超声衰减系数总体呈上升趋势，其中5%～30%范围内超声衰减系数与截面含油率呈良好的线性关系，拟合优度R2为0.978。

图11 油水环状流的声压分布

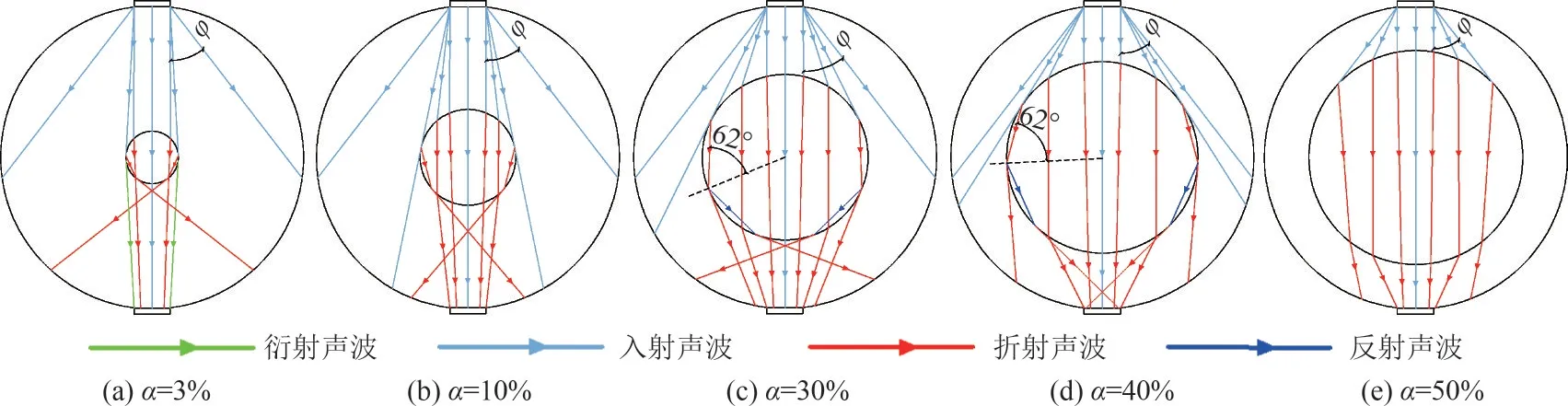
图12 油水环状流的声束分布

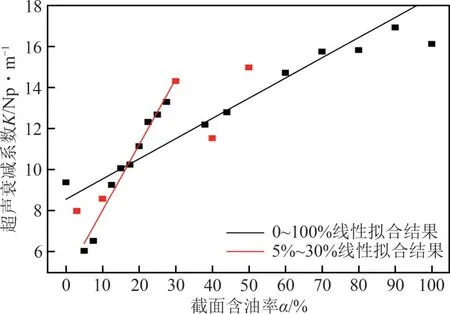
图13 油水环状流分布超声衰减特性

因此，对于理想油水环状流可利用5%～30%范围内超声衰减系数与截面含油率的线性关系对油水相含率进行准确测量。然而实际油水环状流会存在非理想环状流因素，使得利用理想环状流超声衰减法测量相含率发生测量误差，所以需要定量研究非理想环状流因素对于理想环状流超声衰减法的影响。

3.2 油核同心度对超声衰减的影响

非理想环状流因素中同心度是一典型因素，本文研究了油核同心度对油水环状流超声衰减的影响，结果见图14～图18。从图14分析可得，当θ一定，同心度越小，声场中部分透射声波随着界面的偏离反射和折射角度发生变化，致使超声传播方向发生偏折，使得超声接收端接收到的超声信号越少，超声衰减系数越大，这会导致θ一定时同心度越小、E越大的整体变化趋势，如图16所示。另外由图16(a)、(b)比较可知，截面含油率越大（油核直径越大），同心度对超声衰减的影响减小，E的增加减小。

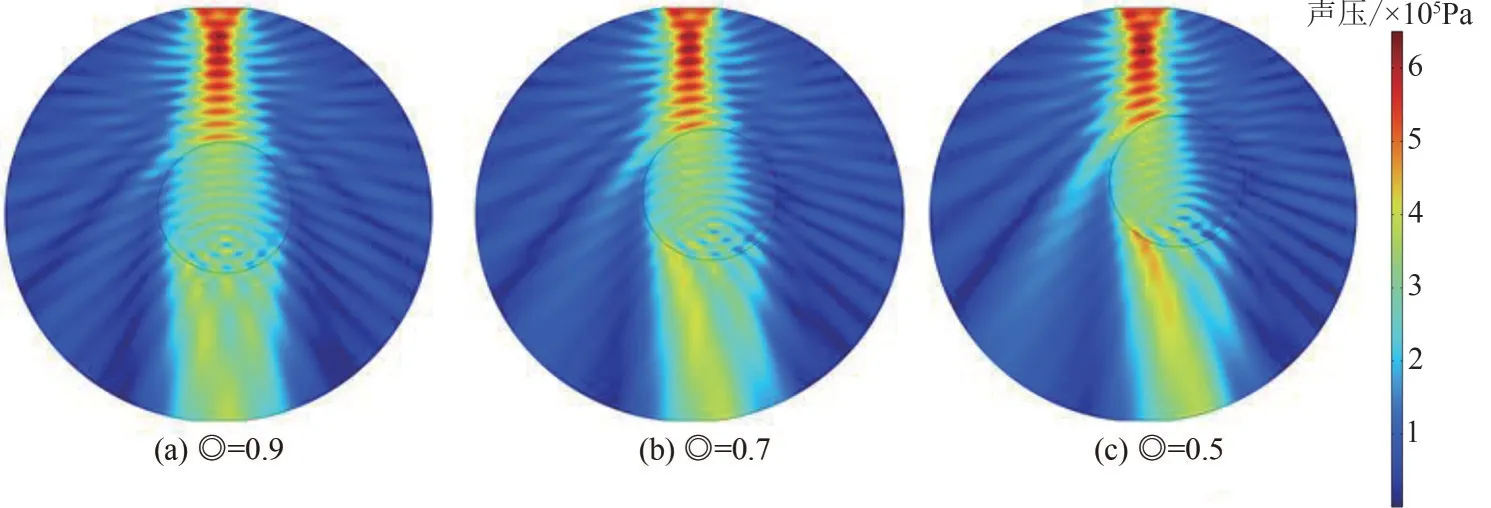
图14 含油率10%中θ=45°方向同心度声压分布

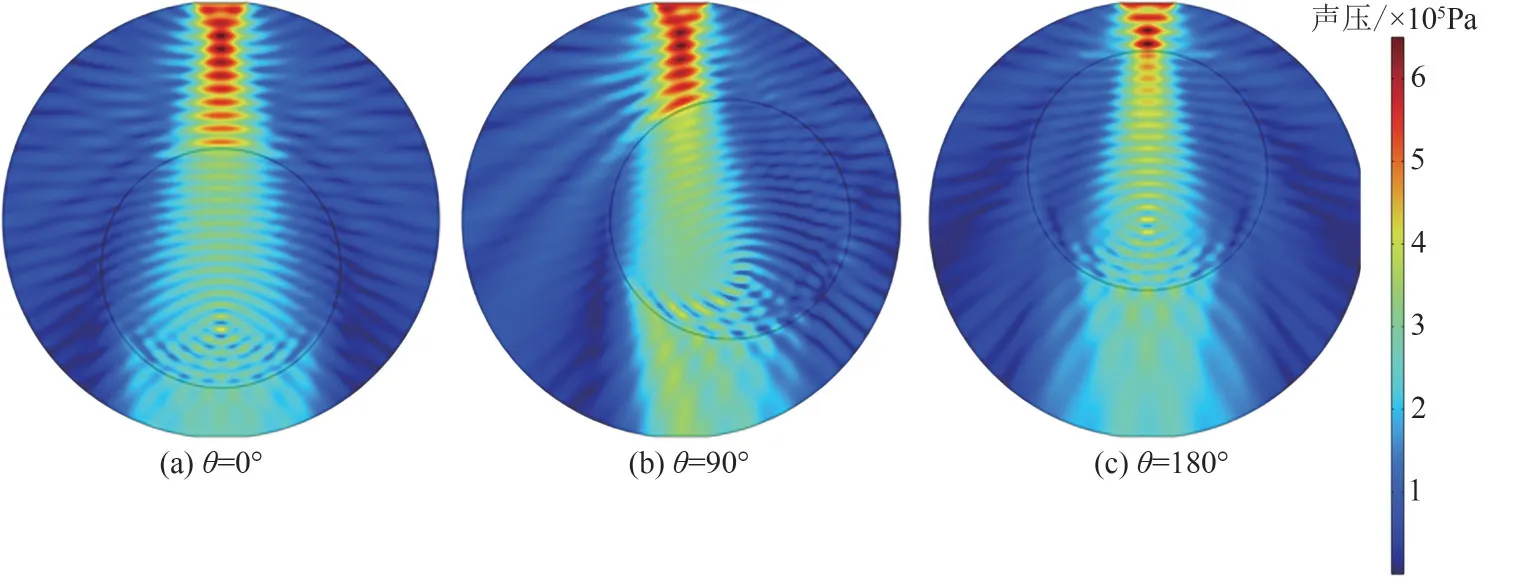
图15 含油率30%中同心度为0.5的声压分布

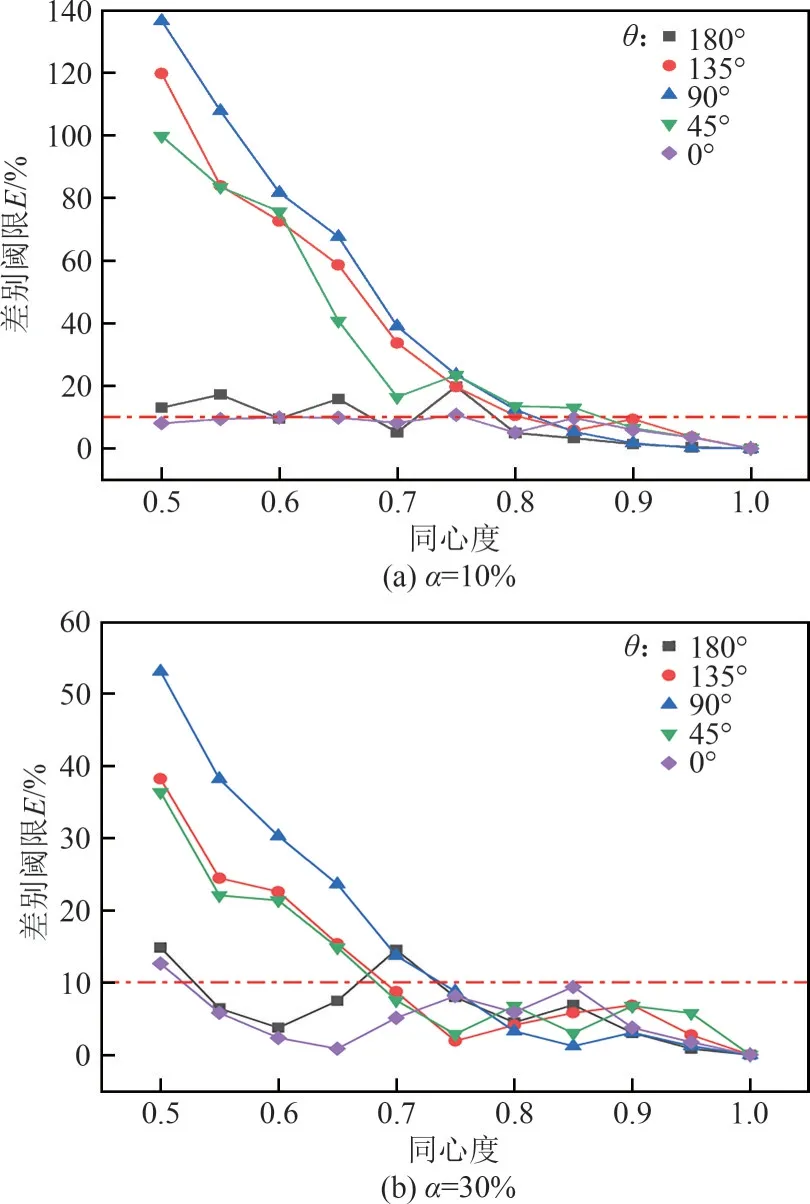
图16 不同同心度的差别阈限

从图15分析可得，当同心度一定、θ=90°时，油核相对于超声探头连线的偏移程度最大，导致接收端声压最弱，超声衰减系数最大，E最大，如图17所示。同时发现，θ=0°和θ=180°，或θ=45°和θ=135°的超声衰减特性并不相同。从图15(a)和图14(c)可以看出，θ=0°时超声散射后最终传播的方向更集中，接收端声压更大，因此E更小，如图17 所示。最后，不同截面含油率满足差别阈限在±10%以内的同心度最小值结果见图18，可以看出α在5%～30%内最小同心度为0.9，即当同心度大于0.9时，可保证α在5%～30%内的超声衰减系数与同心度为1（理想环状流）时的差距不大于±10%。

图17 不同θ的差别阈限

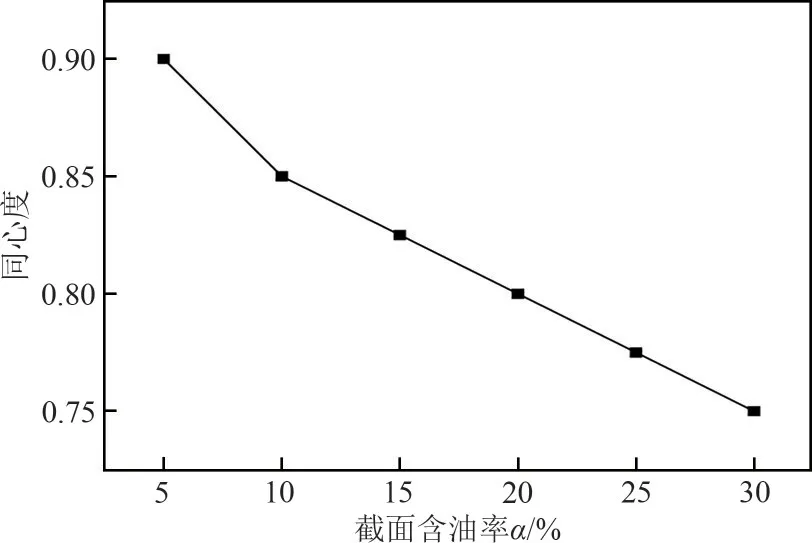
图18 差别阈限在±10%以内的同心度最小值

3.3 油核椭圆度对超声衰减的影响

非理想环状流因素中椭圆度是另一典型因素，本文同时研究了椭圆度对超声衰减的影响，结果见图19～图21。从图19 和图20 分析可得，在OOR=20%的情况下，当a/b＜1 时，油核呈中宽上下狭窄型，因油核上下两端较狭窄，超声波束集中，随着截面含油率的增加，经油核衰减进入超声接收端的超声信号减少，结合图21 可知，大部分情况下差别阈限E＜0，说明与理想环状流相比，超声衰减程度在各工况下普遍降低；当a/b＞1 时，油核呈中宽左右狭窄型，因油核中部宽，超声波束分散，部分超声波经油核左右两端界面折射，使得接收端接收到的超声信号强度整体降低，结合图21 可知，大部分情况下差别阈限E＞0，说明与理想环状流相比，超声衰减程度在各工况下普遍增加。由图21(a)、(b)比较可知，椭圆轴比越大，椭圆度对超声衰减的影响越小，满足差别阈限在±10%以内的椭圆度范围越大。同时发现截面含油率越大，椭圆度对超声衰减的影响越小，如α=30%可达到OOR＜27.5%。

图19 OOR=20%时不同含油率声压分布（a/b＜1）

图20 OOR=20%时不同含油率声压分布（a/b＞1）

图21(a)、(b)示出了满足差别阈限在±10%以内的椭圆度范围，由图可以看出，随着含油率降低，满足非理想环状流差别阈限在±10%以内的椭圆度范围减小，仅当OOR＜5%时能够忽略截面含油率5%～30%全范围内油核变形带来的超声衰减影响。

4 油水环状流静态实验

4.1 油相含率与超声衰减线性关系验证

为验证本文仿真实验模型的可行性，搭建如图22 所示油水环状流测量实验装置。实验参数设置与仿真模拟相同：采用管内径50mm的模具，管道中心放置壁厚1mm 的PVC 透明管来分离油水两相，并通过不同的管内径来控制油相含率。其中，截面含油率变化范围为5%～30%，油相采用工业白油，密度为827kg/m3，水相为自来水，密度为998kg/m3，超声传感器发射频率为1MHz，超声脉冲发射接收器触发并接收信号。

图22 油水环状流测量实验装置

由于超声激励电压信号与声压信号存在正比关系，即声压的变化会导致相应的电压信号变化，提取激励信号与透射衰减信号的峰峰值来计算超声衰减系数K*，由式(18)计算。

式中，V1和V2分别为超声波发射与接收信号的峰峰值，V。

由于PVC 透明管的存在会引起超声波的折射和反射，导致测量得到的超声衰减系数增加。因此本文通过测量纯水与放置PVC 透明管后纯水的超声衰减系数的差值，估计PVC 透明管对总衰减的贡献，得到PVC透明管的超声衰减系数KPVC，再通过式(19)进一步计算得到实际测量的油水超声衰减系数Ka。

式中，Ka为实际测量的油水超声衰减系数，Np/m；KPVC为PVC透明管的超声衰减系数，Np/m。

实验与仿真模拟测量的超声衰减系数随截面含油率变化的结果如图23 所示。可以发现：仿真模拟结果与实验结果在上升趋势上表现出一致性，超声衰减系数与截面含油率呈线性关系。由图23 可以看出，实验得到的超声衰减系数整体偏小，这是由于实验中管道是有一定壁厚的，且管道的声阻大于油水声阻，使得一部分超声波经管壁反射，引起了超声衰减系数的减小。

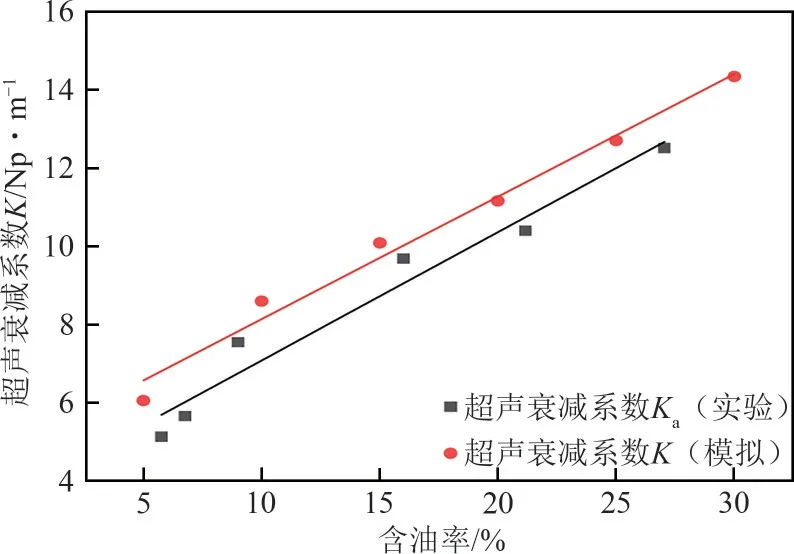
图23 油水环状流实验与模拟结果图

4.2 油核同心度影响实验验证

利用如图22 所示油水环状流测量实验装置同时也可对油核同心度模拟结果进行验证，截面含油率为5%～30%范围内的实验结果见图24～图26。可以看出：实验结果从趋势上与仿真模拟结果（图16～图18）能达到较好的吻合。不同截面含油率满足差别阈限在±10%以内的同心度最小值的实验和模拟结果如图26 所示，实验测量结果与仿真模拟结果的平均误差为1.36%，产生这一误差的主要原因在于仿真模拟和实验测量中超声衰减系数的差异。截面含油率为5%～30%范围内，实验测量的超声衰减系数结果整体偏小，根据式(2)可知，该实验结果会导致非理想环状流差别阈限的结果整体偏大，使得不同截面含油率满足差别阈限在±10%以内的同心度最小值变大，其中，α在5%～30%范围内满足差别阈限在±10%以内的最小同心度为0.913。

图25 不同θ的差别阈限实验结果

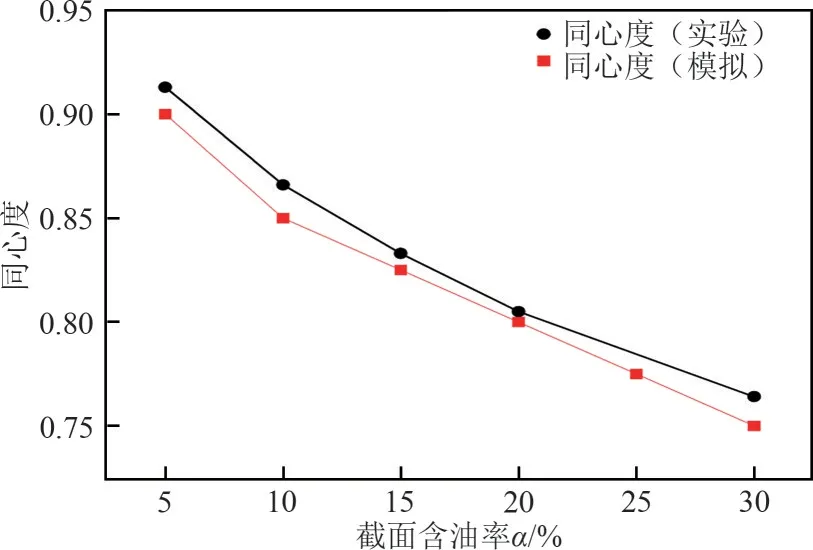
图26 差别阈限在±10%以内的同心度最小值

5 结论

本文针对油水环状流截面相含率测量问题，采用COMSOL 仿真软件建立油水环状流模型，获得了超声衰减系数与截面含油率线性关系的测量范围，并在此基础上进一步研究非理想环状流因素对超声衰减特性的影响，最后开展了油水环状流静态实验验证，得到以下结论。

（1）油水两相流超声衰减与黏性衰减和散射衰减密切相关，对于理想环状流，在5%～30%的含油率范围内，油水环状流的截面相含油率与超声衰减系数呈线性关系，为超声衰减法测量油水环状流的相含率提供了可行性依据。

（2）研究了油核偏心对超声衰减的影响特性，结果表明，同心度一定、θ=90°时，油核相对于超声探头连线的偏移程度最大，同时θ=0°和θ=180°，或θ=45°和θ=135°的超声衰减特性并不相同，截面含油率越大（油核直径越大），同心度对超声衰减的影响减小，当同心度大于0.913 时，可满足α在5%～30%范围内超声衰减系数与同心度为1（理想环状流）时的差距，即非理想环状流差别阈限不大于±10%。

（3）研究油核椭圆度对超声衰减的影响特性，结果表明，相同截面含油率下椭圆轴比a/b＞1 和a/b＜1 两种情况中超声衰减程度与理想环状流相比结果相反，截面含油率越大，椭圆度对超声衰减的影响越小。当OOR＜5%时能够满足截面含油率5%～30%内非理想环状流差别阈限在±10%以下。

（4）开展了油水环状流静态实验，实验结果表明，在理想环状流情况和油核存在偏心时，模拟与实验超声衰减系数结果随着截面含油率和同心度的变化具有相同的趋势，验证了本文超声模拟方法的可靠性。

符号说明

c,cc——分别为介质的声速、声速的复值，m/s

D——椭圆的最大外径，mm

d——椭圆的最小外径，mm

E——非理想环状流差别阈限，%

f——超声发射频率，MHz

K——理想环状流超声衰减系数，Np/m

K0——相同截面含油率下非理想环状流的超声衰减系数，Np/m

K*——实验油水环状流超声衰减系数，Np/m

Ka——实际测量的油水超声衰减系数，Np/m

KPVC——PVC管的超声衰减系数，Np/m

keq——波数，m-1

kz——面外波数，r/m

l——超声波发射端与接收端的距离，mm

M——被测场域中测试点数量，个

OOR——椭圆度，即用于衡量圆的变形程度，%

P1,P2——分别为超声波发射端与接收端的声压，kPa

p,pb,pt——分别为声压、背景压力场及总压力，kPa

Qm——单极域源，S-2

qd——偶极域源，N/m3

R——标准圆的半径，mm

S,Smax,Smin——分别为截面的平均厚度、最大厚度和最小厚度，mm

Savg——平均灵敏度

S(x,y)——坐标点(x,y)的灵敏度

SVP——均匀性误差

T——温度，K

V1,V2——超声波发射与接收信号的峰峰值，V

Z,Zw,Zo——分别为介质、水、油的声学特性阻抗，kg/(m2·s)

ρ,ρc——分别为介质的密度和密度的复值，kg/m3

α——油相截面含率，%

ω——角频率，r/s

δ——运动黏度系数，m2/s

μ,μB——分别为流体的动力黏度和本体黏度，Pa·s

λ——超声波的波长，mm

τ——超声波传感器尺寸，mm

φ——超声指向角，指超声波声源发出的超声波束向外扩散的角度，(°)

ΔSP(x,y)——超声传感器发射端与接收端的声压差，kPa

ΔSP(w)——被测场域满水的情况下，超声传感器发射端与接收端的声压差，kPa

ΔSP(o)——被测场域满油的情况下，超声传感器发射端与接收端的声压差，kPa

◎——同心度，即用于衡量圆心的偏移程度

下角标

avg——平均值

c——复值量

max——最大值

min——最小值

o——油相

w——水相