基于EMD的螺旋输送机叶片运动速度静电检测方法

王超，曹辉，马国纪，叶佳敏，纪学玲

（1 天津大学电气自动化与信息工程学院，天津 30072；2 天津大学未来技术学院，天津 30072）

螺旋输送机是一种依靠螺旋叶片旋转推动管内物料运动的机械，具有结构简单、密封性好和便于封闭运输等优点，被广泛应用于化工、冶金、粮食和运输等领域中的物料运输[1]。

螺旋输送机中叶片的运动对输送状态有直接的影响[2-3]。但其往往采用封闭运输，且运行环境恶劣，目前仍缺少有效的检测手段。经过长时间的运行后，常出现螺旋叶片变形，螺距和螺旋角改变，甚至发生断轴事故[4-5]。通过实时检测螺旋叶片的运动速度，可及时获得螺旋输送机的运行状态。

螺旋叶片带动物料运动，运动的物料在碰撞、摩擦以及破碎等过程中产生电荷。通过静电感应原理检测颗粒荷电状态，进而结合互相关技术实现颗粒速度的测量，已经在气力输送领域获得了成功应用[6-7]。本文以螺旋叶片的运动状态检测为目标，设计了静电传感器，针对静电信号噪声干扰严重的问题，提出了基于经验模态分解（empirical mode decomposition，EMD）的静电信号滤波处理方法。

1 研究方法

1.1 螺旋输送实验装置与静电传感器设计

设计了螺旋输送实验装置，如图1所示。实验装置采用由下到上的垂直输送，通过调速电机控制转速。

图1 螺旋输送实验装置

螺旋叶片与静电传感器的结构尺寸如图2 所示。螺旋叶片为双螺旋结构，由不锈钢材料制成，螺旋叶片螺距为95mm，螺旋叶片直径为90mm，螺杆直径30mm，管道直径100mm。

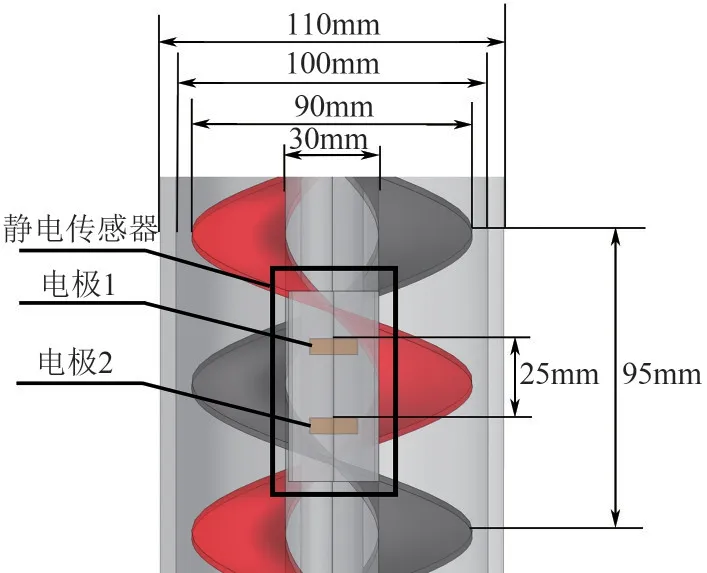
图2 螺旋叶片与静电传感器的结构尺寸

静电传感器的两个电极间距为25mm，电极长15mm，宽5mm，厚2mm。在螺旋输送机的管道壁上开孔，将静电传感器插入，电极所在面与管道内壁平齐。

1.2 静电相关速度计算

1.2.1 静电信号检测与处理

静电检测系统如图3所示，由信号调理、数据采集和数据处理单元组成。其中，信号调理电路采用电流放大电路[8]；数据采集和数据处理单元使用简仪公司的PXIe 控制器控制JY 62022 数据采集卡完成。

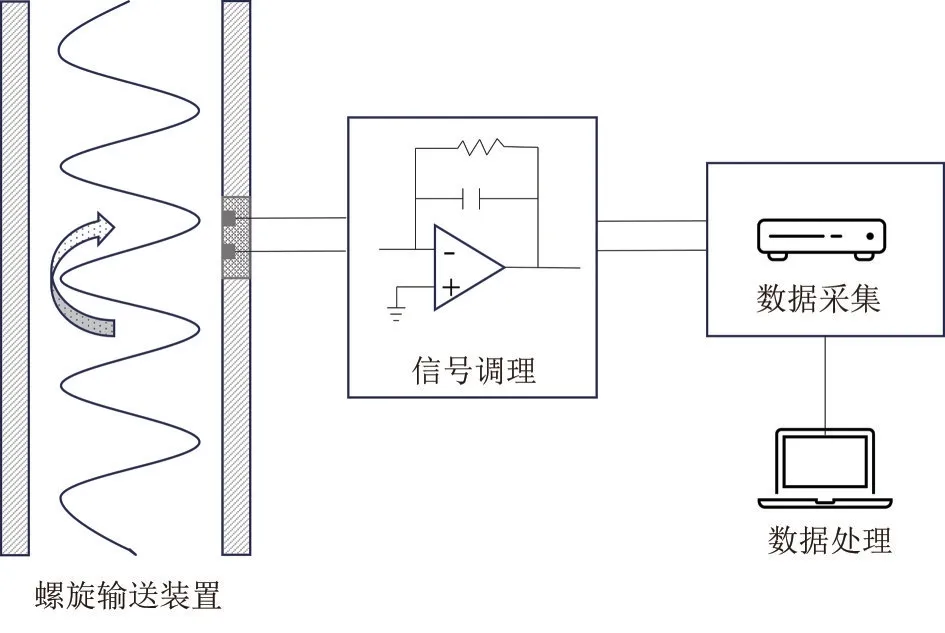
图3 静电检测系统

当带电颗粒经过传感器电极敏感区域时，由于静电感应现象，电极表面会产生感应电荷。由于信号调理单元采用了电流放大电路，因此获得的信号反映了感应电流的信息［式(1)］。

两个静电电极获得的感应电流信号，经信号调理单元并数据采集后，进行互相关计算。互相关函数计算的离散表达式见式(2)。

式中，N为用于进行互相关计算的点数；m为延迟的点数。

由Rxy峰值所对应的m值，可获得两个信号之间的延迟时间τ0。静电传感器电极间距已知，则可获得速度如式(3)。

式中，L为静电电极的间距。

1.2.2 螺旋叶片运动与速度检测的关系

建立螺旋输送的静态几何模型，依次将螺杆旋转不同的角度，观察螺旋叶片与电极的相对位置，如图4所示。

图4 螺旋叶片运动过程

在螺杆旋转的过程中，螺旋叶片沿螺旋的轴向方向做上升运动。在螺旋输送过程中，螺旋叶片会携带颗粒先后经过轴向排列的两个电极，因螺旋叶片是金属，电导率高，导电能力强，因此其对两个电极检测的静电信号影响很大，从而使螺旋叶片轴向上升过程反映在轴向电极检测的静电信号中，而且存在时间延迟。通过互相关函数计算时间延迟可以获得螺旋叶片的上升速度。

静电传感器检测到的为电极附近的局部颗粒运动产生的电荷信号，螺旋叶片与检测电极之间存在5mm 间隙，并且静电信号主要与螺旋叶片引起的颗粒的运动状态相关，因此金属材料制成的螺旋叶片以及颗粒的尺寸不影响对螺旋叶片运动速度的检测。

1.3 EMD分解

应用于螺旋输送机的静电传感器，采集到的信号中包括转移电荷信号以及电磁干扰噪声，直接进行相关测速计算，难以获得准确的延迟时间，因此采用EMD方法对信号进行处理。

EMD 方法适用于非线性和非平稳过程，由Huang等[9]提出。EMD分解后，信号x(t)可由线性方程式(4)表示。

式中，IMFi(t)为内禀模态函数；r(t)为信号x(t)的残余分量；n为内禀模态函数的个数。

将静电传感器采集到的两个电极的原始静电信号经过EMD 分解后，通过每一层的相关系数来选择信号进行滤波。

1.4 实验方案

实验中，输送的粉料采用1.5mm平均粒径的煤粉，设置6 种不同的螺旋输送机的转速，见表1。静电信号的采样频率为10kHz。

表1 实验条件

2 结果与讨论

2.1 原始静电信号分析

图5 为6 种不同转速时电极1 采集到的2s 原始静电信号。从图5中可以观察到，每个电极的信号具有周期性，并且这种周期性与螺旋的转速相关，随着螺旋转速的增加，相同时间内出现的周期性波形的个数也在增加。

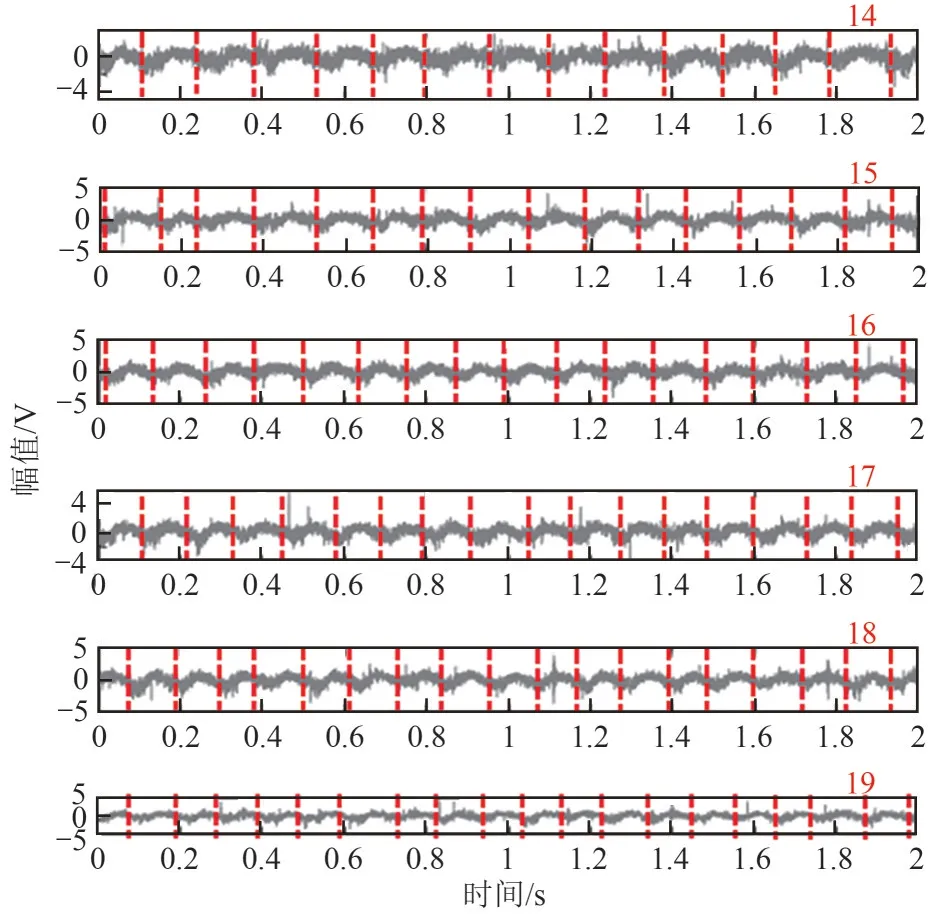
图5 原始静电信号

因为螺旋叶片为双螺旋结构，螺杆旋转一圈，螺旋叶片会经过电极两次，螺旋叶片每秒经过电极的次数与螺旋转速的关系如式(5)。

式中，k为螺旋叶片每秒经过电极的次数；n为螺旋转速，r/min。

采集到的信号中的周期个数与每种转速下螺旋叶片理论经过电极的次数关系见表2，两者具有很强的相关性。

表2 信号周期关系

转速为289r/min时，两个电极的原始静电信号如图6所示。从图中可以观察到两个电极之间的信号存在时间延迟，螺旋叶片在轴向上做上升运动，会先后经过管壁轴向方向的两个电极。因此两个电极之间的时间延迟代表螺旋叶片先后经过两个电极的时间差，通过该时间差可以计算螺旋叶片的上升速度。

图6 两个电极原始静电信号

2.2 基于EMD的静电信号滤波处理

转速为215r/min 时电极1采集到的原始静电信号经过EMD分解后得到的8个内禀模态函数如图7所示。每一个内禀模态函数具有不同的局部频率，图8 为每一个内禀模态函数对应的傅里叶频谱图，其中IMF1～IMF4 信号频率范围分布广，信号幅值小，IMF5 中主要频率为50Hz 的工频干扰，IMF6～IMF8 为集中在低频段的信号，信号频率范围小，但是信号的幅值大。

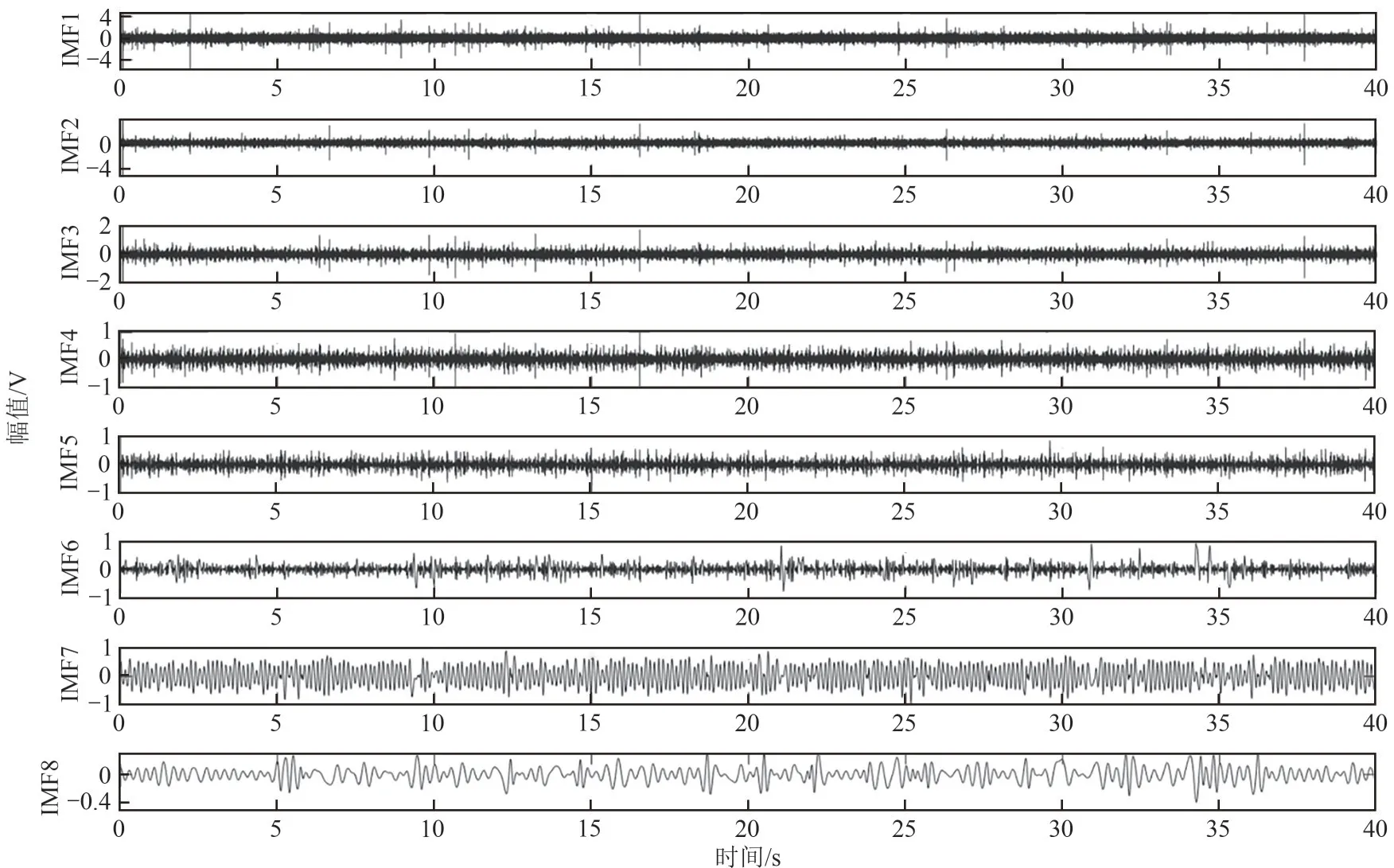
图7 EMD分解结果

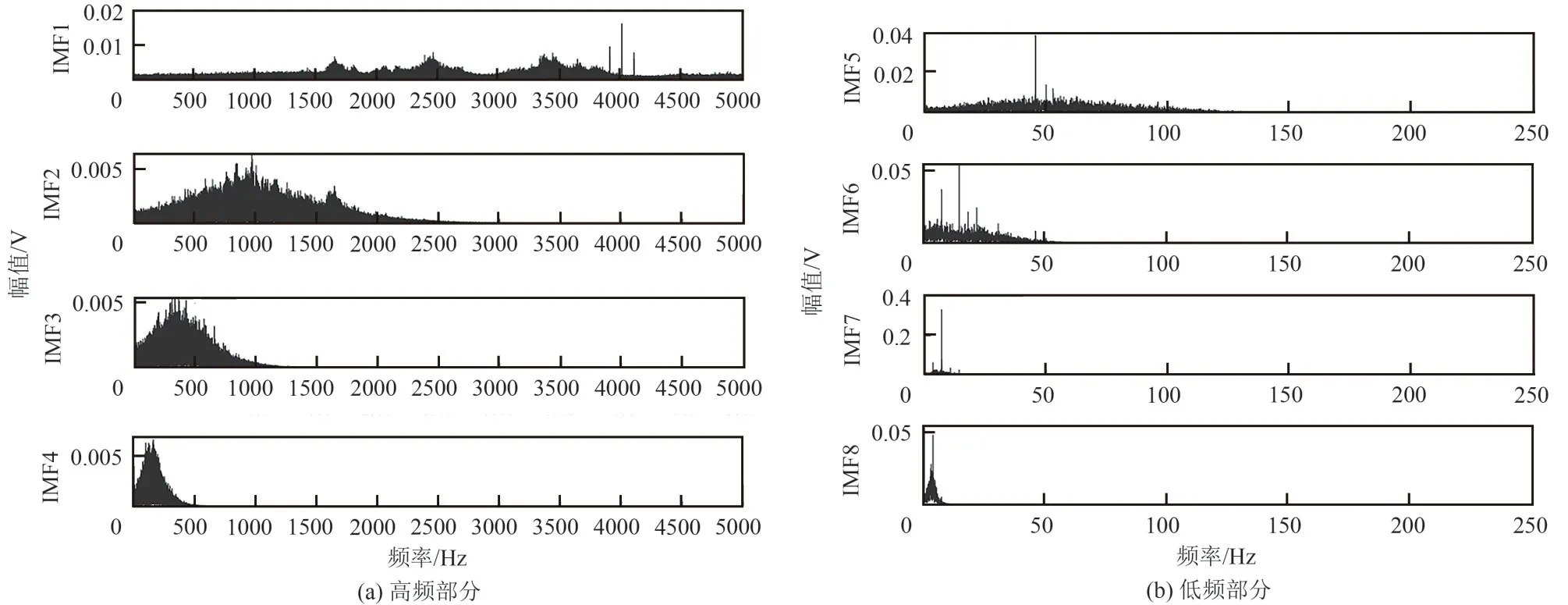
图8 IMF傅里叶频谱图

定义各内禀模态函数的能量分数如式(6)。

式中，Ei为内禀模态函数的能量，如式(7)。

每组转速不同的数据的两个电极的原始静电信号通过EMD 分解后得到的各个IMF 能量占比以及相关系数如图9所示，随着螺旋转速的增加，高频成分的内禀模态函数的占比逐渐减小，低频成分的内禀模态函数的占比逐渐增加。低频成分的内禀模态函数如IMF6～IMF8，其频率范围在0～50Hz以内，高频成分的内禀模态函数，如IMF1～IMF4，虽然幅值低，但频率在0～5000Hz 内都有分布，因此高频成分IMF1 的能量在静电信号中也占主要成分。随着螺旋转速的增加，占主要成分的低频成分从IMF7向包含更高频率的IMF6靠近。相关系数的大小与能量占比有相似的趋势，转速较慢时，低频部分的IMF7相关系数最高，随着转速的增加，IMF7的能量占比在减小，相关系数也在减小，IMF6 的能量占比在增加，相关系数也在增加。除了代表低频段的IMF6和IMF7的相关系数比较高，每组数据中的IMF1相关系数在0.4～0.5之间，因此分别对每组数据中的IMF1 进行高频段的分析，以及IMF6～IMF8相加的信号作为低频段的信号分析。

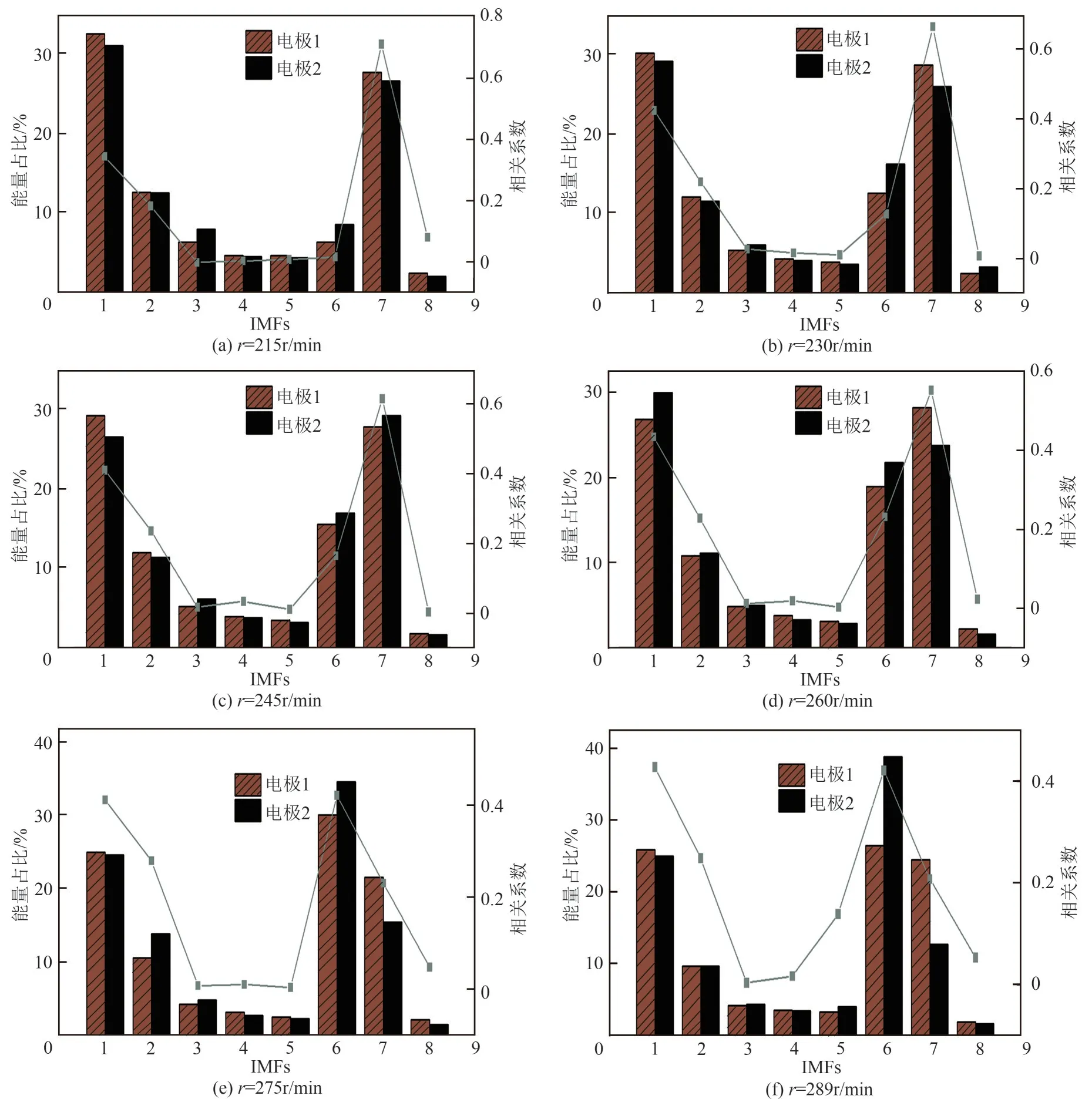
图9 IMF能量分数以及相关系数

从每组实验中的两个静电信号分解出的IMF1中选择2s 的数据进行互相关计算，互相关函数如图10所示。虽然IMF1的相关系数比较高，但是对应的延迟时间为0，因此EMD分解出的高频信号应该为螺旋输送带来的干扰，这种干扰在螺旋管道中的不同位置的电极处是相似的。

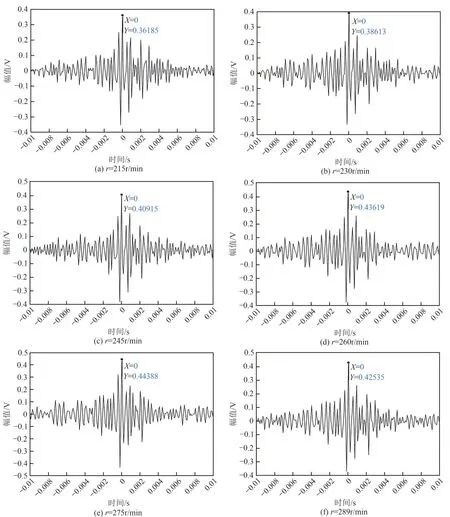
图10 IMF1互相关函数

将IMF6～IMF8 的信号相加选择为滤波后的低频信号，滤波后信号相关系数变化如图11 所示。滤波后相关系数得到明显提升，因此采用该信号进行螺旋叶片上升速度互相关计算。

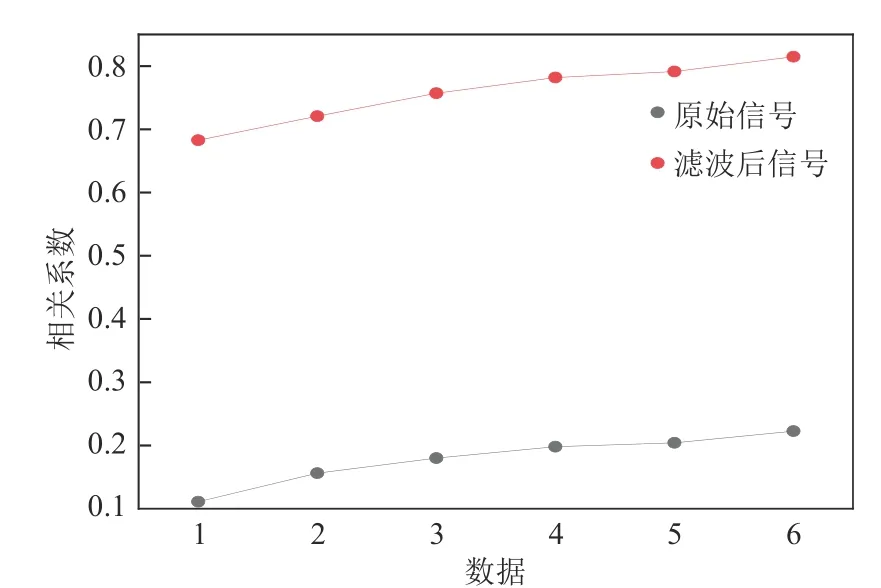
图11 相关系数

2.3 速度测量

为了评估测量系统的准确性，每组实验选择40s的数据，每2s的数据进行一次叶片上升速度的互相关计算，计算结果如图12 所示。其中，虚线为测量速度的平均值。

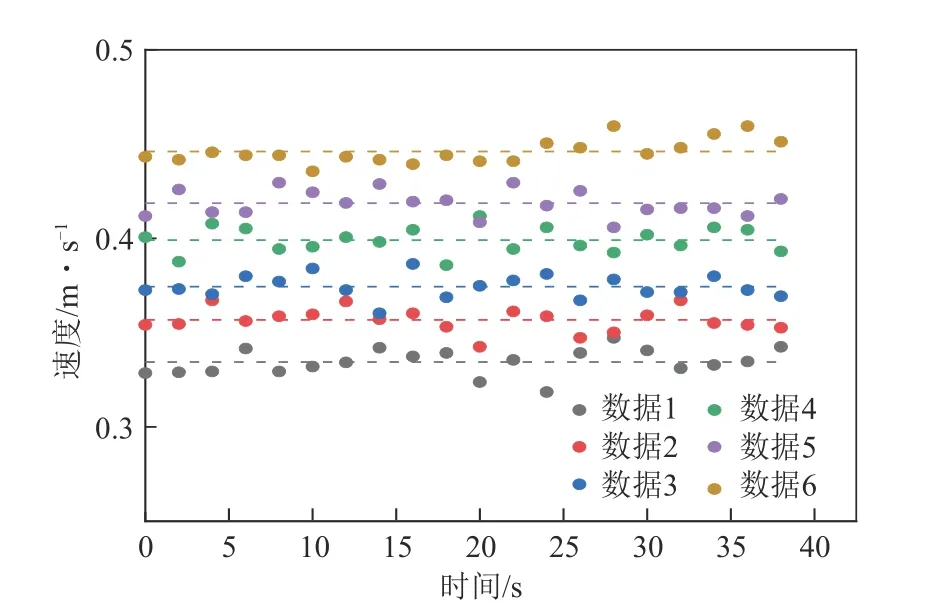
图12 静电检测的叶片上升速度

静电传感器测量的螺旋叶片上升速度通过式(8)转换为螺旋转速的测量值。

式中，v为螺旋上升速度；p为螺距。

采用数字转速表测量螺旋转速，测量精度为±0.05%。定义相对误差为式(9)。

式中，n为数字转速表测量的转速。测量结果如图13 所示。静电传感器测量的螺旋转速整体偏小，相对误差在 -3.9%至 -1.8%之间，平均相对误差为 -2.8%。主要原因在于实验中使用的螺旋叶片存在加工误差，导致螺距参数不准确，而且各段螺距也存在不一致现象，因此静电传感器测量的螺旋叶片上升速度也会产生波动。

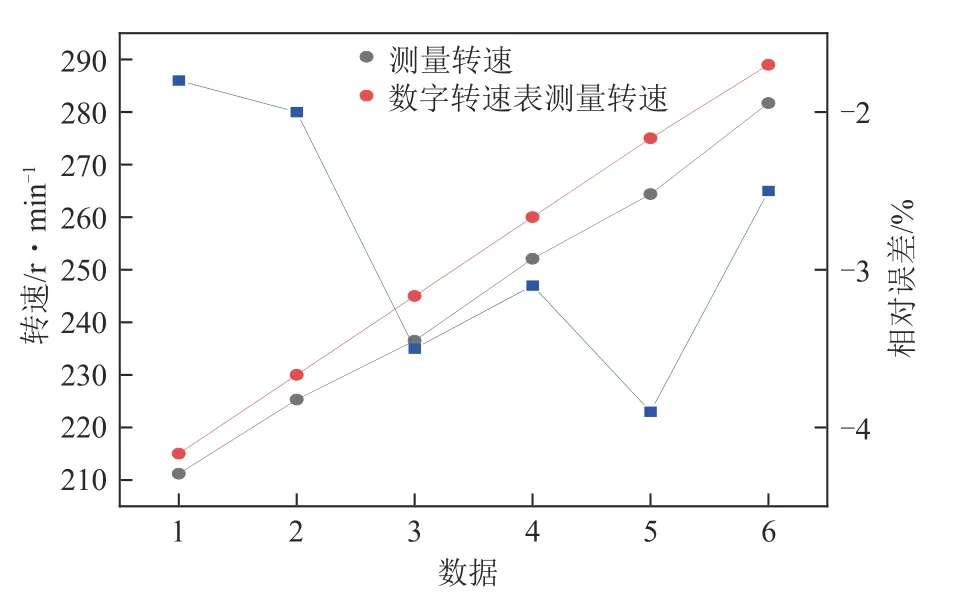
图13 螺旋测量转速与误差

为了修正静电传感器的螺旋转速测量结果，建立线性拟合修正式如式(10)。

式中，ng为修正转速。螺旋修正转速与相对误差如图14 所示，经过拟合修正后的螺旋转速平均相对误差为0.67%。

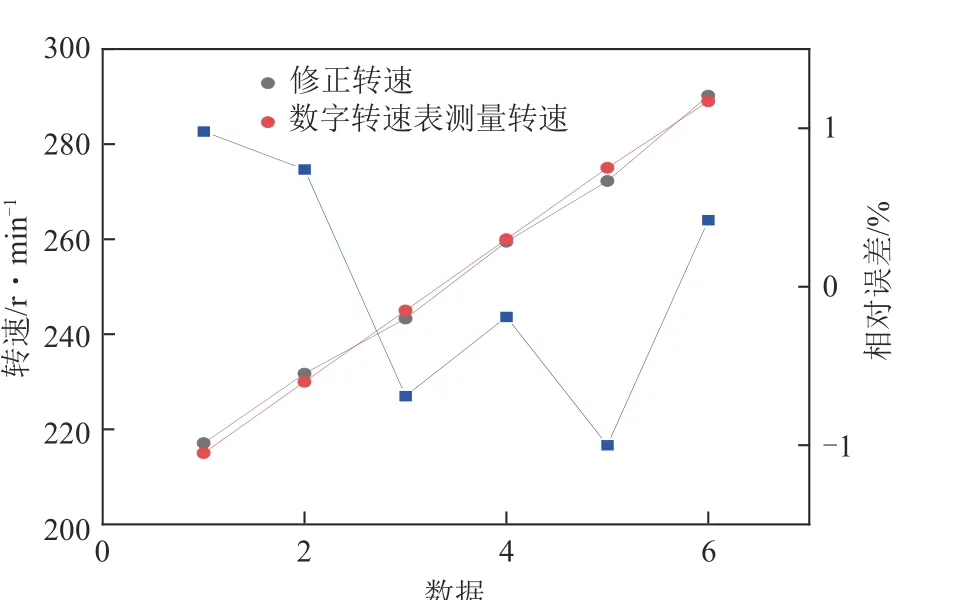
图14 螺旋修正转速与误差

3 结论

本文设计了用于检测螺旋输送机叶片运动状态的静电传感器，针对静电信号噪声干扰严重的问题，提出了基于EMD 的静电信号滤波处理方法。通过实验数据分析，得到如下结论。

（1）螺旋输送过程中，管壁处检测到的静电信号具有周期性，且与螺旋叶片经过电极的频次一致。

（2）利用基于EMD的静电信号滤波处理方法，可提高相关计算的相关系数。

（3）通过线性拟合修正螺旋加工误差对测量结果的影响，修正后的螺旋转速测量相对误差为0.67%。