超音速旋流分离器湿气出口段液膜测量

丁红兵，张盼盼，陈政奇，王世伟，梁真馨，孙宏军

（天津大学电气自动化与信息工程学院，天津 300072）

超音速旋流分离法是结合旋流分离技术和冷凝分离技术的多组分气体冷凝分离方法[1]，其发展非常迅速，最早可以追溯到1989 年利用旋风分离原理去除水分的“Condi-cyclone”空调冷却除湿技术[2]。2000年，Twister 设计出第一代超音速分离器Twister Mark Ⅰ[3]。2008 年，胜利油田与北京工业大学环境与能源工程学院联合开发了一款超音速分离器，并通过实验发现Laval 喷管的渐扩段在一定条件下将出现激波[4]。2018 年天津大学王孝通[5]设计了中心体式超音速分离器，并分析了超音速分离器核心部位结构对分离特性的影响情况。

作为一项新兴技术，目前对超音速分离器的研究集中于分离结构、凝结性能等方面，并未对超音速分离器壁面薄液膜的形成、演化及剥离规律有过多关注[6]。事实上超音速分离器实现气液分离的过程中，液体脱除过程规律至关重要，而液膜测量作为研究液体脱除规律的重要手段，具有很大的研究价值。天津大学孙宏军等[7]利用电导环装置制造了一种液膜测量传感器，测量了环形雾流下液膜厚度的变化规律。丁红兵等[8]则提出了一种改进的欧拉-拉格朗日-欧拉模型对超音速分离器内部流动机制进行了详细的分析。Jayakumar等[9]利用空气耦合超声技术来检测下降液膜的厚度，精度达到了3.48μm。王世伟等[10]建立了一种新型CFD模型并研究了入口压力对超音速分离器内流动特性的影响。Choi等[11-12]在柔性印刷电路板上安装电导传感器来测量液膜厚度，研究了不对称气流对液膜特性的影响以及横向气流对液膜流动的影响。Liu等[13]设计了八电极式电容层析成像装置，并利用迭代图像重建算法实现了微米级液膜的测量。张华承等[14-15]通过多种方法研究了不同气体密度和液相表面张力对液膜厚度的影响。曾杰等[16]利用超声多普勒测速仪和高速照相机研究了垂直平板和波纹板上液膜厚度分布。

本文开展超音速分离器的湿气出口段液膜测量研究，主要内容有：设计了一套微米级液膜标定装置，确保实验中液膜厚度测量准确；设计开发了一套基于FPGA激励和信号采集的FPC柔性液膜测量系统，可实现500μm 以下范围的液膜测量；搭建实验管段，研究了不同工况下超音速分离器的液膜特性，为进一步揭示超音速分离器气液流动规律提供了新的参考依据。

1 实验装置

1.1 超音速旋流分离装置

旋流前置式分离器如图1所示，其旋流发生在亚音速区，因此激波影响小，液滴二次挥发概率低，同时也能避免中心体等结构占据分离器有效流通面积，导致边界层效应增加[17]。分离过程中含湿气体以一定初速度进入分离器入口，超音速喷嘴段结构设计为先收缩后扩张，根据气体动力学的绝热膨胀流动规律[18]，气体通过喷嘴将加速、膨胀和降温，形成低温低压环境，有利于水蒸气发生凝结，随着含湿气流中水蒸气由未饱和转变为过饱和状态，小液滴凝结核形成并不断生长，同时由于气液混合物在旋流发生段做旋流运动，液滴所受离心力相比气相更大而被甩至壁面，实现气液分离，液滴撞击壁面后汇聚形成液膜与气流一起继续沿轴向流动，最终经气液分离段的排液间隙排出，较纯净的气体进入扩压器，因加速膨胀引起的气压和温度降低得以恢复。超音速分离器面积比为1.6，决定内部流动状态的三个特征压强比分别为0.9005、0.5967和0.1427[19]。

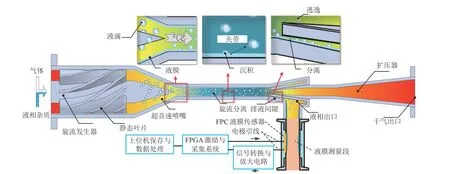
图1 超音速分离器分离与测量原理

超音速分离器的设计工况主要考虑了气体含液量与背压比的变化对分离性能的影响，其中背压比指的是外界反压与气体总压的比值，实验中通过电动阀控制分离器出口气压，以实现分离器不同背压的调节。实验中气体含液量的变化范围为0.85～11.66L/h，背压比的变化范围为0.35～0.717。实验结果表明，当背压比从小增大到第二特征压强比附近时会产生激波，严重破坏气液旋流分离过程，使得液膜破碎并夹带出液滴，气液混合物同时经干气、湿气出口排出，使得湿气出口处液膜厚度显著降低。

1.2 实验管路

气相实验管路如图2(a)所示，空气压缩机提供压缩气源，经冷干机和过滤器去除杂质后储存；自力式调压阀保证缓冲管内气源稳定；电动阀1开度控制实验管路气压；蒸发罐用来改变气体湿度；电动阀2 控制分离器出口气压，实现不同背压的调节；实验废气通过消音器后排出。气相实验管路设置若干监测点，其中P1检测气源气压，确保气源安全，T1、P2检测加热器出口气体参数，Tin、Pin检测分离器入口气体工况，Pout为检测分离器出口气压。

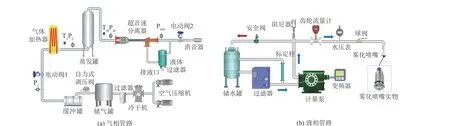
图2 实验管路

水路喷雾实验系统如图2(b)所示，通过雾化喷嘴注入微小液滴的方式控制气体含液量。雾化喷嘴内部有不锈钢导流叶片，液体高速流动并在导流叶片的作用下形成离心旋涡，最终以射流形式由孔口喷出，形成空心锥喷雾。除雾化喷嘴外，水路喷雾实验系统还由储水罐、过滤器、标定柱、计量泵、变频器、脉动阻尼器、齿轮流量计和水压表等组成。实验用水先经过滤器过滤，后被隔膜式计量泵周期性定量输送至实验管路，变频器控制水路流量与水路压力，阻尼器抑制水路压力脉动，齿轮式流量计和水压表实时检测水路参数，并同时将检测结果远传至MCGS上位机显示并保存，标定柱配合高精度秒表可以对水路实际流量进行标定，为确保流量准确，需定期标定水路流量。部分实物如图3所示。

图3 部分实物

1.3 FPC柔性液膜传感器

超音速旋流分离器的入口，出口及湿气出口均以管道方式连接，在流体流动的内壁面不存在较为平整的区域，导致体积大且无法弯曲的传统硬质电路板的应用受到限制，故基于FPC技术设计加工一款液膜测量传感器。如图4(a)、(b)所示，柔性材料选用150mm 的聚酰亚胺（PI）作为基材，电极、焊盘及导线选用延压铜制作，铜箔层厚度设计为35μm（1OZ），线宽0.2mm，利用沉金工艺在电极表面覆盖0.025μm的金层保护，防止氧化电解和保持良好的导电性，最终实物如图4(c)所示。实验电极形状选择圆形以避免尖角对各向异性电流分布的影响，同时也易于加工和保证精度。收发电极与接地电极间隔排列可以减小电极对间串扰，以及最小化空间假频（spatial aliasing）效应。实验中的测量区是以所选取电极对为对角的矩形区域。测得的信号与传感器本身设计和布置形式有关，但是无论是在标定实验还是不同工况下进行的测量实验中，均使用同一传感器并且在管壁采用平齐安装，因此可以忽略传感器布置对信号的影响。

图4 FPC柔性电路板设计

电极半径是影响传感器输出特性的主要因素之一，为此重点研究了电极半径r为0.2mm、0.25mm、0.3mm和0.4mm时的电流输出特性，为确保传感器在测量范围内的响应灵敏度和线性度，参考电极在实物制作时的最小引线宽度，电极半径最终选择r=0.25mm。同样为了最优化传感器的可测范围和响应特性，最终确定电极阵列的间隔d=1mm。接着研究了接地电极的半径R分别为0.25mm、0.35mm 和0.45mm时不同液膜厚度下的接收电极输出电流值。考虑到在不改变电极分布规律的基础上，适当增大接地电极不仅有助于输出信号的检测，还可降低电极对间串扰，本文的接地电极半径确定为R=0.45mm。

1.4 液膜标定装置

设计加工的FPC柔性液膜传感器需要进行标定实验，以确保液膜厚度测量准确。为实现微米级移动的标定功能，设计开发了一套静态平面液膜标定装置，如图5所示，大致由五部分组成，分别为上盖、立柱、底座、微米移动尺和移动平面。整体为长250mm、宽200mm、高150mm 长方体，材质为绝缘材料有机玻璃，上盖、立柱和底座以通孔直插式进行连接，末端利用螺母紧固。微米移动尺选用带数字显示的螺旋测微头，分辨率为1μm，测量精度能够达到4μm。测微头端面穿过钢制弹簧夹，两者包含于特殊设计的移动平面尾部，经弹簧夹专用螺母夹紧。

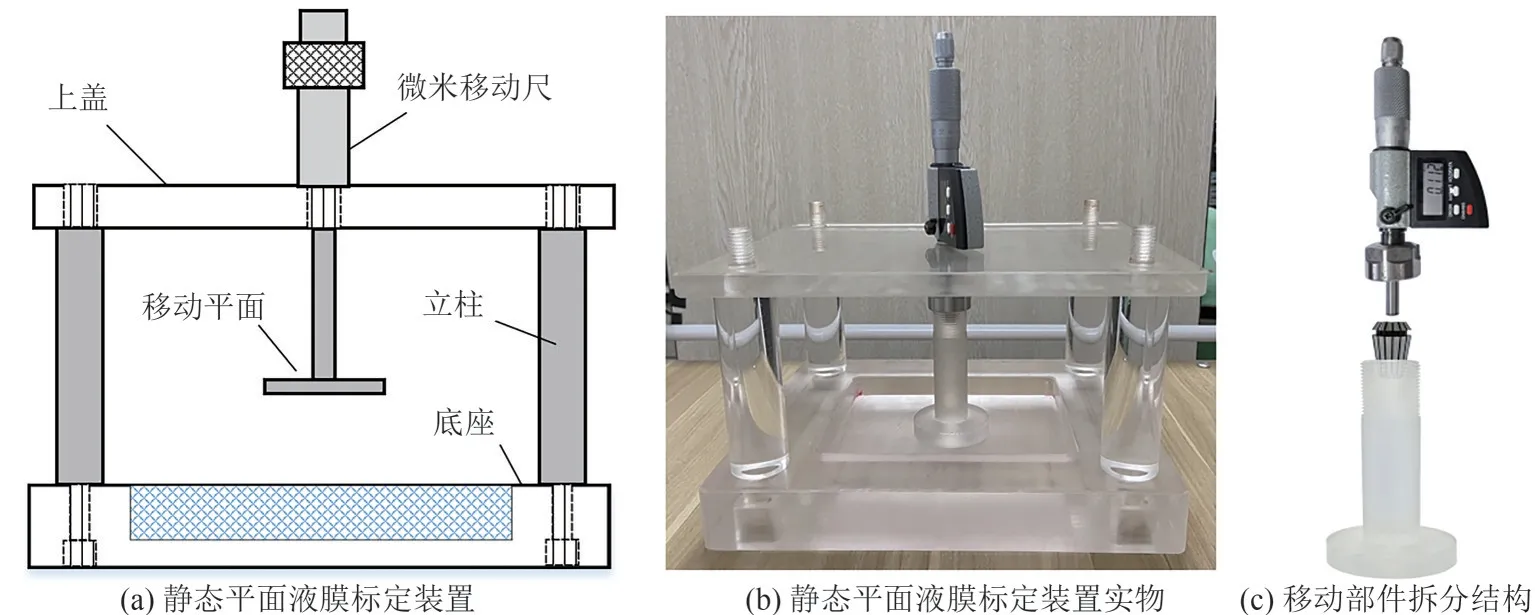
图5 静态平面液膜标定装置

进行标定实验时，首先将传感器固定在标定装置水槽底部中央，通过微米移动尺将移动平面下降紧压传感器，将微米移动尺示数置0，随后微调微米移动尺使平面上移，每次移动距离为50μm，每次移动等到稳定后再采集电极输出信号，重复上述操作完成电极在覆盖0～1000μm范围内的液膜响应数据。考虑到不同电极存在的微小差异和电极排列位置的不同等因素的影响，以及为了方便不同位置测得的信号进行比较，本文对电压信号进行了量纲为1化处理。

1.5 基于FPGA的液膜测量系统

FPGA 开发板提供50MHz 的内部时钟，利用PLLIP 核对该时钟进行倍频或分频，以满足不同的时钟频率需求。设置FPGA 的DDSIP 内核模块参数即可生成所需频率的正弦激励，再经高速DA转换器得到相应的阶梯状模拟电压信号，经低通滤波得到最终的平滑连续波形。实验使用AN108模块实现AD 和DA 转换功能，最终使FPGA 输出稳定的1kHz、幅值2V 的正弦激励信号。FPGA 与AN108 模块实物如图6 所示。液膜使电极导通时产生的电流非常微弱，必须经过放大才能被采集并处理分析。所需放大的电流频率为1kHz，放大倍数需要在10000 倍以上，实验选用AD8066 运算器实现电流转电压并放大功能。采用两级放大方式，第一级为电流转电压并进行1000 倍放大，第二级为1000 倍可调电压放大，放大电路原理和实物如图6 所示。实验中使用FPGA 自带的滤波电路实现噪声抑制。为了保持液膜厚度与输出电流之间的线性关系，交流激励下应尽量降低电极对间的容抗效应影响，实验选取激励频率为100kHz，因而根据香农采样定理，为了保证采集得到的信号不失真，采样频率设置为200kHz。

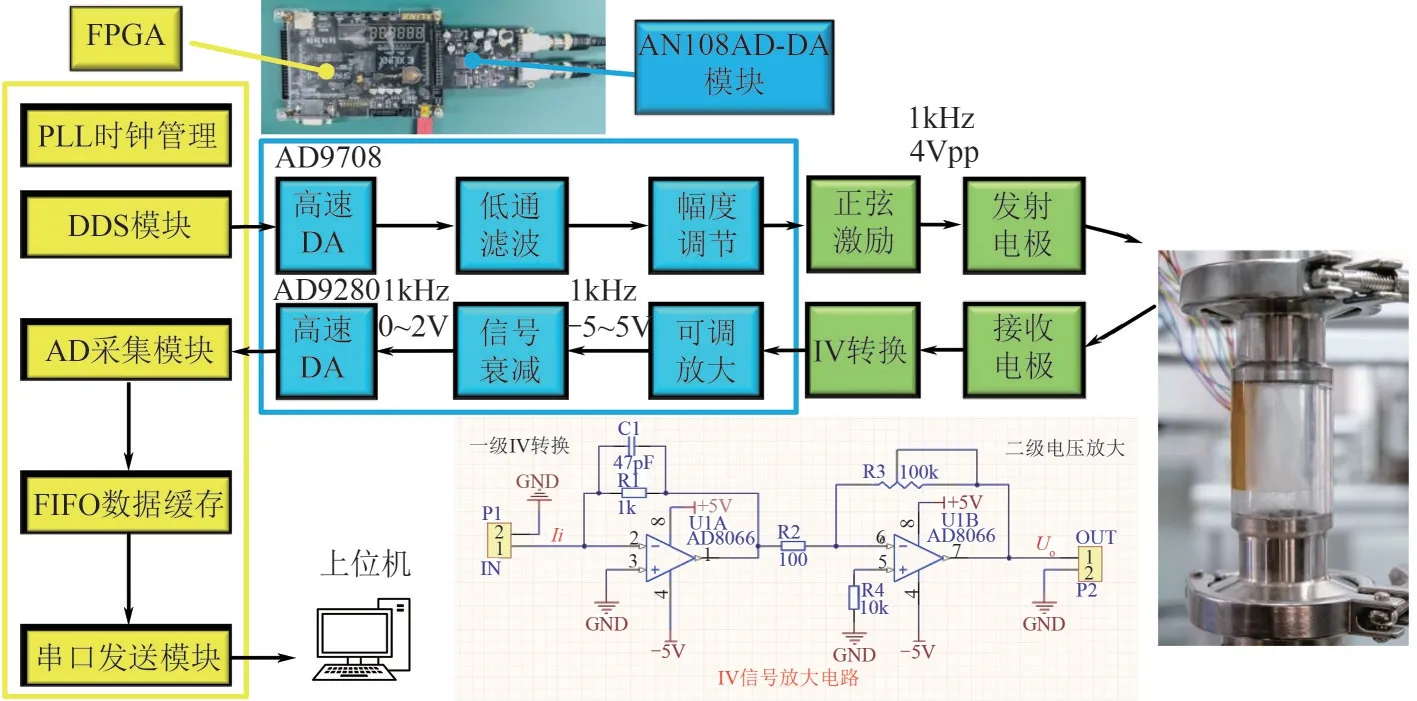
图6 基于FPGA的液膜测量系统

2 结果与分析

2.1 液膜标定结果

使用平面液膜标定装置与FPGA 激励采集系统，对FPC柔性液膜传感器上的电极开展平面液膜标定实验。采用包络解调方法从输出电压信号中提取电压幅值，并对电压幅值V进行量纲为1 化处理，得到结果如式(1)所示。

式中，Vmax为饱和液膜厚度下的电压幅值；Vmin为无液膜时的电压幅值。因此特性曲线中的量纲为1 化电压V*均在0～1 范围内。标定过程以1 号电极为激励，2号电极接收为例。

由图7可以看出，液膜传感器在500μm以下范围灵敏性较高，而超过500μm后基本达到饱和，失去对液膜厚度的分辨率。采用有理多项式模型[20-21]对量纲为1电压V*和液膜厚度h之间的关系进行拟合求取，拟合结果如图7所示，拟合关系如式(2)所示。

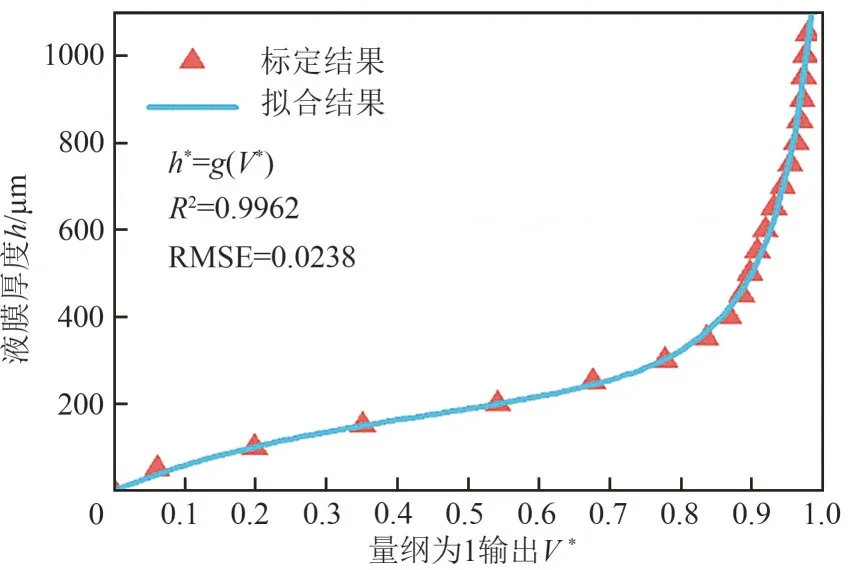
图7 标定数据与拟合结果对比

式中，h*为拟合计算所得的液膜厚度。由于实际测得液膜厚度较薄，大致范围是50～200μm，为了提高薄液膜的测量灵敏度和精度，将设计传感器的测量范围确定为50～500μm。当液膜厚度超过500μm 后，信号的敏感度降低，噪声影响会增大，本液膜传感器不再使用。图8展示了标定数据与拟合结果的误差范围，可以看出在测量区间内，关系式(2)对液膜厚度的拟合误差始终在±5%范围内，精度较高，可完成液膜传感器量纲为1输出电压对应的液膜厚度之间的换算。

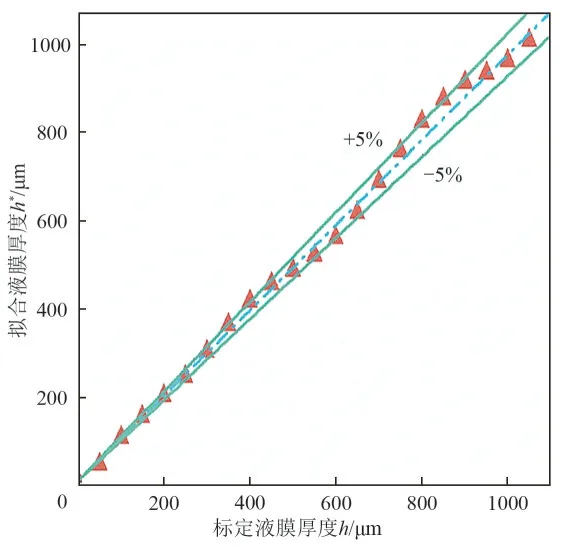
图8 拟合结果误差线

2.2 不同工况对液膜影响的时域分析

实验采集了不同入口含液量和背压比下，以1 号电极为激励，2 号电极接收的电压信号。电压信号经解调和换算后得到液膜厚度h，部分结果如图9所示。以左上和右下两种情况为例，其出现随时间极不规律变化是液滴随机流动特有的规律。当流形为液滴随机流动，液滴未达到传感器测量区时，测得液膜信号极小，近乎为0，当液滴达到传感器测量区时，测量信号会剧增，液滴随机进入传感器测量区使得信号随时间极不规律变化。由于实验使用同一传感器并且在管壁采用平齐安装，每组电极的尺寸与参数相同，理论上采用其他电极对进行的实验数据分析也是类似特征，后续实验表明不同电极对得到的信号确实具有极高的相似性。

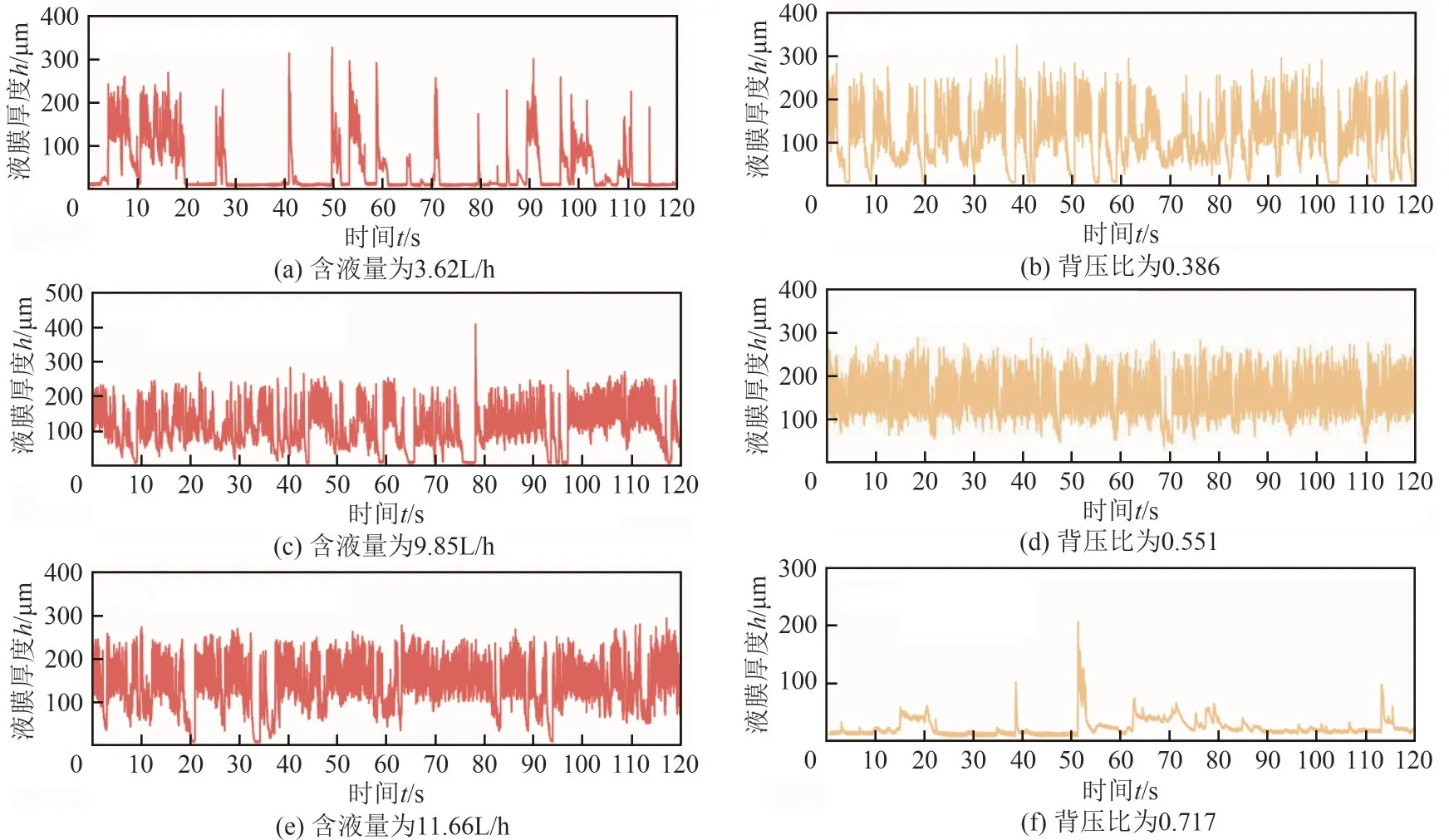
图9 不同条件下液膜厚度h随时间t变化曲线

对特征较为明显的工况下液膜厚度数据进行分析，部分统计结果如图10 所示。液膜厚度的分布存在明显的双峰特性，且随入口含液量的增大，分布整体向液膜变厚的方向移动，双峰从左高右低逐渐过渡到左低右高，表明液膜变厚的趋势突出。采用两项高斯分布进行拟合如图10 所示，代表较薄液膜厚度的峰位置特征μ1随含液量的增加增幅缓慢，在一定程度上代表了液体浸润壁面形成的稳定基层液膜，而代表较厚液膜的峰位置特征μ2随含液量的增加增幅较为明显，能够表征入口含液量变化引起的液膜厚度增加。

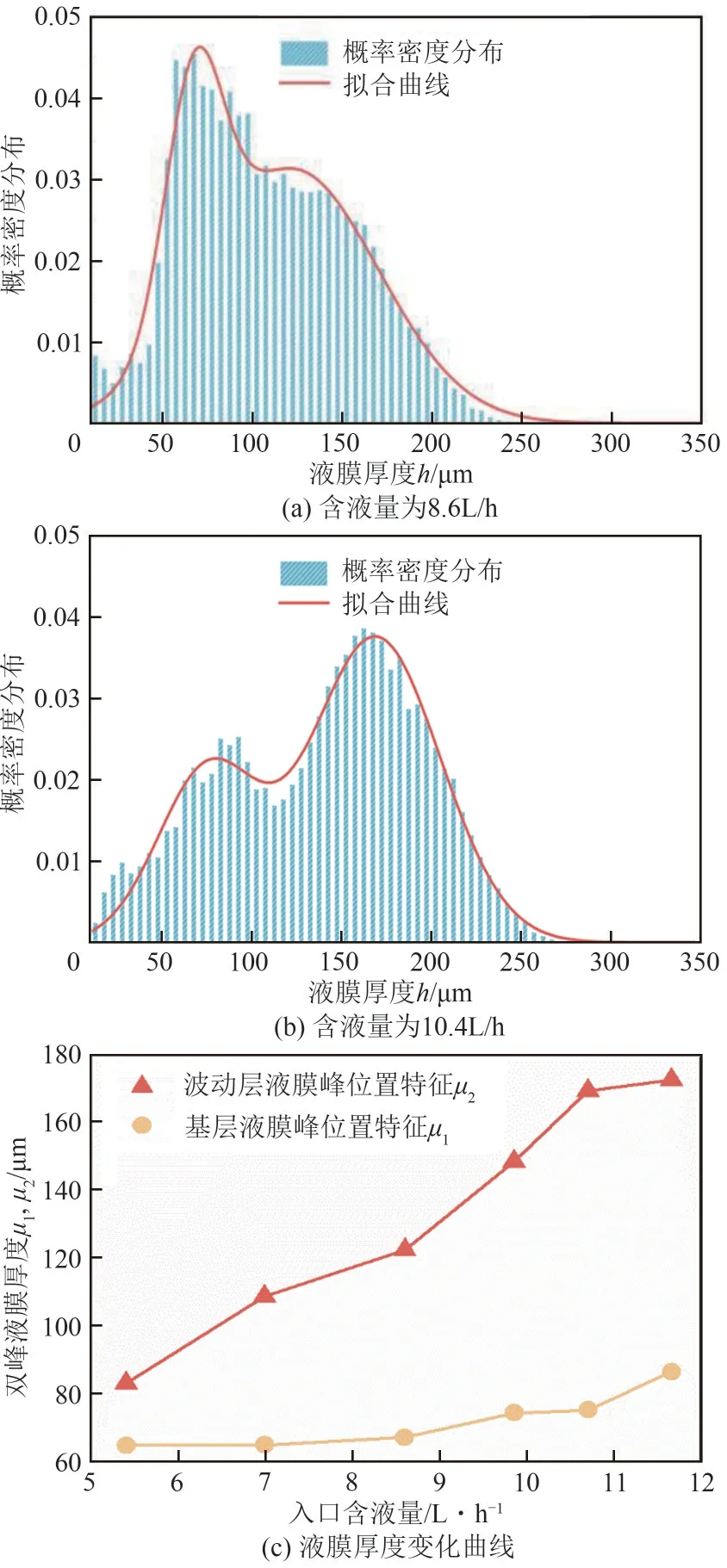
图10 不同入口含液量下液膜厚度h的概率密度分布及拟合曲线与峰值液膜平均厚度随入口含液量变化曲线

图11 为不同背压比下液膜厚度数据部分处理结果，在背压比较小时液膜信号呈现双峰分布，当背压比逐渐增大，双峰逐渐演化为单峰分布。由于湿气出口流动复杂，气相速度较快容易对液膜产生扰动，使分布出现双峰特点，随着背压比增大，当到达第二特征压强比临界值时，分离器前后压差减小，气相速度降低，气相剪切和间歇扰动作用减弱，使液膜能够保持一定厚度持续流动，分布逐渐演化为单峰正态分布，平均液膜厚度约155μm。背压比继续增大至第二特征压强比附近时，激波的形成使得气液分离遭到破坏，大量未被充分分离的液滴随气相排出，湿气出口液膜厚度显著降低，使得分布以较大比例集中在低液膜区间，μ1、μ2均表现为先增加后减少的规律，由于在第二特征压强比附近增减性发生转折，验证了激波对气液分离性能造成的不利影响。

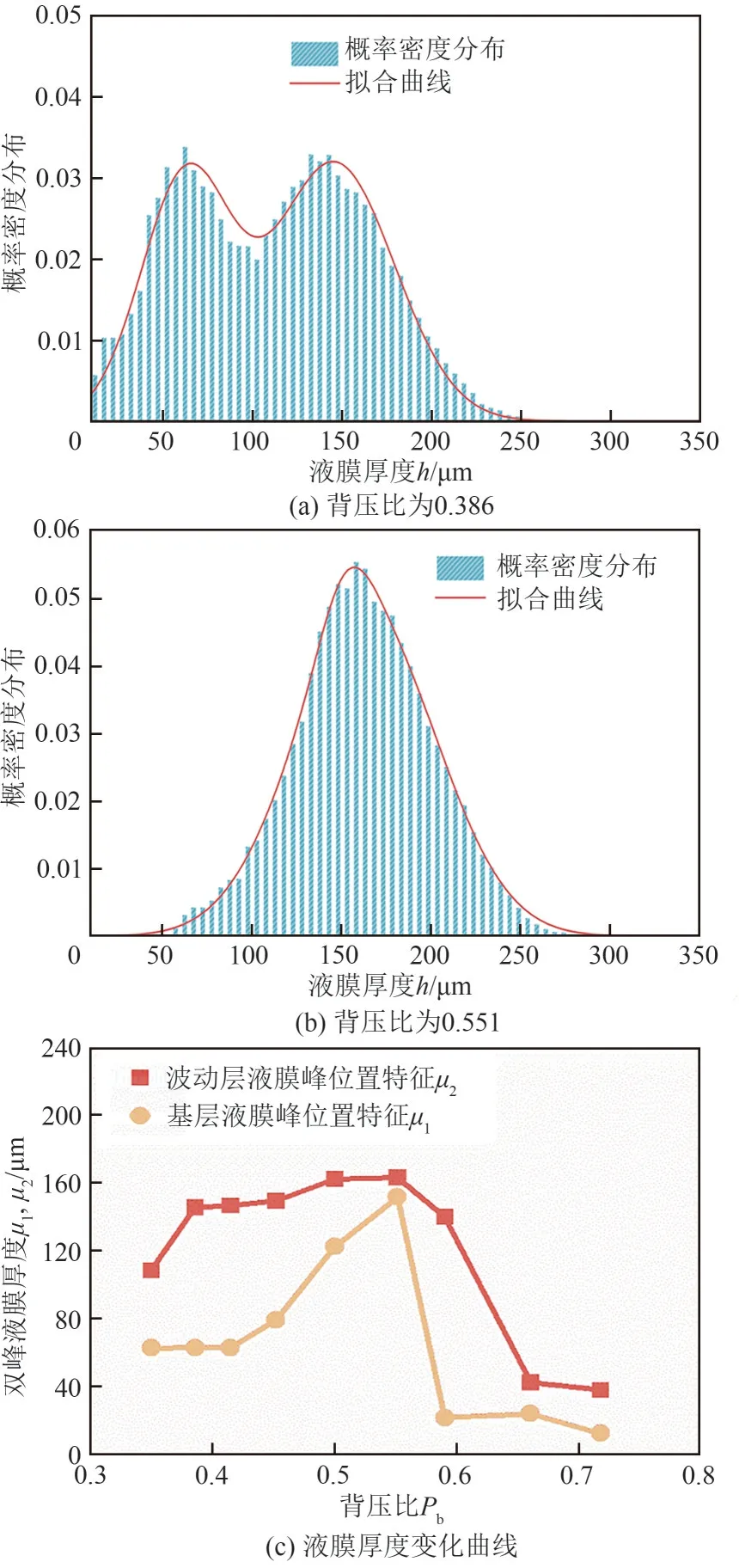
图11 不同背压比液膜厚度h的概率密度分布及拟合曲线与峰值液膜平均厚度随入口含液量变化曲线

2.3 不同工况对液膜影响的频域分析

为了研究液膜信号在局部时间内的非平稳特性，先后采用小波包分解重构和局部均值分解（LMD）方法对液膜厚度的时间序列进行处理，并对处理结果提取近似熵绘制特征图，分析液膜流动特性，最后使用K-means算法对特征聚类分析。

小波包分解可以同时对高频和低频区域进行既无冗余也无疏漏的分解，能够对包含大量中、高频信息的信号进行更好的时频分析[22-23]。其分解计算公式与重构计算公式分别如式(3)、式(4)所示[24]。

利用db4小波函数对液膜信号进行4层小波包分解，由于第1频段代表原始信号的低频趋势性，其变化幅度大且能量占比高，会降低对其他频段分析的准确性，因此不考虑第1频段。计算其他频段的归一化能量占比，第11～16频段归一化能量占比均较小，绘图时仅展示第2～10频段归一化能量占比。

由图12(a)可知，随着入口含液量从0.85L/h 增加到11.66L/h，第2和第3频段的归一化能量占比均会减小，其分别下降约0.160和0.103，其他频段的归一化能量占比均有增长，说明能量分布会由低频段向高频段移动。如图12(b)所示，随着背压比从0.35增加到0.717，在激波形成前第2和第3频段的归一化能量占比也会下降，最多分别下降约0.106和0.031，其他频段的归一化能量占比均有增长，随着背压比继续增大，激波的形成会使能量分布移动方向改变，第2和第3频段的归一化能量占比显著增加，到背压比为0.717 时分别增加约0.168 和0.148，其他频段的归一化能量占比则均有下降。综上，液膜的低频波动主要集中在第2 和第3 频段，高频波动主要集中在第4～16频段，因此将第2～3频段组成新的低频部分，第4～16频段组成高频部分进行小波包分解重构。图13 展示了含液量为9.85L/h与背压比为0.386 时的液膜原始信号处理结果，其中由上到下第一幅图为原始液膜信号，第二幅图为重构后低频分量，第三幅图为重构后高频分量。

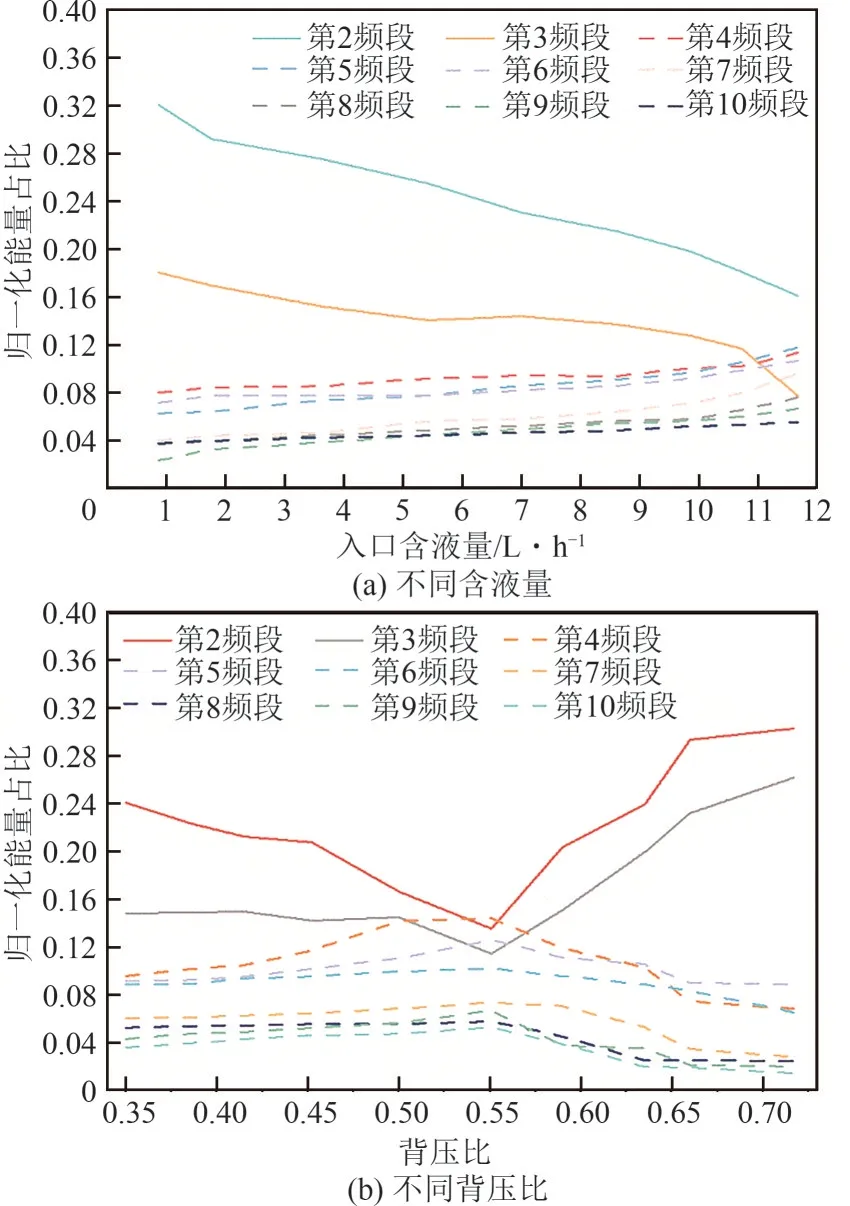
图12 不同工作条件下液膜信号不同频段的归一化能量占比变化曲线

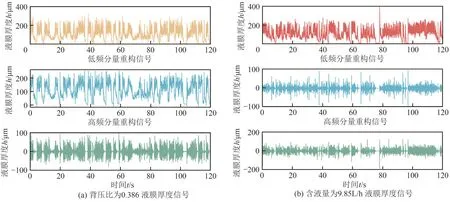
图13 小波包分解重构部分结果

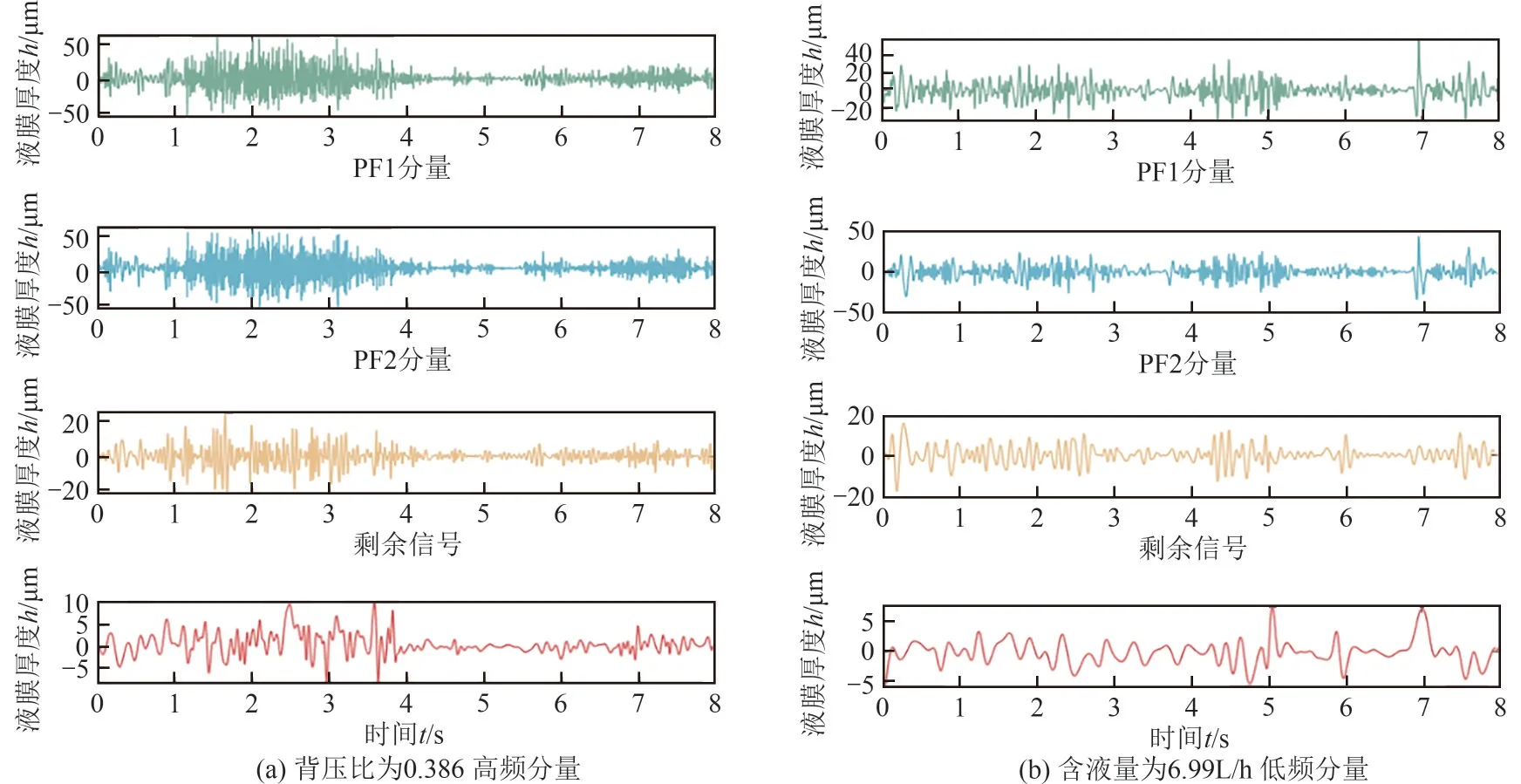
图14 局部均值分解部分处理结果

局部均值分解能够根据信号自身特点将复杂的多分量调幅调频信号分解为有限个单分量调幅调频信号之和，进而对瞬时频率和幅值进行组合，得到原始信号完整的时频分布。对于任意确定的信号x(t)，LMD算法的具体流程[26-27]如下。

（2）从原始信号x(t)中将局部均值函数m11(t)分离出来，得到h11(t)=x(t)-m11(t)。

（4）模态分量的包络信号是迭代过程中所有局域包络函数的乘积：a1(t)=a11(t)a12(t)…a1n(t)=∏nq=1a1q(t)。模态分量a1(t)为包络信号a1(t)与纯调频信号s1n(t)的乘积，即a1(t)=a1(t)s1n(t)。

（5）从原始信号x(t)中将a1(t)分离出，得到剩余信号u1(t)，重复以上过程k次，直到uk(t)为单调函数，如式(6)所示。

实际应用中数据长度N一般为有限值，按照上述步骤得到的是序列近似熵的估计值记为式(8)。

实验取N=2000，m=2，r取0.2倍的序列标准差，求取不同工况下最终分解得到的PF分量的近似熵，将其作为特征值绘制为特征图如图15所示。

图15 不同工作条件下各频率分量的近似熵变化规律图

随着超音速分离器入口含液量的增加，高低频信号PF 分量的特征值总体上都呈现出上升趋势。当含液量从较小值增大时，湿气出口段逐渐形成液膜流动，液膜厚度信号变大，高低频分量信号增大，波动程度也均有增大，故特征值均有增长；在液膜形成后逐渐增大含液量，液膜厚度稳定增加，低频信号波动程度保持一定程度上的稳定，故特征值增长不明显，而随着液膜厚度增加，液滴飞溅和融入的概率变大，高频信号波动程度会增大，故特征值稳定增长。

随着背压比的增加，特征值的变化较为复杂。当背压比小于0.551时，分离器工作在超临界流动状态，管道内无激波，随着背压比接近第二特征压强比临界值，激波的形成影响气液旋流分离性能，高低频信号波动程度都会增大，特征值均有一定的增长；当背压比大于0.551时，激波会严重降低液旋流分离性能，使得湿气出口处液膜厚度显著降低，液膜厚度信号显著减小，因此高低频分量信号显著减小，波动程度迅速减小，特征值均大幅下降，随着背压比继续增大，湿气出口段不再能形成稳定的液膜，而会出现随机分布的液滴流动，导致高频信号出现剧烈的波动，对应特征值又会迅速上升。

K-means聚类是当前应用最广泛的聚类算法之一，其主要流程[29-30]如下：随机选取K个数据点作为初始中心C，计算每个数据点到各个中心cj的欧式距离，将其归类到最近的中心cj对应的簇Aj；将簇内平均值作为新的聚类中心点，判断前后两次迭代得到的聚类中心点变化量是否小于预定值，是则输出聚类结果，否则重复上述步骤。

采用K-means算法将特征值聚为三类，如图16所示。此处的聚类结果与本研究的实验数据分析结果高度相似，流形的变化导致液膜厚度信号的特征发生了显著的改变，聚类算法根据特征的不同将液膜信号分为三类，又对应了不同的流形。当入口含液量较小时，液膜尚未形成，流形为液滴随机流动，传感器测得信号小波动弱，近似熵值小；逐渐增大入口含液量，流形变为丝状螺旋流动，液膜已形成且波动程度增强，近似熵值有所增大；继续增大入口含液量，流形变为环雾状流动，液膜厚度增大，液膜波动更加剧烈，近似熵值有一定幅度的增加。

图16 不同入口含液量下聚类结果

2.4 不同工况对液膜扰动波速度特性影响的分析

为了研究液膜扰动波的速度特性，建立一套互相关测速系统如图17 所示，当发射电极T1和T2横向排列，纵向的电极R1和R2将采集液膜扰动波速度的流向分量信号，当T1和T2纵向排列，横向的电极R1和R2将采集液膜扰动波速度的周向分量信号，通过此原理，可以测量湿气出口段不同方向的扰动波速度。

图17 互相关测速系统

通过互相关算法处理湿气出口段的液膜厚度波动信号可得两接收电极表面液膜波动的延迟时间[31]。用两个电极之间的距离d除以延迟时间τ0可以计算出扰动波的互相关速度。已知上游传感器信号y(t)和下游传感器信号x(t)之间存在时间延迟，互相关算法[32]如式(9)所示。

式中，S为样本个数；T为内相关段的长度；Δ为两个相关点之间的时间间隔；i为互相关计算中的数据点标签；j为互相关函数的峰值。时间延迟τ0=jΔ。液膜扰动波速度Vτ=d/τ0。

以气体含液量为8.6L/h 条件下求液膜扰动波速度的周向分量为例，由图18 可以看出互相关时间延迟τf为25.8ms，已知两接收电极间距为2mm，扰动波速度的周向分量计算为77.5mm/s。计算不同进口液流量下的扰动波速度，每一条件下的数据分为10 组可得10 组互相关速度，将平均扰动波速度视为实际液膜扰动波速度，用均方根误差（RMSE）描述波动率，结果如图19 所示。从结果可以看出，随着进口液体流量的增大，液膜扰动波速度指数增长趋势。扰动波速度流向分量的RMSE 在气体含液量小于8.6L/h 保持相对稳定，继续增大进口液体流量，其数值会有显著提升，实验过程中其数值范围为1.15～4.51mm/s；扰动波速度周向分量的RMSE 在气体含液量小于10.7L/h保持相对稳定，继续增大进口液体流量，其数值才开始上升，并且仍然小于扰动波速度流向分量的RMSE，实验过程中其数值范围为1.20～3.38mm/s。

图18 周向速度的计算过程

图19 流动方向和周向互相关速度的平均计算值和RMSE

3 结论

开发了一套基于FPGA 激励和信号采集的FPC电导式液膜厚度测量系统并进行了标定实验确保测量准确度。在不同的工作条件下进行了测量实验，获取了液膜信号，通过一系列的数据处理方法分析了液膜厚度分布与变化规律以及液膜扰动波速度的变化规律，得到结论如下。

（1）通过标定实验验证了FPC 传感器的精度，拟合误差小于5%；通过统计学分析可知超声速分离器湿气出口段液膜厚度在常规工作条件下呈双峰分布，基层厚度约为70μm，其波动厚度随工况变化而变化。激波的出现会严重影响液膜的形成。

（2）通过小波包分解后求取各频段归一化能量占比可知，随着入口含液量和背压比的增大，能量分布向高频段移动，液膜波动剧烈，有激波和没有激波的能量分布移动方向相反。入口含液量增加，第2和第3频段的归一化能量占比分别下降约0.160和0.103。第2、第3频段与其他频段能量分布变化趋势有明显差异，据此将第2～3频段重组为低频部分，第4～16频段重组为高频部分。

（3）对重组信号重构、局部均值分解与近似熵特征值提取可知，随着气体含液量的增加，液膜信号波动会逐渐剧烈，随着背压比的增大，液膜信号的低频分量波动程度会先增后减，在激波形成的临界值附近到达峰值，高频分量在背压比较低时波动趋势与低频分量相似，在背压比继续增大后由于流形变为了液滴随机流动而波动程度剧烈；最后采用K-means算法将提取的特征值聚类为三类，分别对应液滴随机流动、丝状螺旋流动和环雾状流动三种流动形式。

（4）采用互相关算法对湿气出口段不同流向的液膜扰动波速度进行了测量。结果表明随着入口含液量的增大，扰动波速度流向与周向分量均呈指数增长趋势，其中流向分量范围为84.7～339.0mm/s，周向分量范围为54.8～186.4mm/s，扰动波速度流向与周向分量的RMSE都保持相对稳定，直到相应临界值后有较大幅度的增加，并且扰动波速度的流向分量和增加比大于周向分量和增加比，流向分量的RMSE 数值范围为1.15～4.51mm/s，周向分量的RMSE范围为1.20～3.38mm/s。