阻力相关参数对比分析研究
李天瑜,陈定君,张明远
(1.陕西理工大学 机械工程学院,陕西 汉中;2.重庆公共运输职业学院,重庆;3.陕西交控集团西略分公司,陕西 汉中)
引言
液压挖掘机在现代建筑和土木工程中非常重要。它们被广泛用于挖掘、开挖、搬运、平地和其他各种建筑活动。挖掘阻力对液压挖掘机的稳定性、效率、设备损耗和安全性都具有重要影响。理解和管理挖掘阻力可以帮助优化挖掘机的设计和操作,提高工作效率,延长设备的使用寿命,并确保工作的安全性。
挖掘阻力的研究涉及实验研究、数值模拟、传感技术等多个方面。陈进等[1]在LS-PREPOST 软件中建立铲斗- 土壤模型,以实际实验铲斗轨迹为仿真运行轨迹,通过对比仿真得到挖掘阻力载荷谱。Karmakar与Kushwaha[2]从计算流体力学角度分析土壤粘塑性流变特性及其与工具作用引起的土体变形。文献[3]、文献[4]将铲斗内增加的土壤部分从静态到并入铲斗跟随铲斗运动引起的惯性力引入土楔受力模型,进一步完善工具- 土壤相互作用力分析模型。现有传感器很难直接测试得出挖掘阻力,郁录平等[5]设计专门的销轴传感器测量斗杆与铲斗铰接处的销轴受力,并根据所测受力数据和铲斗工作姿态计算铲斗受力。
在实际作业过程中,研究人员比较关注法向挖掘阻力与切向挖掘阻力之间的关系,文章[6]参照平楔刃模型,将法切比看作定值。本文借鉴参考文献[7]的研究思路,将挖掘过程中的复杂力系等效为一对相互垂直的力和一个阻力矩,建立了阻力系数和阻力矩系数两个数值指标。基于统计学对相关参数进行统计分析。
1 挖掘阻力分析
1.1 单次挖掘分析
挖掘阻力的本质是土壤与挖掘机之间的相互作用所决定的。因此,基于某机型2M土方挖掘的工况下的实验数据,展开对挖掘阻力的研究。参考文献[7]将其看作一个随时变化的复杂力系,不考虑侧向力时,由于挖掘机的对称性,该复杂力系可看作平面力系。将其合成为作用于铲斗切削刃中间位置J 点的切向阻力Ft、法向阻力Fn和阻力矩Tr。
图1 为2M土方挖掘工况下的某单次挖掘中法向阻力、切向阻力、阻力矩以及挖掘阻力合力随时间的变化规律。挖掘动作以切削为主,挖掘阻力的主要组成部分必然是切向阻力。从图中可以看出,挖掘阻力合力规律曲线与切向阻力规律曲线变化相似,在挖掘过程中切向阻力和挖掘阻力合力增减趋势几乎一致,数值存在一定间隙但差距整体不大。同时不难看出在挖掘的初始阶段两者规律曲线高度重合,随着挖掘的进行在数值上才渐渐出现差距。

图1 2M 土方挖掘阻力随时间变化曲线
法向阻力规律曲线整体呈现从零值附近开始递增的趋势,这就导致挖掘阻力合力与切向阻力两者规律曲线先合后分。显然法向阻力也是挖掘过程中不可忽略的组成部分。此外,仔细观察可以看出阻力矩和挖掘阻力合力两者曲线变化类似于反向对称。
1.2 多次挖掘分析
由于切向力是理论挖掘力的重要组成部分和关键性能指标,因此与切向力对应的切向阻力被选作研究参考对象。以切向阻力Ft作为参考,研究法向阻力Fn和阻力矩Tr的变化特性。令ε=Fn/Ft,δ=Tr/Ft,其中ε为阻力系数,δ 为阻力矩系数。该方法确保通过对比分析详细了解挖掘现象的复杂性,以便深入了解挖掘阻力各组成部分的变化规律。
图2(a)为多次挖掘过程中阻力系数随时间的变化规律。图中黑色方块线图代表多次挖掘在对应时刻点的阻力系数值。从图中可以看出,阻力系数大部分值均位于-0.5 至1.5 这一区间内。正方形灰色粗实线表示每个时刻点处所有阻力系数的平均值,受峰值影响绕某条斜率为正的直线波动。同理从图2(b)中可以看出,挖掘阻力矩系数大部分值均位于-0.1 至0.5 这一区间内,阻力矩系数均值线整体位于零值线下方且反向增大。
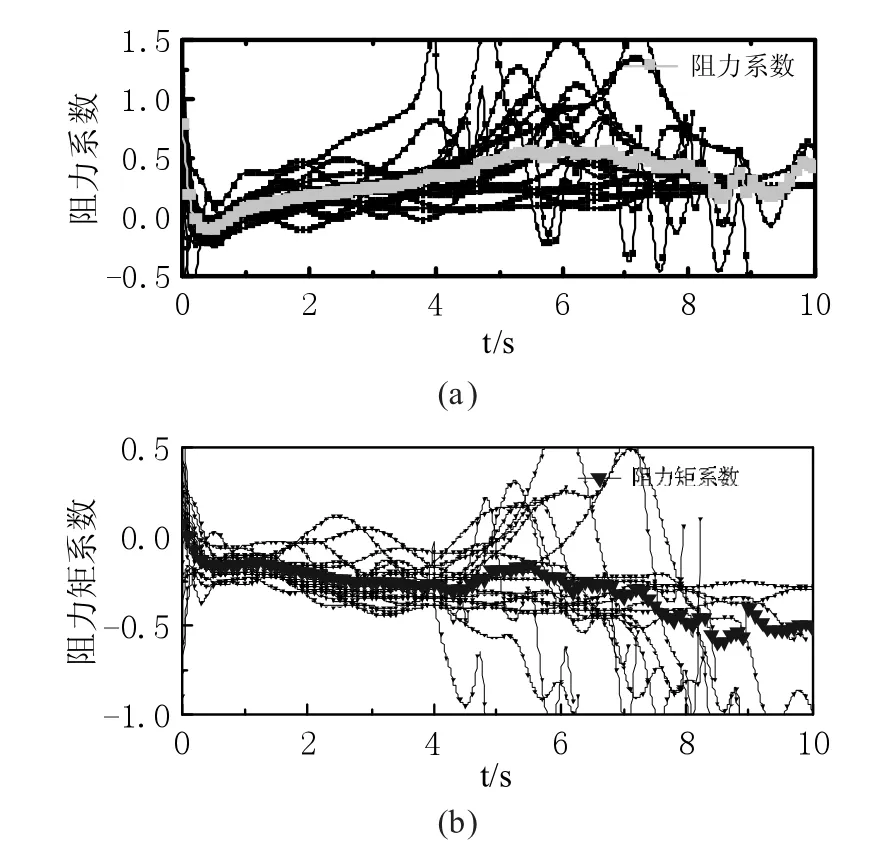
图2 系数随时间变化曲线
阻力系数的计算涉及到了切向阻力,法向阻力,最初学者用一个固定的比值对其进行描述,但挖掘阻力是一个复杂的动态指标,阻力系数也应该是一个动态的变化值。为反映真实挖掘过程中的挖掘阻力,阻力矩的存在同样不应该被忽略,并且阻力矩与切向阻力的比值也应是随时间而变化。切向阻力是挖掘阻力的主要组成部分,这就导致阻力系数值以及阻力矩系数值在一个较小的比值区间内波动。另一方面,随着铲斗翻转装土动作的完成,斗杆和铲斗液压缸主动作用减弱,动臂液压缸主动作用用于提升物料,在这个阶段切向力较小,因此挖掘过程末端比值会达到一个相对较大的峰值。
阻力系数和阻力矩系数的研究是为了了解阻力变化规律,大量统计数据所呈现的变化趋势证明两者的规律确实有迹可循。如果进行更详细的数据分析,相信这一规律会更加清晰。为得到二者系数更详细的分布特征,采用统计学的方法计算阻力系数和阻力矩系数在对应区间的分布概率,统计结果表明阻力系数ε、阻力矩系数δ 的主值区间以及区间分布概率具体情况如表1 所示。

表1 系数区间分布
从表1 中可以看出,就阻力系数ε 而言,主值区间为(-0.2,0.9),但集中程度达到91%。相比ε,2M挖掘δ 主值区间为(-0.9,0.3),并且区间分布概率同样达到91%。阻力系数及阻力矩系数本质是以切向阻力为参考计算法向阻力、阻力矩与其的比值,又因为切向阻力作为挖掘阻力的主要组成部分,所以考虑在不同挖掘阻力范围内探究二者的主值区间显得很有必要。
表2 和表3 为不同挖掘阻力范围下的系数分布具体情况,从表中可以看出挖掘阻力的改变使得主值区间的集中程度发生较大变化。当F>F 时,ε 落在主值区间的概率提升2%,δ 落在主值区间的概率提升7%。当F 表2 不同阻力下ε 区间分布 表3 不同阻力下δ 区间分布 统计数据结果表明ε 以及δ 存在确定的主值区间。另一方面,挖掘阻力较大主要体现在稳定执行挖掘的阶段,无论是阻力系数还是阻力矩系数,其主值区间范围整体保持一致,在挖掘阻力较大时,取值更为集中。此外,δ 的主值区间范围受挖掘深度影响有所变大,考虑今后进一步开展相关实验,完善对其的研究,但整体来说区间变化保持一致。 从表4 中可以看出阻力角θ 的主值区间为(-10,40),当F>F 时,θ 落入主值区间的概率都高达在90%;当F 表4 不同阻力θ下区间分布 表5 不同阻力Δθ区间分布 阻力的变化与各构件的角速度存在相关性,阻力增减趋势与各构件角速度变化趋势有相关性。尽管挖掘机工作运行速度相对缓慢,但考虑其自身较大的自重带来的运动惯性,那么动臂、铲斗及斗杆作为挖掘机的前端工作装置,其运动速度势必会对挖掘过程造成影响,铲斗作为末端执行器,其角速度变化特征必然与挖掘阻力有紧密联系,铲斗直接接触土壤,铲斗角速度的变化直接反映了挖掘机的动态挖掘过程。对多次挖掘中铲斗回转角速度ω1进行数据统计分析,得到其在不同阶段的分布情况(见表6)。 表6 不同阻力ω1 下区间分布 铲斗回转角速度ω1的主值区间为(-0.5,0.1),当F>F 时,ω1落在该区域的概率几乎接近100%;当F 动臂、斗杆及铲斗相互联结,以铲斗回转角速度ω1作为参考,统计研究动臂回转角速度ω3与ω1之前的差值 △ ω3=ω3-ω1,斗杆回转角速度ω2与ω1之间的差值 Δω2=ω2-ω1。动臂角速度差值Δω3为(-0.1,0.5),斗杆角速度差值Δω2为(-0.2,0.4),同时当F>F 时主值区间高度集中。当F 表8 不同阻力Δω2下区间分布 探究挖掘机前端工作装置各构件角速度的规律,结果表明ω1以及角速度差值Δω 有稳定的主值区间,挖掘阻力的变化仅仅会造成其取值概率的波动,这说明挖掘机在不同阶段下的运行角速度较为稳定。另一方面,ω1、Δω2以及Δω3都存在与之匹配的主值区间,这将为动态理论挖掘力的计算奠定数据基础,因为动态理论挖掘力必定涉及到速度这一动态变量,主值区间便很好解决了速度变量取值未知这一难题。此外,不同机型其相应的主值区间或许会有所不同,要想发掘更普遍、更准确的动态规律还需要开展更多的实验,收集更全面的数据。 本文利用统计学对某机型2M土方挖掘产生的实测数据进行了分析,分析了相关参数的分布情况以及不同阻力下的区间分布变化。阻力变化会改变参数分布的集中程度,当挖掘阻力较大时,阻力参数高度集中在某个区间内,这意味着此区间的数值与实际阻力的匹配程度较高,较大程度上能够反映出阻力的真实规律。同时挖掘机前端工作装置构件的回转角速度在不同挖掘过程、不同阶段中保持稳定。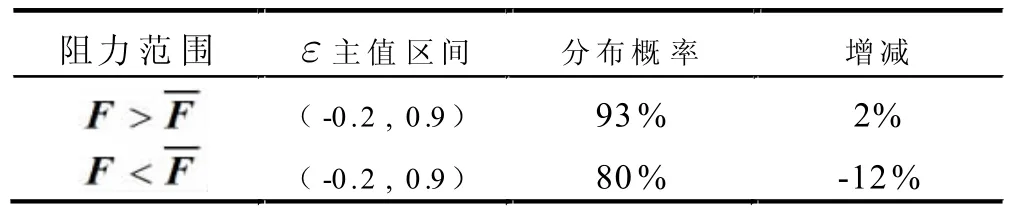

2 挖掘阻力方向分析


3 挖掘阻力的动态特性


4 结论

