主机吊装出舱结构安全性评估方法研究
徐 博,蔡诗剑,李 顺,殷俊俊
(1.中国船舶及海洋工程设计研究院,上海 200011;2.上海市船舶工程重点实验室,上海 200011)
主推进柴油机(简称主机)作为船舶的重要设备,对其进行保养和维修工作是必须要面对的问题。根据目标船主机全寿期维修保障大纲的要求,主机工作一定时长需进行修理,一般采用原位拆检,不需要整机出舱,只有当主机重要部件(如曲轴)损坏时,才需返厂换修并进行台架试验。但是在紧急情况下,原位拆检修理周期长,无法满足需求,整机换装是首选方案。主机出舱需要结合该船的结构形式、承修厂拆装工艺的复杂性和主机的相关参数,制定周密的出舱方案,必然要考虑舱内吊装问题,对吊装出舱过程中工装设施和船体结构进行安全性评估。一直以来,国内外关于船舶主机出舱设计和评估方面的研究较少。杨京华等[1]开发设计出一种可组合式主机缸体总成设备吊装工装;陈文战等[2]对燃气轮机吊装轨道系统开展了受力分析;边超斐等[3]从工法和工艺的角度对设备吊装出舱进行介绍,并对舱内吊装区域进行了强度分析;孔宁等[4]指出吊装过程,眼板附近或较大开口结构会出现应力集中现象,需要对模型适当简化处理。二维或三维梁系模型相比有限元板梁模型简化程度高,也常用于甲板支撑构件评估,如DNV的3D-BEAM 软件,以矩阵位移法和铁木辛柯梁理论为基础,可计算平面梁系及三维空间梁系的响应。高处等[5]在使用3DBEAM 评估车辆甲板门式钢架结构时,发现端部剪应力和有限元模型结果存在较大差异,分析指出在评估剪应力时,梁系模型计算结果偏危险。
由于主机通过多根吊索实现横向、纵向移动,出舱路线复杂,存在多种工况组合的情况,因此选择适合的规范进行评估是必要的,但是目前国内外缺少相关规范指导。并且主机移动是通过工人操作手拉葫芦实现的,吊索在交替使用过程中,容易发生吊索失效或受力不均的情况,影响了吊装区域的结构、设备甚至人员安全,如何考虑安全系数是吊装评估的难点。另外,由于本船特殊的内部设计,选择合适的简化计算方法也是十分重要的,文章以有限元直接计算作为对比,对单跨梁和三跨梁理论的适用性做了论证,为指导主机吊装作业提供了理论依据。
1 主机吊装出舱工装设计
1.1 整机出舱方案
本船在前机舱右舷、后机舱左舷各布置2 台主机,每台主机质量为105 t。移出路线方案需要综合考虑各方面的因素,使拆装工程对船的影响最小。图1 为水平方向主机出舱路线示意图,在2#、3#、4#主机上方甲板都可直接开口,主机经吊索垂直吊至坞舱后,然后横向移动至小车处;1#主机上方甲板由于无法开口直接吊出,需要先将2#主机吊装出舱后,在机舱内通过横移工装至2#主机处,然后再通过吊索吊装出舱;当3#、4#主机都需出舱时,只在3#主机上方甲板开口,4#主机也需要通过横移工装至开口下方,通过吊索吊装出舱。考虑到结构的安全性,小车停放在距离开口较远的坞舱纵舱壁处,这也导致4台主机在坞舱内吊装横移时工况较多,需要布置足够多的吊点。

图1 水平方向主机出舱路线示意图
1.2 眼板布置
通过固定在强横梁上的眼板用吊索将主机从机舱内垂直起吊至坞舱,采用2组吊索交替使用的方式沿着船体横向移动,同一时间仅有1 组吊索(8 根吊索)受力,图2 为主机起吊示意图。主机正上方的4 根横梁上设置吊点,横向2 个吊点之间的距离通常略大于主机上吊点宽度,并据此合理布置眼板间距。相邻眼板之间的横向距离为0.8 m,2个吊点之间的横向距离为2.4 m。眼板根据GB 7029-86《船用眼板》选取。

图2 主机起吊示意图
1.3 主机舱内横移工装设计
主机在机舱内向工艺开口进行横向移动时,需在主机下方设置导轨座、导轨梁、圆钢和主机托架。导轨座焊接在内底板上,与主机基座错开,其顶部高于主机基座顶部;导轨梁放置在导轨座上,横向布置;圆钢放置在导轨梁上,纵向布置;主机架在主机托架上,再放置在圆钢上,通过圆钢的滚动实现横向平移。
1#主机和4#主机经2#工艺开口出舱时,涉及到主机在机舱内横移问题。新建导轨基座1、2、3 作为受力点,避免主机基座因承受主机重力而产生变形,导轨梁与主机基座之间的垂直距离为h,根据实际施工情况确定h大小。以导轨基座为支撑点,沿船体横向设置4根工字钢作为轨道,在每条导轨上沿船体纵向放置圆钢,主机舱内横移示意图如图3所示。

图3 主机舱内横移示意图
2 主机吊装甲板主要构件安全性评估
2.1 校核衡准
通过梳理主机吊装出舱过程中安全评估涉及的相关规范,考虑到设备吊装的场景与船舶起重设备工作场景较为接近,所以在《船舶与海上设施起重设备规范》(以下简称《规范》)中“3.10.7.1强度衡准”的基础上,从其它规范中补充挠度衡准,对比后采用较为保守的劳氏军规《LR Rules and Regulations for the Classfication of Navel Ships》挠度比要求。
许用弯曲应力[σ]为:
式中,σs为材料屈服强度,本文取235 N/mm2;n1为弯曲应力安全系数,取1.67。
经计算,[σ]=141 N/mm2。许用剪切应力[τ]为:
式中,n2为剪切应力安全系数,取2.50。
经计算,[τ]=94 N/mm2。挠度比[f]为:
式中,ω为梁的挠度;l为横梁支撑点之间的距离。
2.2 载荷安全系数分析
在主机出舱时,眼板所在甲板上仅有少量设备,因此忽略甲板上的设备重量和载荷。另外主机吊装在舱内操作,吊升过程非常缓慢平稳,而且受力眼板位置与设备吊环位置基本一致,眼板主要承受垂直向下的载荷,即主机自身的重量。考虑单台主机105 t 产生的载荷,单个吊点的平均静载荷为131.25 kN。
实际操作中可能存在动载荷、受力不均匀及意外情况,实际载荷可表示为静载荷乘一定的安全系数。对于目标船吊装工况,设备自重、船舶倾斜和其他水平力暂不考虑,参考《规范》,起升载荷可表示为:
式中,F′为起升载荷;P为设备静载荷;φh为起升系数,指在起重设备工作时,考虑所有动载效应的系数,参考龙门式起重机,φh取1.15;φd为作业系数,指考虑起重设备作业频次与载荷状态的余度系数,参考龙门式起重机,φd取1.05。
同时,也要考虑主机移动过程中,8 根吊索存在某一根吊索失效的极端情况(《规范》中没有考虑这种情况)。将主机重心位置和受力眼板端部通过多点约束(MPC)连接,主机重量通过集中力的方式模拟,加载在8个眼板的几何中心,高度距离下甲板1 m 的位置。模拟端部或者中间位置一根吊索失效的情况,吊索失效水平示意图见图4,周围圆圈表示受力的吊索,中间椭圆表示主机中心。
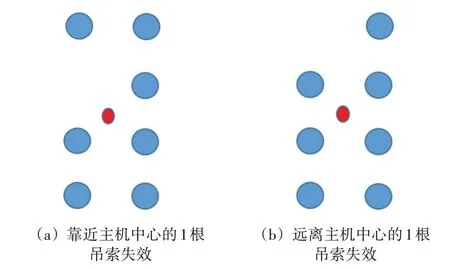
图4 吊索失效水平示意图
定义意外载荷系数φf:
式中,Fmax为某根吊索失效情况下,计算得到的眼板最大MPC受力;Fave为8根吊索均匀受力情况下,计算得到的眼板平均MPC受力。
经计算,图4(a)中φf=1.448;图4(b)中φf=1.616。
综合以上分析,吊装评估统一取安全系数C为:
另外,由于起升载荷包括起重设备安全工作负荷与起重设备运动部件自重之和,需要包含手拉葫芦和吊索重量,将设备重量计入安全系数内统一考虑,最终C取2。
故该船单个吊点实际加载的力F为:
2.3 基于梁理论计算方法的结构安全性评估
上甲板板架可简化成甲板纵桁和甲板强横梁组成的交叉梁系结构。由于目标船甲板纵桁的跨度很长,其对强横梁的支撑很弱,因此可忽略甲板纵桁的支撑作用,仅考虑强横梁。
1)模型要求。对于甲板板架结构,重点考虑主要构件的强度,需要将主要构件简化成梁模型。主要构件的带板对梁的抗弯能力有重要作用,需要反映在梁模型中。本文校核的横梁长度为22.184 m,两侧纵舱壁间横梁长度为17.4 m,横梁结构剖面为T 型材,甲板横梁间距为2 m。参考《钢制海船入级规范》,以横梁腹板为基准,沿船首和船尾方向各取1 m作为T型材的带板。
2)单跨梁理论计算方法。基于该船特殊的内部设计,坞舱两侧纵舱壁和支柱对强横梁有较强的约束,将强横梁简化为端部位于纵舱壁、边界条件为固支的单跨梁,在跨内承受2 个集中力作用,单跨梁弯曲简化过程如图5所示。横梁的应力和挠度查弯曲要素表可得。
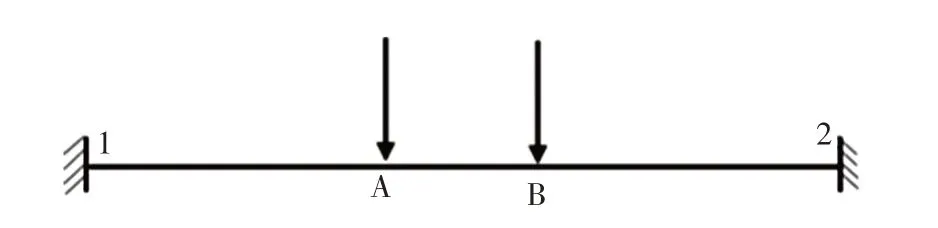
图5 单跨梁弯曲简化过程
3)三跨梁理论计算方法。基于强横梁两端与强肋骨连接,端部采用刚性固定,纵舱壁加支柱对横梁起到支撑作用,但是抗弯能力有限,因此将强横梁简化为两端固支且有2个自由支座的三跨梁,在中间跨承受2个集中力作用,三跨梁弯曲简化过程如图6所示。
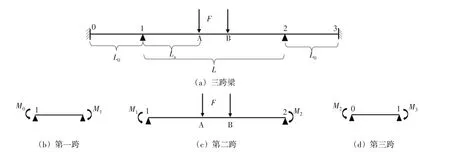
图6 三跨梁弯曲简化过程
分析结构,该三跨梁为4 次静不定结构,因此有4 个未知量,采用“力法”[6]进行求解,去除多余约束将静不定梁化为静定结构,根据变形连续条件,在去掉约束加上约束反力矩的地方建立变形连续方程式如下:
式中,E为弹性模量;I为梁截面惯性矩;L为支座1、2 之间的距离;La、Lb为集中力加载位置A、B到支座1 的距离;L′a、L′b为集中力加载位置A、B到支座2的距离,La+L′a=Lb+L′b=L,Lb=La+2.4;L0为支座0、1 和2、3 之间的距离;M0、M1、M2、M3为约束反力矩。
联立解方程可求出约束反力矩M0、M1、M2、M3,进而计算得到横梁的应力、挠度。
2.4 基于有限元计算方法的结构安全性评估
1)模型要求及边界条件。模型范围选取的原则为:纵向为吊装区域前后至少延伸3 个强框间距;横向取整个船宽;垂向为吊点处甲板和其下层甲板之间部分,建立有限元模型。
详细建立板、横梁、纵桁、纵骨和支柱等结构的几何模型,对甲板、纵舱壁和T型材腹板以及眼板所在区域的T型材面板采用四边形单元,网格大小保证强横梁面板能划分4 个网格;其他T 型材面板、纵骨及支柱结构用梁单元代替;眼板进行简化处理,可用板单元模拟其基本大小,不做开口。网格尺寸为100×100。
模型与下层甲板和船体外板刚性连接,在模型底部和甲板舷侧端施加位移约束,模型前后端采用对称边界条件(垂直于端面方向的线位移为0,绕端面内两坐标轴的角位移为0)。
2)载荷施加。吊钩与眼板处的接触应力很难通过有限元来模拟,实际吊装过程中主要根据吊装载荷来选取对应型号的眼板,以满足其强度。在有限元中,以集中力的形式将载荷施加在眼板下端,加载在单个眼板上的垂向力大小为262.5 kN。吊装有限元模型及载荷施加如图7所示。
3)工况设置。按照出舱路线,对4 台主机从起吊到移动到指定位置过程中的每一步均设置工况进行受力分析。
4)结果读取。采用有限元分析软件MSC Nastran 计算强横梁的应力和挠度,强横梁弯曲应力读取自板单元面内正应力,剪切应力读取自板单元面内剪切应力。
2.5 梁理论计算和有限元计算结果对比分析
将主机吊装出舱可能存在的全部工况(La为0.7~14.3 m,步长0.8 m),梁理论计算和有限元计算结果对比如图8所示。从图8可以看出,单跨梁结果与有限元结果相差较大,表现为正应力偏大,挠度偏小,说明将强横梁简化为固定在坞舱纵舱壁上的单跨梁是不合理的,由于边界条件过强,导致计算得到的正应力过大,梁的变形偏小,结果和实际情况不符。

图8 梁理论计算和有限元计算结果对比
三跨梁和有限元计算的弯曲正应力曲线变化趋势相同,两者得到的最大弯曲正应力对应的工况都是La为4.7 m 或10.3 m,而且横梁最大正应力出现在和支撑纵舱壁连接处,三跨梁模型弯曲正应力水平要比有限元模型高,误差在13%以内。三跨梁模型和有限元模型的最大剪切应力对应的工况都是La为0.7 m 或14.7 m,而且横梁最大剪应力出现在集中力加载位置和支撑纵舱壁之间,有限元剪应力要比理论模型高,误差在14%以内。三跨梁和有限元计算得到的最大挠度比非常接近,误差在11%以内,当La为7.1 m 或7.9 m 时,三跨梁计算和有限元计算都取得最大挠度。而且从图8中可以看出,横梁挠度的安全裕量相对是最小的,换言之,强横梁的安全性主要取决于挠度是否满足衡准。
总的来说,主机吊装安全性评估,基于三跨梁模型得到的结果与有限元结果吻合较好,在误差允许的范围内,三跨梁模型推导的应力和变形结果是安全可靠便捷的。
三跨梁模型为指导主机吊装方案的制定、吊装作业的开展提供了理论依据。根据该方法,通过编写Excel 表可快速计算大量工况,进一步可找到最大正应力、最大剪应力、最大挠度对应的工况并进行校核。以本船主机吊装方案为例,La为4.7 m 工况下的最大正应力、La为0.7 m 工况下的最大剪应力、La为7.1 m 工况下的最大挠度是吊装过程中的代表工况,只要满足衡准就能保证结构的安全。也可以进一步通过理论计算反推,3 个工况对应的临界载荷分别为357 kN、668 kN、345 kN,只要保证单根横梁单个吊点载荷不超过345 kN,也能保证结构的安全。
根据上述对比分析,三跨梁模型和有限元计算都能进行主机出舱结构安全评估。有限元方法成熟、可靠,但是需要耗费大量的时间建模分析;理论计算是根据梁理论和以往有限元计算经验,将吊装的主要受力构件简化成三跨梁模型,可针对吊装工况进行快速的计算,且便于模型的修改和重复计算。通过上文对梁理论和有限元计算结果的对比,也验证了三跨梁理论模型的合理性和可靠性。因此,三跨梁模型可用来评估目标船主机吊装出舱过程中强横梁的安全性。但是值得注意的是,如果板架的纵向长度较短,则纵桁的支撑作用不能忽略,这种情况下,上述简化计算方法不太适用,需要采用梁系计算方法进行计算。
3 结束语
主机尺寸大、质量大,出舱路线复杂,为了保证吊装的安全性,吊装出舱过程中结构安全性评估是十分必要的。通过梳理相关规范,为大型设备出舱方案的制定提供依据,提出了主机吊装出舱过程中船体结构强度、刚度的直接计算方法(包括梁理论计算方法和有限元计算方法)。并以目标船为研究对象,通过开展主机出舱过程中,船体结构的载荷分析、强度和刚度计算,对吊装方案的安全性进行了评估,得出以下结论:①针对主机吊装提出的出舱和工装方案,为类似设备出舱转移提供参考;②针对多根吊索起吊的大型设备吊装作业,提出了确定意外载荷系数的方法;③主机吊装出舱方案安全性满足要求,单跨梁模型与实际情况不符,三跨梁和有限元计算结果吻合较好,建议编写Excel 表,可显著提高计算效率,三跨梁模型计算方法为指导吊装作业提供了理论依据;④由于目标船甲板纵桁的跨度很长,其对强横梁的支撑很弱,因此可以忽略甲板纵桁的支撑作用,仅考虑强横梁。如果板架的纵向长度较短,则纵桁的支撑作用不能忽略,这种情况下,单梁理论计算方法不太适用,需要采用梁系计算方法进行计算。

