双边聚磁式槽口型永磁直线电机多目标优化研究
夏奥妮,张文龙,王 滢,许义景,石 煜,孔德坤,杨天乐
(1.西南交通大学 电气工程学院,成都 611756; 2.株洲中车时代电气股份有限公司,株洲 412001)
0 引 言
永磁直线同步电机凭借可控性好、效率高、推力密度高等优点,在轨道交通、装备制造等领域有很大的发展空间。而传统永磁直线电机(以下简称PMLM)将电枢和磁极分别放在动子、定子侧,推力波动大,永磁轨道成本高昂且需要全行程铺设,另外需装设隔磁装置[1]。初级励磁型 PMLM 则是将电枢绕组和磁极均放在初级侧,次级侧仅由铁心构成,永磁体用量大幅减少且无需隔磁装置,因此它逐渐成为了研究热点[2]。
初级励磁型 PMLM按永磁体所在位置可分为磁通切换型、磁通反向型、游标型、交替型、磁通偏置型、槽口型[3]。其中,聚磁式槽口型PMLM的初级侧齿槽内置有电枢绕组和Halbach永磁体阵列,次级是关于初级对称分布的硅钢片叠压成的铁心,采用并联励磁结构,故该类型电机没有失磁风险且漏磁少,推力密度大,适合用于低速、大推力的场景,但其运行过程中有很大的推力波动和很大的法向力波动,怎样抑制此类电机电磁力波动是一个值得研究的问题。
目前研究发现,造成PMLM推力波动的主要原因是齿槽效应、端部效应、绕组参数不对称、负载特性等,造成法向力波动的主要原因是齿槽效应、端部效应、电枢反应等[4]。而电磁力波动抑制方法一般分为优化电机控制策略和优化电机结构两大类。在电机控制策略优化方面:建立精确的推力数学模型,对推力波动进行前馈补偿;通过神经网络控制算法、自适应控制策略、鲁棒控制等方法来抑制推力波动。在结构优化方面:可以优化极弧系数、优化磁极形状、优化齿槽形状和采用齿靴等来抑制齿槽效应;可以通过优化初级铁心长度、增加辅助极等来抑制端部效应;另外,还可以采用双边结构,大幅降低法向力,进一步降低推力波动。此外,建立准确的优化设计模型对提高电机优化效率至关重要。传统优化模型往往采用有限元法、磁阻网络法和解析法,这些方法需要电磁原理分析,其中有限元法在大量迭代计算的电机优化过程中,需要占用很大内存并且耗时长,而代理模型不用进行复杂分析且计算时间短,常见代理模型有多项式响应曲面法、空间映射等机器学习法[5]。
多项式响应面法采用多元二次回归方程来拟合因素与响应值之间的函数关系,通过对回归方程的分析来寻求最优参数,在电机优化中,设计空间最大维度可达14,也是建模最常用和最有效的方法之一。文献[6]采用Taguchi法对双边永磁直线同步电机参数进行方差分析和灵敏度分析,筛选优化参数,再结合响应面法进行多目标参数优化,使得电机推力波动从7.65%降至5.05%。文献[7]采用响应面法进行有限元仿真,抑制电机端部效应。本文先采用Taguchi模型对目标电机参数进行显著性分析,再结合响应面法,优化主要的电机参数,提高工作效率。
本文从结构优化方面提出一种双边聚磁式槽口型PMLM,分析了气隙磁场调制过程,利用等效磁路法推导电机气隙磁密解析式、推力方程,对电机尺寸进行初步设计,结合有限元软件ANSYS Maxwell,分析了磁极厚度、槽宽、电机叠厚、次级高度等参数对电机特性的影响,以减少推力和法向力波动、保证大推力为优化目标,利用响应面法CCD模型进行多目标优化,最后得到合适的电机参数。
1 电机结构和工作原理
1.1 电机结构
本文的双边聚磁式槽口型PMLM由两边错位的次级结构、初级铁心、位于槽口采用Halbach排列的永磁体和电枢绕组构成,选用6槽5极结构,采用集中绕组形式进行初步研究,电机结构如图1所示。
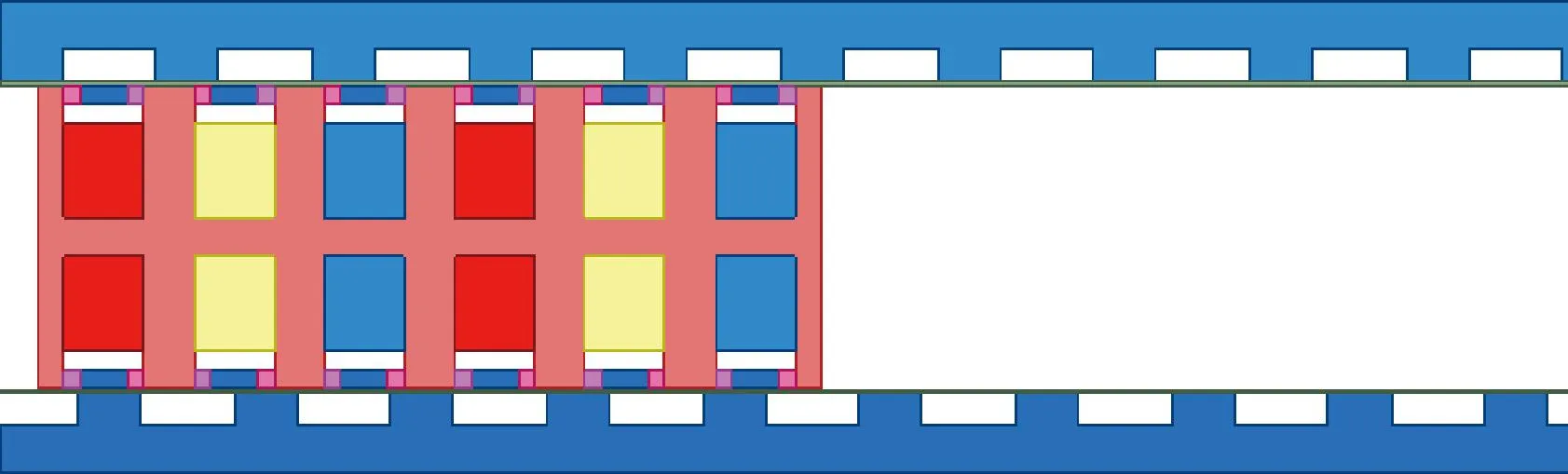
图1 双边聚磁式槽口型PMLM结构
根据长行程传输设计要求,电机额定速度vN=2 m/s,电机总长L=200 mm,绕组为单层集中绕组,其连接图如图2所示。
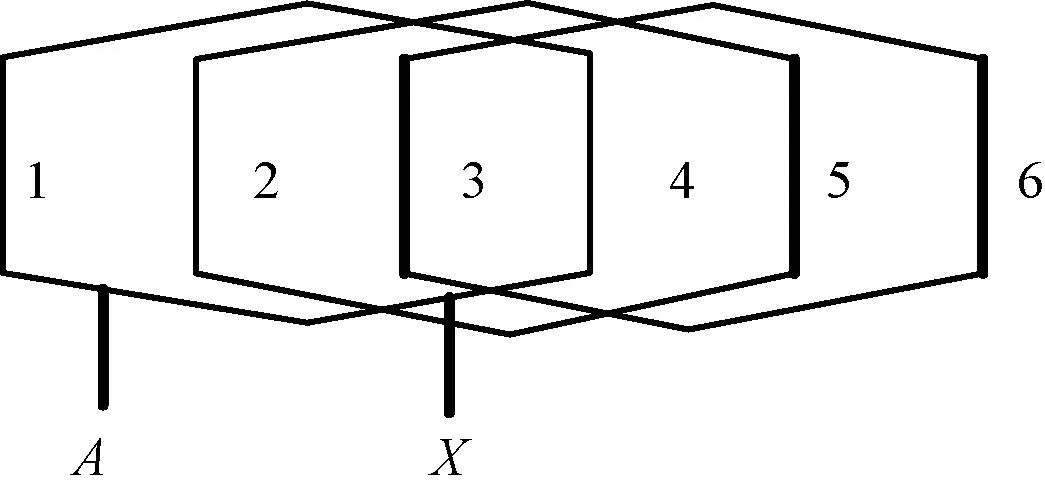
图2 绕组连接示意图
1.2 电机工作原理
双边短初级聚磁式槽口型PMLM采用Halbach永磁阵列,这能够有效减少中间垂直运动方向充磁的永磁体与电枢齿之间的漏磁,提高永磁体的利用率,从而进一步提高电机的推力密度。图3是简化后的磁路模型。
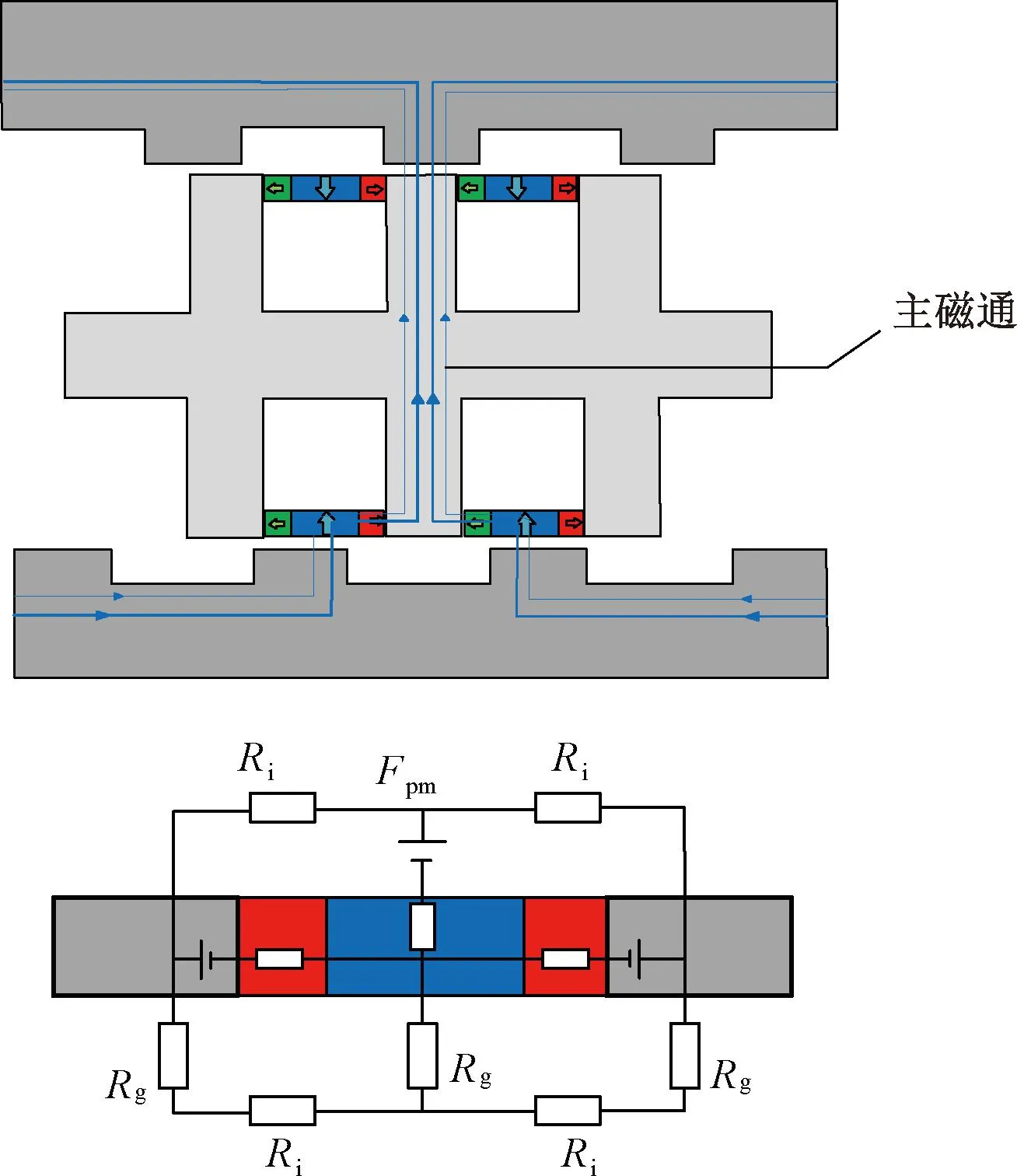
图3 双边聚磁式槽口型PMLM简化磁路模型
直线电机推力的产生主要依靠次级凸极铁心的变磁阻效应,励磁磁场和电枢磁场在气隙处被调制得到可以产生有效推力的行波磁场。对于这种双凸极结构的谐波电机来说,要获得稳定的电机推力,必须满足以下两个条件:(1)永磁体产生的励磁磁场的极对数等于电枢绕组产生的磁场极对数;(2)相同极对数下的磁场运动速度相等[8]。
电枢绕组极对数满足:
(1)
式中:pa为电枢绕组极对数;Npm为永磁体极对数;ps为次级极对数;k,b为系数。
当忽略初级、次级铁心磁阻时,不考虑次级齿槽结构,则气隙磁密Bpm的计算方法如下:
(2)
(3)
(4)
(5)
(6)
式中:Bgm1是垂直充磁永磁体作用下的气隙磁密;Bgmp是水平充磁永磁体作用下的气隙磁密;hpm是永磁体厚度;wpmp是水平充磁永磁体宽度;wpt为初级齿宽;α是永磁体宽度和初级槽距lp的比例;Agm1和Agmp是积分系数。
在考虑次级的齿槽调制作用后,仅永磁体励磁下的气隙磁密Bg:
(7)
(8)
式中:Λrel为考虑次级有槽的气隙相对磁导;Λs为次级有槽时的气隙磁导函数;xs0为次级初始位置。
该电机采取Id=0的控制方法,电磁推力满足下式:
(9)
为了获得较大电机推力,设计初期选择合适尺寸使得磁动势最大化,选择永磁体阵列中水平充磁和垂直充磁方向的永磁体宽度比,可以参考次级无槽下,气隙磁密的基波与二次谐波幅值之和最大所对应的永磁体宽度比,本文选择0.7的永磁体宽度比。参考推力尺寸方程,本文的双边聚磁式槽口型PMLM初始参数如表1所示。
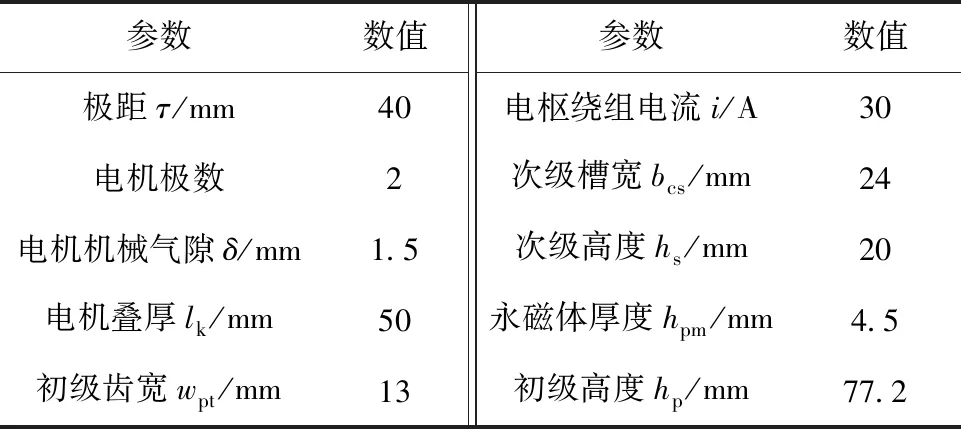
表1 双边聚磁式槽口型PMLM参数
2 仿真分析
根据表1中的参数,搭建基于 Maxwell 的双边聚磁式槽口型PMLM模型,分析其主要结构参数变化的影响,进行初步优化。
设置电枢绕组电流为30 A,额定频率为50 Hz,绕组匝数为30匝,电机运行速度为v=2 m/s。该电机的电磁力受双边次级错位距离影响,首先必须确定合适的双边次级错位距离。图4为电机电磁力和双边次级错位距离的关系图。为了尽量降低法向力的影响,使法向力趋于零,选取τ/2作为双边次级错位距离。
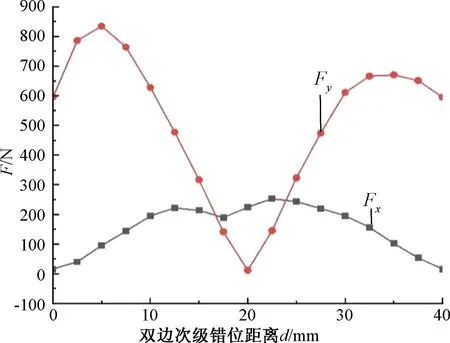
图4 电磁力和双边次级错位距离的关系图
接着,用有限元单变量分析法研究双边次级错开位置、磁极厚度、初级齿宽、次级槽宽、电机叠厚、次级高度和初级高度这6个因素对电磁力的影响。
电机叠厚影响初级、次级铁心饱和程度、励磁磁动势大小和初级电负荷,从图5可以看出,推力大小和法向力波动随着电机叠厚增加而增大,但推力波动变化不大,维持在33%。
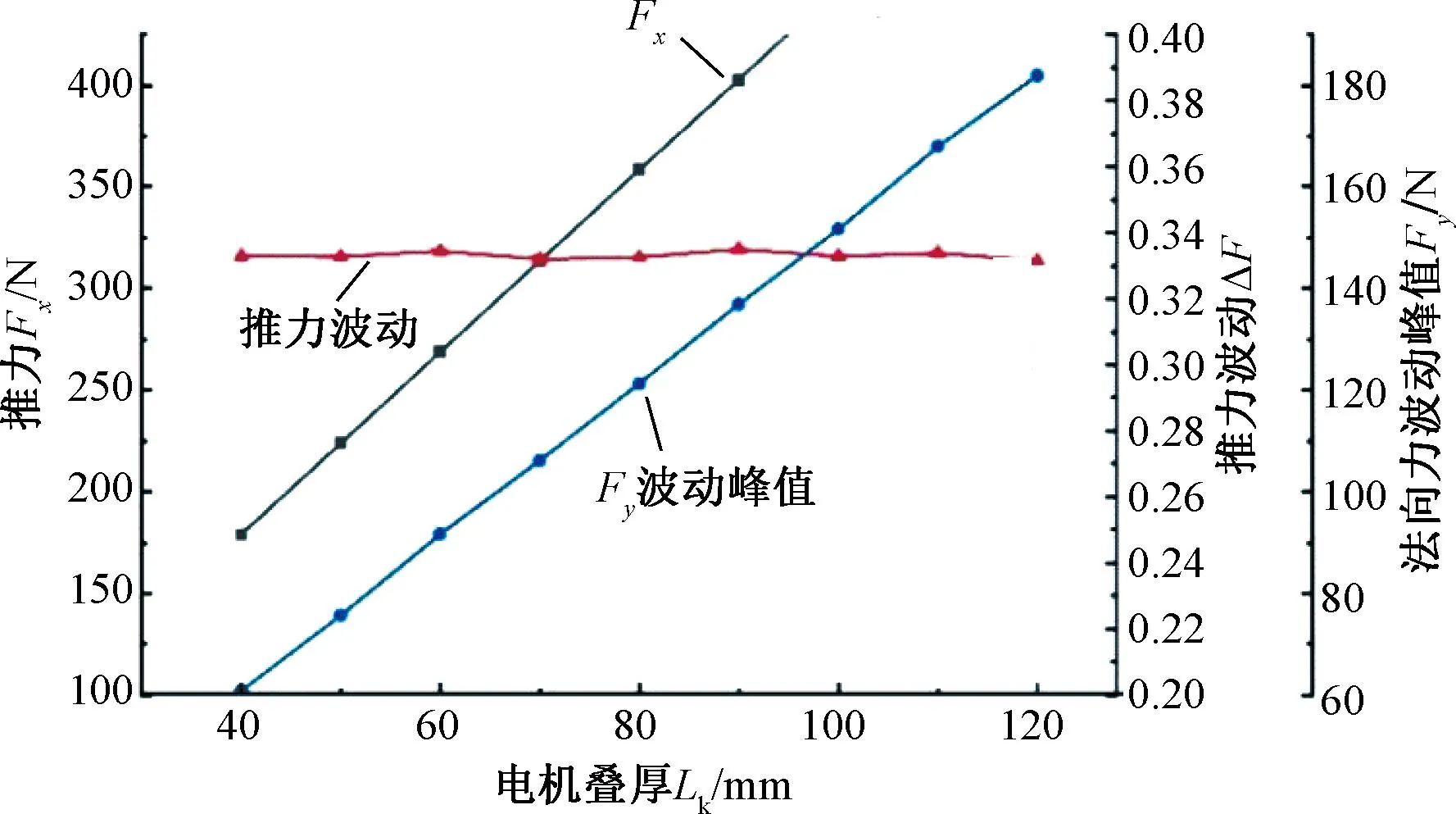
图5 电机叠厚对电磁力影响
初级齿宽影响初级铁心的饱和程度和初级电负荷,若初级齿宽变大,电负荷也需要变大才能提供足够强的磁场,但电枢齿的饱和程度变低。由图6可知,选择wpt=12 mm是比较合适的。

图6 初级齿宽对电磁力的影响
次级槽宽和次级磁导相关,影响着次级凸极铁心对气隙磁场的调制作用,且是一种非线性的关系。由图7可知,次级槽宽取28 mm时,平均推力最大,推力波动和法向力比较小。
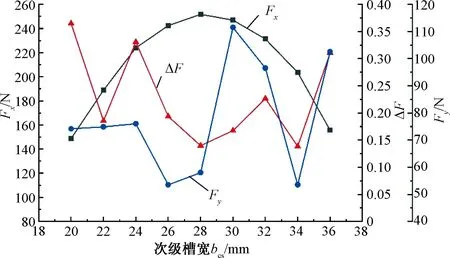
图7 次级槽宽对电磁力的影响
由图8可知,在初级槽深不变情况下,初级高度对电机推力和法向力的影响并不大,因为电机主磁通很少经过中间初级铁心。次级高度hs影响次级铁心的饱和程度,hs越大,次级铁心饱和程度越低,在图9中推力波动和法向力波动越小。
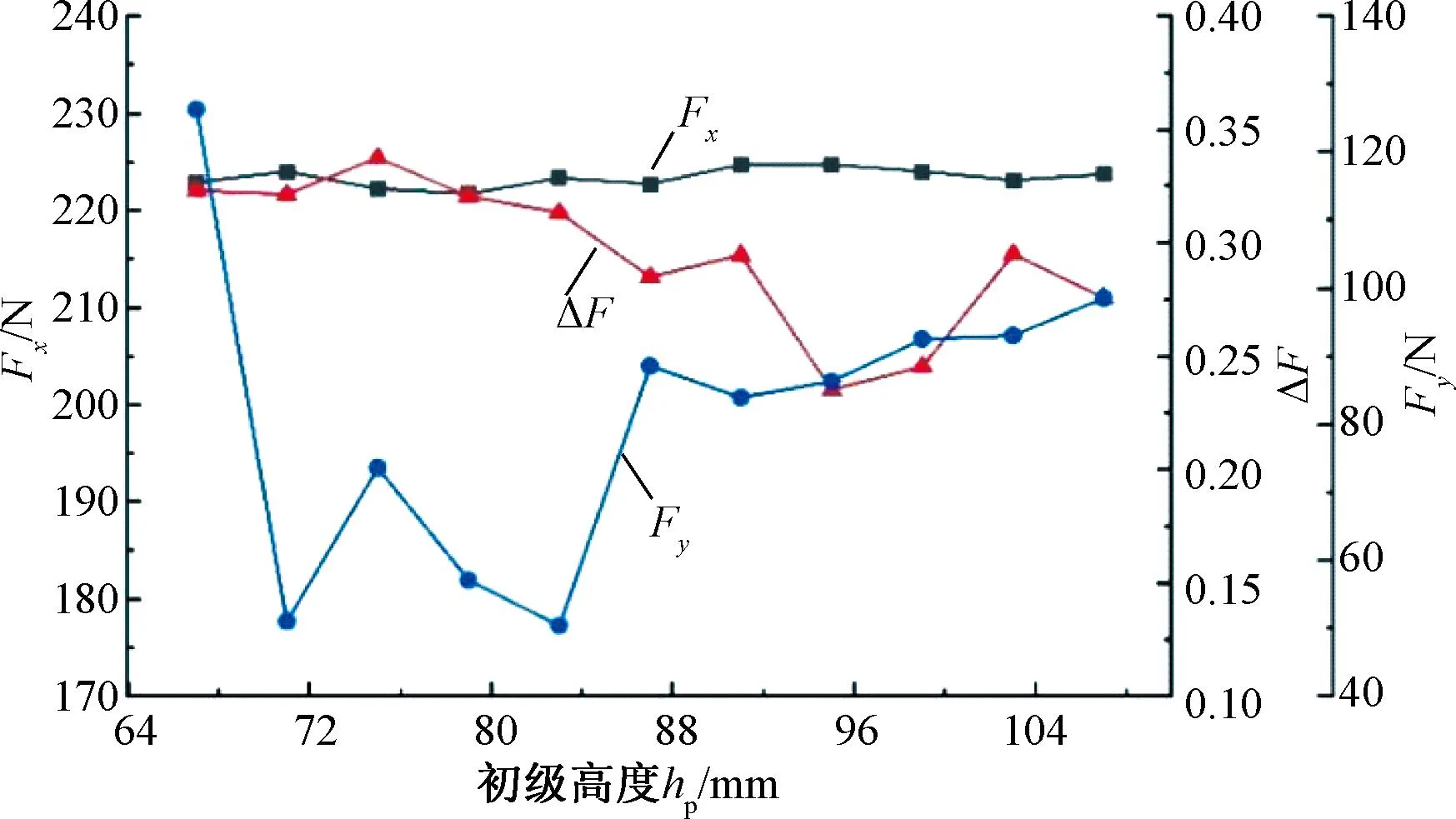
图8 初级高度对电磁力的影响
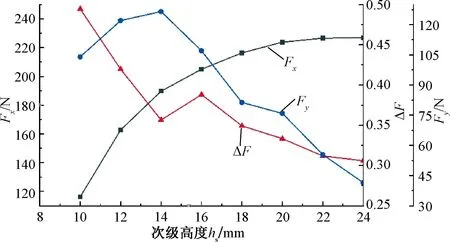
图9 次级高度对电磁力的影响
永磁体厚度影响励磁磁动势、电负荷和铁心饱和程度。从图10可以看出,随着永磁体厚度增加,推力和法向力波动峰值均在上升。
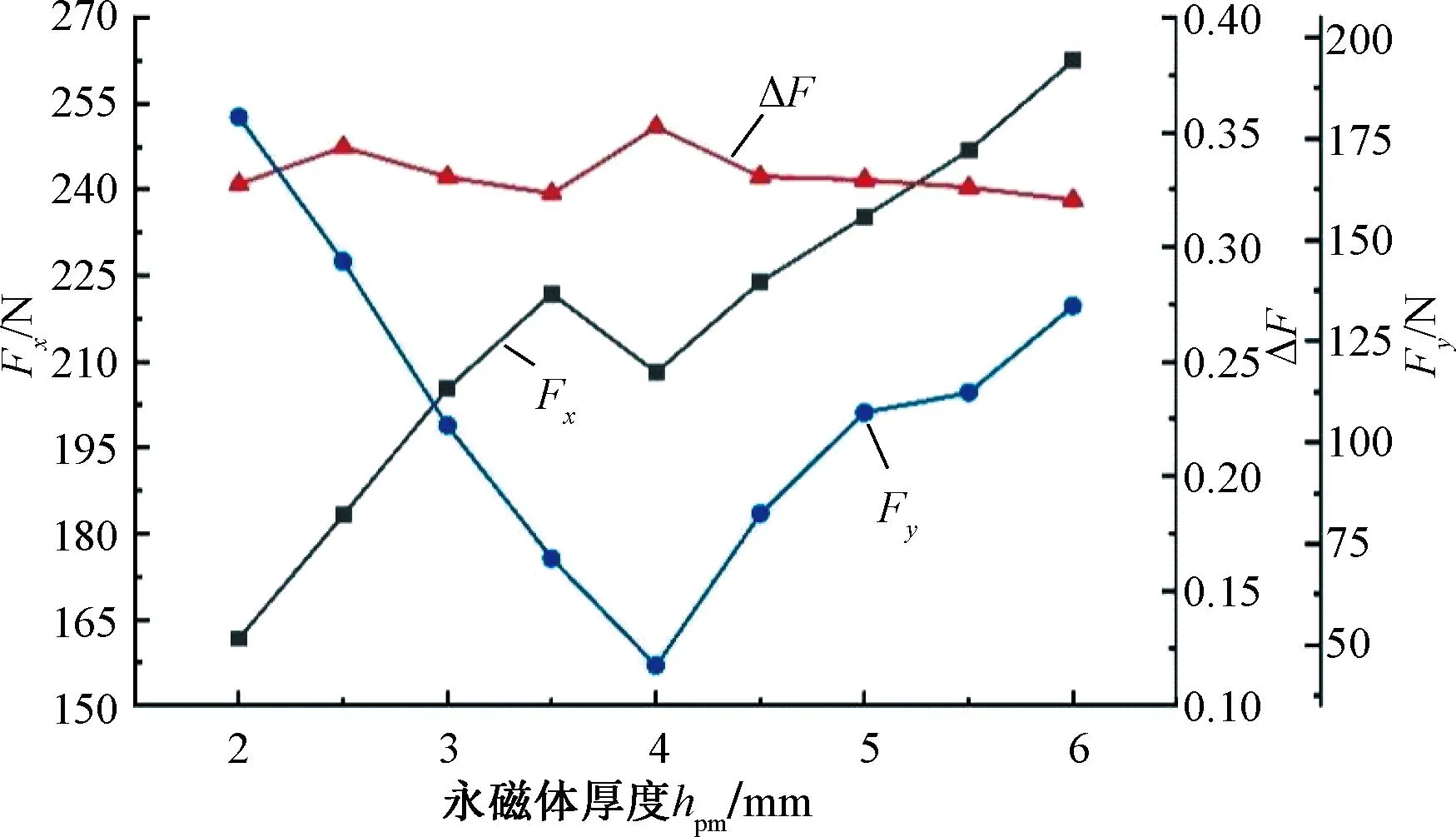
图10 永磁体厚度对电磁力的影响
由单因素有限元分析可知,初级高度对于电机推力的影响不大,可以尽量减小初级高度来降低电机成本,后续只对永磁体厚度hpm、初级齿宽wpt、次级槽宽bcs、电机叠厚Lk、次级高度hs这些因素进行多目标优化分析。
3 多目标优化分析
双边聚磁式槽口型PMLM因两端断开、次级齿槽的调制作用,有很大的推力和法向力波动。推力波动会增大电机的控制难度,对电机运行性能有严重影响;对有机械导轨支撑的结构,法向力波动会通过摩擦力叠加到推力波动里面,法向力波动大还会导致机械部件、导轨发生形变,造成恶劣机床振动。因此,需要优化电机结构参数,以保证推力满足设计要求、降低推力和法向力的波动为优化目标。
3.1 田口法优化设计
为了分析不同电机参数对电机优化目标的影响,结合有限元法和Taguchi模型进行全局分析。田口法是一种基于方差、高效且收敛快速的显著性分析技术。
首先,确定优化目标,在初级铁心用量近似相同且施加相同的电流负荷条件下,保证推力值尽可能大,且推力波动和法向力波动尽可能小,故优化目标个数为3,R1为推力值,R2为推力波动,R3为法向力波动峰值。选取了5个优化因素,以初始参数为参考,变化范围如表2所示。优化因素的水平数为4,确定了16个实验,如表3、表4所示。
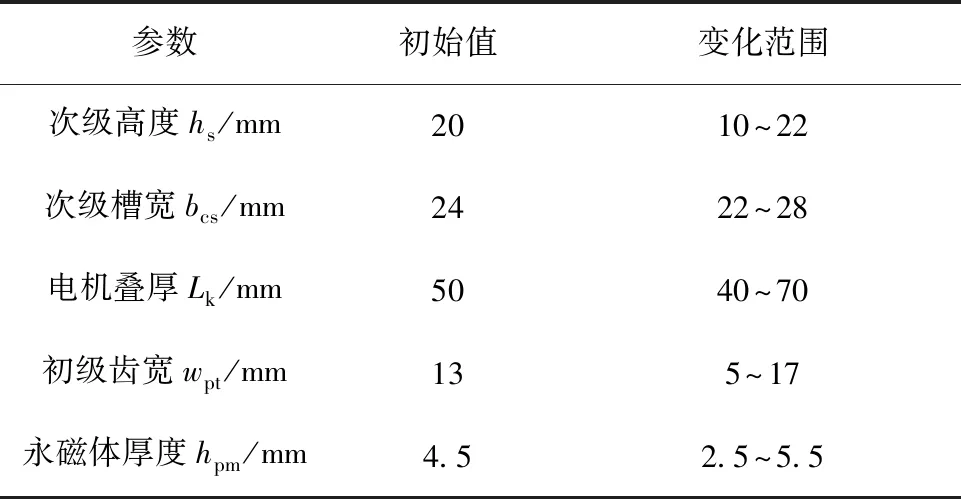
表2 优化变量初始值和变化范围
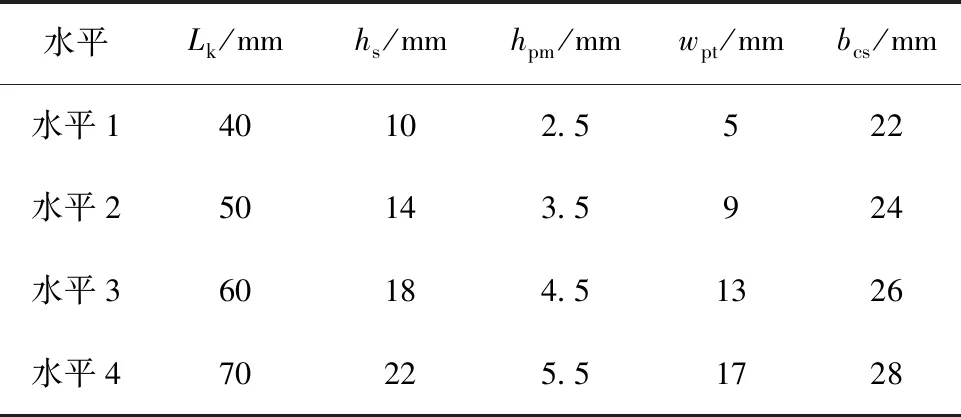
表3 田口法优化参数与因子水平
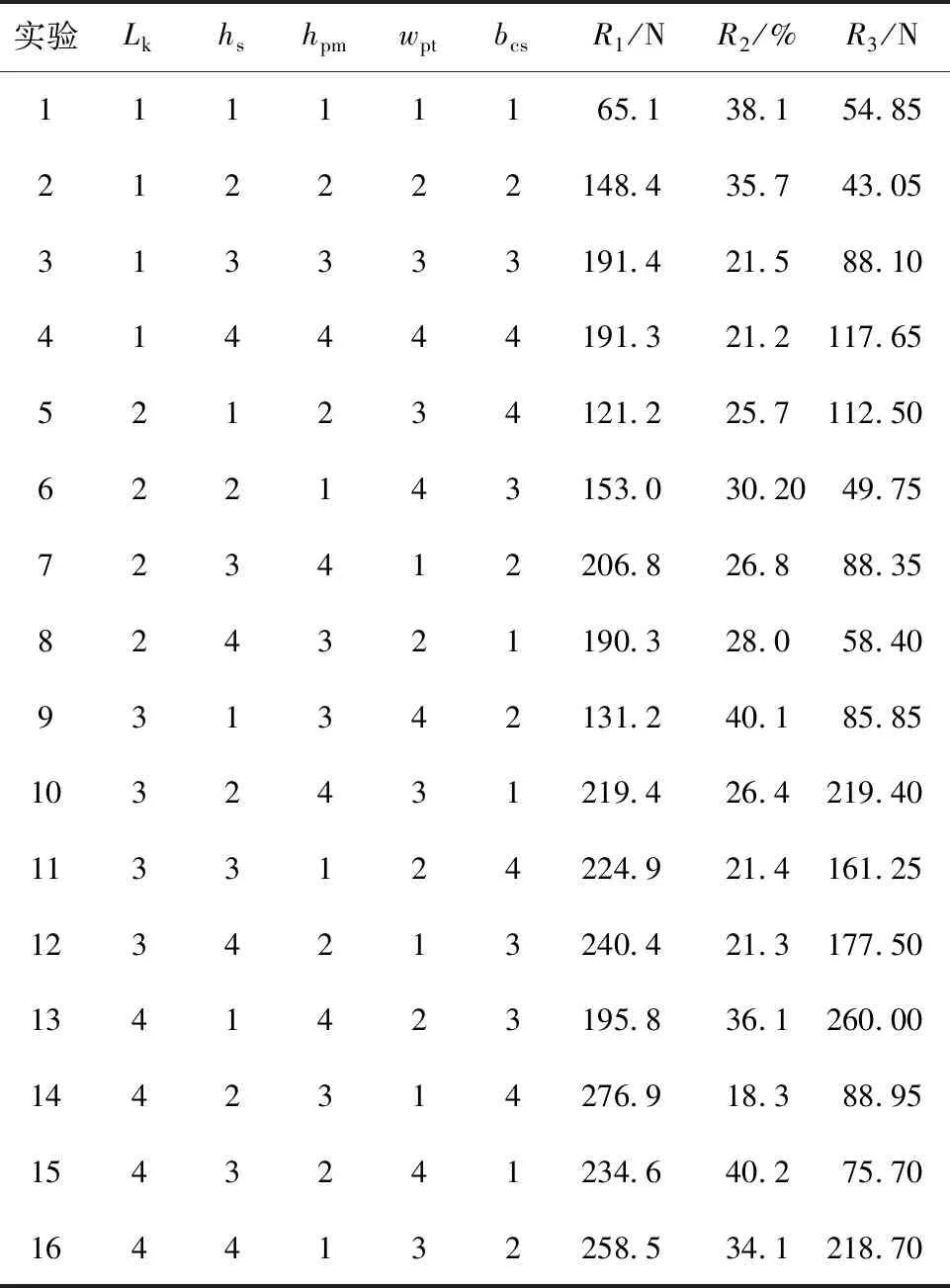
表4 田口法实验表与实验结果
通过比较不同因素的方差比重和灵敏度均值,明确了5个优化因素对优化目标的影响程度,如表5所示。由表5可得,推力主要受电机叠厚和次级槽宽的影响,推力波动主要受次级槽宽和次级高度的影响,法向力波动主要和电机叠厚、永磁体厚度和次级高度有关,故后续优化中仍考虑这5个因素的影响。

表5 分析结果
3.2 响应面法
响应面法可分为BBD、CCD、One Factor Design等,其中BBD适合5个变量以下的优化设计,为限制参数范围,避免出现错误的参数组合,本文采用CCD法,此外CCD具有近似旋转性和无序惯性特点,可以优先选择CCD。响应面CCD参数因子取值范围如表6所示,构造CCD实验进行有限元仿真,实验结果如表7所示。
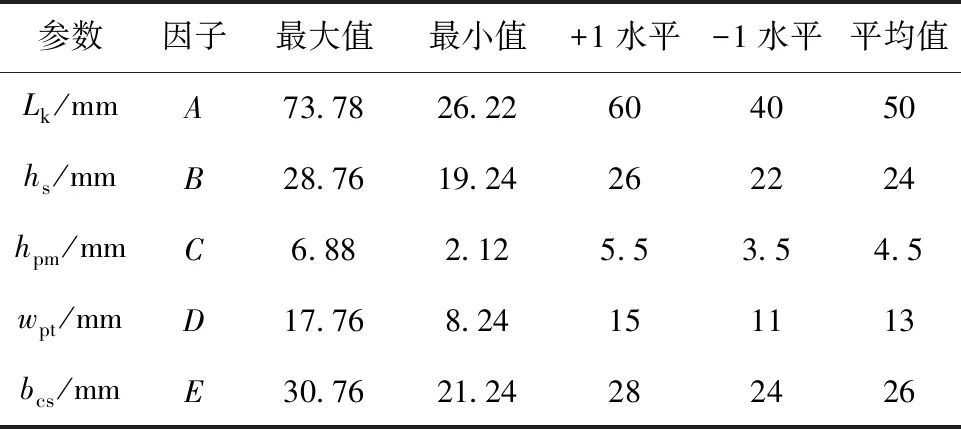
表6 CCD参数因子取值范围
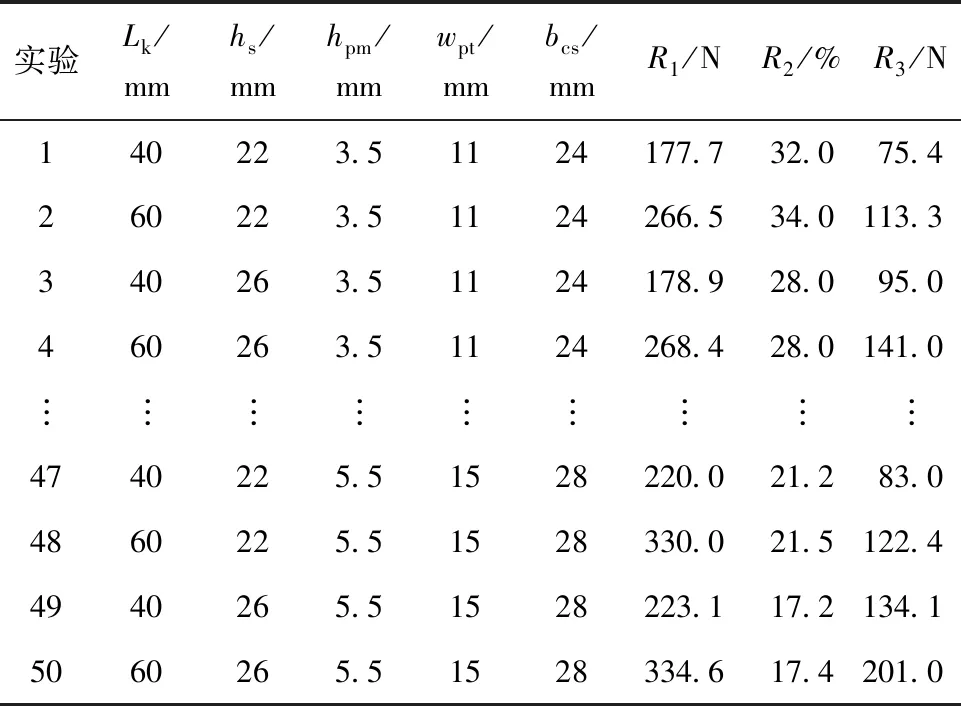
表7 CCD实验设计与结果
对实验结果构建拟合方程,如下式:
R1=251.75+50.45A+1.37B+20.94C-2.04D+14.51E+3.23AC+2.9AE-6.03CD+2.76CE+3.84C2-5.26E2
(10)
R2=19.73-1.27B-1.04C-0.808D-2.92E+1.09CD+1.22DE+1.59D2
(11)
R3=71.39+17.96A+2.65B+1.92C+3.96D+5.69E+8.28DE+24.35C2
(12)
为了判断以上拟合方程的正确性,设置评估条件如下:
(1)模型相关联的p值小于0.001,表示为显著;
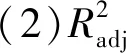
(3)精度k要大于4。
(13)
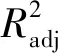
3.3 优化结果
对优化结果仿真分析,可得到多目标优化前与优化后参数对比,如表8所示,电磁力波形对比如图11所示。
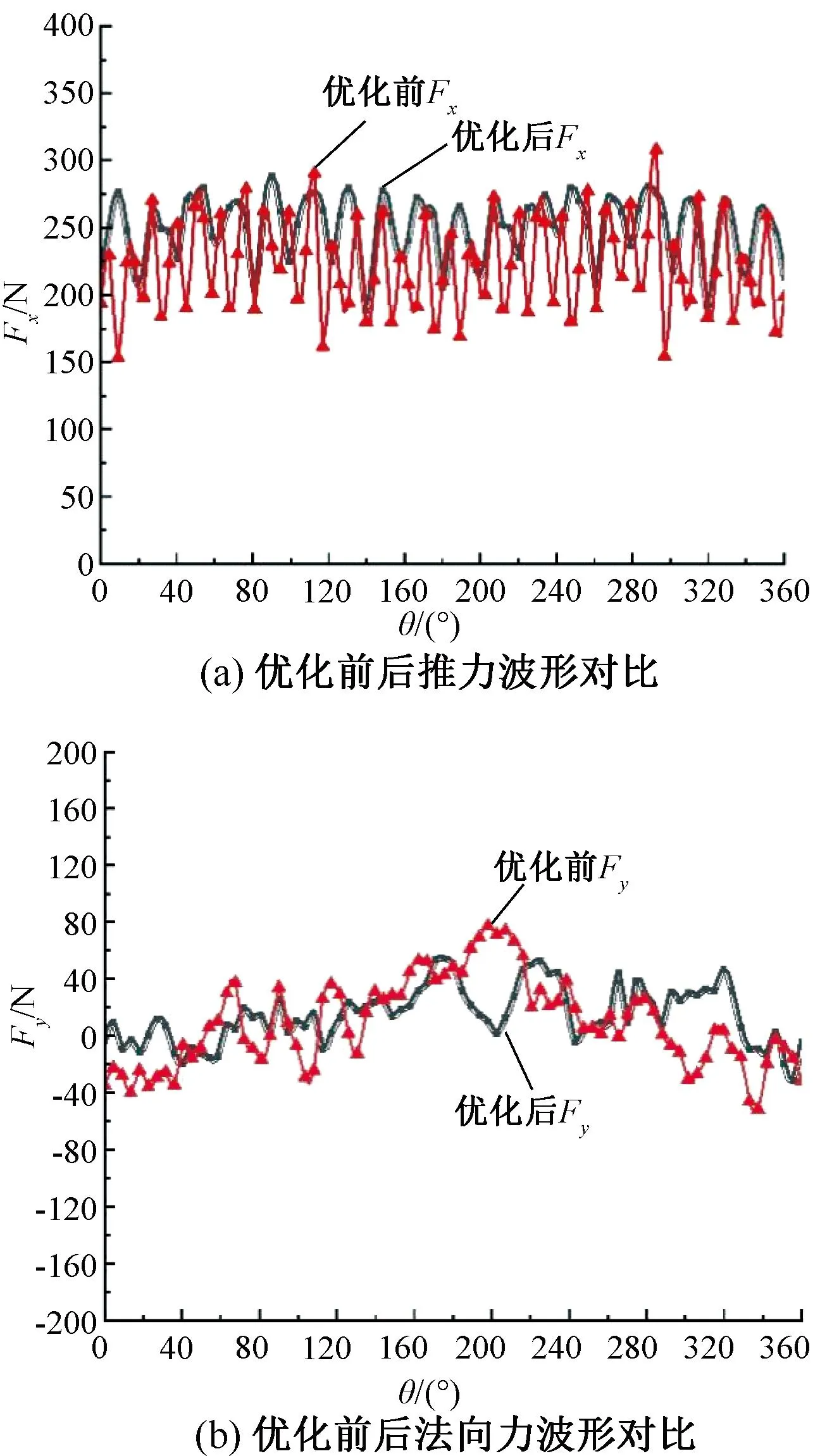
图11 优化前后电磁力波形对比
4 结 语
本文对一台6槽5极双边聚磁式槽口型PMLM展开了优化设计研究。首先分析了电机的工作原理,进行了单变量有限元分析,再在田口法基础上得到影响推力、推力波动、法向力波动峰值的关键参数,设计CCD组合实验,确定磁极厚度、初级齿宽、次级槽宽、电机叠厚、次级高度的实验表,以大推力、小推力波动和小法向力波动为目标进行优化,获得最优参数组合。优化结果表明,平均推力从223 N提升至235 N,推力波动从34%降低至18%,法向力波动峰值从64.7 N降低至44.4 N。

