永磁同步电机预测控制参数畸变影响分析

杨佳丽,沈艳霞,赵清元,谭永强

(1.江南大学 物联网工程学院,无锡 214122; 2.国网江苏省电力有限公司南京供电分公司,南京 210019)

0 引 言

永磁同步电机(以下简称PMSM)具有质量轻、体积小、功率密度高、可靠性强等优势,在电动汽车、航空航天、机器人、数控机床等伺服领域得到广泛应用[1-3]。在众多PMSM控制方法中,有限控制集模型预测电流控制(以下简称FCS-MPCC)因其对模型要求低、综合控制性能好、在线计算方便等特点脱颖而出[4-6]。该方法基于电机的离散参数模型,遵循代价函数取值最小原则,通过实时估算电流未来时刻值来给出逆变电路开关指令,无需空间矢量脉宽调制,即可实现快速控制电机转速的目的。

但PMSM是一个复杂的非线性、强耦合、多变量系统,其控制难度大、成本高[7-8]。FCS-MPCC在实际应用中仍存在明显的缺点:PMSM物理结构存在齿槽效应、边端效应和饱和效应,在运行过程中会出现温升参数变化,而预测结果依赖于系统模型参数,参数失配会导致控制性能下降[9]。为探索参数畸变影响实际转速的原因,提升FCS-MPCC的动、静态控制性能,进一步推广PMSM在伺服领域的发展与应用,针对参数畸变的影响分析具有重要意义。

本文针对参数畸变对于PMSM预测控制的影响进行了理论分析与实验探讨,为后续相关研究奠定基础。

1 PMSM预测控制工作原理

模型预测控制(以下简称MPC)作为一种现代控制理论,可以联合控制多个控制变量处理复杂的控制问题。为提高电机的控制性能和效率,满足不同的控制要求,MPC可分为:模型预测转矩控制[10-11]、模型预测通量控制[12]、模型预测电流控制(以下简称MPCC)。其中,MPCC以电流为控制目标,并在下一时刻使用电流和给定电流作为约束,以优化此时的最佳电压矢量输出,是本文探讨的对象。

1.1 PMSM数学模型

PMSM三相绕组电压由定子电阻电压和磁链感生电压构成,三相静止坐标系下的电压方程:

(1)

式中:ua,ub,uc为三相定子电压;ia,ib,ic为三相定子电流;ψa,ψb,ψc为三相绕组磁链;Rs为定子电阻。对式(1)进行Clarke、Park变换,可得在d-q旋转坐标系中的电压方程:

(2)

式中:ud,uq分别为d,q轴电压;id,iq分别为d,q轴电流;ψd,ψq分别为d,q轴绕组磁链;ωe为转子电角速度。三相静止坐标系下的磁链方程:

(3)

式中:ψa,ψb,ψc为三相定子绕组磁链;Laa,Lbb,Lcc为三相绕组自感;Mab,Mac,Mba,Mbc,Mca,Mcb为两两绕组间的互感;ψfa,ψfb,ψfc为永磁体磁场交链三相定子绕组的永磁磁链分量。对式(3)进行Clarke、Park变换,可得在d-q旋转坐标系中的磁链方程:

(4)

式中:Ld,Lq分别为d,q轴电感;ψf为永磁体磁链。将式(4)代入式(2)可得电压方程:

(5)

1.2 PMSM的MPCC原理

对d,q轴电流求导并离散化:

(6)

式中:T为控制系统采样时间;id(k),iq(k)为采样时刻的d,q轴电流;id(k+1),iq(k+1)为d,q轴预测电流。MPCC模型由PMSM电压方程推导而来,将式(6)代入式(5),经过推导可得MPCC模型:

(7)

基于该离散参数模型,MPCC通过实时估算电流未来时刻值来给出逆变电路开关指令,桥式逆变电路如图1所示。

图1 桥式逆变电路示意图

电路中,不同的开关状态会产生不同的三相定子电压,具体规则如下:

(8)

式中:Sw为逆变器三组开关的8种状态,分别为(000,001,010,011,100,101,110,111);i=1,2,3,4,5,6,7,8;udc为逆变器直流电压源。ua、ub、uc的变化会反映在d、q轴电压ud、uq中,即不同开关状态下,会有不同的d、q轴电压。将ud、uq代入式(7)中可计算d、q轴预测电流值,代价函数基于预测电流与参考电流之间的差值进行计算:

(9)

不同的开关状态下,代价函数取值也不同,最终输出使代价函数取得最小值的开关状态。桥式电路将根据开关指令为PMSM供电,从而实现对于电机转速的控制。

2 参数畸变影响分析

当PMSM的MPCC系统应用在实际工业控制过程中,电机参数由于温度、负载的变化以及外部干扰的存在常会发生畸变,具体包括定子电阻Rs、d轴电感Ld、q轴电感Lq以及永磁体磁链ψf。

令电机预测模型:

(10)

存在参数失配的实际模型:

(11)

(12)

式中:ΔR、ΔLd、ΔLq、Δψ为对应参数发生的畸变值,取值有正有负。由参数畸变引起的d,q轴电流增量偏差:

(13)

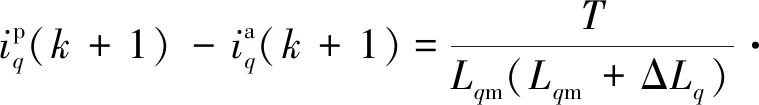
(14)

畸变的参数会引起预测电流发生偏差,此时,当把发生偏移后的预测电流代入式(9)进行计算,代价函数的取值也会随之发生偏移,进而改变逆变器电路开关状态选择,最终影响电机转速性能。

3 仿真搭建与实验

本节将对参数畸变的影响进行定性分析,为了探索参数畸变对于控制系统的定量影响,结合实验进行分析尤为重要。

3.1 仿真系统搭建

PMSM的MPCC系统框图如图2所示。控制系统采用双闭环控制结构,外环为转速环,内环为电流环,逆变器为中点钳位型桥式逆变器。外环依据转速反馈进行PI控制,得到电机q轴参考电流值;内环基于预测模型得到d,q轴预测电流值。不同的预测电流值会导致代价函数的取值不同,当代价函数取值最小时,输出对应逆变器开关状态,从而实现电机对于给定转速的跟踪。

图2 PMSM的MPCC系统控制框图

依照系统框图在MATLAB Simulink中搭建仿真,电机参数如表1所示,仿真框图如图3所示。

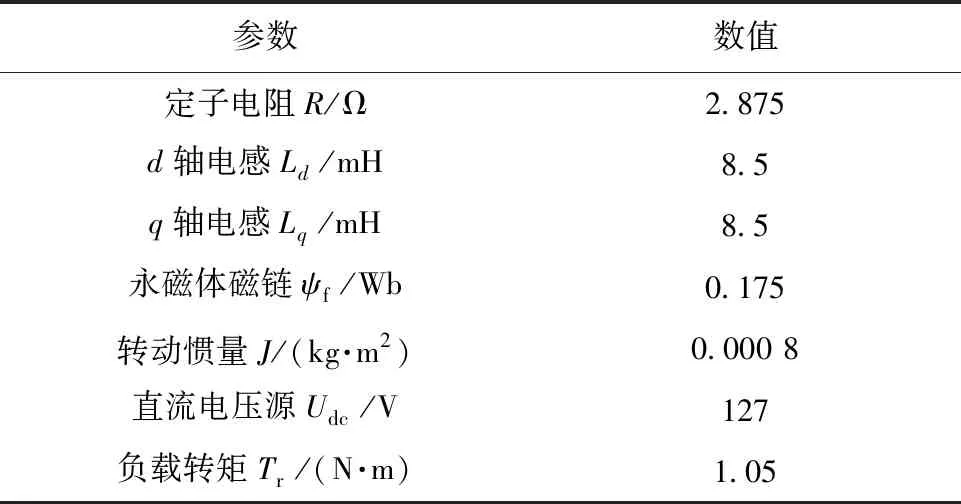
表1 PMSM仿真参数

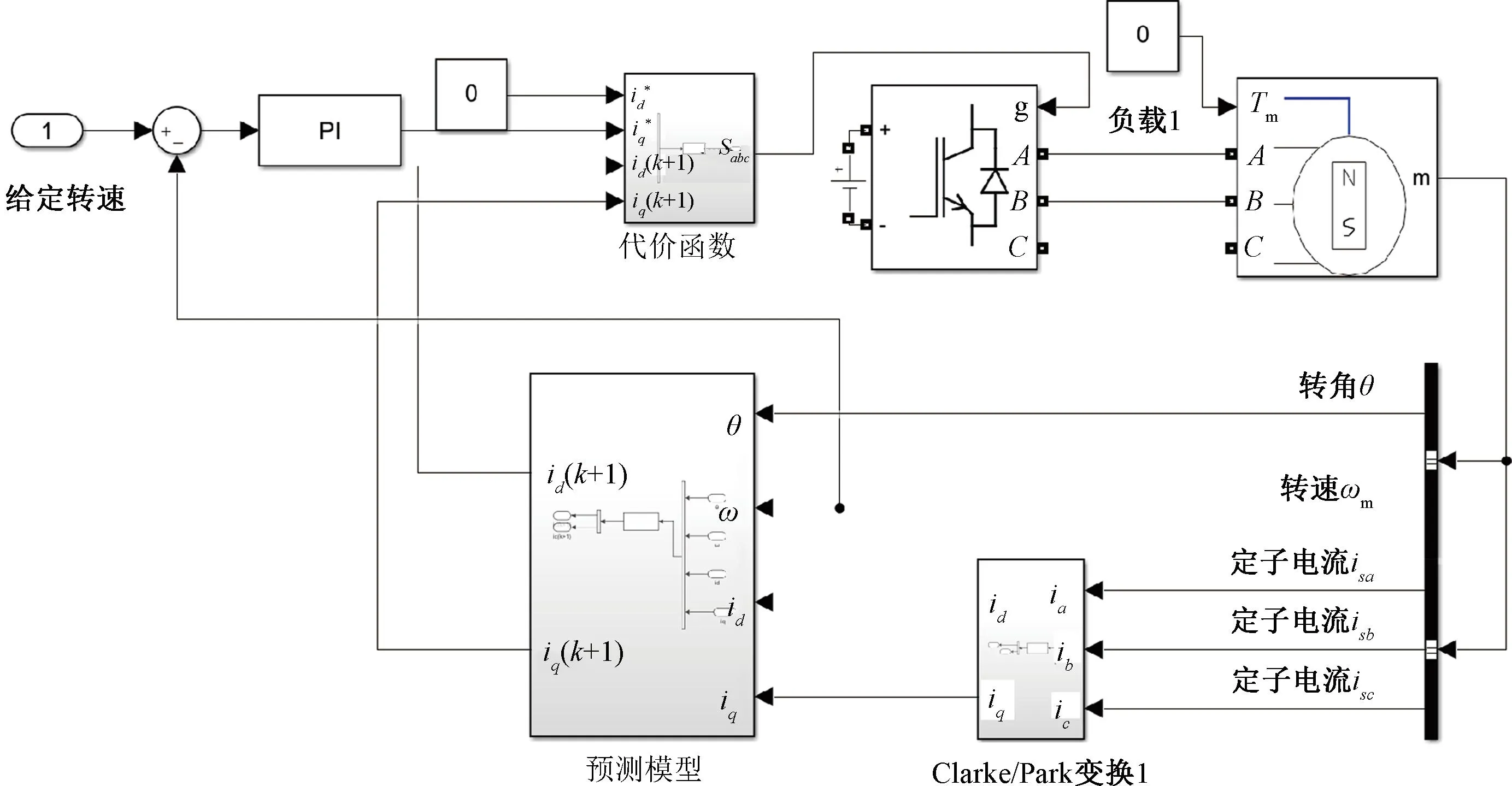
图3 PMSM的MPCC系统仿真图

3.2 实验设计与结果

为了模拟实际应用过程中电机参数的畸变,对电机仿真模型的参数R、Ld、Lq、ψf进行人为畸变。分别设置畸变范围-80%、-40%、+40%、+80%,测试各参数在不同程度畸变下对电机的影响。此外,设置了无参数失配的预测控制系统作为实验的对照组。

给定转速1 000 r/min,图4～图7分别为定子电阻R,定子电感Ld、Lq,永磁体磁链ψf发生畸变时电机响应曲线,具体包括d轴电流、q轴电流、电磁转矩Te、预测电流偏差Δid、Δiq以及转速曲线。

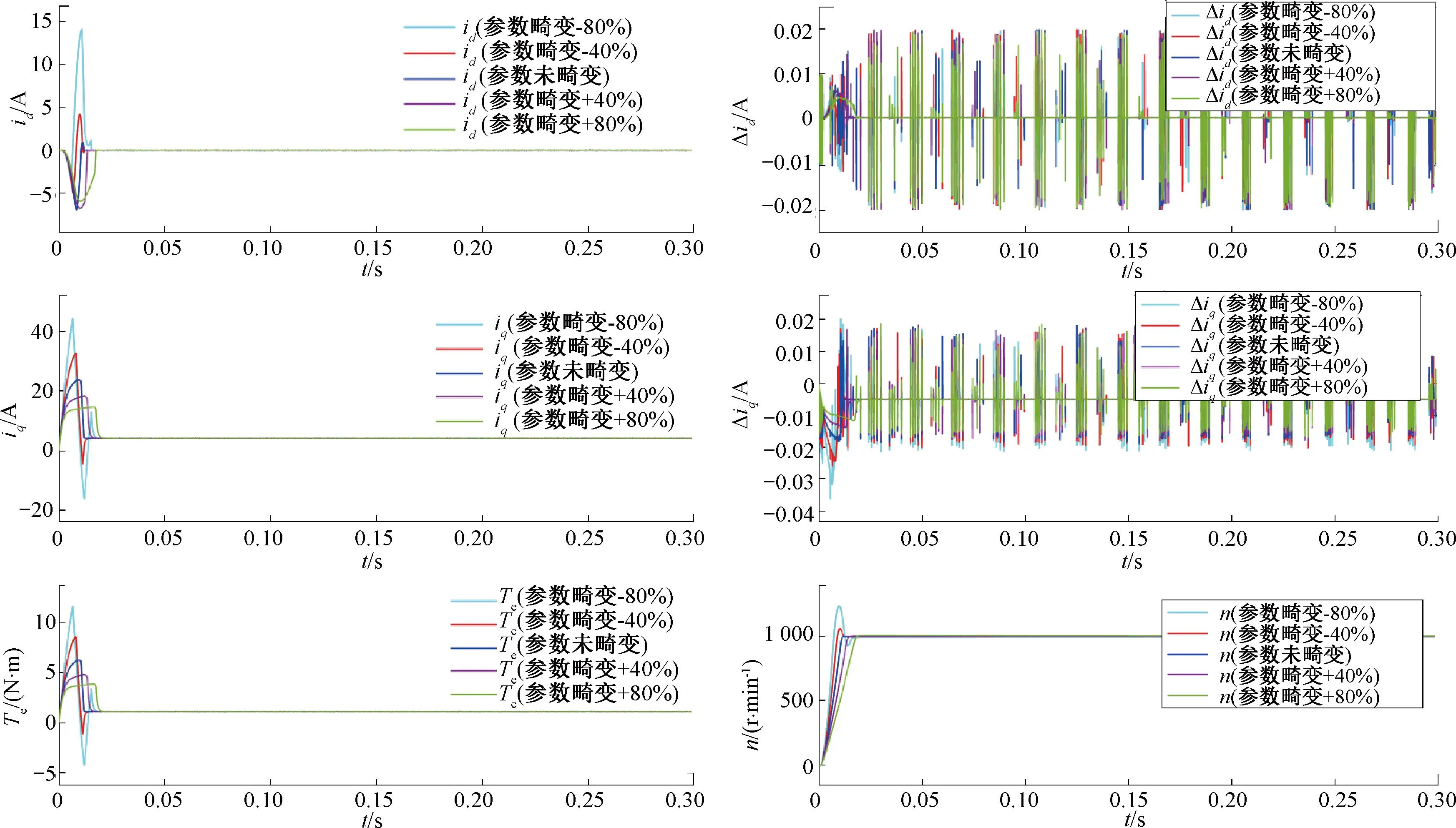
图4 参数R失配电机响应曲线图

图5 参数Ld失配电机响应曲线图

图6 参数Lq失配电机响应曲线图

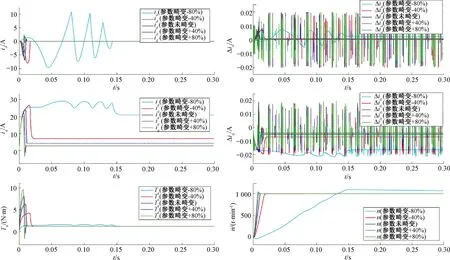
图7 参数ψf失配电机响应曲线图

由图4可知,当电阻发生负向畸变时,d、q轴电流以及电磁转矩在暂态过程中脉动幅值增大,转速发生超调,且稳态转速并未达到额定转速1 000 r/min,出现稳态偏差。随着负向畸变程度的加深,上述现象会进一步加深。当电阻发生正向畸变时,id、iq、Te在暂态过程中脉动幅值减小,但过渡到稳态所需时间变长;转速到达额定转速时间增加,最终稳态转速超过1 000 r/min,出现稳态偏差。随着正向畸变程度的加深,上述现象同样会进一步加深。Δid、Δiq并未发生明显改变,Δid维持在-0.02～0.02 A左右;Δiq维持在-0.03～0.02 A左右,电阻畸变对预测电流的影响较小。

当定子电感Ld发生畸变时,id、iq、Te在暂态过程中脉动幅值会随着畸变程度的变化而改变,具体变化规则与R发生畸变情况一致。在稳态情况下,随着Ld负向畸变程度的加深,id、iq、Te曲线的脉动增加。当Ld减小80%时,id脉动由原来0.06 A上升为0.3 A,iq脉动从0.04 A上升为0.065 A,Te脉动从0.01 N·m上升为0.025 N·m,转速未能达到额定转速,且随着负向畸变程度的进一步加深,转速出现小幅振荡,Δid明显增加,由-0.02～0.02 A上升为-0.1～0.1 A。当Ld正向畸变时,id稳态曲线脉动减小,iq、Te稳态曲线脉动无明显变化,稳态转速超过额定转速,Δid减小。在整个畸变过程中,Δiq无明显变化,始终维持在-0.02～0.02 A左右。Ld畸变对d轴预测电流影响明显,对q轴预测电流影响较小。

定子电感Lq发生畸变时,电机响应暂态过程中,Lq负向畸变,iq曲线脉动幅度增加,Lq正向畸变,id、Te曲线脉动幅度增加,iq曲线脉动幅度减小。在稳态情况下,随着Lq负向畸变程度的加深,iq、Te曲线脉动增加,iq脉动由原来0.05 A上升为0.3 A,Te脉动从0.013 N·m上升为0.08 N·m,id曲线无明显变化,维持在-0.03～0.03 A左右,转速未能达到给定转速,出现稳态偏差,Δiq明显增加。当Lq减小80%时,Δiq由-0.015～0.015 A上升为-0.07～0.10 A。当Lq正向畸变时,iq、Te曲线脉动减小,id曲线无明显变化,转速出现超调,且稳态转速高于额定转速,Δiq减小,Δid无明显变化,始终维持在-0.02～0.02 A左右。Lq畸变对q轴预测电流影响明显,对d轴预测电流影响较小。

当永磁体磁链ψf发生畸变时,随着ψf减小,id、iq曲线暂态过程脉动幅度增加,Te曲线暂态过程脉动幅度减小,三者到达稳态所需时间均增加;随着ψf增加,id、Te曲线暂态过程脉动幅度增加,iq脉动幅度减小,到达稳态所需时间均减小。在稳态情况下,随着ψf负向畸变的程度加深,iq稳态值增大,Te曲线脉动减小,转速响应时间增加,且未能达到给定转速,Δiq脉动幅度未变,但脉动中心由原来-0.005 A下降为-0.007 A。当ψf减小80%时,id、iq、Te曲线出现大幅脉动,转速性能大幅下降,Δid脉动幅度减小,Δiq脉动中心进一步下降为-0.016 A。当ψf正向畸变时,随着ψf逐渐增大,id曲线无明显变化,iq稳态值减小;Te曲线脉动增加,从0.012 N·m上升为0.02 N·m;转速出现超调现象,稳态转速超过额定转速,出现稳态偏差;Δiq脉动幅度未变,但脉动中心由原来-0.005 A上升为-0.003 7 A。ψf畸变对d轴预测电流影响较小,对q轴预测电流影响明显,随着畸变程度的加深,q轴预测电流偏差增大。

4 结 语

本文针对参数畸变对于电机MPCC系统性能的影响,从理论和仿真实验两个角度进行分析,基于MPCC模型,推导包含畸变量的d、q轴预测电流公式,理论层面上梳理了参数畸变发生影响的过程。设置参数畸变范围-80%、-40%、0、+40%、+80%,对参数R、Ld、Lq、ψf分别进行不同程度畸变,实验结果表明:

1)d、q轴电感Ld、Lq对预测电流影响明显,其次为永磁体磁链ψf,定子电阻R对于预测电流的影响最小,符合对式(13)、式(14)的理论分析。

2)即使d、q轴预测电流偏差保持在无参数失配水平,d轴电流、q轴电流、电磁转矩、转速仍会发生较大畸变。在电阻发生失配情况下,单纯通过参数补偿来减小预测电流偏差的方法无效,无法改善参数失配引起的电流、转矩脉动问题,转速动静态性能无法提升。

3)4种参数畸变均会使得d轴电流、q轴电流、电磁转矩出现脉动幅度增加的问题,但对转速的影响各不相同。R畸变影响转速的快速性、稳定性、准确性;Ld畸变影响主要体现在转速的准确性方面;Lq畸变对转速的影响突出体现在稳定性和准确性上;ψf畸变在快速性、稳定性、准确性方面均有影响。

仿真实验分析,定量体现了各参数对于控制系统的影响方式与程度。本文为后续相关参数研究奠定基础,针对高、中、低转速领域的参数畸变影响是下一步研究的主要内容。