考虑多运输模式的农村快递共配LRP问题
张文艺
(西南交通大学 交通运输与物流学院,四川 成都 610031)
0 引言
当前,在农村电商快递发展和“快递进村”工程加速落实双重助推下,农村快递市场已初具规模。截止2022年9月我国已建成各类农村快递服务站点26.7万个,实现98%的乡镇快递网点覆盖和90%的建制村快递服务覆盖,快递直投到村比例超50%,平均每天有一亿件包裹进出农村。但受农村地区幅员辽阔、居民居住分散、地形复杂、需求量小等因素限制,农村快递配送成本高、效率低、服务差、网点选址难、运营模式单一等问题突出[1-3],亟待通过集约化的方式优化运营。共同配送作为整合优化资源的重要策略,具有良好的经济社会效应,能够有效缓解资源浪费,提高车辆配送率,减少运营支出等,是解决农村快递难题的有效手段。
不少学者对农村共配的模式展开了定性讨论。Tao Chu[4]、Cheng Lin,等[5]提出了基于信息、设备、人力的资源共享配送模式;王永丽[6]提出了农村快递众包模式;赵广华[7]提出了基于第四方物流的农村电商共配模式;李洋[8]设计了依托公交的客货联运模式;江泽靓[9]提出了“农村物流+共享公交”“农村物流+共享人员”和“农村物流+共享家庭”三种共享模式。本文在已有研究成果的基础上,基于对加强快递业与邮政、交通、商贸流通等产业融合共配思想的认识和理解,提出基于县域的“1+N+N”农村快递共配模式,主要表现为:由邮政或一家有实力的快递企业牵头,号召多家快递企业建立共配联盟,整合县域快递业务和配送资源,共同建设县-乡-村三级物流寄递体系,并由联盟主体负责统筹安排以满足区域内寄递需要;与此同时,实现跨行业共配,与县域内客运公司、商贸流通企业建立合作关系,或利用农村居民闲置车辆,通过委托代理的方式完成货物运输。
为了实现共配策略,需要建立对应的共配网络并完善运营管理机制。本文聚焦农村共配网络优化,对物流网络中节点的选址和车辆路径安排展开讨论。近年来,对LRP问题的研究多集中在多层级、考虑同时取送货、多车型、时间窗等复杂约束的问题优化或算法改进上。Zhuo Dai,等[10]针对三级、四级LRP问题提出了一种基于改进Clarke和Wright节约算法的两阶段算法;李珍萍,等[11]探讨了多层级、多中心、多车型的城市共配网络优化问题,并设计自适应大邻域搜索算法求解;任腾,等[12]对城市个人客户和电商客户共同配送问题展开研究,并引入插入算法优化遗传模型对考虑同时取送货的路径问题进行求解;孙青伟,等[13]改进了遗传算法来求解同时取送货的选址-多车型路径问题;刘东,等[14]设计了混合免疫遗传算法来求解多成本指标下的同时取送货选址-路径模型;冷龙龙,等[15]加入了碳排放指标,讨论了考虑同时取送货的低碳选址-路径问题;张帆帆[16]构造了考虑同时取送货和带软时间窗的城乡共配三级四层网络,并设计双层规划模型对其进行求解。基于LRP研究基础,本文将结合县域共配体系结构,从运输模式上丰富LRP问题研究设定,构建考虑多运输模式的2E-LRPSPD模型并设计算法进行求解。
1 问题描述和模型建立
1.1 问题描述
本文研究的考虑多运输模式的农村快递共同配送LRP问题是指:在某农村区域内,快递共配联盟建设有县-乡-村三级物流寄递网络,包括一个县级共配中心、若干个乡镇级配送网点和村级服务站点。在考虑共配联盟自有车辆运输和委托代理运输两种运营模式下,设计联盟自有车辆循环取货、定点定线的客货联运班列运输和社会车辆捎带开环运输三种模式,考虑多车型,在满足客户需求的前提下,以成本最低为目标,求解乡镇级配送网点的选址问题、各下级节点车辆运输服务模式的选择及车辆行驶路径规划问题。
1.2 问题分析
(1)运输模式分析
①联盟自有车辆循环取货运输模式。该模式是基于联盟自有或可自由调度的车辆资源提出。在该模式下,联盟根据运输需要对车辆进行调度并采用循环取货模式实现快递寄递。具体表现为车辆从上级某节点出发后,依次访问该车所负责的下级节点并同时完成取送货业务,最终返回原上级节点,形成单向流通闭环回路。如图1所示,有3辆车分别按1-2-3-4-1、1-5-6-1、1-7-1的路径完成取送货业务。
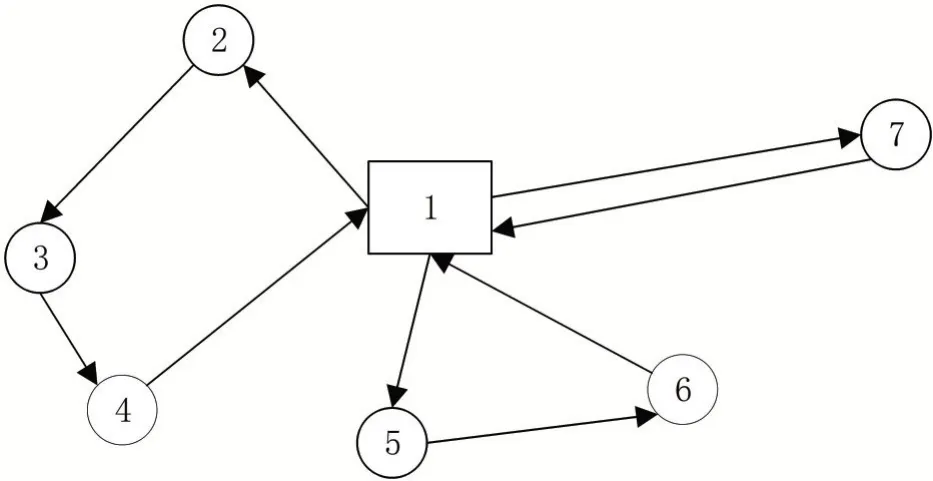
图1 循环取货模式示意图
②定点定线的客货联运班列运输模式。该模式是基于农村较为完备的客运网络和闲置的客运资源提出。在该模式下,联盟将快递委托给客运公司进行运输,以客运网络为基础,实现客货同网。该模式最大的特点是车辆线路既定,即已存在的客运班列,车辆按既定路线单向送货或单向取货,节点间形成双向串联通路。如图2所示,既定班列路线包括1-2-3,1-6-5-4,1-7,有3辆车分别按1-2-3、1-6-5-4、1-7的路径完成送货,有3辆车分别按3-2-1、4-5-6-1、7-1的路径完成取货。
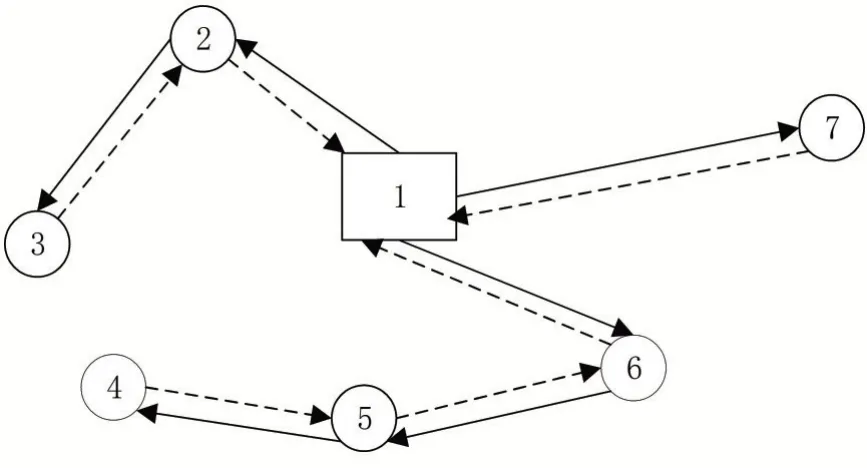
图2 往返取货模式示意图
③社会闲散车辆捎带开环运输模式。该模式基于社会闲散运输资源提出,如农村居民或小商户闲散车辆。在该模式下,联盟通过众包平台发布货物运输需求,闲散车辆通过平台接受订单并到指定地点取货进行单向捎带运输,实现快递寄递。该模式的特点表现为取送业务分离且车辆路径呈开环运输,即单一车辆只负责送货或取货并且不用回到起始点。如图3所示,有4辆车分别按1-2-3、1-4、1-6-5、1-7的路径完成送货,有4辆车分别按2-1、3-4-1、5-6-1、7-1的路径完成取货。
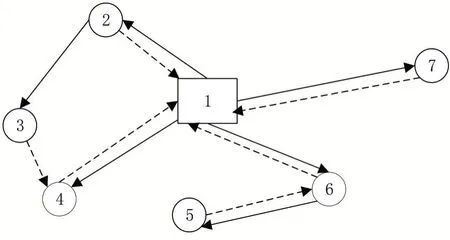
图3 捎带运输模式示意图
(2)车型分析。基于上述三种运输模式的特点,结合县-乡-村各层节点运输需求规模,本文设定有5种车型,运力较大的循环取货车和班列运输车用于县-乡层级的大规模一级配送,运力较小的循环取货车、班列运输车和捎带运输车用于乡-村层级的小规模二级配送。
1.3 问题假设
(1)各级物流网络节点位置信息已知。
(2)备选乡镇级配送网点对应的建设成本已知。
(3)客户寄递需求量已知。
(4)取货或送货业务不可拆分,且必须满足所有客户的需求。
(5)不考虑节点的处理能力或容量约束问题。
(6)货物均可以混装,不考虑货物运输条件的多样性。
(7)车辆运输能力约束仅考虑载重量和行驶里程。
(8)每辆车最多只能安排一条运输路径。
(9)车辆基本参数信息已知,不考虑同类型车辆间基本参数的差异性。
(10)不考虑跨级直接运输。
1.4 参数设置
(1)决策变量
(2)其他参数。G表示县级共配中心,标号为1;C表示备选乡镇级配送网点集合,标号为{2,3,…,c+1} ;ci表示第i个备选乡镇级配送网点;cod_ci表示备选乡镇级配送网点ci的建设成本;D表示村级服务站点即客户点集合,标号为{c+2,c+3,…,c+t+1} ;dj表示客户j,j∈{c+2,c+3,…,c+t+1} ;N表示物流网络节点集合,N=G ⋃C ⋃D;distij表示节点i到节点j的距离,i,j∈N;V表示车辆集合,V=V1⋃V2⋃V3⋃V4⋃V5;Vk表示第k种类型的车辆集合,k∈{1,2,3,4,5} ;vks表示第s辆k类型的车,s∈Vk;Qk表示第k种类型的车辆最大载重量;Mk表示第k种类型的车辆最大行驶里程;VFk表示第k种类型的车辆固定使用成本;VZk表示第k种类型的车辆在捎带运输模式下单位产品单位距离运输成本;VWk表示第k种类型的车辆在班列运输模式下单位产品运输成本;qijks表示k型车辆s在有向路段(i,j)上的载重量;e0ks表示k型车辆s在空载时的单位距离运输成本;e1ks表示k型车辆s在满载时的单位距离运输成本;dd1j表示客户j在上一寄递周期内的取货需求,j∈{c+2,c+3,…,c+t+1} ;dd2j表示客户j在本寄递周期内的取货需求,j∈{c+2,c+3,…,c+t+1} ;dd3j表示客户j在本寄递周期内的送货需求,j∈{c+2,c+3,…,c+t+1} ;dem_ddj表示客户j寄递需求,dem_ddj={dd1j,dd2j,dd3j} ;R表示节点i和节点j在班列运输模式下的路径连接情况矩阵,矩阵元素rij∈{0,1},i,j ∈N,其中rii=0,∀i ∈N,且rij=rji,∀i,j ∈N。rij=1表示节点i和节点j存在直接连接的班列运输路线,否则节点i和节点j间不存在直接连接的班列运输路线。
1.5 模型构建
以乡镇级配送网点建设成本和车辆运输成本之和最小为系统优化目标,建立考虑多种运输方式的农村快递共配目标优化模型:
其中:f1表示乡镇级配送网点建设成本。
f2和f4分别表示循环取货模式下车型1和车型3的运输成本,成本构成包括车辆固定使用成本和考虑车辆行驶距离和载重量的变动成本,并以来表示车辆在载重率下的单位距离油耗成本。
f3和f5分别表示班列往返取货模式下车型2和车型4的运输成本,引入单位产品委托代运费用来表示。
f6表示捎带运输模式下车型5的运输成本,引入单位产品单位距离委托代运费用来表示。
为满足节点取送货服务需求、车辆行驶里程与载重量约束以及物流网络流量守恒定律,创建约束条件:
式(8)-式(10)表示每个下级节点有且仅有一辆车负责取货或送货;式(12)、式(13)表示选择循环取货模式的节点同时实现取送货;式(14)、式(15)表示选择班列运输或捎带运输的节点取货或送货由不同的车辆分开实现;式(16)表示任意节点内部不形成车辆子回路;式(17)表示任意车辆最多只经过任意节点一次;式(18)、式(19)表示在县-乡层级和乡-村层级中各级下层节点间不形成子回路;式(20)、式(21)表示采用循环取货模式的车辆从下级某节点驶入后必须从该节点驶出;式(22)、式(23)表示采用循环取货模式的车辆必须回到起始点;式(24)、式(25)表示采用班列运输模式的车辆路径必须与客运线路一致;式(26)表示在乡-村层级中任意两个乡都不在一条路径上;式(27)-式(30)表示采用班列运输或捎带运输的车辆只能负责送货或取货;式(31)-式(34)表示采用班列运输或捎带运输的送货车辆必须从某一上级节点驶出并且不返回起点;式(35)-式(38)表示采用班列运输或捎带运输的取货车辆必须从下级某一节点驶出并最终回到上级节点;式(39)-式(44)表示车辆载重量约束;式(45)-式(46)表示车辆行驶里程约束;式(47)-式(52)表示物流网络中各节点流量守恒;式(53)-式(57)表示只有启动了的乡级配送中心才提供服务。
2 算法设计
遗传算法是根据大自然生物体进化规律而设计提出的一种启发式算法,能够求解优化复杂问题的全局最优解,具有可拓展性、良好的搜索能力和较强的鲁棒性,运用较为广泛。本文研究的考虑多运输模式的农村快递共配问题较为复杂,对求解算法的要求较高。因此,本文选用遗传算法为基本求解算法,根据问题研究需要和算法思路,对遗传算法的编码解码、选择、交叉、变异四大要点进行设计并说明。
2.1 编码与解码设计
基于研究问题的特殊性和求解需要,在此次研究设计的遗传算法中,本文设定了5 层实数编码(如图4所示),其中第一层表示每一个备选乡镇级网点是否被选中,对应的基因数量为备选乡镇级配送网点的个数c,取值表现为0或1,分别表示没被选中和被选中;第二层表示每个村级服务站点选择的运输服务方式,对应的基因数量为需求客户t,取值表现为1或2或3,分别对应自有车辆运输、班列运输和捎带运输三种运输模式;第三层表示每个乡镇级配送网点选择的运输服务方式,对应的基因数量为备选乡镇级配送网点的个数c,取值为1或2,分别对应自有车辆运输和班列运输两种运输模式,前三层均为数值编码;第四层表示乡-村一级的末端节点服务方式选择的优先级顺序,对应的基因数量为末端客户节点数t;第五层表示县-乡一级的末端节点服务方式选择的优先级顺序,对应的基因数量为备选乡镇级配送网点的个数c,后两层为顺序编码。按照这样的编码方式通过随机函数产生初始群体。

图4 染色体编码图示
针对解码设计,大致思路为:首先访问染色体第一层编码,确定乡镇级配送网点的选址信息,然后依据就近原则将所有的村级服务站点分配给与其最接近的乡镇级网点,乡级的运输需求也随即可推断出来。然后针对县-乡层级,因本层级只涉及自有车辆运输和班列运输,所以分两步完成。第一步,先考虑班列运输,通过访问染色体第三层乡被服务的方式,初步确定选择班列运输的村,并结合第五层信息确定村的节点子顺序。按照村级节点子顺序,依次访问节点并通过班车路线约束和车辆载重约束来最终确定该节点是否采用班列运输,若符合要求则保留,若不符合则将该节点归入自有车辆运输方式,直至所有按班列运输的节点都访问完成。第二步,通过访问染色体第三层确定自有车辆运输节点,整合上一步中不符合班列运输的点,确定所有按自有车辆运输的节点编号,并访问第五层获取节点子顺序,通过载重和里程约束来确定最后的路径信息。针对乡-村层级,分别对每个乡及其归属村进行讨论。因本级涉及到三种运输方式,所以分三步完成,依次是考虑班列运输、捎带运输和自有车辆运输,解码思路同县-乡一级。
2.2 选择算子
选择算子是为后续种群迭代提供更优质的父代群体,本次研究选择的是能够实现较快、较好搜索全局的二元锦标赛选择法,其大致思路为在种群中随机选择两个个体(每个个体被选中的概率相同),比较两个个体的适应度值并将表现较好的个体保留,重复上述操作直至保留的个体数达到种群规模。
2.3 交叉变异算子
交叉算子服务于遗传算法中新个体的产生,服务于遗传算法实现全局搜索。变异算子服务于遗传算法中的种群多样性,同时其自身的局部搜索能力能够加速向最优解收敛。结合编码设计中各层的实数类型,本文选用模拟二进制交叉(SBX)和子路径交叉(SEX)两种交叉方式、高斯变异法和2-opt组合优化邻域搜索算子两种变异方式,分别服务于第一、二、三层的数值编码区和第四、五层的排列组合编码区。
2.4 算法步骤
基于上述描述,结合遗传算法的一般实现步骤,针对本次研究,设计的遗传算法具体步骤如下,相应的流程图如图5所示。
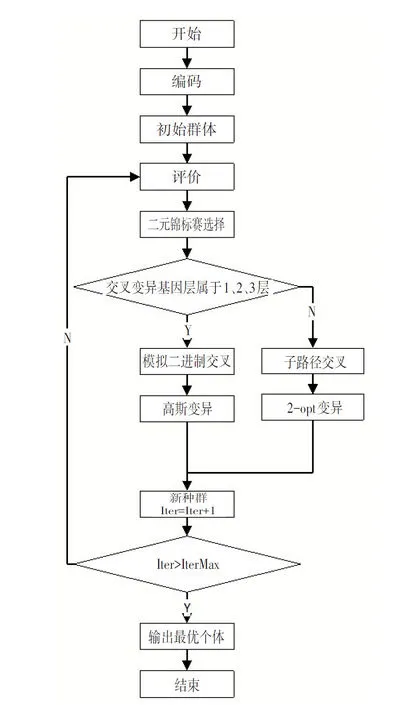
图5 求解算法流程图
Step1:设置参数:种群大小PopSize、最大迭代次数IterMax、交叉概率CrossProb、变异概率MutaProb;
Step2:基于编码机制随机生成初始群体,利用解码机制对每个个体进行解码并计算各个个体的适应度值,初始化迭代次数Iter=0;
Step3:根据二元锦标赛选择法,从父代种群中选出部分个体进行交叉变异操作;
Step4:依次访问染色体各层基因,判断是否发生交叉变异,若发生交叉变异,根据基因层级来选择模拟二进制交叉(SBX)或子路径交叉(SEX)执行交叉操作,采用高斯变异法或2-opt组合优化邻域搜索算法执行变异操作,最后形成新种群,完成一次迭代;
Step5:计算新种群中各个个体的适应度值,并找出该种群中最优的染色体,更新全局最优解;
Step6:更新迭代次数Iter=Iter+1;
Step7:如果迭代次数Iter大于最大迭代次数IterMax,则转到Step8;否则,转到Step3;
Step8:输出结果并结束算法。
3 实例模拟与结果分析
为了验证模型的可行性和正确性,利用随机函数生成1个县级共同配送中心(节点编号为1)、6个备选乡镇级配送网点(节点编号依次为2到7)、22个末端客户节点(节点编号依次为8到29)的节点坐标信息以及末端客户的需求信息。末端客户节点对应的坐标信息和需求信息见表1。
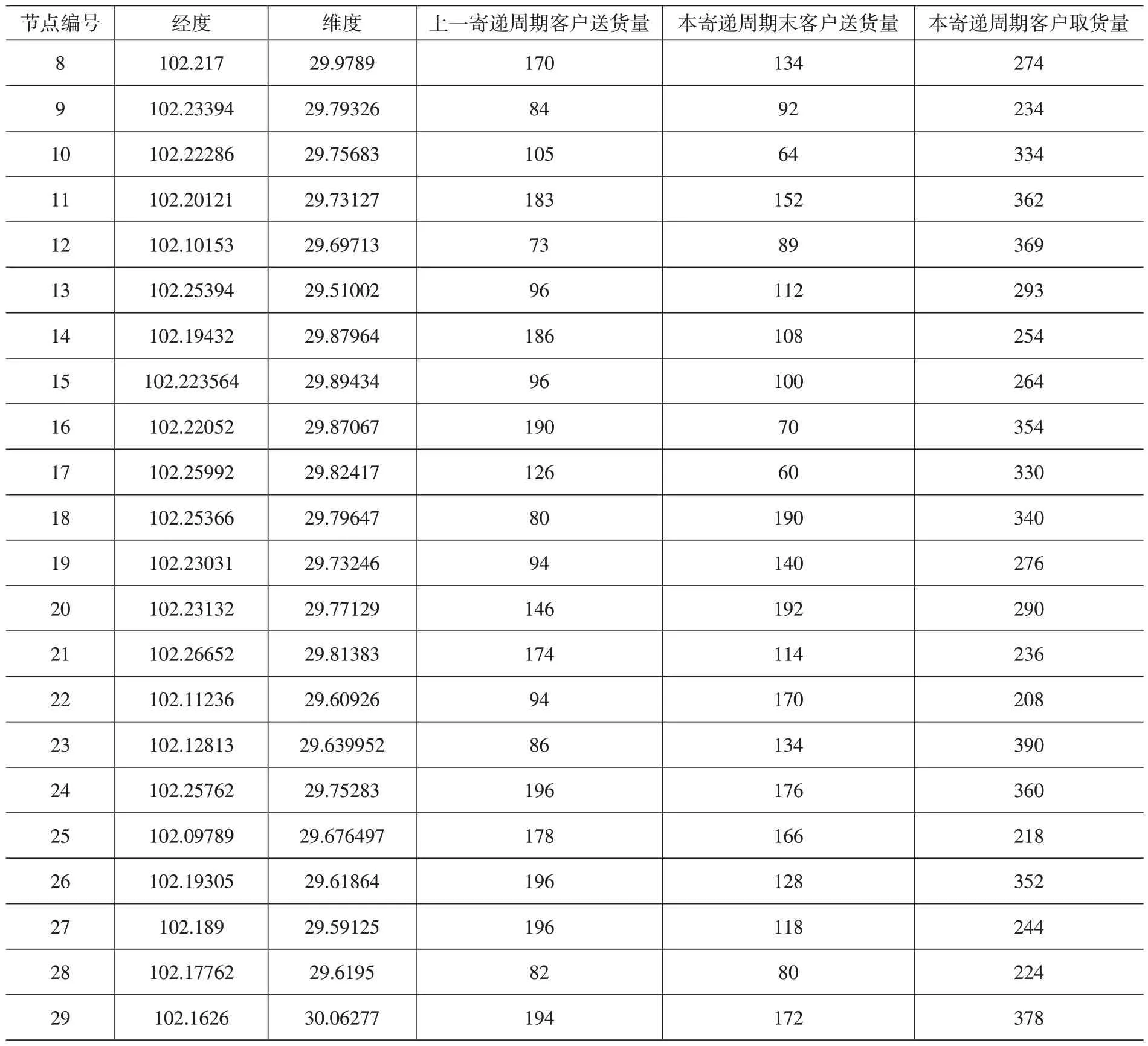
表1 村级服务站点位置及需求信息统计表
假设6个备选乡镇级配送网点对应的建设成本为18万、17万、15万、17万、19万和16万,整合节点位置信息,得到备选乡镇级节点信息,见表2。县级配送中心对应坐标为(102.23493,29.914206)。
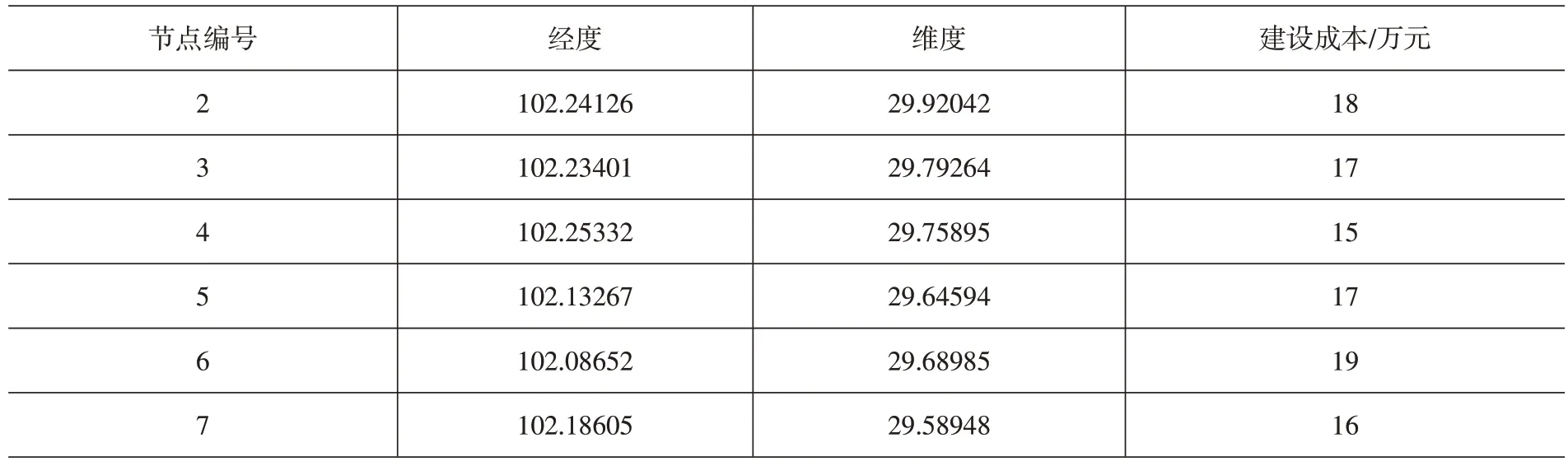
表2 乡镇级配送网点信息统计表
针对不同车型,设定车辆基本参数信息,见表3。
假设县-乡-村客运班列路线有1-2-4,1-3-5-6-7,2-14-16,3-15-8,3-9-18-17,4-20-21,4-19-10,5-11,5-23-22,6-25-12-24,7-27-26-13,7-28-29共计12条班列线。设置遗传算法参数,取最大种群数为100,最大迭代次数为500,交叉概率为0.6,变异概率为0.1,运行模型迭代过程如图6所示。得出结果如下:
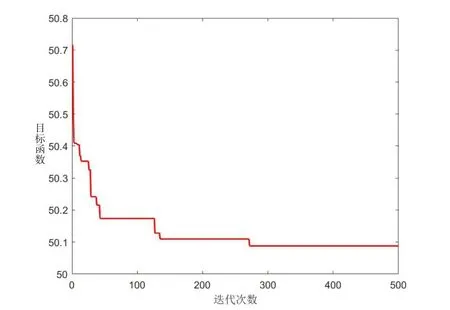
图6 模型求解迭代图
总成本共计50.087 8万元。其中乡镇级配送网点建设成本48万元,建设节点包括节点3、4、7,其中乡镇节点3服务村级节点8、9、14、15、16、17、18、20、21、29,乡镇节点4服务村级节点10、11、19、24,乡镇节点7服务村级节点12、13、22、23、25、26、27、28。
县-乡一级联盟自有车辆运输成本8 326.38元,车辆1负责节点3,共计送货2 954,取货1 446;车辆2负责节点7,共计送货2 298,取货1 001。
县-乡一级班列运输路线1-2-4运输车服务于节点4,运输成本1 910元,共计送货1 332,取货578。
乡-村一级联盟自有车辆运输成本8 715.96元,其中车辆1路线为3-15-14-29-16-21-3,共计送货1 486,取货564;车辆2路线为4-19-11-24-4,共计送货998,取货468;车辆3路线为7-28-23-25-12-22-7,共计送货1 409,取货639;车辆4路线为7-13-7,共计送货293,取货112。
乡-村一级班列运输成本为566元,班列3-15-8负责节点8,共计送货274,取货134;班列3-9-18-17负责节点9,共计送货234,取货92;班列4-19-10负责节点10,共计送货334,取货64。
乡-村一级捎带运输成本为1 359.68元,其中车辆1负责节点20的送货,送货量290;车辆2负责节点18的送货,送货量340;车辆3负责节点17的送货,送货量330;车辆4负责节点17、18的取货,取货量250;车辆5负责节点20的取货,取货量192;车辆6负责节点27的送货,送货量244;车辆7负责节点26的送货,送货量352;车辆8负责节点26、27的取货,取货量246。
4 结语
农村电商快速发展给农村物流带来发展机会的同时也暴露出农村物流发展的众多问题,为满足农村地区发展需要,实现乡村振兴,农村物流改革迫在眉睫。共同配送作为一种先进的资源优化配置方法,通过整合多方资源,能够有效缓解农村地区物流基础设施建设不足、运输效率差、运营成本高等难题,提高社会资源利用率,是打破农村物流发展困境的一种有效方式。本文针对农村快递发展,结合共配理论,设计了基于县域共配的“1+N+N”农村快递共配模式,丰富了农村共配模式类型,同时也为实业界开展农村共配提供了新思路。另外,针对共配模式,本文构建了多层级、多运输模式、考虑同时取送货的选址-路径问题优化模型,进一步完善了相关理论体系。
但本研究仍存在很多局限,比如考虑的是某一寄递周期内的静态需求,未考虑品种多样性以及运输条件的多样性,在目标追求上局限于节点的建设成本等,在未来的研究中还需继续突破。

