基于量子计算和威布尔分布的混合CHIO算法求解JSP 问题*

亓祥波 赵品威 王 润

（沈阳大学机械工程学院，辽宁 沈阳 110044）

在制造业中，作业车间调度问题（job-shop scheduling problem，JSP）被证明是一种极具挑战性的约束组合优化问题，也是一个典型的NP-hard 问题。这类问题的特点是，无法找到一种有效的算法在多项式时间内准确地求解其最优解[1]。它涉及如何合理地安排工作流程和资源分配，以最大化生产效率和利润。随着全球制造业的发展和竞争的加剧，对调度的优化变得越来越重要，设计科学合理的调度方案可以提高生产效率和经济效益，因此，对调度优化算法的研究成为调度领域研究热点之一。

近年来，受自然界各种生物群体行为、物理现象和自然现象等启发设计出来各种智能优化算法，因其具有较强的全局搜索能力、自适应性、鲁棒性、并行计算能力以及易实现等优点而被广泛应用于离散调度的问题求解中。刘丽娜等提出了一种改进麻雀算法（ISSA）[2]，通过引入高斯变异扰动、正余弦搜索等策略提高了麻雀算法对离散调度问题的求解精度。为了解决状态转移算法在过分依赖初值、局部搜索能力差、收敛速度慢等方面存在的不足，吴贝贝等提出了一种量子状态转移算法（QSTA）[3]，该算法引入了量子旋转门的思想，通过将最小化最大完工时间作为目标函数来解决离散调度问题，最后通过试验验证了该算法能够有效地求解离散调度问题。陈斌等提出了一种多策略引导的电磁场优化算法（MGEFO）[4]，该算法通过引入了自适应电磁移动系数，并采用不同的引导策略来动态调整粒子间的正电距离和负电距离，通过实验结果验证了该算法在解决离散调度问题方面的可行性。亓祥波等针对离散调度问题的特性提出了一种基于交叉选择的变邻域蜂群算法（VABC）[5]，增强了人工蜂群算法在离散调度问题上的搜索能力。

以上针对调度问题设计的改进算法在一定程度上取得了成果，为进一步研究提供了参考。然而，这些改进算法大多是对较为传统的优化算法的改良和设计，很少尝试使用新型智能优化算法进行对调度问题进行求解。冠状病毒群免疫优化算法[6]是2020 年Al-Betar M A 等提出的一种新的元启发式优化算法，灵感来源于造成世界性传播的新冠病毒，该算法模仿了群体免疫策略和社会距离概念，其基于3 种类型的个体病例用于群体免疫：易感、感染和免疫。每个易感人群与感染个体接触而感染病毒，再通过个体是否免疫而更新引导群体免疫以达到算法收敛。

针对CHIO 后期搜索能力差、收敛精度低等缺点，已有不少学者对其进行了改进并应用在不同实际问题上，例如路径规划[7]、医疗检测[8]和设计优化[9]等，但对于离散调度问题应用相对较少。本文以CHIO 为基础并对其进行了改进将其应用到车间调度问题上，与其他几种改进的优化算法进行了仿真对比实验，证明了算法在求解JSP 方面有较强的能力。最后，将提出算法应用到发动机生产调度实例上，进一步验证了所提出算法的可行性和优越性。

1 作业车间调度模型

1.1 JSP 问题的描述

JSP 问题可以理解为在具有特定工序的n个工件在m台机器上进行加工。每个工序的加工机器以及加工每道工序所需的时间都是已知的。调度的目标是安排每台机器上工件的加工顺序，根据排序确定每个工序的开始和结束时间，以实现最小的完工时间。JSP 问题满足以下假设：

①机器是独立的。

② 加工准备时间已被计入加工时间。

③所有机器从0 时刻开始可用。

④ 各工件加工的优先级相同，同一工件不同工序之间存在先后约束。

⑤ 每道工序在同一时刻只能由一台机器进行加工。

⑥ 加工过程中没有缺料或机器故障的情况。

1.2 作业车间调度的数学模型

本文使用整数规划模型[10]对JSP 进行描述，其模型如下：

其中：式（1）为最小化最大完工时间的目标函数；式（2）为工艺约束；式（3）为机器约束；cik为工件i在机器k上的完成时间；pik为工件i在机器k上的加工时间；M是一个充分大的正数；xihk是指示系数，xijk是指示变量，其含义为

1.3 基于工序的编码

选择恰当的编码规则对于获得优秀的调度方案至关重要，尤其是在表示JSP 的解时。本文采用基于工序的编码方式来实现这一目的。工序编码由工件号组成，编码的总长度等于任务的总加工工序数。在解码过程中，按照从左到右的顺序对工序编码进行安排加工。当一个工件号第一次出现时，表示该工件正在进行第一道工序的加工；当同一个工件号第二次出现时，表示该工件正在进行第二道工序的加工；以此类推，直到所有工序都被安排完成。以一个3×2 规模问题为例，具体见表1。

表1 编码对应规则

对离散变量除以机器总数向上取整，即得到基于工序的编码[1,3,3,2,1,2]。

2 量子混合CHIO

2.1 标准CHIO 算法

在CHIO 算法中，有3 种类型的个体病例：易感、感染和免疫。传播冠状病毒的速度取决于感染者如何与其他社会成员直接接触。群体免疫是当大多数群体具有免疫力时，群体达到的一种状态，这种状态可以防止疾病的传播。这些概念是根据优化概念建模的，既模仿群体免疫策略，又模仿社会距离概念。CHIO 对群体免疫策略进行了建模：在初始化种群HIP 后，随机产生与HIS一样多的一组病例（即个体）。生成的病例以二维矩阵n×HIS形式存储，且每个个体均对应一个状态向量Si和年龄向量Aj，HIP 为

式中：HIS为种群个数；n为问题维度。

在算法迭代过程中，xi病例的j基因要么保持不变，要么受到社会距离的影响，其影响根据基本繁殖率BRr，取值为0.05，见式（8）。

式中：r表示(0,1)的随机数；(t+1) 表示(t)更新后的基因值。

式中：r表示(0,1)的随机数；(t)表示从易感个体中选择的个体，此时m={i|Si=0}。

式中：r表示(0,1)的随机数；(t)表示从免疫个体中选择的最好的个体，此时v={i|Si=2}。

随后更新群体免疫群体，计算新个体xi(t+1)的免疫率（即适应度值），如果f(xi(t+1))>f(xi(t))，则xi(t+1) 取代xi(t)。且如果该个体为感染个体，则年龄向量Aj增加1。其中个体对应状态向量Si也随着适应度值改变，见式（12）。

式中：∆f(x) 表示当前种群的平均免疫率；is_Corona表示当前个体是否继承过感染个体基因。如果继承过感染个体的基因、当前个体为易感人群且免疫率小于平均免疫率，则该个体感染病毒，此时该个体的 Si=1；如果当前个体免疫率大于平均免疫率且当前个体为感染个体，则该个体为免疫个体，此时该个体的 Si=2。

最后，当个体年龄大于最大年龄后，该个体将重置：

式中：ub、lb分别表示问题的上下界；rand表示(0,1)的随机数。

2.2 QCHIO 算法

2.2.1 量子计算

由于CHIO 在求解JSP 时存在收敛精度低、寻优能力差等缺点，因此将量子计算[11]的思想引入到CHIO 算法。其中单量子比特的叠加状态为

在量子计算中，实现逻辑变换的基础是量子逻辑门。这些门操作主要用于改变量子态的性质。常见的几种量子门包括Hadamard 门、相位门和量子旋转门等。量子旋转门表达式为

量子旋转门的更新表达式如下：

在更新过程中对工序序列进行量子优化，则工序序列经过单链编码量子旋转门变换后表达式为

式中：Qxi表示xi通过量子计算产生的新个体。

2.2.2 威布尔分布变异

威布尔分布又称为韦伯分布、韦氏分布，是一种连续概率分布，一般用于工业制造、预测天气、可靠性和失效分析、量化寿险模型的重复索赔等。其概率密度函数（probability density function，PDF）为

式中：A为尺度参数，表示函数的走势；B为形状参数，表示函数的形状。图1 表示尺度为A、形状为B的威布尔分布的PDF。Sahoo S K 等[12]将威布尔分布算子应用到飞蛾扑火算法上证实了其可以当前位置搜索到有用的信息，因此将改进威布尔分布算子引入CHIO 以增加算法的多样性，通过改进威布尔分布算子的大步长和小步长来平衡算法的局部搜索和全局开发能力，以增强算法的收敛精度。具体实现见式（21）～式（23）。

图1 威布尔分布示意图

式中：S TEP表 示大步长，step表 示小步长，sign(rand-0.5) 表示随机取得的-1 或1 的向量，wbl(1,1)表示A、B均为1 时生成的威布尔分布的随机数，norm为范数函数，j表示个体的第j维，xi表示第i个个体，xbest表示当前种群中最优个体，xnew表示xi生成的新个体。

2.2.3 β-登山局部搜索

登山（hill climbing，HC）算法是一种简单的贪心邻域搜索算法。该算法每次从当前解的临近解空间中选择一个最优解作为当前解，直到达到一个局部最优解。但其主要缺点是易陷入局部最优解。为克服该缺点，Al-Betar M A 等提出了一种 β-登山算法[13]。在CHIO 中引入了 β-登山算子以平衡局部搜索和全局开发，从而提高CHIO 的收敛精度。具体实现见式（24）和式（25）。

式中：xj表 示当前个体的第j维，j是从当前个体 中随机选择的一个维度；r1表示(0,1)的随机数；表示一个常数，取值为0.001。

式 中：xi表示当前个体的第i维，lbj、ubj分别表示问题求解范围的下界和上界在第j维的位置，r2和R均表示(0,1)的随机数。最后采用贪婪选择，如新个体的适应度值大于原个体，则新个体取代原个体。

2.2.4 多邻域搜索

在优化算法中，邻域搜索是一种通过使用邻域函数来创建解的邻域，并在邻域中找到比当前解更优的解来进行替换的方法。在本文中，经过迭代过程后，对种群中的最优个体依次进行了交换、倒置和倒序操作。每次操作都会保留适应度值较优的个体，以增强算法的挖掘能力。

具体的多邻域搜索方法如下。

（1）交换操作：假设加工任务总加工工序数为N，在1～N中随机选择两个不同的位置，然后交换这两个位置的加工工序。

（2）倒置操作：假设加工任务总加工工序数为N，在1～N中随机选择一个位置Oa，然后将该位置与其后面的工序位置Oa+1进行交换。如果选择的位置是最后一个位置，则将该位置的工序与工序列表中的第1 个位置的工序进行交换。

（3）倒序操作：假设加工任务总加工工序数为N，在1～N中随机选择两个不同的整数为a和a+p，假设未进行倒序操作前的工序编码为O＝[O1,O2,O3,···,Oa,Oa＋p,···,ON]，则执行倒序操作后的序编码为Onew＝[O1,O2,···,Oa＋p,Oa+p-1,···,Oa,···,ON]。

2.3 QCHIO 算法的流程

QCHIO 的流程图如图2 所示。

图2 QCHIO 流程图

3 实验验证与结果分析

为了验证所提出算法QCHIO 的性能，采用了车间调度上典型的FT 算例与LA 算例进行仿真测试。实验PC 设备参数为：CPU 为AMD Ryzen7 5700U、主频为1.8 GHz、运行内存为16 GB、操作系统为Windows 11。编程环境为Matlab 2018b。

3.1 对比算法及参数设置

为了便于对比分析，选取了几种较为先进的算法作为对比算法，其中有改进麻雀算法（ISSA）[2]、量子状态转移算法（QSTA）[3]、多策略引导的电磁优化算法（MGEFO）[4]、标准CHIO[6]算法。为了验证改进策略的有效性，对算法进行了消融实验，见表2，其中ICHIO1、ICHIO2、ICHIO3、ICIO4 分别表示在QCHIO 的基础上无量子计算算子、无威布尔分布算子、无 β-登山算子、无多邻域搜索算子。为了便于对比，将实验参数均设置种群个数为50，最大迭代次数为500，算法独立运行30 次，记录其平均值（avg）、最优值（best）作为实验结果，结果见表3，QCHIO 相对于对比算法的改进提升水平见表4，同时选取了几个具有代表性的算例给出了平均迭代曲线和甘特图，如图3 和图4 所示。

图3 在部分算例上的平均迭代曲线

图4 在部分算例上的甘特图

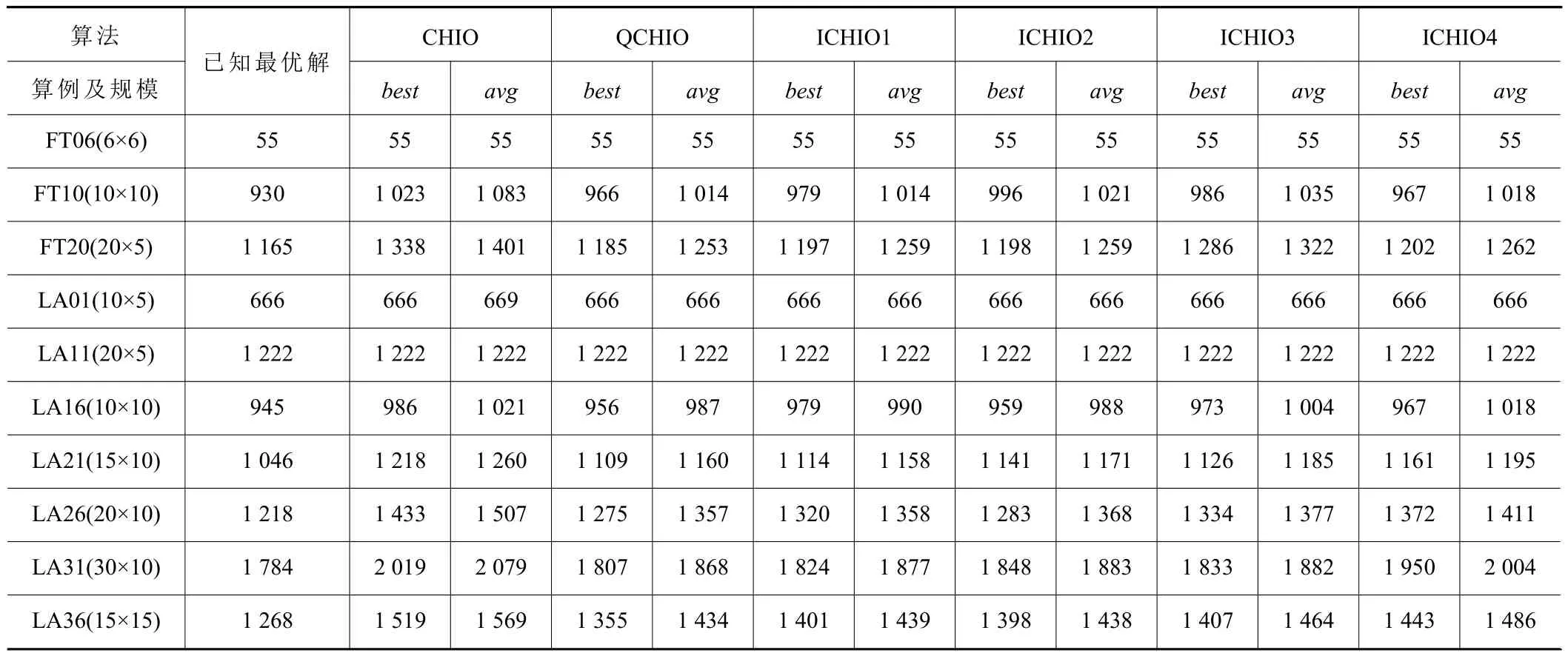
表2 消融实验结果

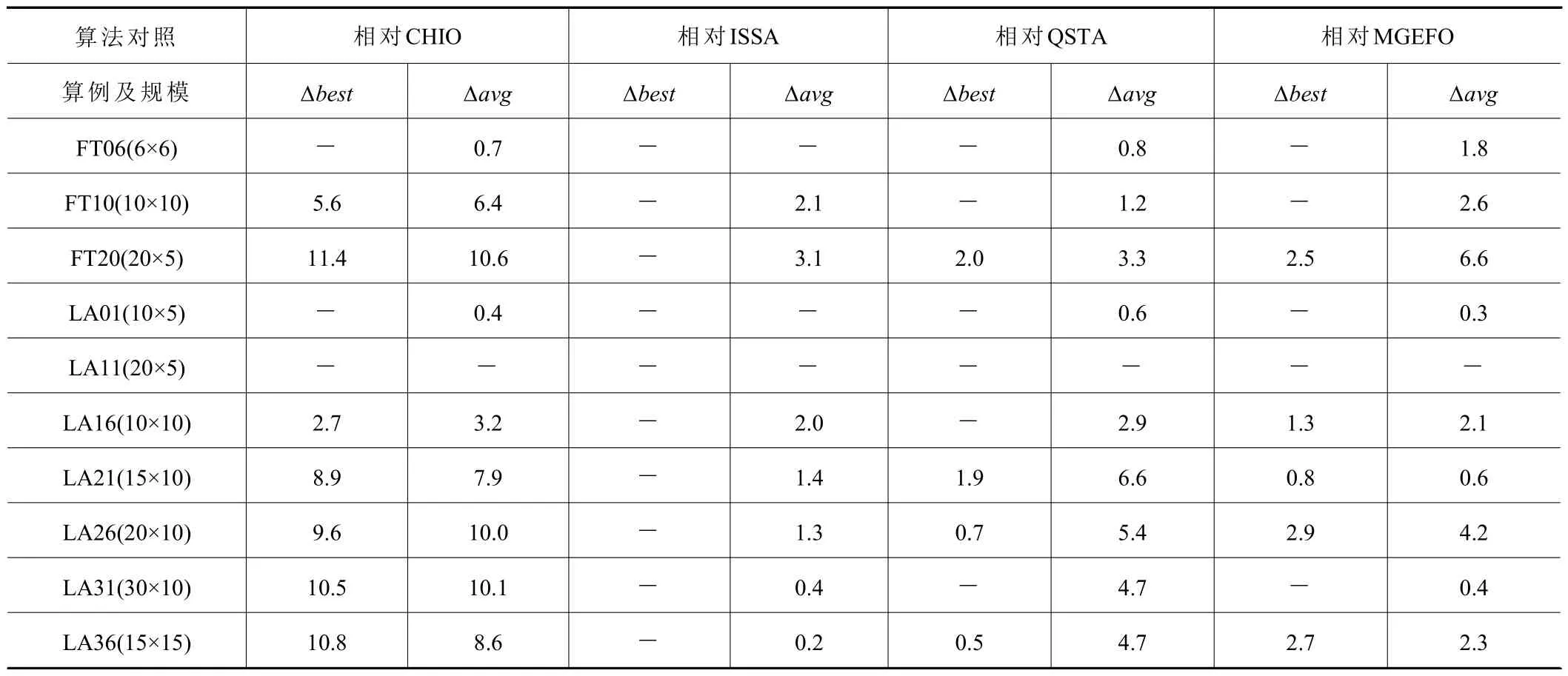
表3 QCHIO 与部分改进算法在算例上的对比（%）

表4 QCHIO 相对于CHIO、ISSA、QSTA、MGEFO 的提升水平（%）

3.2 仿真结果

从表2 可以看出，QCHIO 相对于CHIO 在所有算例上无论是最优值还是平均值都得到了较大程度的提升，相较于ICHIO1、ICHIO2、ICHIO3、ICHIO4 也得到了不同程度的提升，从而证明了改进策略的有效性。其中相较于ICHIO1，QCHIO 在最优值上的提升大于平均值的提升，由此可以推断加入量子计算算子有助于提升算法的全局开发能力。相较于CHIO2，QCHIO 在大规模问题的LA21、LA26、LA31、LA36 上均得到了较大的提升，由此推断威布尔分布算子在求解大规模问题上具备一定优势。文献[14]指出全局最优解是在所有邻域结构中的局部最优解中找到的，并且某种邻域结构的局部最优解通常接近于另一种邻域结构的局部最优解。相对于ICHIO3、ICHIO4，QCHIO 分别在当前最优解和全局最优解附近进行了邻域搜索，基于实验结果也同样可得出，算法在最优解附近确实可以搜索到有用的信息，从而提升算法的局部搜索能力。

在表3 中，CHIO(50,500) 意为种群大小为50，总迭代次数为500，例如ISSA(100,500)表示在原文中种群大小为100，总迭代次数为500。在表4 中，∆best表示QCHIO 相较于其他算法最优值的提升率，∆avg表示相较于其他算法平均值的提升率，“－”表示无提升，以QCHIO 相对于CHIO 的提升水平为 例，∆best=(CHIObest-QCHIObest)/ CHIObest,∆avg=(CHIOavg-QCHIOavg)/ CHIOavg。

由表3 和表4 可知，QCHIO 相较于CHIO，最优值和平均值均得到了较大提升，尤其是在大规模问题上均取得了10% 左右的提升。相较于ISSA，虽然其设置了更大的种群规模，但QCHIO 在平均值上有7 个算例上均具有不同程度的提升，说明了QCHIO 在一定程度较ISSA 更稳定。相较于QSTA，QCHIO 与其实验参数设置均保持了一致，从平均值角度看，QCHIO 在9 个算例上得到了提升，在最优值上有4 个算例得到提升，3 个算例保持一致，由此得出引入了量子计算和威布尔分布算子的QCHIO 在解决调度问题上相较于QSTA 具有更强的全局寻优能力和稳定性。与MGEFO 相比，该算法总迭代次数为QCHIO 的2 倍，但在10 个算例的最优值上QCHIO 有5 个算例得到提升，3 个算例保持一致，平均值上有9 个算例得到提升，由此可以推断出QCHIO 较于MGEFO 在求解JSP 问题上更具优越性。

3.3 统计学分析

为了进一步验证本文算法与其他算法在仿真结果在统计学上是否存在显著性差异，通过使用95%置信度的配对t检验对各算法在10 个算例上的平均值进行试验并记录其实验结果，见表5。在四组配对数据中显著性水平p均小于0.05，另外，Cohen's d 值是用来衡量效应量大小的，即算法之间差异的幅度大小。当Cohen's d 值越大时，说明算法之间的差异越大。根据常用的分级标准，效应量可分为小、中、大三个等级，对应的临界点分别是0.2、0.5 和0.8。根据表中的数据可知，4 组数据的Cohen's d 值均大于0.8，表示算法之间存在较大的差异性。因此可以得出结论，QCHIO 与所有对比算法在统计学上均存在显著性差异。

表5 各算法配对t 检验结果

4 实例验证

为了进一步验证QCHIO 求解车间调度问题JSP 的可行性和有效性，本文在某公司汽车发动机生产的作业排产问题上进行了例证，根据文献[15]整理了某型号的发动机的生产工件工艺和数据，各工件的加工顺序见表6，加工时长见表7。

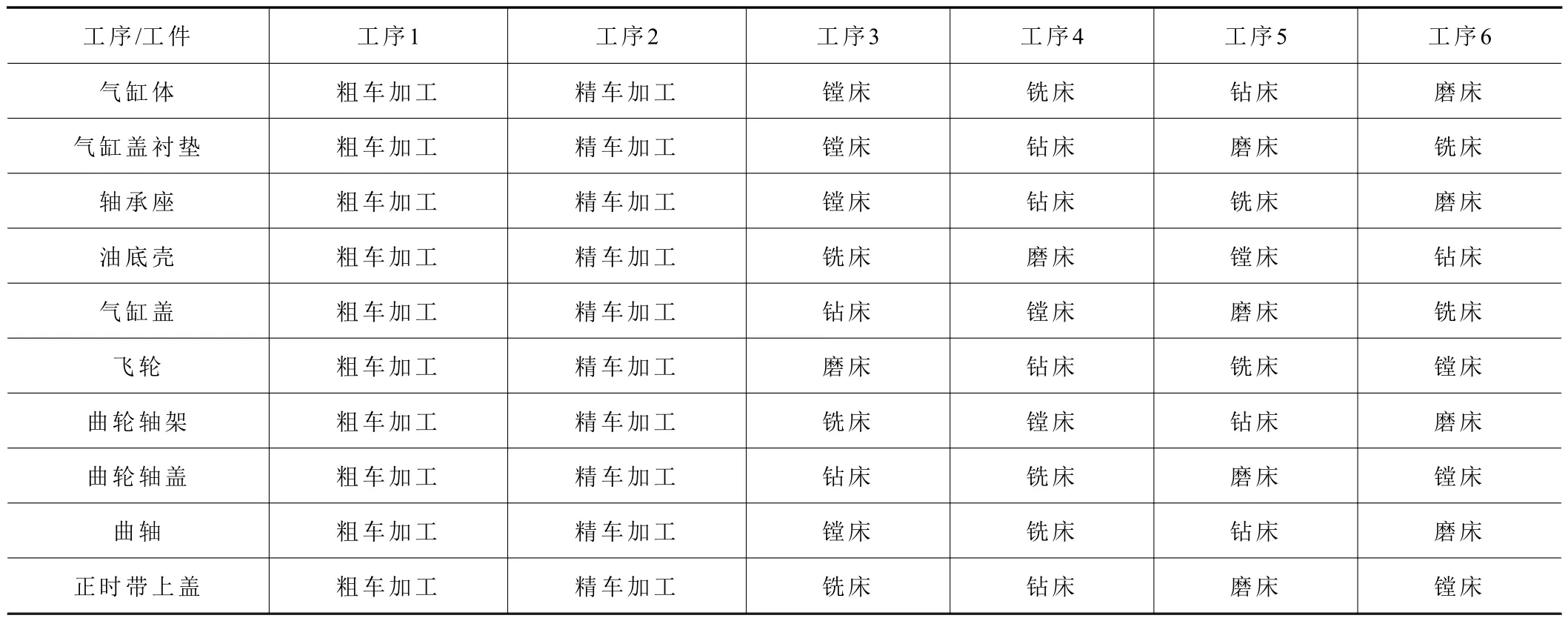
表6 各工件加工工艺

表7 各工件加工时长 min

根据表6 可以看出需要排产的发动机的工件生产过程需要10 个工件，每个工件需要6 道工序，为10×6 规模的问题，解集规模为(10!)6。目前该公司所采用的人工经验调度方式的原则为：优先加工总时长最短的工件，同时在整个调度中尽可能将总加工时长相对较短的工件先加工，同时尽可能保证在调度中排在前面的加工机器能够连续工作，不出现空闲状况，即优先保证粗加工车M1 优先加工，所得到的该型号发动机的主要10 个工件总工时为199 min。

运用本文所提算法QCHIO 对其进行求解，设置种群规模为100，最大迭代次数为100，算法独立运行10 次，所得结果见表8。最优加工方案甘特图如图5 所示。

图5 最优加工方案甘特图

表8 实例求解结果

所得最优加工方案为[3,3,9,10,3,5,9,3,5,4,10,9,7,9,5,6,4,9,10,1,5,1,4,9,7,2,3,10,8,4,6,1,1,5,10,4,7,7,3,8,1 0,5,6,2,8,2,1,4,6,1,8,7,2,6,8,7,2,6,8,2]，加工总时长为122 min。较原始人工调度方法提升了38.7%，较原文提出算法DFACO 提升了10.3%。尽管只是对工件加工工时进行初步改善，但这是在该公司所生产的发动机的其中一种型号，对10 个工件进行的一次10×6 规模的调度优化。考虑到整个公司的产品种类和数量较多，每年实际的生产成品量巨大，并且包括单独外售的零部件，所以从整体上看，这种改善效果和产生的效益是较为可观的。

5 结语

随着全球制造业的发展和竞争的加剧，车间调度作为提高生产车间效率的关键，不断对其进行优化变得越来越重要。本文针对最小化最大完工时间为求解JSP 目标，提出QCHIO 算法，并通过在10个算例进行仿真实验和消融实验，与其他几种算法上进行了对比分析，并对结果进行了显著性分析，最后将其应到一个实际生产案例上，得出了以下结论：

通过对10 个算例的消融结果进行分析，验证了所提算法QCHIO 在改进策略的有效性。通过对算例仿真结果的分析得出QCHIO 具有较强的全局搜索能力，收敛精度较高等特点。引入量子计算算子，通过量子相关性实现全局搜索和快速收敛的目标，增强了算法的全局开发能力，威布尔分布算子进一步增加了算法的多样性和搜索能力，在搜索空间的尾部有更好的拟合性能，能够更好地探索整个搜索空间。β-登山算子和多邻域搜索算子是针对局部最优解问题的改进措施。这两种策略的引入有效地避免了算法陷入局部最优解而无法跳出的问题，提高了算法的局部搜索能力。通过对实例结果分析进一步验证了所提算法的可行性和优越性。

本文的研究对象主要为调度问题中JSP 问题，作为实际生产的简化模型，除了本文应用求解的发动机生产，金属冲压件和弹簧[16]等生产都符合JSP的生产特点，由此看出本文的研究具有一定的代表性，所提算法也可为求解调度问题提供一种思路。但随着绿色制造的提出，越来越多的企业重视企业生产能耗，以求由此来降低成本，因此在同时考虑最大完工时间和能耗的多目标问题上有待进一步研究。