基于多分量LFM信号时频分析的水声多普勒和时延估计研究
宁更新 肖若君 谢 靓
①(华南理工大学电子与信息学院 广州 510641)
②(华南理工大学土木与交通学院 广州 510641)
1 引言
人类海洋活动日益增多,大力发展水声通信和探测技术的需求日渐迫切。海洋水声信道的复杂性体现在可用带宽有限、背景噪声干扰严重、多普勒效应和多径效应严重,且具有时变特性。发送端和接收端的径向相对运动是多普勒效应产生的主要原因。多普勒效应易造成接收端声波信号失真[1,2],为保证信息传输的可靠性,必须准确估计多普勒因子。
估计多普勒因子的方法繁多,时域上利用模糊函数法[3]和块多普勒因子估计法[4],计算简单高效,但模糊函数法的估计精度依赖相关器的数量,硬件成本高计算量大,块多普勒因子估计精度受发送数据帧长度限制。迭代匹配方法[5]避免了估计分量与接收信号在时域的直接相减,多分量信号接近重叠时,各分量估计不会受到严重影响。频域上利用频偏[6]估计多普勒因子的研究广泛,文献[7]利用快速傅里叶变换(Fast Fourier Transform, FFT)确定连续信号频率范围,减小模糊函数法的运算量。在分数阶傅里叶变换(Fractional Fourier Transform, FrFT)域,文献[8]将多普勒因子和FrFT域最优旋转角度关联在一起提供了更精细和灵活的尺度分辨率,但此法在低信噪比的估计精度有待提高。
LFM信号自相关后有锐利的波峰,具相位变化不敏感的特点。许多研究主动发射LFM信号,将其作为水声信号帧同步实现的信号头[9,10]。WVD(Wigner-Ville Distribution)分布是研究LFM参数估计的经典方法,面临多分量LFM信号等非平稳信号有叉项估计误差大的问题。文献[11]利用FrFT和短时傅里叶变换(Short Time Fourier Transform,STFT)的优点,提出了在低信噪比下有效检测多分量LFM信号并估计参数的方法,由此避免交叉项的影响。文献[12]引入了能在参数空间直接显示调频斜率和中心频率的LVD(LV’s Distribution)方法,它能在克服交叉项影响的同时适应高斯噪声和脉冲噪声并存的复杂噪声环境。
为了进一步提升估计精度,一些研究者利用非线性调频模态和来分析多分量信号,如Chen等人[13]提出变分非线性模态分解(Variational Nonlinear Chirp Mode Decomposition, VNCMD)算法获得大带宽信号中不同分量的线性调频模态,随后又提出无需知道信号总分量个数的自适应模态分解(Adaptive Chirp Mode Decomposition, ACMD)[14]算法。模态分解算法预估初始瞬时频率的方法一般基于寻找最大能量的准则,文献[15]采用了脊路重组(Ridge Path Regrouping, RPRG)算法来校正连接多分量信号交叉区域的频率脊线,但在提取出第一条频率脊线后,脊线交叉区域的频率信息会丢失。
本文针对上述问题,提出一种由非完全残差和脊线段匹配结合的ACMD算法(Incomplete Residual& Instantaneous Frequency Segment Matching Adaptive Chirp Mode Decomposition, IRSMACMD)。非完全残差保留了多分量信号交叉区域的部分信息解决了时频脊线断裂的不足,脊线段匹配从接收信号两端开始分段匹配,操作简便且减少了脊线段紊乱错配的概率。利用IRSM-ACMD算法得到多分量LFM信号各分量的初始频率和调频斜率,联合这两个估计参数示出多普勒因子和时延估计算法,提高了多普勒因子估计和时延估计的精度。
2 多分量LFM信号时频分析方法
水声信道复杂多变,利用多分量LFM信号模型描述接收信号,仿真实验示出ACMD结合完全残差估计接收端有交叉多分量LFM信号瞬时频率的效果有待改进,由此提出IRSM-ACMD算法。
2.1 信号模型

其中,fm和km分别是LFM分量m的起始频率和调频斜率。
2.2 ACMD算法


得到第1个估计分量x1(t)后,用X(t)完全减去x1(t)得到第1个残差R1(t)作为公式(3)的X(t)继续估计第2个分量,重复M次得到各分量信号及第M个分量之后的完全残差RM(t)。
图1仿真中,信号起始频率分别是40 kHz,50 kHz, 70 kHz,截止频率分别是65 kHz, 55 kHz,80 kHz,加入信噪比为5 dB的高斯白噪声,每个信号采样频率是300 kHz,信号长度6 000点,STFT窗长是256点。在去除估计的第1个分量后获得第1个完全残差,其短时傅里叶变换(STFT)结果如图1(b)所示,时频域中剩余待估计的分量信号断裂,这直接导致获取时频脊线的误差较大,完全残差迭代处理的方式在准确估计各LFM信号调频斜率与起始频率的效果上仍有欠缺。

图1 ACMD算法结合完全残差处理有交叉的3分量LFM信号
2.3 IRSM-ACMD算法
针对估计分量信号交叉区间断裂、多分量时频脊线提取误差增大的问题,本文提出一个非完全残差函数(Incomplete Residual, IR),它在去除已估计分量的时候添加了一个取值范围为(0,1)的系数εIR保留交叉区间的部分能量。定义非完全残差函数IR(t)见式(5):

非完全残差IR(t)的初始值是X(t),利用ACMD算法从非完全残差IR(t)中分解出的当前分量信号为x˜m(t) ,对应的瞬时幅度为A˜m(t),时频脊线为F˜m(t)(即瞬时频率)。用基于最小二乘法则的拟合方法对时频脊线F˜m(t)进行线性拟合得到k˜m和f˜m以及更新的F˜m(t)。若已估计分量保留的部分能量大于其他未被估计分量的能量,会出现时频脊线重复估计的问题。根据公式(6)判断当前估计的时频脊线是否已经存在:
其中,k是正整数表示已经得到的估计分量信号,k ∈[1,m-1] , ∆F为自定义的频率差值,表示判定两个时频脊线是同一时频脊线时所允许的频率差值范围。如果式(6)成立则表示时频脊线F˜m(t)重复估计,舍弃该时频脊线,如果式(6)不成立则保留该时频脊线,并按式(7)更新阈值残差 IRth(t),无论估计的时频脊线是否重复,IR(t)均按照式(8)更新:
式(9)表明从信号X(t)中去除的分量信号总能量,定义整个算法结束阈值为 (1-εIR)·X(t),依式(10)判断算法是否结束,如式(10)成立,算法结束。

其中,t和F分别表示时间和频率变量,A˜m(t)和F˜m(t)是ACMD算法分解非完全残差得到的信号分量m的瞬时幅度和时频脊线估计值,δ(t)是Dirac函数。
对于低信噪比环境下、时频域交叉复杂的多分量LFM信号,结合非完全残差函数进行迭代的ACMD算法仍有局限性。ACMD算法从输入信号中寻找具有最大能量的分量作为预分量,预分量的估计效果会影响各分量调频斜率、起始频率的提取效果。一些学者探究改进了预估方法,对交叉区间进行多次断开、又多次连接的操作[15],步骤繁琐,本文提出脊线段匹配的方法获得预分量,避开了交叉区间复杂的处理。
设信号的离散化时间点为t=t0,t1,t2,···,tNt-1,根据信号长度Nt设置合适的时频脊线片段长度Lt,时频脊线片段总数不超过Nt/Lt。信号采样周期为Ts,第1次估计时间t0到时间Lt·Ts之间具有最大能量的时频脊线,记为IFSEG1;第2次估计时间tNt-1–Lt·Ts到时间tNt-1之间具有最大能量的时频脊线,记为IFSEG2。KSEG1是片段IFSEG1的斜率,KSEG2是片段IFSEG2的斜率,KSEG1,2是片段IFESG1结尾和IFSEG2开始之间连线斜率,如图2(a)所示。
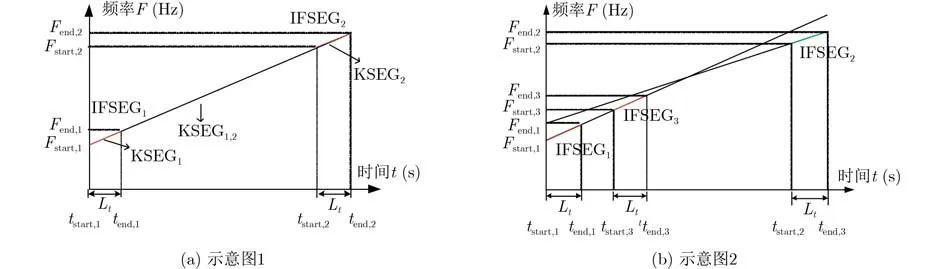
图2 时频脊线片段匹配估计
为了判断两个时频脊线段是否来自同一个分量,定义两个时频脊线片段的方向相关性为

3 多普勒因子以及时延估计
考虑水声信道的多径效应,不同路径具有不同多普勒因子和时延的情况,在多输入多输出系统中,当发送信号是式(1)表示的多分量LFM信号时,它经过一个具有时延和多普勒效应的水下信道后,某一接收端信号为[17]
其中,a′m是接收信号分量m的幅度与信道增益am的乘积,τm是分量m对应的时延,∆D,m是分量m对应的多普勒因子,假设在时间τ开始接收信号,接收信号长度Lr。利用IRSM-ACMD算法对长度为Lr(从时刻τ到时刻τ+Lr)的多分量LFM信号进行处理,得到每个分量的调频斜率kτ,m和时刻τ对应的频率fτ,m,m是信号分量序号, 1≤m ≤M。每个分量的调频斜率kr,m和kτ,m的关系以及频率fr,m和fτ,m的关系为

4 仿真验证
本节对提出的基于多分量LFM信号时频分析的水声多普勒因子和时延估计方法进行仿真验证。首先在高斯白噪声环境下,观察ACMD算法[13]与IRSM-ACMD算法估计瞬时频率值的效果。在单分量LFM信号与多分量LFM信号经过多径信道的情况下,进行两种条件仿真,对比IRSM-ACMD算法、文献[5]、和基于RPRG[15]时频方法得到多普勒因子和时延估计效果。利用多频段的仿真实验验证IRSM-ACMD算法的有效性。
4.1 多分量时频分析方法仿真
依据图1仿真条件,利用ACMD算法和提出的IRSM-ACMD算法按式(11)得到自适应时频谱见图3。图3(a)某一分量的时频脊线出现大幅度抖动,存在明显失真,图3(b)结果贴近仿真的3分量LFM信号。相较于ACMD算法,IRSM-ACMD算法减小了交叉区间断裂缺失带来的估计误差。
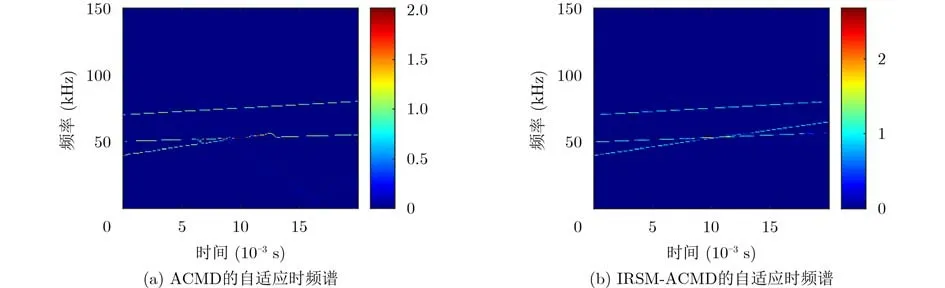
图3 两种算法的自适应时频谱

图4 发送信号为单分量LFM信号的多普勒因子和时延估计均方误差(考虑多径)
4.2 多普勒与时延估计算法对比
仿真1发送单分量LFM信号,时间采样频率200 kHz,起始频率18 kHz,调频斜率2.8 kHz/s,截止频率35 kHz。时频脊线估计的频率增量为8,加入高斯白噪声,信噪比SNR在–2~14 dB。考虑多径效应,假设信道多径数量为3 (LH=3),每条路径对应的多普勒因子和时延仿真参数如表2所示。执行200次蒙特卡罗实验。

表1 IRSM-ACMD时频方法步骤

表2 发送信号为单分量LFM信号时多径信道对应的时延和多普勒因子仿真参数
考虑单分量信号在实际水声信道中的多径效应,在时刻τ接收端得到一个多分量LFM信号,采用IRSM-ACMD算法与文献[5]分别估计了多普勒因子和时延,结果见图(4)。路径1和路径3对应的接收信号在时频域交叉,信噪比在4 dB以下时,路径1和路径3对应的多普勒因子和时延估计均方误差明显要大于路径2的估计结果。SNR在0 dB以上时,基于IRSM-ACMD算法估计的多普勒因子和时延均方误差要小于文献[5]得到的结果。SNR为–2 dB时,路径1和路径3对应的估计结果精度要略差于文献[5]得到的结果,因为路径1和路径3的接收信号在时频域交叉。时频脊线估计受噪声影响较大,可对STFT变换结果降噪来提高IRSM-ACMD方法的抗噪性能。
仿真2的发送信号由3个LFM信号组成,设置∆D,m范围为0.02~0.05,时延τm为0.9~1.5 s,时间采样频率为200 kHz,3分量信号幅度均为1V,时频脊线估计的频率增量为5,加入高斯白噪声,SNR在–2~14 dB,执行200次蒙特卡罗实验。每个分量对应的多普勒因子和时延理论参数如表3所示。
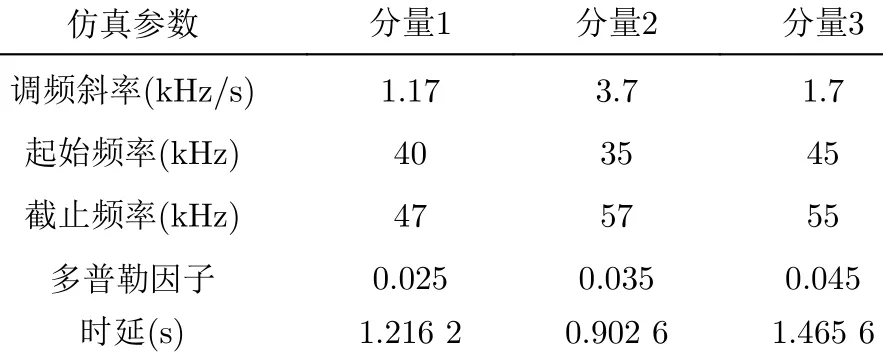
表3 发送信号为时频域有交叉多分量LFM信号时的仿真参数
图5是发送信号为时频域有交叉多分量LFM信号的多普勒因子和时延估计均方误差结果,将本文提出方法与RPRG[15]方法得到的估计结果做对比SNR在6 dB及以下时,IRSM-ACMD各分量的时延估计均方误差都小于RPRG, SNR在2 dB以上时,IRSM-ACMD算法的时延估计均方误差结果基本处于同一数量级,此算法在较低信噪比便获得了时延估计结果的稳定性,SNR在10 dB及以上时,RPRG方法获得了较稳定的时延估计结果。在低信噪比处,IRSM-ACMD算法得到的时延估计均方误差小于RPRG得到的时延估计均方误差,SNR在6 dB以上时,RPRG方法对分量3的时延估计均方误差小于IRSM-ACMD算法的时延估计。
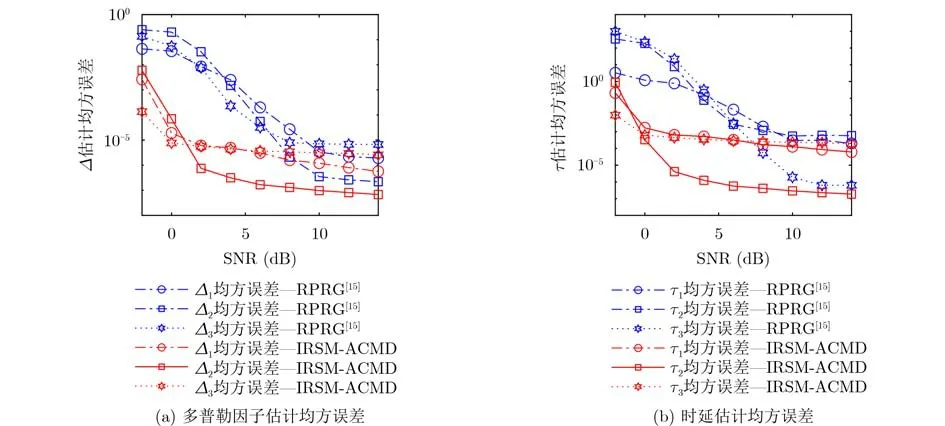
图5 发送信号为时频域有交叉多分量LFM信号的多普勒因子和时延估计均方误差
图6是发送信号为时频域有交叉多分量LFM信号时的多普勒因子和时延估计均值结果。SNR在6 dB以下时,基于RPRG方法得到多普勒因子和时延估计均值在低信噪比时偏离理论值严重, SNR在–2 dB以上时,基于IRSM-ACMD时频方法得到多普勒因子和时延估计均值高度接近理论值。

图6 发送信号为时频域有交叉多分量LFM信号的多普勒因子和时延估计均值
仿真1与仿真2发射的信号处于高频段,仿真3发射低频段的信号,利用BELLHOP模型,设浅海深250 m,声源与目标放置深度分别为120 m,100 m,水平相距800 m,追踪声源为1 500 Hz的声线10条,获得时延范围是0.5~0.6 s。参考BELLHOP模型参数和时延结果,设发送信号的频率范围是0~3 000 Hz,时间采样频率6 000 Hz,3分量信号幅度均设置为1V,时频脊线估计的频率增量为5,加入高斯白噪声,SNR在–2~14 dB,执行100次蒙特卡罗实验。发送较低频段LFM信号以及每个分量对应的多普勒因子和时延理论参数如表4所示。

表4 低频段时频域有交叉多分量LFM信号的仿真参数
图7是低频段时频域有交叉多分量LFM信号的多普勒因子和时延估计均方误差结果,将本文提出方法与RPRG[15]方法得到的估计结果做对比。在0~14 dB的信噪比中,利用IRSM-ACMD的多普勒因子和时延估计值的均方误差均小于利用RPRG方法的多普勒因子和时延估计的均方误差。IRSM-ACMD方法整体估计效果优于RPRG方法,只有在信噪比为–2 dB时,RPRG方法估计分量2多普勒因子的均方误差略微小于IRSM-ACMD算法估计分量2的多普勒因子,误差仍处于相同数量级。IRSM-ACMD算法估计的分量3的均方误差最小,其中多普勒因子估计均方误差可达10–8量级,时延估计均方误差小于10–5量级。

图7 低频段时域有交叉多分量LFM信号的多普勒因子和时延估计均方误差
图8是低频段时频域有交叉多分量LFM信号时的多普勒因子和时延估计均值结果。由图8(a),利用IRSM-ACMD算法的多普勒因子估计均值相较于RPRG方法更接近理论均值,信噪比在–2~10 dB时,利用RPRG方法的多普勒因子估计均值随信噪比的增大逐渐接近理论值,并伴有一些抖动现象,信噪比大于10 dB时趋于平稳并接近理论值,利用IRSM-ACMD算法的多普勒因子估计均值随信噪比增大并逐渐趋于均值,信噪比大于4 dB时接近理论值。由图8(b),利用IRSM-ACMD算法的时延估计均值相较于RPRG方法更接近于理论值,信噪比在–2~8 dB时,利用RPRG方法的时延估计均值随信噪比增大先减小随后出现抖动,信噪比大于8 dB时趋于平稳并接近理论值,信噪比在–2 dB时,利用IRSM-ACMD算法的时延估计均值稍偏于理论值,随着信噪比增大,IRSM-ACMD的时延估计均值都贴近理论值。
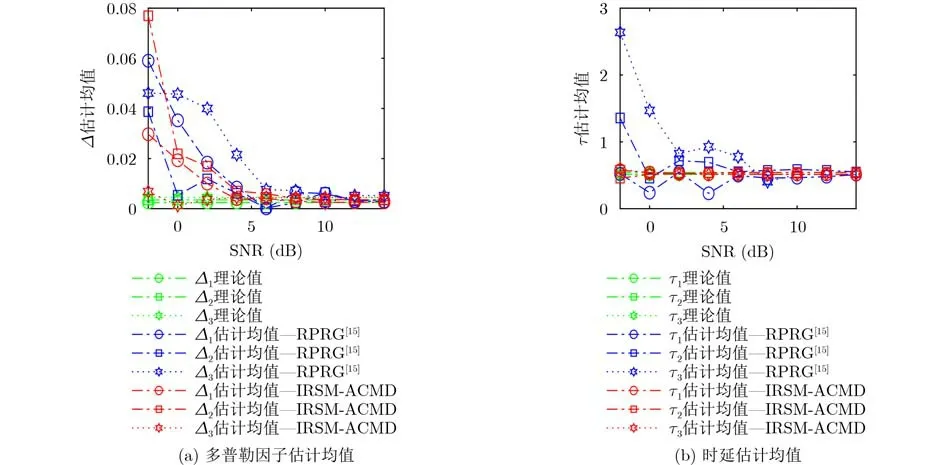
图8 低频段时频域有交叉多分量LFM信号的多普勒因子和时延估计均值
5 结论
针对ACMD算法分析多分量LFM信号过程中交叉区间断裂、时频信息丢失的问题,本文提出了IRSM-ACMD算法,并且将此方法应用到多普勒因子和时延估计中。仿真结果表示,信噪比大于0 dB时,利用IRSM-ACMD算法的多普勒因子估计结果优于对比方法,随着信噪比增大对单一分量的估计均方误差可达10–8。提出方法可满足水声多径传播下的多普勒因子和时延估计,具有较高的估计精度。

