基于伪监督注意力短期记忆与多尺度去伪影网络的图像分块压缩感知

李俊辉 侯兴松

(西安交通大学信息与通信工程学院 西安 710049)

1 引言

分块压缩感知(Block Compressed Sensing,BCS)作为一种信号采集和恢复技术，可以从少量的线性测量中重建原始信号，在核磁共振成像[1]，图像压缩[2]和快照压缩成像[3]等中得到了广泛的应用。

在BCS理论中，给定一幅宽和高分别为W和H的图像X∈RW×H，将其无重叠地划分为Nb个B×B大小的图像块，并对其向量化，得到X={x1,x2,...,xNb}，则可以通过线性测量获得Y

其中，ΦB ∈Rm×n是测量矩阵，n=B×B，设采样率为γ，则m=γ×n；yi ∈Rm为第i个图像块xi ∈Rn的测量值。记式(1)中ΦB所在的矩阵为Φ，其转置矩阵为ΦT。

BCS重建的目标就是从测量值Y中恢复出信号X。由于m ≪n，BCS是一个典型的病态逆问题。为了解决该问题，现有的BCS方法主要分为3类：基于模型的方法；基于端到端的深度神经网络方法；基于端到端的深度展开方法。

传统的基于模型的方法通过优化式(2)来恢复信号X

其中，Xˆ 为恢复的信号；ϕ(X)表示先验正则项；λ是一个超参数，用于约束正则项的强度。

为了解决该优化问题，人们提出了许多非线性迭代优化算法[4–6]，比如正交匹配追踪(Orthogonal Matching Pursuit, OMP)[4]，迭代软阈值算法(Iterative Shrinkage-Thresholding Algorithms,ISTA)[5]和近似消息传递算法(Approximate Message-Passing, AMP)[6]。这些方法通常具有较好的理论解释性，然而，它们的计算复杂度较高，并且在BCS重建中，通常具有严重的块伪影问题。

近年来，受到卷积神经网络(Convolutional Neural Network, CNN)强大的表示能力及其在许多计算机视觉任务中的成功应用的启发，人们提出了许多基于CNN的BCS重建算法[7–9]。这类方法通常通过端到端的学习方式以获取从测量值到相应原始图像的非线性映射网络模型。例如，Mousavi等人[7]设计了一个堆叠去噪自动编码器(Stacked Denoising Autoencoder, SDA)，通过从数据中学习一个结构表示以恢复图像。Kulkarni等人[8]提出了非迭代重建网络(ReconNet)，该网络采用固定的随机高斯矩阵来进行BCS采样，使用全连接网络和6层堆叠的CNN层进行图像重建，并利用块匹配和3维滤波去噪进一步去除块伪影。Gan等人[9]考虑到传统的CNN在提取非局部自相似性上具有较大的局限性，利用Transformer[10]和CNN在提取全局和局部特征上面的优势，提出了一个基于Transformer和CNN联合的BCS方法，即TCS-Net。

相比于传统的基于模型的优化算法，以上基于端到端的BCS方法不需要进行多次迭代重建，这极大地减小了它们的时间复杂度。然而，它们的黑盒子设计使得它们缺乏一定的理论解释性，并且它们的性能严重依赖于超参数的精心选择和良好的架构设计[11]。深度展开网络(Deep Unfolding Networks,DUNs)[12–14]将传统的基于模型的重建迭代算法用深度神经网络进行替代，实现了速度与可解释性之间的平衡。Zhang 等人[12]将ISTA展开成深度学习网络模型，提出了ISTA-Net+算法。在该算法中，每个图像子块被单独的采样和重建，这导致最终生成的图像具有严重的块伪影问题。随后，Zhang等人[13]基于ISTA-Net+提出了优化启发下的可解释深度网络(OPtimization-INspired Explicable deep Network+, OPINE-Net+)，使用独立采样，联合重建的方法。与该方法类似，Zhang 等人[14]将传统方法AMP映射到深度神经网络并提出了AMP-Net，也采用OPINE-Net+类似的方法去除块伪影。然而，OPINE-Net+和AMP-Net只将每次迭代重建的图像作为相邻两个迭代间的输入和输出，而忽略了由于每次迭代去块伪影时，通常会同时去除一些信号和保留部分块伪影这一事实[15,16]，从而影响了它们的重建性能。此外，虽然OPINE-Net+和AMP-Net相比ISTA-Net+在一定程度上缓解了块伪影问题，但是由于它们只使用卷积层和线性整流函数(Rectified Linear Unit, ReLU)堆叠的网络来去除块伪影，缺乏对非局部信息的利用，可能影响最终的重建性能。最近，Shen 等人[17]结合CNN与Transformer可以获取图像的局部和非局部信息的特点，将其嵌入到基于ISTA的梯度下降和软阈值迭代的DUN中，提出了重建性能优异的TransCS算法。实际中，由于图像块内存在非局部相关信息[18]，设计一个具有较大感受野的去块伪影网络更有利于模型从其他相似区域中学习每个图像子块缺失的信息。但具有大感受野的模型通常需要更多的计算资源，而在实际应用中，计算资源可能是有限的。本文通过设计多尺度网络，可以在不牺牲太多性能的情况下更加高效地处理图像。另外，通过使用多尺度网络，可以更好地捕获和融合多尺度信息，从而提高模型对图像局部和非局部信息的感知能力，更有利于重建具有丰富细节和多尺度结构的图像。

本文将基于学习去噪的阈值迭代算法(Learned Denoising-based Iterative Thresholding, LDIT)[6]展开成DUN，提出了基于伪监督注意力短期记忆与多尺度去块伪影网络的图像分块压缩感知(Pseudo Supervised Attention Short-term Memory and Multi-scale Deartifacting based image block compressed Sensing, PSASM-MD)迭代方法。为了从块伪影残差中抽取有用信号，使用伪监督注意力模块(Pseudo Supervised Attention Module, PSAM)中提取部分有用信号，并传递到下一步迭代。此外，在迭代重建中，对每个图像子块使用提出的残差卷积神经网络(Residual Convolutional Neural Network, RCNN)进行单独去噪，然后利用U型网络的多尺度特性和使用Haar小波变换进行上下采样无信息损失的优势，提出基于多尺度的去伪影网络(Multi-Scale Deartifacting Network, MSDNet)，以更好地对拼接后的图像块进行块伪影的去除。本文的主要贡献如下：

(1) 鉴于基于DUNs 的BCS算法在去除块伪影时，通常会去除部分有用信号，本文通过使用PSAM从块伪影残差中抽取有用信号，并将其传递至下一次迭代阶段，实现了短期记忆。这一方法显著提升了重建图像的质量。

(2) 提出了端到端的PSASM-MD方法。在迭代恢复过程中，利用RCNN去除每个图像子块的噪声，然后使用MSD-Net获取去噪后的图像子块间的多尺度特征以更好地去除图像的块伪影。该方法有效地减少了图像块伪影问题的影响，提升了图像的重建质量。

(3) 一系列实验表明，本文方法相比同类的图像BCS方法在客观质量评价指标和人眼视觉上均表现出了更优的重建性能。

本文的结构如下：第2部分，详细介绍了提出的PSASM-MD系统方案，包括整体框架和伪监督注意力短期记忆与多尺度去块伪影网络的设计细节。第3部分展示并分析了实验结果，验证了本文方法的有效性。最后，第4部分对本文工作进行了总结概括。

2 PSASM-MD系统方案

2.1 整体框架

LDIT算法旨在从自然图像集C与仿射子空间{X|Y=ΦX}的 交集处找到唯一的原始图像Xˆ，即

该算法通过逐步迭代去噪的方式恢复图像，具体计算由3步组成

其中， k表示迭代步数；Dk(·)为一个去噪器。可以将中间变量Rk建模为Rk=X+V k，V k表示一个噪声项。结合式(4)和式(5)可得

其中，I为单位矩阵。因此，在第k步迭代重建中，可以使用去噪器Dk(·) 去除噪声项V k，使得重建图像Xk更接近于原始图像X。在LDIT中，作者采用固定的高斯测量矩阵，训练了10个基于去噪卷积神经网络(Denoising Convolutional Neural Network, DnCNN)[19]的去噪器，以即插即用的方式代替Dk(·)。然而，该方法需要存储大量模型参数，且在BCS重建中，存在着严重的块伪影问题。

本文将LDIT应用到图像BCS重建中，将测量矩阵和去噪器Dk(·)使用深度学习网络代替，将该迭代过程展开成端到端的DUN，提出了PSASM-MD，其模型框架如图1所示。PSASM-MD由采样网络和重建网络组成。

图1 PSASM-MD模型框架

在采样网络中，输入图像X ∈RW×H首先被非重叠地裁剪成B×B尺 寸的Nb个 图像小块xi,i=1,2,...,Nb。可以通过yi=ΦBxi测量获得第i个图像块xi的测量值yi。对于一整幅图像，测量值可由式(1)表示。在重建网络中，Y={y1,y2,...,yNb}为输入值，通过K次迭代可获得重建图像XˆK={xˆK1,xK2,...,xˆKNb}。为了尽量避免相邻阶段间只将中间重建图像作为下一步迭代，而存在信号损失的问题，使用PSAM提取块伪影残差中的信号，并送入下一个迭代阶段。通过端到端训练的方式，测量矩阵ΦB和重建网络参数在大数据的驱动下得到更新。需要注意，与文献[14]相同，此处ΦB为可学习的参数。

2.2 伪监督注意力短期记忆与多尺度去块伪影网络

在PSASM-MD网络的迭代重建中，本文提出RCNN对图像小块进行去噪，使用基于多尺度特征的去块伪影网络MSD-Net通过下采样方式扩大感受野，以利用非局部多尺度特征来去除块伪影问题，增强重建图像的整体视觉效果。图2为PSASM-MD的重建网络中第k次迭代的网络结构，其中PSAM被用于传递相邻迭代阶段的短期记忆信息，以尽量避免去除有用信号。

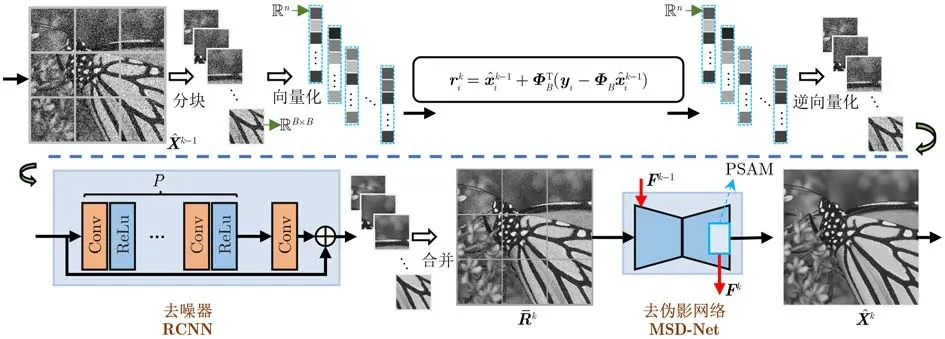
图2 PSASM-MD中第k次迭代网络结构

此处为了去除噪声项vik，本文使用由卷积层和ReLU组成的残差网络RCNN进行噪声去除。具体来说，将rik逆向量化为图像块后，将其并行地送入RCNN进行噪声去除，以缩小块间噪声的差异性。受到DnCNN的启发，本文设计的RCNN结构如图2所示，其中“Conv”为内核大小为 3×3，步长为1的卷积层；ReLU为非线性激活函数，P为“Conv”和ReLU 串联的数量。在第k次迭代后，去除噪声后的Nb个图像子块可由式(10)计算

此外，考虑到去块伪影网络本质上可以看作一个低通滤波器，即去块伪影操作在去除块伪影的同时也去除了信号的某些成分[16]。去块伪影的过程可以表示为

其中，Ek为去除的块伪影。直观地可以看到Ek对最终的去块伪影效果有重要影响。然而由于去块伪影网络有限的信息提取能力，Ek中除块伪影噪声外，通常会包含一些高频图像纹理细节。为了尽量避免在去块伪影时去除部分有用信号，如图3所示，本文通过PSAM中重建的第k阶段的信号Xˆk作为提取第k次迭代中被去除的信号Fk的伪监督信号，产生的Fk被送入到第k+1次的迭代中以实现有用信号的传递。其中，PSAM的网络结构如图4所示，Fikn为重建图像Xˆk的块伪影残差的高维特征，Fk为从残差中提取的信号。图4中的“Conv”表示卷积核为 1×1，步长值为1的卷积层。

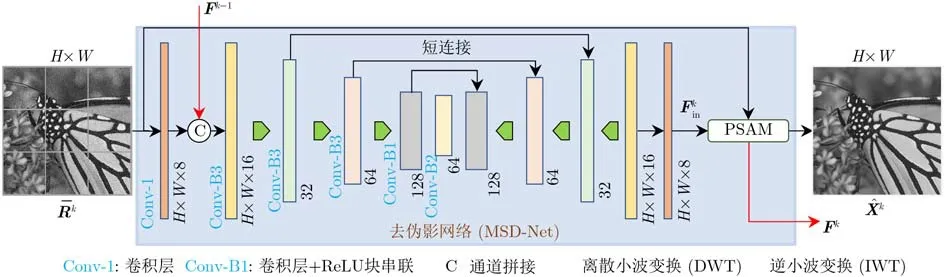
图3 MSD-Net的网络结构

图4 PSAM的网络结构

至此，第k次迭代重建的图像Xˆk与用于传输到第k+ 1 次的多维信号特征Fk可由式(12)获得

其中，式(13)右边第1项为保真项，第2项为用于约束式(9)的正则项；Np表示每次迭代训练中输入图像的总数目；Xj和XˆjK分别表示Np个 图像中的第j个输入图像和对应重建的图像；α为用于调节正则项强度的超参数，其数值被经验性地设置为0.01。

3 实验结果及效果分析

3.1 实验细节

本文使用BSD400[23]中400张图像的亮度分量作为MSD-Net的训练数据集。对每张图片按照步长为47重叠采样成 96×96大小的图像小块。在BCS测量中，设置测量块大小边长B的值为32，即Nb=1 024。本文在BCS中普遍使用的BSD68[23]和Set11[8]两个数据集进行实验仿真，使用两个客观指标[24]：(Peak Signal-to-Noise Ratio, PSNR)和(Structural SIMilarity index, SSIM)来客观度量BCS重建算法的性能。

此外，本文使用高斯测量矩阵来初始化测量矩阵ΦB，并使用Xavier方法来初始化PSASM-MD网络模型的其他网络权重。设置总迭代步数K为8，RCNN中的P为5。为了优化损失函数式(13)，使用带有正则项的Adamw 优化算法[25]进行网络权重优化。在模型训练中，每批次送入模型的图像个数Np=64，设置总训练轮数为50。设置初始学习率为1e–3，当训练轮数每增加5轮，学习率衰减为原先的0.5倍。

3.2 重建性能比较

为了评价本文方法在图像BCS上的客观性能和主观视觉效果，此处综合性地对PSASM-MD进行性能评估。本文使用几个经典的BCS算法：ISTANet+[12], OPINE-Net+[13],AMP-Net[14], TransCS[17]和TCS-Net[9]来进行重建性能的比较。表1和表2分别报道了这些BCS算法在Set11和BSD68上不同采样率下测试结果的平均值。其中，最好的结果用粗体表示。需要注意，表中其他算法的实验结果是使用作者主页提供的代码在其默认参数设置下进行测试所得。从中可以看出，本文提出的PSASMMD方法在Set11上的PSNR和SSIM指标整体上均优于其他BCS算法。在BSD68数据集上，PSNR也优于其他重建算法，而SSIM指标取得了相当的结果。

表1 几种BCS算法在Set11上不同采样率下PSNR(dB)/SSIM的平均值

表2 几种BCS算法在BSD68 上不同采样率下PSNR(dB)/SSIM的平均值

另外，为了从视觉上比较PSASM-MD与其他BCS算法在重建效果上的差异。图5给出了不同BCS算法在Set11中图像上低采样率(γ=4%)和高采样率(γ=10%)下的测试结果。当γ=4%时，可以看出方法ISTA-Net, TransCS和TCS-Net 具有明显的块伪影，这极大地限制了它们的视觉质量。这是由于这几种方法对图像块进行独立采样与重建，从而不利于整幅图像重建时块效应的去除。而方法OPINENet+和AMP-Net进行分块采样和联合重建，显著性地解决了重建图像的块伪影问题，但是由于它们只是简单的使用卷积层堆叠，缺少多尺度信息，以及对相邻迭代间信息的进一步利用，使得其重建图像较为模糊，部分纹理信息丢失较为严重。同理，当γ=10%时，除过ISTA-Net+的重建图像存在较明显的图像伪影外，其他算法的结果相比本文方法PSASM-MD均较为模糊。此外，图6给出了不同BCS算法在BSD68中图像上的测试结果。可以看出，相较于其他算法，本文提出的PSASM-MD方法在重建图像时，没有出现明显的块伪影问题，同时也能更好地恢复图像的结构信息，使得纹理细节更加清晰可见。

图5 不同BCS算法在Set11中“Flinstones”和“Peppers”上的重建结果

图6 不同BCS算法在BSD68中的“test034” 和“test045”上的重建结果

综上，以上实验结果表明，本文提出的PSASMMD方法在客观质量评价和主观质量感知上均达到了先进的水平。

3.3 网络模块消融

为了验证本文提出的PSASM-MD不同网络模块和短记忆功能的有效性，表3给出了PSASM-MD在Set11 数据集上γ=4%和γ=10%采样率下，不同的网络结构的消融实验结果。其中DCNN是AMP-Net[14]中基于CNN堆叠的去伪影网络。以γ=4%为例，从中可以看出，相比于只使用RCNN， DCNN去伪影网络的引入，带来了0.57 dB的增益。而当使用MSD-Net时，获得0.80 dB的增益。此外，通过PSAM引入短期记忆后，模型的PSNR提高了0.91 dB。

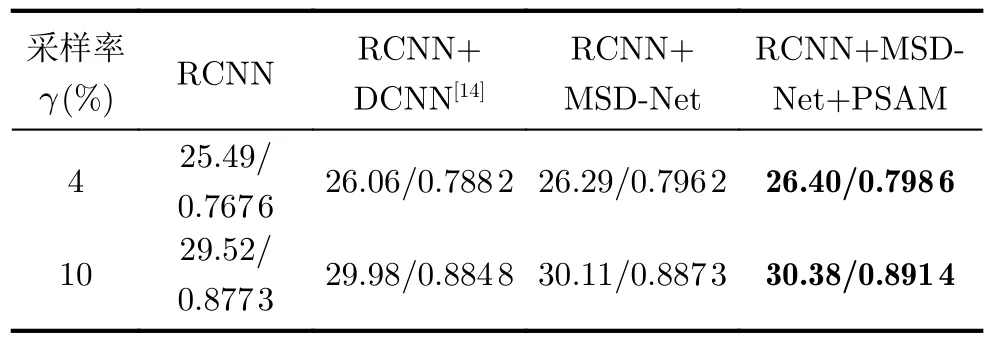
表3 PSASM-MD不同网络结构下Set11上的平均PSNR(dB)/SSIM结果

图7为不同网络结构下中间迭代重建图的特征图以及最终重建图。对比迭代-6阶段中RCNN+MSDNet和RCNN+MSD-Net+PSAM的特征图，可以看出，迭代-6在通过PSAM从迭代-5中引入有用信息的同时，也引入了噪声，但是通过对比最终重建图，可以看出，PSAM的引入促进了网络学习更多的纹理高频信息，有利于恢复更高质量的图像。由此，也可推断，设计更为精细化的伪监督网络模块，更有利于从残差中抽取有用信号，从而可以进一步提高模型的重建效果。

图7 不同网络结构下中间迭代重建图的特征图以及最终的重建图

此外，为了进一步分析PSAM是否可以提取有用信号，以补偿迭代去噪去块伪影中的纹理高频信息的丢失，图8给出了不同迭代步骤下中间重建图像的残差图和对应PSAM提取的特征图以及重建图。可以看出，每次迭代去噪去伪影后，均会去除部分高频纹理信息。如果无PSAM对有用信息进一步的提取，则丢失的信息无法被后续迭代网络利用，从而无法重建出更多的纹理细节。

图8 不同迭代阶段的重建图像的残差图和PSAM提取的特征图以及最终重建图的残差图

综上，可以得出，PSAM与MSD-Net的应用对提高PSASM-MD重建图的质量具有明显的正向作用。

4 结束语

本文提出一种基于伪监督注意力短期记忆与多尺度去块伪影网络的深度展开图像BCS方法。考虑到基于UDNs的BCS算法在去除块伪影时，通常会去除部分信号，本文通过PSAM从块伪影残差中提取有用信号，并将其送入下一步迭代，以增强迭代阶段间的信息传递能力。此外，使用嵌入PSAM的MSD-Net来获取块间的多尺度特征，以更好地去除块伪影。一系列综合的实验结果表明，与当前最具代表性的BCS方法相比，本文方法在人眼视觉和客观评价指标上均取得了更优的重建结果，同时本文算法时间复杂度也较低。