高效前缀约简的三维Hilbert空间填充曲线编解码算法
贾连印 范 瑶 丁家满* 李晓武 游进国
①(昆明理工大学信息与自动化学院 昆明 650500)
②(云南省计算机应用重点实验室 昆明 650500)
1 引言
Hilbert空间填充曲线(Hilbert Space Filling Curve, HSFC)是空间填充曲线家族一个典型代表,其可将高维空间点和1维空间点进行映射和逆映射,同时保持其在原始空间的局部性,相对于Z曲线等其他空间填充曲线,其具有跳变小和空间局部性好等优点。
HSFC广泛应用于空间查询处理[1,2]、图像处理[3]、点云压缩[4]等领域,编解码算法是Hilbert曲线应用的基础。与目前的研究工作多着重于2D HSFC的编解码算法不同[5-8],本文着重于3D HSFC编解码。相对而言,3D HSFC编解码远较2D HSFC复杂[9],该问题的研究对3D图像处理[10]、3D空间索引[11]、人工智能[12,13]等领域有着重要的意义。
早期3D HSFC编解码算法多为基于递归算法,其时间复杂度多为O(k2)(k为HSFC的阶数)。目前的算法以效率更高的迭代算法为主,根据其采用的核心技术的不同,其又可分为基于位操作的算法[14]、基于演化规则的算法[15]、基于状态视图的算法[16,17]等。考虑到基于状态视图的算法简单、直观、高效、易于实现,因此其近年来受到广泛的关注。Zhang等人[16]基于状态视图提出一种适用于不规则边界的3D HSFC编解码算法,Jia等人[17]基于状态视图,提出一种适用于数据向原点偏斜分布的3D HSFC编解码算法。 然而,现有算法通常独立地对每个点进行编解码,而忽略了点之间的关系,从而导致效率低下。本文发现相邻点通常具有一定的公共前缀,充分利用这些公共前缀可提高3D HSFC编码效率。基于此,设计高效的3D状态视图,并提出一种新的前缀约简的3D HSFC编码算法(PR-3HE)和对应的解码算法(PR-3HD),这两个算法通过公共前缀识别、公共前缀约简等技术提高了3D HSFC的编解码效率。在编码阶数为k的窗体时,相对传统算法需对每个数据点编解码k阶,PR-3HE对每个点平均仅需编码2阶,PR-3HD对每个点平均仅需解码8/7阶,复杂度降低到O(1)。实验结果表明,本文算法显著优于现有算法。
2 基础定义和必要的准备
2.1 3D 1阶HSFC的基本状态
Zhang等人[16]和Jia等人[17]采用包含12个基本状态的状态视图,由于基本状态类型的缺失,其在构造3阶及以上的HSFC时,易导致曲线出现跳变,从而降低Hilbert曲线的内聚性。为避免这一问题,本文根据如图1所示的24种3D 1阶基本状态来构建状态视图,基本状态的编号依次为0~23。
2.2 3D HSFC
3D HSFC以递归的方式将空间逐步分割为8个子空间,并通过特定顺序连接这些子空间生成不同的3维Hilbert空间填充曲线。图2展示了状态0的1阶Hilbert曲线中1阶编码与坐标的映射关系,括号外为Hilbert编码,括号内为空间坐标。图3展示了使用分层方式,从24个状态中选取合适的状态,构造出的2阶Hilbert曲线的示意图。
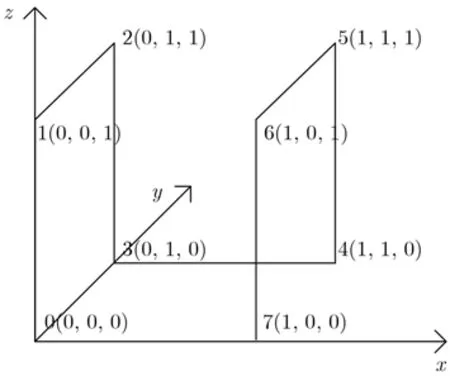
图2 1阶Hilbert曲线
图3 2阶Hilbert曲线
2.3 基础符号与定义
3 编码算法
3.1 3D编码状态视图
在编码阶段,设计了用于存储1阶坐标到Hilbert编码的映射视图CHM和用于存储1阶坐标到下一阶状态的映射视图CSM。给定图1所示的24个基本状态,构建的CHM和CSM分别如表1和表2所示。这两个表的表头中的3位数值分别代表了1阶坐标分量x, y, z的二进制值,而表中的数值则分别表示对应的1阶Hilbert编码(表1)或下一阶状态(表2)。

表1 CHM
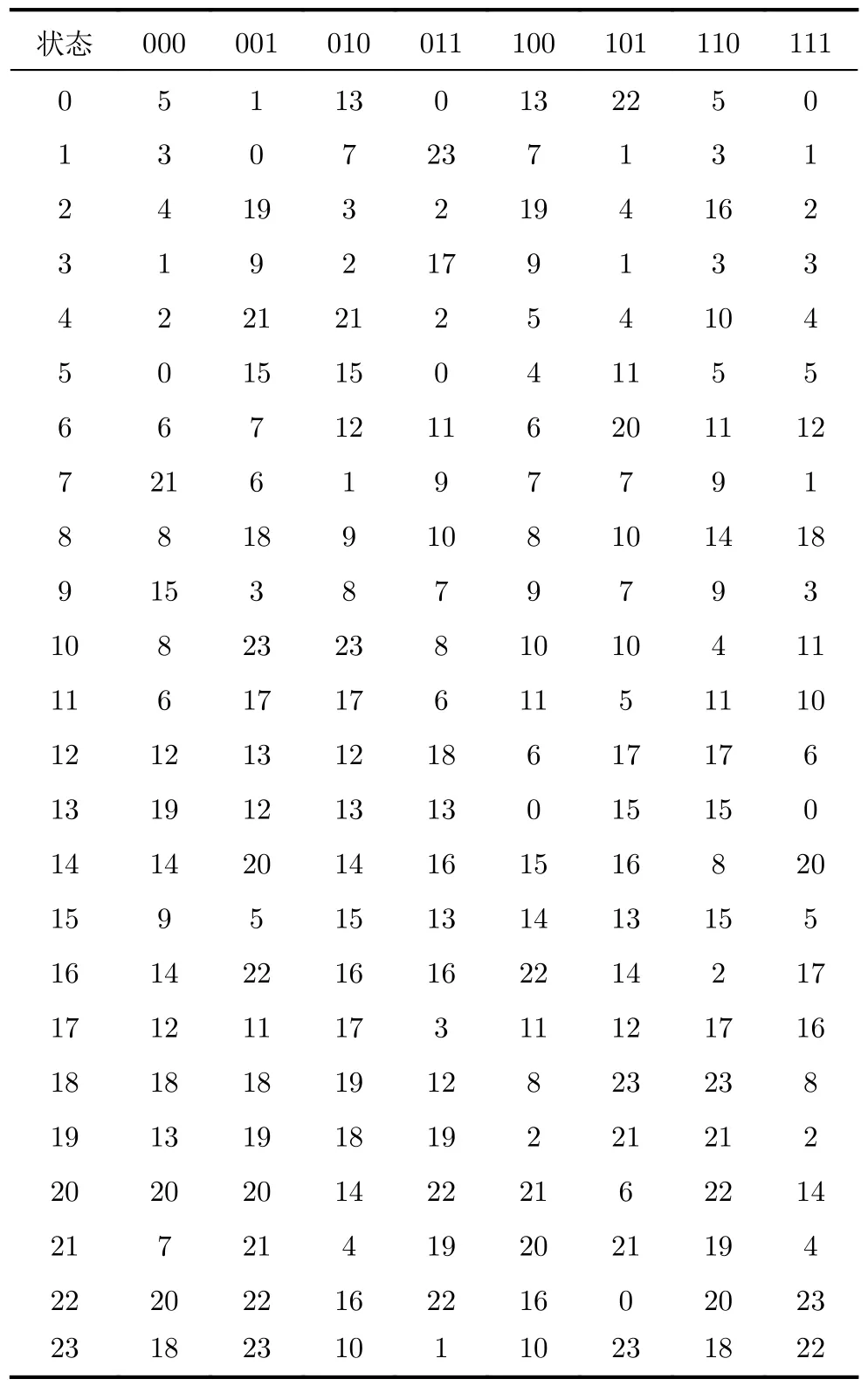
表2 CSM
本文将CHM和CSM设计为两个4维数组。给定第i阶坐标 (xi,yi,zi) 和第i阶的状态,可分别根据Hi=CHM[si][xi][yi][zi],si+1=CSM[si][xi][yi][zi]计算第i阶的Hilbert编码Hi和第i+1 阶状态si+1。本文设定初始默认状态s1=0,即将状态0作为第1阶Hilbert曲线的默认状态。
3.2 编码算法
3.2.1 PR-3HE算法
PR-3HE算法的核心包括公共前缀识别、公共前缀编码约简和约简优化3部分。为便于描述,引入包含p,q和r3个连续编码点的简单模型来对后文算法进行说明,此处p表示已编码点,q表示当前编码点,r表示未编码点。
(1) 公共前缀的识别
PR-3HE需要利用坐标点之间的前缀关系,为此,分别给出坐标分量的最大公共前缀和坐标的最大公共前缀的定义。

(2) 公共前缀编码约简
在识别2个坐标的公共前缀之后,如何利用公共前缀来提高编码效率是本文需要解决的核心问题。PR-3HE算法依托如下的定理。
定理1 点p和q对应的前 |Pp,q|阶编码值相同,第 |Pp,q|+1阶状态相同。

(3) 公共前缀编码约简的优化
记忆数组M解决了p的已编码信息对r编码的支持,然而其同样存在以下3个需要解决的问题:(a) |Pq,r|>|Pp,q|时 ,q和r比p和q有更多的公共前缀,M不能用于从 |Pp,q|+1阶 到 |Pq,r|阶 的编码;(b)r之后的坐标和p的公共前缀可能非常小或没有公共前缀,M中静态存储的p的状态信息无法用于r之后点的编码;(c) 坐标点编码顺序对公共前缀的长度有重要的影响,如何最大化利用M提高编码效率?
对问题(a)和(b),为克服静态存储p的状态的不足,引入M的动态更新机制。在编码q时,动态地将M的从 |Pp,q|+2到 |Pq,r|+1位置的状态更新为q的对应阶的状态,从而使得M可支持r从1到|Pq,r| 阶的编码,即Mr总等于 |Pq,r|。该更新是动态的,在编码r时同样对M进行更新,故M可支持r之后坐标的编码。
图4展示了当k=8 时, |Pq,r|≥|Pp,q|和|Pq,r|<|Pp,q| 2种情形下编码示例。图中假定p,q和r为同一竖线上的3 点且Xp=Xq=Xr=100101102,Yp=Yq=Yr=011010012。坐标栏某个点对应的绿色方框内的部分代表该点与前邻点的公共前缀,记忆数组栏蓝色方框内的部分表示需要更新的阶,Hilbert编码栏红色方框内的部分表示需要迭代编码的阶。图4(a)中,因 |Pq,r|=7≥|Pp,q|=3,故需对记忆数组的第5~8阶进行更新,而图4(b)中,因|Pq,r|=6< |Pp,q|=7,故无需更新操作。

图4 编码示例
考虑到两个坐标越接近,其倾向于有更多的公共前缀,故引入蛇形扫描的机制依次编码坐标点。以图6所示的3D窗体为例,蛇形扫描先从x=0面开始,自下至上依次编码y=0列的所有点,然后自上至下编码y=1 列的所有点,直至y=2k-1列,从而编码完x=0面。然后按类似的规则编码其他面。通过蛇形编码,连续编码的点为距离接近的位置点,有着较多的公共前缀,因此可尽可能地降低M的更新次数,最大限度地提高编码效率。
编码当前点q的基本流程如图5所示,对应的编码算法如算法1所示。

图5 编码当前点 q的流程图
3.2.2 编码效率分析
迭代编码次数是影响编码效率的关键因素,以3阶3D窗体为例,PR-3HE部分需要迭代编码的次数如图6所示。此外,给出PR-3HE编码效率的详细分析如下:

图6 迭代编码的次数(3阶)
定理2在对一个k阶窗体进行编码时,PR-3HE算法对每一个点平均编码阶数小于2。
证明将整个窗体分为5部分:a1(第1个点需要迭代编码的次数,图6中用黄色菱形标记),a2(除去a1,在y=0,z=0这一条直线上的点需要迭代编码的次数,图6中用绿色正方形标记),a3(在 mod(x,2)=1,y=2k-1,z=0这一条直线上的点需要迭代编码的次数,图6中用红色三角形标记),a4(除a1,a2,a3之外进入每一列的第1个点需要迭代编码的次数,图6中用蓝色六边形标记),a5(其余坐标点需要迭代编码的次数,图6中其余未标记部分),各部分编码次数计算如下:

算法1 PR-3HE

4 解码算法
4.1 解码状态视图
解码阶段设计用于存储Hilbert编码值到1阶坐标的映射视图HCM和用于存储Hilbert编码值到下一阶状态的映射视图HSM。给定图1所示的24个基本状态,构建的HCM和HSM如表3和表4所示。
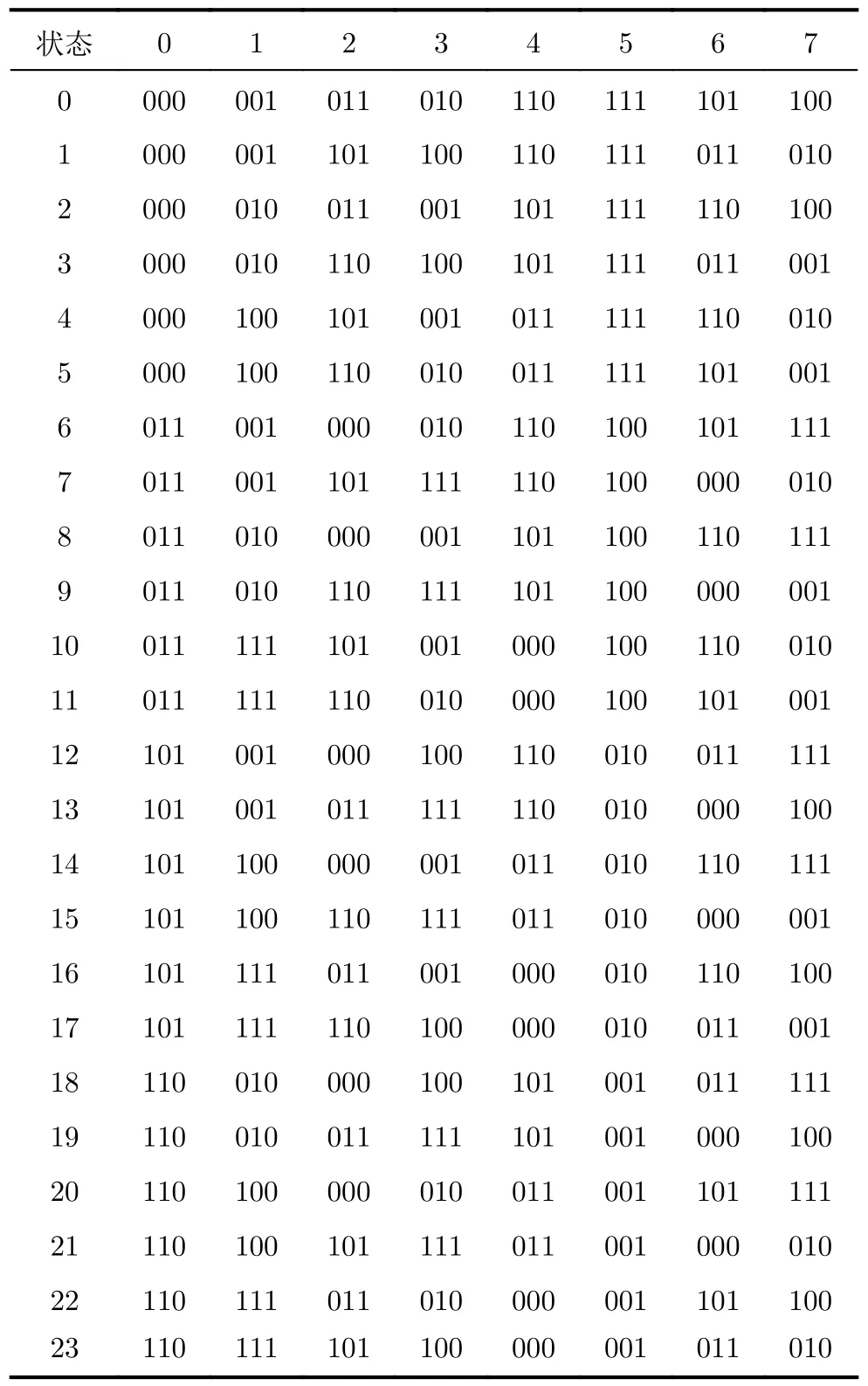
表3 HCM
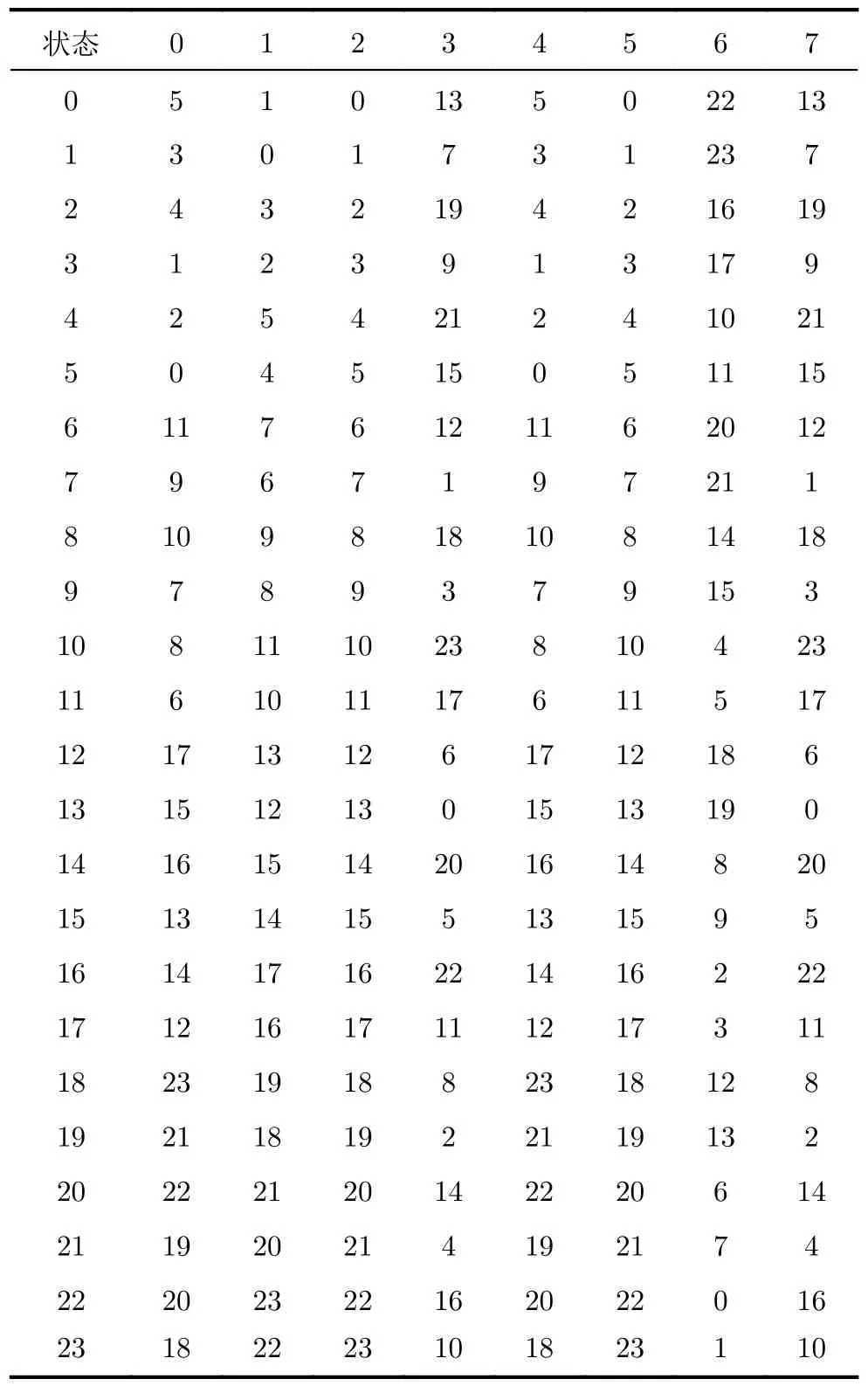
表4 HSM
给定第i阶的Hilbert编码和第i阶状态si,可根据xiyizi=HCM[si][Hi]和si+1=HSM[si][Hi]分 别获得第i阶的坐标值和第i+1 阶状态si+1。
4.2 解码算法
PR-3HD算法

对解码效率分析,按编码类似的思路,可证明对于一个k阶窗体,PR-3HD对每个点的平均解码次数少于 8/7。限于幅面,此处未给出详细的证明过程。
5 实验
5.1 实验环境
实验主要硬件平台:CPU:Intel(R)Core(TM)i7-7700 CPU@3.60 GHz, RAM:16 GB (2 400 MHz),系统环境为Windows 11,编译器为Visual Studio 2019。
5.2 实验数据集
本文采用了以下两个模拟数据集和一个真实数据集。
2016年山东疫苗事件发生后,黄梅立即结束休假,毫无怨言地服从领导安排。2016年3月18日~4月19日,黄梅连续参加两轮对辖区内的疫苗经营企业拉网式全面排查,带领检查组查到了国家总局通报中的上线人员“王忠林”。随后参与对贵州某医药有限公司调查,并对该公司库存的25个品规疫苗、484笔疫苗采购和5275笔医药销售进行逐笔调查。
窗体数据集:分别设置阶数k=6, 7, 8, 9, 10,生成不同窗体大小的数据集。
离散数据集:非重复地随机取点坐标的数据集。生成以下两种类型的离散数据集:(1)固定坐标数量N=1 500万,阶数k=8, 12, 16, 20的离散坐标数据集;(2)固定阶数k=8 , 坐标数量N=100万,200万, 400万, 800万, 1 200万, 1 600万, 2000万的随机坐标数据集。
GeoLife数据集:该数据集为微软亚洲研究院GeoLife项目收集的北京市GPS轨迹数据[18]数据集,包含182个用户在2007年4月至2012年8月间的17 621条轨迹。轨迹的总距离为1 292 951 km,共有24 876 978个坐标点,每个坐标点包含纬度、经度和海拔信息。由于数据集中存在分布于北京市之外的异常点,本文选取位于北京市内的GPS数据作为实验数据,选取坐标范围为x ∈[39.524 420, 40.324 200],y ∈[115.903 388, 116.903 388],z ∈[–100, 100],总计选择了15 871 978个坐标点。
这3个数据集中,窗体数据集代表数据点紧密相邻的情形,即同一水平线或垂直线上的相邻两点距离为1;离散数据集中的数据点随机分布,相邻两点的平均距离往往远大于窗体数据;而Geo-Life数据则介于二者之间,相邻两点的横坐标之间、纵坐标之间可能具有较长的公共前缀。
将本文算法与MOORE[14], LI[15], ZHANG[16],JFK[17]等算法进行比较。为便于描述,为各编码算法增加后缀“-3HE”,为解码算法增加后缀“-3HD”。对所有基于状态视图算法统一采用24个状态视图。
5.3 编码效率对比
离散数据集、窗体数据集、GeoLife数据集上不同编码算法的编码效率对比分别如图7、图8、图9所示。其中窗体数据集的纵坐标为对数坐标。在GeoLife数据集中采用其原始轨迹顺序进行编码。

图7 离散数据集上编码效率对比
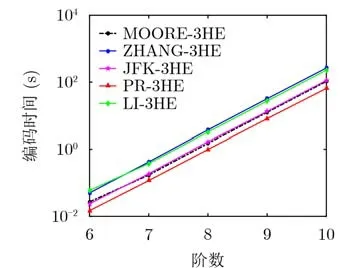
图8 窗体数据集上编码效率对比
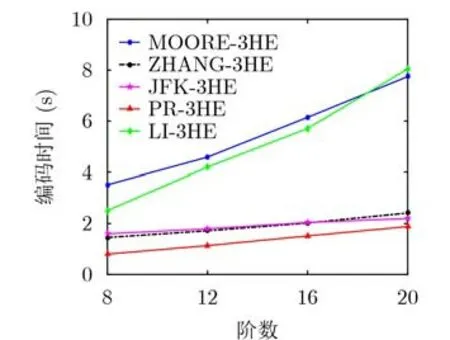
图9 GeoLife数据集上编码效率对比
由图8可见,所有算法的编码时间均随着阶数增加而增加。相较而言,PR-3HE是所有算法中效率最高的,当k=10时,PR-3HE编码仅需65.012 s,而ZHANG-3HE需要104.829 s, PR-3HE比ZHANG-3HE效率提升61.24%,比MOORE-3HE快4.063倍,比LI-3HE快3.512倍。通过进一步分析发现,PR-3HE在6, 7, 8, 9, 10阶下的平均编码阶数分别为1.905, 1.945, 1.969, 1.982和1.990,与定理2分析一致,而ZHANG-3HE的编码阶数则为6, 7, 8, 9, 10。可以预见,随着阶数增加,PR-3HE相对其他算法的优势还将进一步增大。
由图9可见,PR-3HE在GeoLife数据集上的表现优于其余算法,当阶数k分别为8, 12, 16, 20时,PR-3HE算法编码分别需要0.799 s, 1.136 s, 1.513 s,1.880 s,其运行速度比ZHANG-3HE最高快44.99%,比MOORE-3HE快3.403倍,比LI-3HE快3.279倍。在k为8, 12, 16, 20阶时,PR-3HE的平均编码阶数分别为:1.340, 3.901, 7.368, 11.156。相对而言PR-3HE在GeoLife上的优势不如在窗体数据集上明显,其原因是GeoLife为离散数据集,相邻编码点的公共前缀相对较窗体数据集小。此外,随着阶数的增加,坐标之间的距离逐步变大,数据集趋向稀疏,因此算法效率有所降低。
5.4 解码效率对比
离散数据集、窗体数据集、GeoLife数据集上不同解码算法解码效率对比分别如图10、图11、图12所示。

图10 离散数据集上解码效率对比
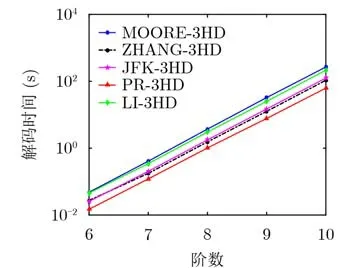
图11 窗体数据集上解码效率对比
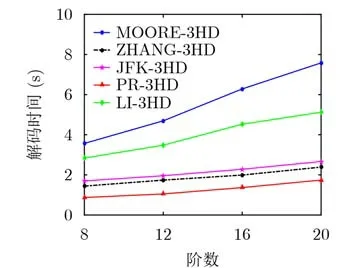
图12 GeoLife数据集上解码效率对比
由图10(a)可见,PR-3HD在离散数据集上的表现优于其余算法,当k为8, 12, 16, 20阶时,PR-3HD的平均公共前缀分别为6.857 1, 7.240 5, 7.243 7,9.007 9。由图10(b)可见,当固定k=8时,PR-3HD算法的效率而随着坐标数量N的增大而不断增加。这是因为当k保持不变时,坐标数量在不断增加,编码值之间有更多共同的阶,从而使得PR-3HD的优势不断扩大。
由图11可见,PR-3HD是所有算法中效率最高的。在k= 10时,PR-3HD解码仅需62.409 s,而ZHANG-3HD需要107.174 s。PR-3HD的运行速度比ZHANG-3HD快71.28%。比传统算法MOORE-3HD快4.27倍,比LI-3HD快3.42倍。可见,PR-3HD受益于前缀约简,具有更高的效率。
由图12可见,PR-3HD优于其他算法,当阶数k分别为8, 12, 16, 20时,PR-3HD仅需要0.872 2 s,1.051 s, 1.367 s, 1.743 s的解码时间。其效率比ZHANG-3HD最高可提升39.62%,比MOORE-3HD可提升3.597 0倍,比LI-3HD提升2.309倍。进一步分析,在阶数k为8, 12, 16, 20阶时,PR-3HD的平均解码阶数分别为:0.061, 1.162, 4.182,7.754。在GeoLife数据集上,PR-3HD相对其他算法仍有明显优势,但优势相对窗体数据集有所减少,其原因在于GeoLife为离散数据集,相邻编码值之间公共前缀相对窗体数据集有所降低。
6 结束语
本文针对现有算法单独编码的缺点,提出了时间复杂度为O(1)的3D编码算法PR-3HE和3D解码算法PR-3HD。通过利用相邻点的公共前缀信息,实现跳过公共前缀的编码和解码,通过引入了公共前缀的定义和识别、公共前缀约简及多种优化技术提高编解码效率。实验结果表明,本文算法相比MOORE算法,效率提高近4倍。下一步拟将本文算法扩展到高阶高维。此外,考虑到现实中数据分布多具有局部聚集特性,因此可将本文算法应用于该类场景。

