基于随机骨料的混凝土边界效应影响研究

胥民尧,王 耀,秦 煜

(1. 盐城工业职业技术学院 建筑工程学院, 盐城 江苏 224005; 2. 重庆交通大学 土木工程学院, 重庆 400074; 3. 中铁二院重庆勘察设计研究院有限责任公司, 重庆 400023)

0 引 言

混凝土结构及其构件长期暴露在露天等复杂环境中,多种有损结构性能的物化反应会直接作用在构件的边壁层,长此以往会影响到构件的耐久性及力学性能。受模板影响,构件边壁层与内部骨料分布有明显差别,即骨料分布存在边界效应[1]。P.C.KREIJGER[2]采用将切片压碎并分离骨料的方法对边界效应进行了测量,发现从边壁层到构件内部的骨料体积分数呈现出先增加,然后再稳定的趋势,但该方法可能会造成骨料破坏,存在一定误差。

随着计算机技术发展,图像识别及数值模拟技术被广泛应用于混凝土内部骨料边界效应及分布特征的研究。杨进波等[3]通过图像处理技术对混凝土边界层效应进行了测定,发现当骨料从边界向内部延伸时,其体积分数逐步增加的规律;M.STROE-VEN[4]基于离散元技术对骨料动态堆积时的边界效应进行了研究,发现堆积密度是由边壁层向内部呈先增加然后逐渐波动至稳定状态的规律;许文祥等[5]通过建立二维椭圆形随机骨料模型,得出骨料分布曲线为上升、下降、上升、最终趋于稳定,边界效应层厚度介于19.75～24.75 mm的结论。针对边界层厚度,不同学者的结论存在着较大差异甚至相反。杨进波等[3]研究发现,在合理的骨料级配条件下,混凝土边界效应层厚度约等于最小粒径,为5 mm;郑建军等[6]将骨料假定为二维圆形形态,通过随机骨料模型发现边界效应层厚度约等于最大粒径,为16.9 mm。由此可知,关于边界层效应的影响规律存在争议,有必要对边界层规律及影响因素展开深入研究。

笔者以再生骨料作为集料体,通过图像识别技术研究了骨料的边界效应。基于数值模拟技术,通过建立圆形、椭圆形、凸多边形等3种形态的随机骨料模型,系统分析了骨料形状、长径比、粒径及表面棱角等特征对边界效应的影响规律。

1 基于图像识别的数值模型

数字图像处理(digital image processing, DIP)是一种计算机处理技术,能将数码相机、扫描仪等获得的电子图片转换为二维像素图像,通过特定软件或代码提取像素并获得图像信息。该技术被广泛应用于混凝土材料宏观[7]及细观尺度[8]的性能研究。在细观尺度层面,数字图像处理技术被广泛应用于细观尺度建模[9]、骨料特征分析[10]、再生骨料附着砂浆含量统计[11]、骨料粒径分布研究[12]、骨料体积分数及边界效应分析[3]、沥青路面均匀度[13]等领域。笔者所建立的数字图像处理技术主要包含分水岭算法修正图像缺陷、分段变换三值化处理和图像滤波降噪等3部分。

1.1 分水岭算法修正图像缺陷

再生混凝土试件内部不可避免地会产生一些杂质或存在微小缺陷,且切割可能会对试件端部造成破坏。传统方法是通过PS软件对图片进行处理,从而消除影响。但对断面内部的干扰点,其过程不但复杂还会产生一定误差。笔者将利用分水岭算法对图像进行预处理,其流程如下:

1)将图像灰度化,并转换为梯度图;

2)根据灰度值相近原则,将梯度图像分割成若干个封闭区域,并设定一个测地距离阈值;

3)搜寻灰度值最小区域,并向外增长,若相邻区域灰度值小于设定阈值,则将该区域淹没。

梯度图像输出如式(1):

grad[f(x,y)]=

(1)

断面按照分水岭算法处理前后对比如图1。由图1可看出:经分水岭算法处理后,附着砂浆及新砂浆内部的白色及黄色干扰点已被消除;同时断面上部边缘因切割造成的破损和切割痕迹也被消除,这表明该算法处理效果较为理想。

图1 分水岭算法修正图像Fig. 1 Modified image processed by watershed algorithm

此时砂浆基体颜色为灰色,继续对断面进行灰度修正处理,将其修正为白色,为精确识别骨料形态奠定基础,修正后的图像如图2。

图2 断面灰度值修正Fig. 2 Grayscale value modification for cross-section

1.2 分段变换三值化处理

修正后的图像为彩色图像,需要将其转换为灰度图像。根据分辨率生成像素点,读取灰度图像内像素点的灰度值,生成灰度矩阵,矩阵值介于0～255。灰度矩阵可用二维离散函数表示:

(2)

式中:(x,y)为像素点定位坐标;m(x,y)为该像素点的灰度值;a、b分别为图像大小。

从宏观层面上看,断面由骨料、水泥及附着砂浆三相介质组成,各相介质具有特定的颜色范围。因此需要对图像进行三值化处理,并标记三相属性所在图像位置,如图3。由图3(b)可知:骨料、附着砂浆及水泥基体的像素点灰度值阈值范围分别为0～30、 30～200及200～255。

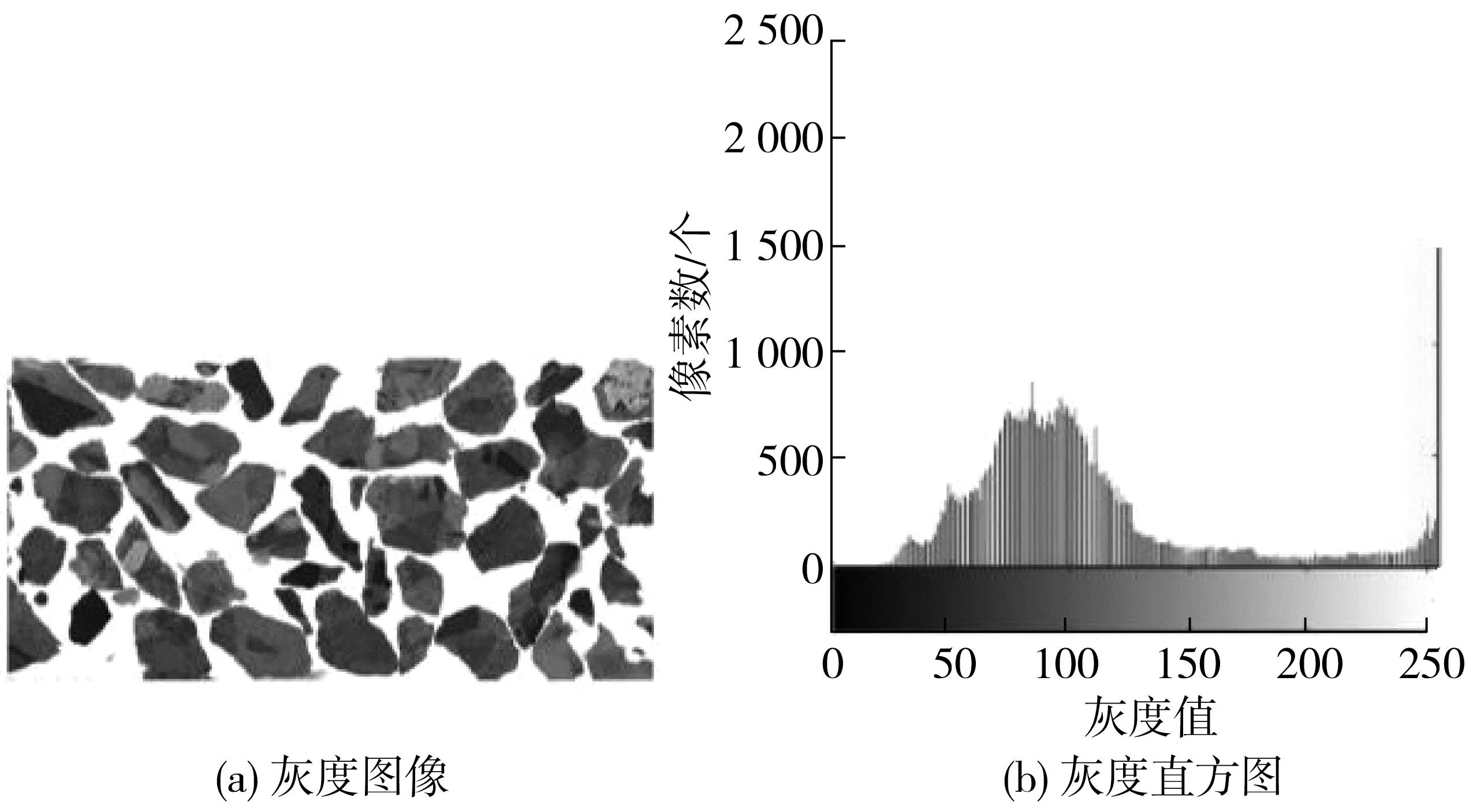
图3 灰度图像Fig. 3 Grayscale image

根据三相介质像素点灰度值范围,通过函数对三相介质进行属性赋值:

(3)

式中:α、β分别为骨料、附着砂浆及水泥基体像素点灰度阈值分界值;g(x,y)为像素点对应的介质属性。

需要注意,三相介质的灰度值阈值范围并非固定,不同断面的阈值需要根据直方图确定。

1.3 图像滤波降噪

图像在拍摄时不可避免的存在噪声影响,需对图像进行滤波除噪,降低噪声干扰。常用的图像滤波方法有中值滤波、均值滤波、自适应滤波等。笔者采用中值滤波进行处理,假设二维图像区域为N,图像宽度为a,高度为b,则中值滤波表达为:

(4)

式中:g(i,j)、f(i,j)分别为中值滤波之后、之前的灰度值;N一般取奇数。

中值滤波示意如图4。图4(a)中:区域为3×3矩阵,9个值的中间(灰色区域)是8;图4(b)中:将这9个值从小到大排序,则中间值为14,则原中间位置的8替换为14。

图4 中值滤波Fig. 4 Median filtering

通过上述步骤,将数码图像转换为由骨料、附着砂浆及砂浆基体三相属性值组成的数据库。数据库中包含各像素点编号、坐标及各像素点属性值,为附着砂浆含量统计及再生混凝土数值模型建立奠定基础。

2 基于随机骨料模型的边界效应

笔者基于图像识别技术,对骨料的边界效应进行了研究,将获得的骨料密度曲线与其他学者研究结果进行对比,验证了该算法的适用性。基于圆形随机骨料模型对边界效应及分布密度曲线进行了分析;基于椭圆形及凸多边形随机骨料模型对骨料形状、粒径、长径比及表面棱角数量等因素对边界效应及密度分布曲线的影响规律进行了研究。

2.1 骨料边界效应算法

骨料密度曲线如图5。图5中:建立与长边平行且距离边界为x的直线,该直线截取的长度与长边比值即为骨料密度分布函数。由于模型两侧的密度分布曲线基本对称,故笔者仅统计到模型的中心位置,即x=L/2,L为试件的短边长度。

图5 骨料密度曲线取值Fig. 5 The value of aggregates density curve

采用文献[11]中的再生混凝土试件对算法的可行性进行验证,如图6。试件共分为4.75～9.50、9.50～12.70、12.70～19.00 mm等3种骨料粒径,每种粒径包含两个试件,试件断面图尺寸取350 × 525像素,将两侧模型边界到中心区域的密度曲线均值作为该模型的骨料密度曲线。

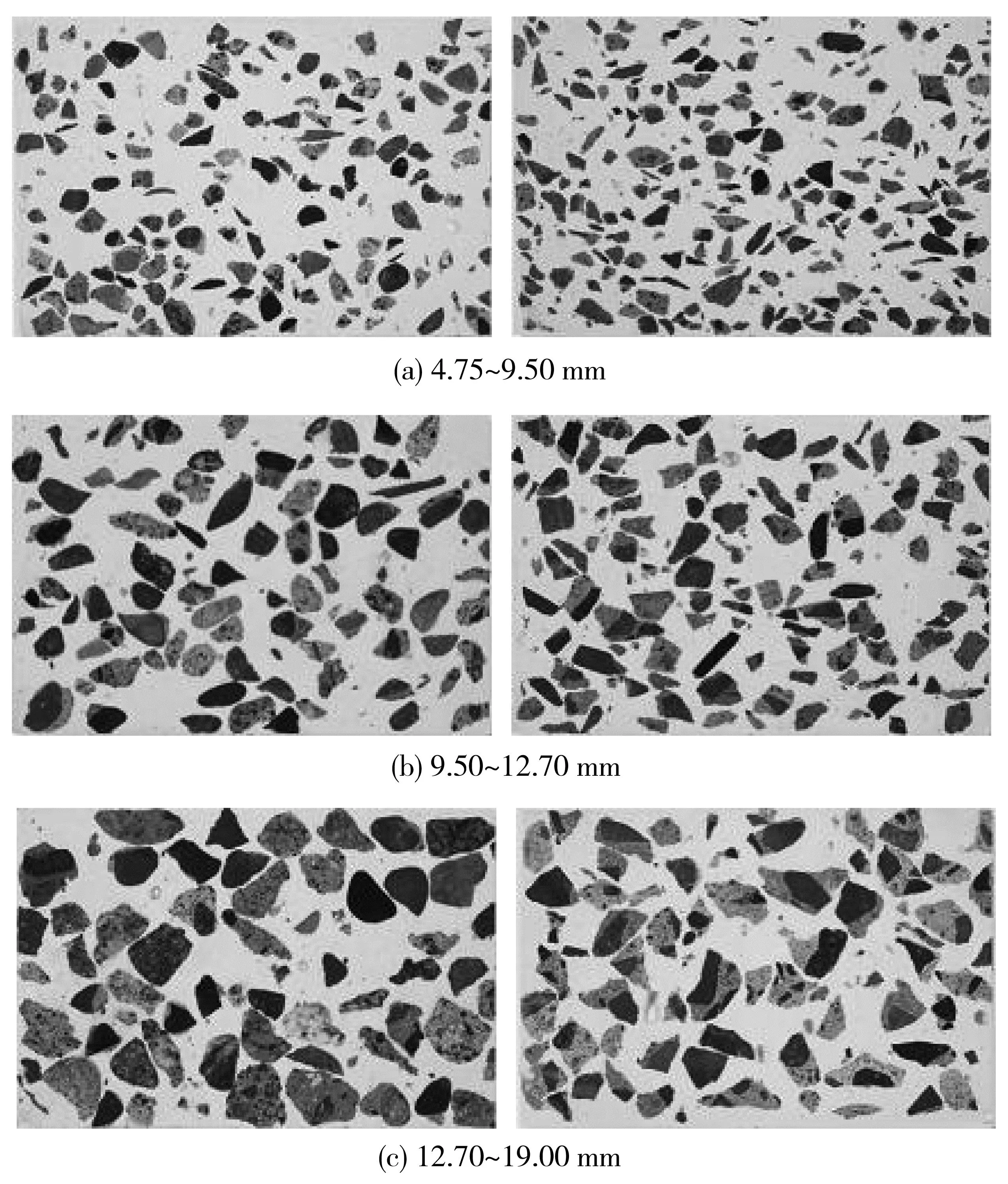
图6 3种再生骨料尺寸的试件断面Fig. 6 Cross-sections of three types of recylced aggregate size

通过图像分析方法获得的粒径4.75～9.50 mm骨料密度分布曲线,如图7。由图7(a)可知:密度分布曲线大致可分为3部分(上升段、下降段及波动段),但由于试件样本数仅有两个,未出现水平段;由图7 (b)可知:密度曲线随边界距离变化的规律基本吻合。

图7 再生骨料密度分布曲线Fig. 7 Density distribution curve of the recycled aggregate

图8为骨料粒径对边界效应的影响规律。整体而言,随着粒径增加,效应层厚度呈现增大趋势,且骨料含量峰值厚度也略有增加,但增加幅度较小;同时波动段骨料含量随着粒径增加逐渐增大,波动段平均值基本等于试件内的含量,这与基于随机骨料模型的研究结果基本吻合[6]。

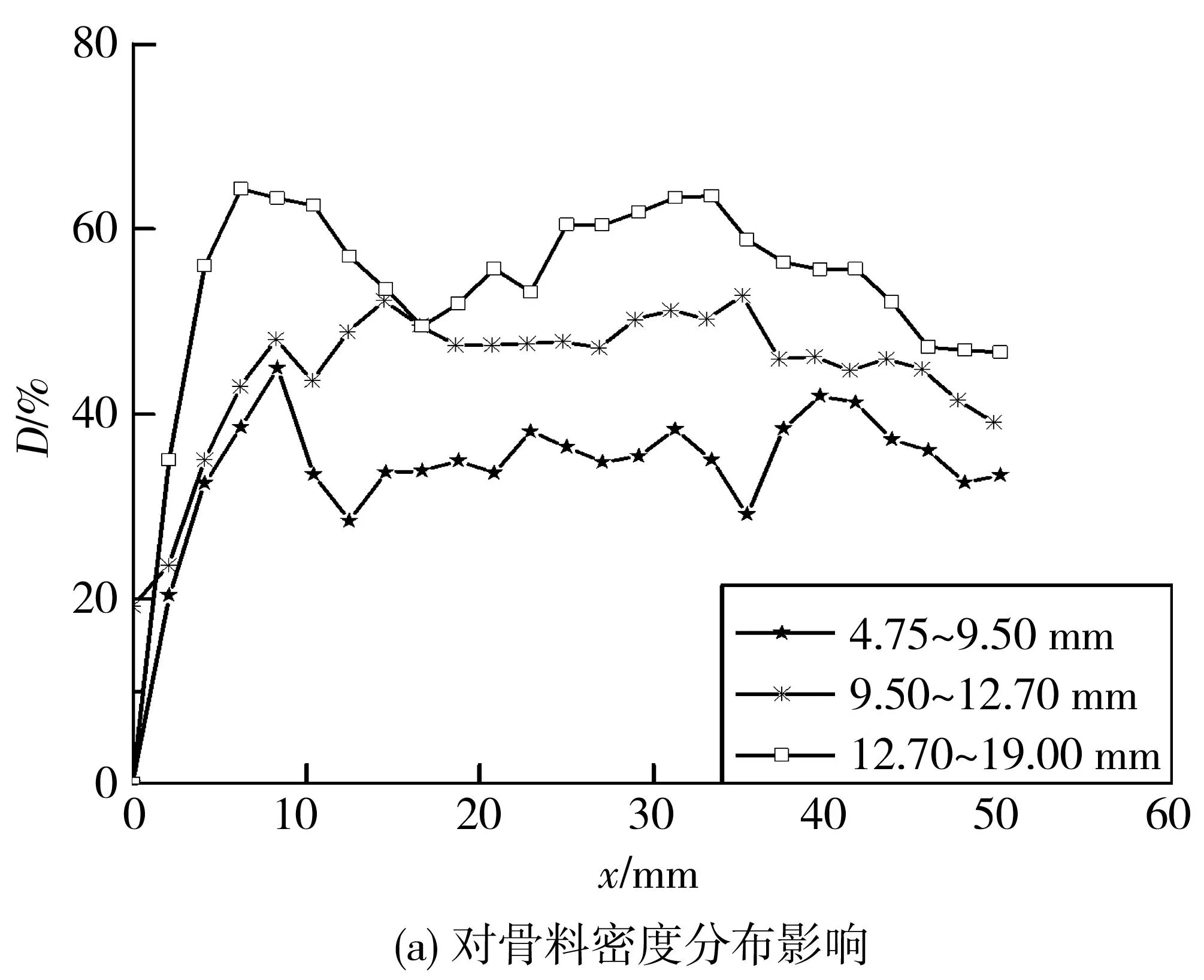
图8 骨料粒径对骨料密度分布曲线的影响Fig. 8 Effect of aggregate particle size on the aggregate density distribution curve

由于样本数较少,每组仅两个试样,这就导致样本结果会出现异常的涨落现象,其离散性较强,无法获得令人满意的统计结果,也无法准确地描述骨料粒径、含量、形状等因素对混凝土边界效应的影响规律。故笔者将继续借助数值模拟技术建立多样本随机骨料模型,通过大量数值模型对混凝土边界效应进行研究。

2.2 再生混凝土随机骨料模型

笔者提出了一种新型的二维骨料建模方法,即骨料压缩建模方法。先将骨料假定为圆形并投放到指定断面内,获得圆形随机骨料模型;随后按照一定压缩比(压缩比为圆形骨料压缩后椭圆形骨料短轴与长轴的比值)对圆形骨料进行压缩并旋转[14],可获得椭圆形随机骨料;进一步在椭圆形骨料几何边界上随机选择并向外扩展,可获得凸多边形随机骨料。

采用文献[15]公式建立一级配再生混凝土二维断面级配曲线,如式(3):

(3)

式中:Pk为骨料体积与混凝土总体积的百分比,一般取Pk=0.75;Pc粒径小于D0的骨料累积分布概率;D0为粒径;Dmax为最大粒径。

以尺寸为100 mm× 200 mm的模型为例,圆形骨料粒径分别为17.5、12.5、7.5 mm,这3种粒径分布如表1。

二维再生混凝土随机骨料模型如图9。在生成随机骨料模型时,可固定骨料长径比为某一具体数值,也可在指定范围内随机生成;当长径比随机变化时,生成的圆形骨料存在交叉,但通过压缩并旋转后,则交叉现象消失;若长径比固定为1时,则圆形骨料不会出现交叉现象;对于凸多边形的表面棱角数量,可固定为某一数值,也可在指定范围内随机生成,此处限定在10～20随机生成某一数值。基于该方法,能建立具有任意长径比的椭圆形及凸多边形骨料几何形态,也能建立具有任意棱角数量的凸多边形骨料几何形态,为系统研究骨料几何形态对边界效应影响分析奠定模型基础。

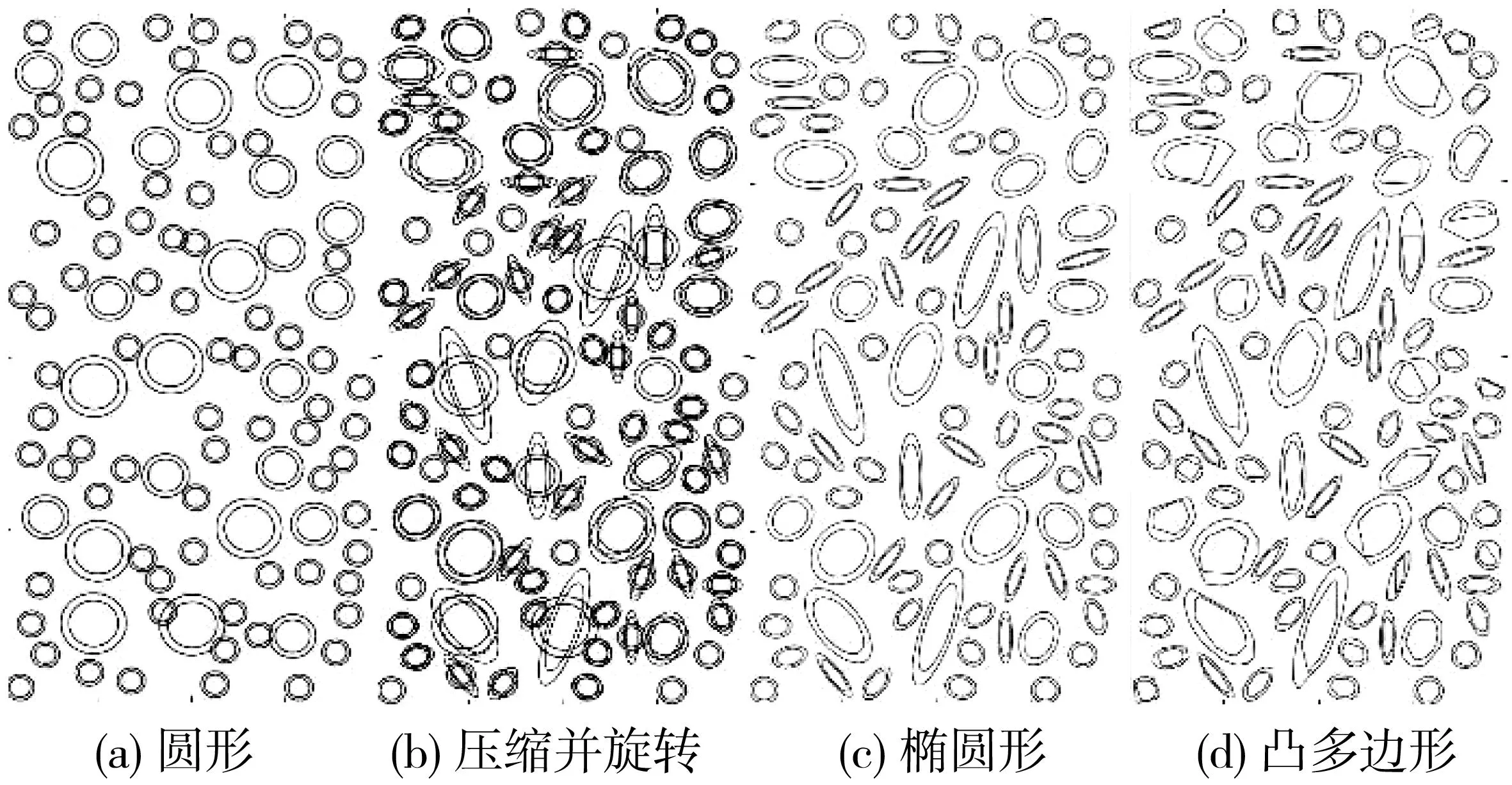
图9 二维再生混凝土随机骨料模型Fig. 9 2D random aggregate model for the recycled concrete

2.3 骨料边界效应

所建立的再生混凝土随机骨料模型尺寸为100 mm× 200 mm,骨料最大粒径为17.5 mm,最小粒径为7.5 mm。

图10为骨料面积百分比为40%时的密度分布随模型数量N变化的规律曲线。由图10可知:当N=1时,中间区域骨料密度波动较大,这说明从单个试件上很难确定混凝土边界效应及影响因素。由于骨料分布的随机性特点,导致模型之间骨料分布具有差异性,故少量模型无法反映边界效应真实情况,特别是中心区域。曲线虽然缺乏明显规律,但在边界效应层范围内,仍然符合实际情况。故笔者建立了1 000个圆形骨料随机模型,并分别统计了N=1、10、20、50、100、500、1 000时的边界效应及骨料密度分布曲线。

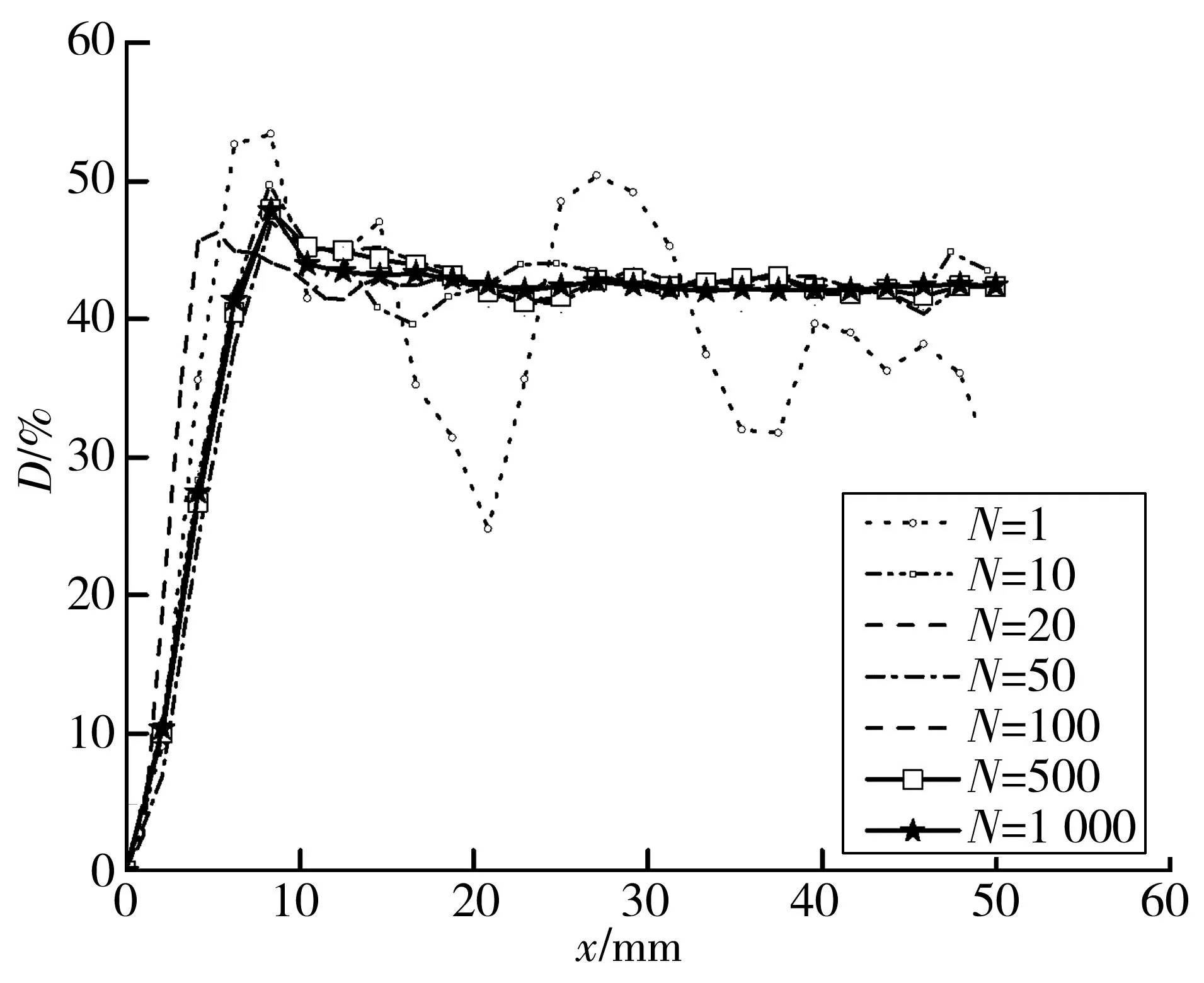
图10 再生骨料密度分布曲线Fig. 10 Density distribution curve of the recycled aggregate

图10中:随着N逐渐增加,试件边界层及中心区域均呈现出比较稳定的变化规律,由上升段、下降段及水平段组成;特别是中心区域,逐渐趋于稳定,发展为一条水平线;骨料密度趋于稳定时的距离则为边界效应层厚度。密度曲线的峰值厚度大致为7.5 mm,等于试件内的最小骨料粒径,而边界层约为12.5 mm,约等于试件内的平均骨料粒径。这主要是由于混凝土在浇筑过程中,由于模板边界影响,振捣过程中大粒径骨料向内部移动,小粒径骨料逐渐迁移到混凝土边界附近,从而导致表面附近的骨料密度高于内部。同时可知,中心区域的骨料密度约为41%～43%,略高于骨料面积百分比,这是由于骨料面积百分比是固定的,由于表面骨料密度较低,中心区域高出的骨料密度补偿了表面区域的骨料密度损失。

2.4 骨料长径比对边界效应影响

圆形骨料是一种比较理想的模型,基于此形状的再生混凝土边界层效应研究虽能反映出一定的规律,但结果与真实混凝土骨料边界效应可能存在一定误差。

通过建立大量椭圆形随机骨料模型,研究了骨料形状对再生混凝土边界效应的影响规律。建立长径比为2.77、1.56、1.00和在1.00～4.00随机分布的4种椭圆形随机骨料模型,模型标记为r,如图11(a)。其中,当长径比为1.00时,骨料为圆形骨料,如图10;不同粒径的骨料边界效应研究结果如图11(b)。

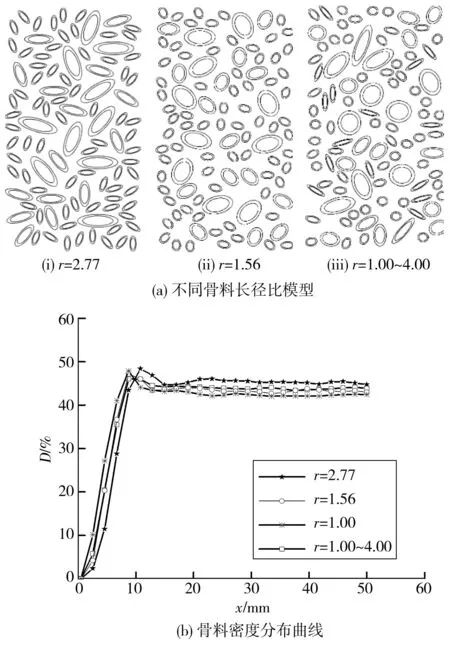
图11 骨料长径比对密度分布曲线的影响Fig. 11 Effect of aggregate length to diameter ratio on the density distribution curve

由图11(b)可知:无论长径比如何变化,骨料密度分布曲线的形状并无明显改变;但随着骨料长径比增加,密度分布曲线的峰值逐渐增加,边界效应层厚度也逐渐增大,与文献[5]结果吻合较好。同时也可发现,长径比对试件中心区域骨料密度具有明显影响,对于高长径比的骨料模型,中心区域骨料密度明显大于低长径比的。造成上述现象的主要原因是:由于随着长径比逐渐增大,骨料存在一定的尖角,而尖角阻碍了骨料在模板附近分布,迫使骨料向中间位置移动,从而进一步增加了边界效应层厚度及中心区域的骨料密度。

混合多种长径比的椭圆形骨料模型与实际骨料吻合度最高,因此该模型骨料密度分布曲线基本可以代表实际的再生混凝土边界效应。由此可知:密度分布曲线峰值对应厚度约为9.0 mm,为最小骨料粒径;边界效应层厚度约为16.5 mm,为椭圆形骨料的平均粒径。

2.5 骨料粒径对边界效应影响

再生混凝土随机骨料模型的形态分为两种:① 内部仅有一种粒径的圆形骨料模型;② 粒径在指定范围内随机变化的椭圆形骨料模型。通过上述模型定量研究了骨料粒径对再生混凝土材料边界效应的影响规律。每种粒径建立样本数量均为1 000,样本总量为6 000,获得的骨料密度曲线如图12。

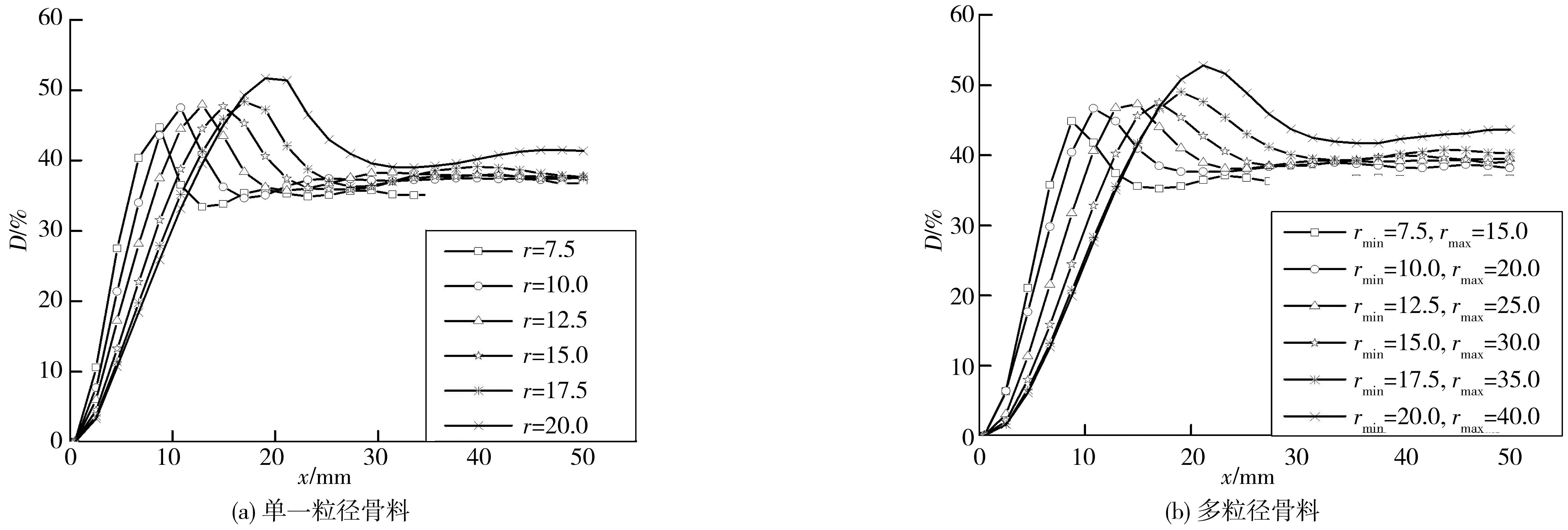
图12 骨料粒径分布对密度分布曲线影响Fig. 12 Effect of aggregate particle size distribution on density distribution curve

由图12可知:由两种骨料模型获得的密度曲线形状并无显著区别;但单一粒径分布的模型边界层厚度明显小于多粒径分布的,这是由于试件内骨料级配不良所造成。

骨料粒径分布对边界效应层的影响如图13。由图13可知:这两种模型的曲线峰值厚度分别为粒径的1.025 1、1.095 5倍,大约对应模型内最小骨料粒径;单一骨料中不存在最大粒径,仅包含一种骨料粒径,边界层厚度约为1.315 1倍的骨料粒径。多粒径骨料模型中边界层厚度约为模型内最小粒径的1.526 8倍,对应的粒径尺寸约为模型内平均骨料粒径。无论对于峰值厚度还是边界层厚度,多粒径骨料模型均大于单一粒径的骨料厚度,这是由于多粒径骨料级配较好,在震动作用下,大粒径骨料逐渐向内部移动,而边界区域填充着大量的小粒径骨料。

图13 骨料粒径分布对边界效应层的影响Fig. 13 Effect of aggregate particle size distribution on boundary effect layer

2.6 骨料棱角对边界效应影响

椭圆形骨料虽能反映卵石类骨料的形态,但无法反映出碎石类骨料的形态特征,特别是碎石骨料表面棱角及凸起等。因此笔者建立了凸型骨料棱角数量分别为10、15、20及随机分布等4种随机骨料模型,研究了凸多边形骨料棱角数量对骨料边界效应的影响,骨料模型如图14,标记为A。为了建立更符合实际的骨料形态,所建立的模型中骨料长径比在1.0～4.0随机分布。

图14 不同棱角数量的凸多边形随机骨料模型Fig. 14 A convex polygon random aggregate model with different numbers of edges and corners

每种骨料建立500个样本,共计2 000个样本,获得的骨料密度分布曲线如图15。当凸多边形表面骨料棱角数量较小及棱角数量随机分布时,棱角数量对骨料密度分布曲线几乎没有影响;当棱角数量较多时,边界效应层厚度略有增加。这是由于骨料表面棱角数量较多时,骨料形态更接近于圆形或椭圆形,骨料在试件内分布受到其他骨料尖角的影响较小,模板边界附近的骨料向内部迁移的阻力减小,因此试件中心区域骨料含量略有增加。

图15 不同棱角数量的骨料密度分布曲线Fig. 15 Density distribution curves of aggregates with different numbers of edges and corners

3 结 论

笔者基于图像识别技术获得了具有真实再生骨料特征分布的细观结构模型,并借助随机骨料建模技术建立了圆形、椭圆形及凸多边形等具有多种几何形态特征的随机再生骨料模型;通过上述模型研究了骨料边界效应,获得了骨料密度分布曲线;建立大量数值模型研究了骨料长径比、骨料粒径及骨料表面棱角等几何特征对骨料密度分布曲线、骨料峰值密度厚度及骨料效应层厚度影响规律,获得结论如下:

1)随着边界距离增大,骨料密度分布曲线呈现上升、下降、最终趋于稳定形态,最终稳定段的骨料密度略大于试件内的;曲线形态特征不受骨料形状、粒径、长径比、表面特征等几何形态影响;

2)骨料密度曲线峰值对应的边界距离约为最小骨料粒径,边界效应层厚度约为平均骨料粒径,且均随着骨料粒径和骨料长径比增加逐渐增加。骨料级配对骨料边界效应层厚度具有显著影响,但对骨料密度峰值厚度的影响基本可忽略;

3)由于模板边界影响,大粒径骨料逐渐向内部移动,而小粒径骨料逐渐迁移到试件模板边界附近,造成边界区域骨料密度较小,而中心区域骨料密度较高,中心区域高出的骨料密度补偿了表面区域的损失;

4)在骨料形状、长径比、粒径及表面棱角等几何特征中,骨料最大粒径及最小粒径对效应层厚度、骨料密度峰值厚度的影响最为强烈,而骨料形状和骨料表面棱角等特征的影响相对较小;

5)骨料边界效应同时受到骨料形状、长径比、粒径及表面棱角等多种因素影响。故在再生混凝土配合设计时,应根据破碎后再生骨料粒径调整颗粒分布以获得最优的骨料级配曲线,从而降低骨料边界效应影响程度。