基于位姿变化的钻铆机器人刚度优化

王明海，张威，刘香辰

(1.沈阳航空航天大学机电工程学院，辽宁沈阳 110136；2.沈阳航空航天大学航空制造工艺数字化国防重点学科实验室，辽宁沈阳 110136；3.沈阳航空航天大学航空宇航学院，辽宁沈阳 110136)

0 前言

近年来，机械臂制孔在航空工业领域的应用越来越普遍，随着机器人技术的不断进步，对其加工精度也提出了更高的要求。然而工业机器人固有的弱刚性却严重阻碍了行业的发展，故提升其作业刚度、保证工件加工质量很必要。针对此问题，国内外学者已经在工业机器人刚性方面做过相关探索，CVITANIC等[1]利用静态和动态刚度模型对不同切割场景下的机器人姿态优化进行了比较研究，结果表明优化可减少执行器偏转，但不能使其回落到可重复性范围内。华中科技大学的杨靖等人[2]提出一种对铣削机器人主刚度定向的方法，深入研究机械臂的冗余度，改进加工位姿以减少铣削过程的颤振。XIONG等[3]提出机械臂冗余度，采用离散搜索方法将五轴刀具数控路径转换为六轴工业机器人轨迹进行优化。陈钦韬等[4]将铣削力椭圆平面的各向同性度作为评价指标，运用遗传算法进行位姿优化，使被加工件铣削平面度提升45%。诸多学者对工业机器人奇异问题、刚度辨识、误差补偿等都进行了相关理论研究，但针对钻铆机器人实际工况下刚度优化探索较少。本文作者以位姿的调整为切入点，结合实际，利用改进后的智能优化算法，对串联机器人重载下的整体刚度进行深入研究，并证实了其有效性。

1 机器人运动学建模

1.1 运动学模型

工业机器人运动学模型可以清晰表示工业机器人加工时所处位姿，反映机械臂连杆间的几何关系。本文作者以KUKA KR600 R2830型工业机器人为例进行研究，该型号机器人本体质量约2 650 kg，额定负载为6 000 N，负载高、工作范围大，姿态重复精确度可达±0.08 mm，使其适用于高精密、大负载条件下制孔加工任务。机器人整体结构由6个旋转关节串联而成，称为串联工业六自由度机器人，可以采用改进的D-H法[5]来建立机器人运动学正解，对机器人参数化。图1所示为机器人在进行板类部件钻铆作业时的场景。

图1 工业机器人钻铆

依照工业机器人作业位姿在其关节连接部位创建笛卡尔坐标系，根据连杆数据建立运动学数学模型，如图2所示。参数见表1。

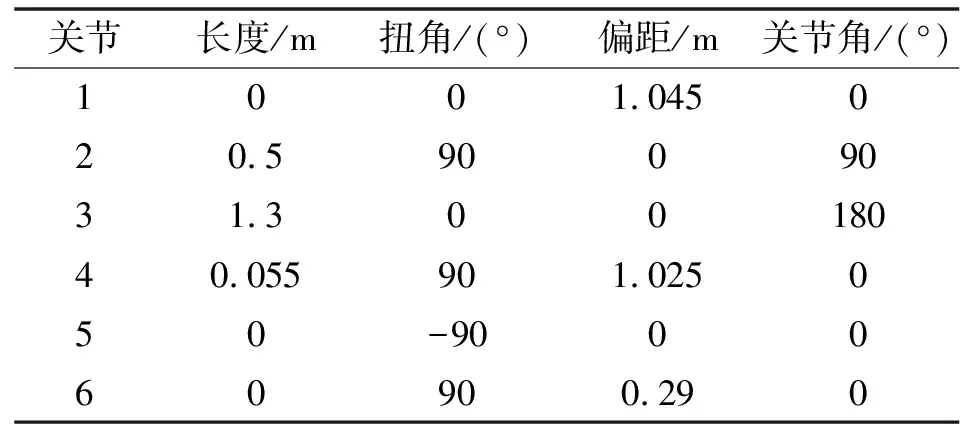
表1 机器人D-H参数

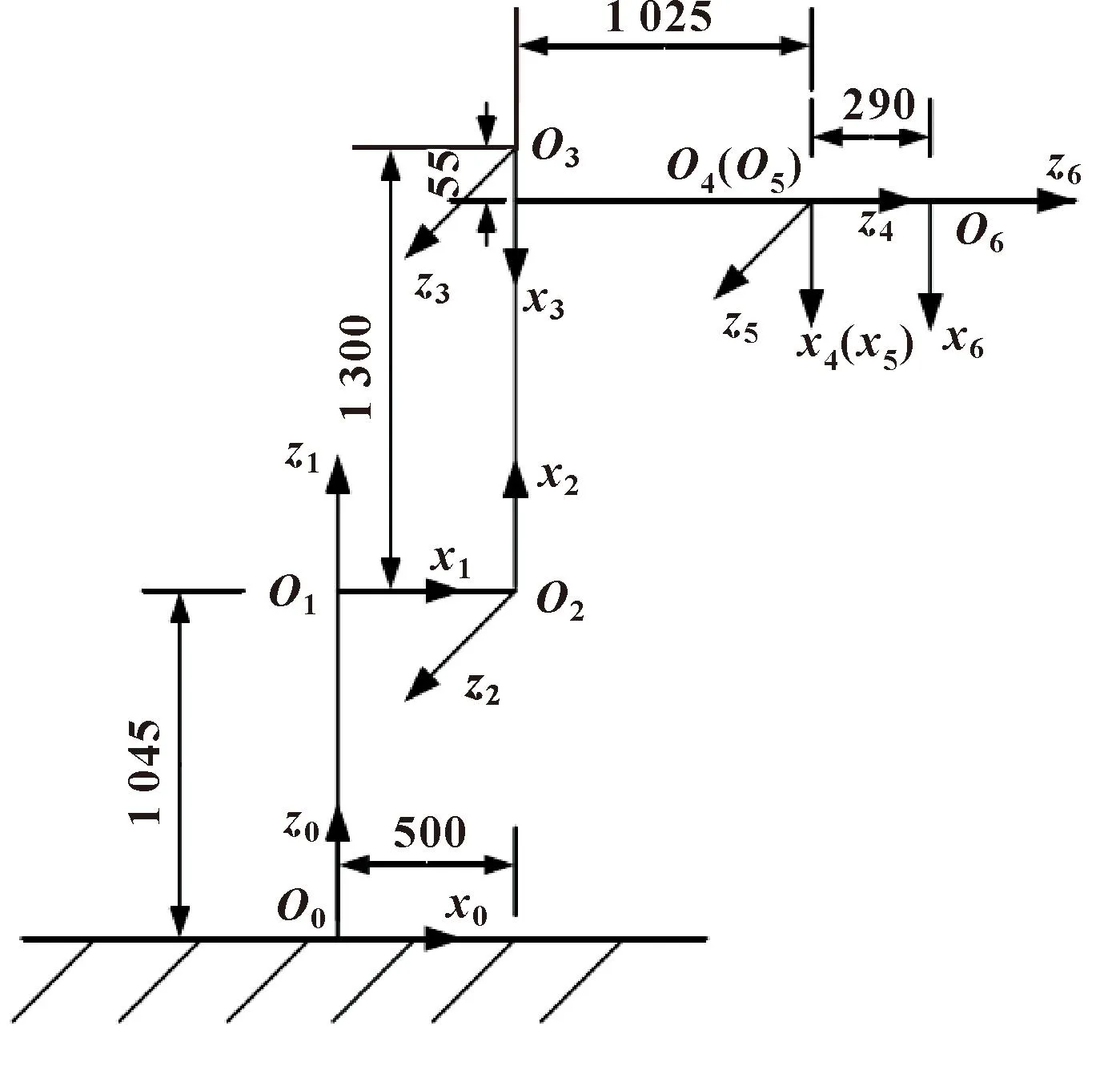
图2 运动学模型

模型中的4个关键参数为ai-1、αi-1、di和θi，分别是连杆长度、连杆扭转角、连杆偏距和关节角。坐标系{i}可以由坐标系{i-1}经过4次旋转或平移运动变换得到，将4步转换矩阵连乘可以获得两相邻连杆间的变换关系，可写为

i-1iT=R(X，αi-1)T(X，αi-1)R(Z，θi)

T(Z，di)=

(1)

1.2 雅可比矩阵

雅可比矩阵的数学意义是表示从机器人关节速度到机器人末端操作速度的一种映射关系[6]，需要注意的是该广义传动比非定值。雅可比矩阵的求解方法通常有矢量积法[7]和微分变换法，本文作者通过对比两种方式编程及结果的复杂度优先选用矢量积法进行计算。假设机器人末端线速度和角速度分别用v和ω表示，则关节速度与末端速度的关系如式(2)所示：

(2)

(3)

综上得到KUKA机器人的雅可比矩阵公式为

(4)

由公式(4)可以在MATLAB中编程求解R2830型机器人雅可比矩阵。

2 机器人刚度性能分析

2.1 刚度模型

刚度反映的是机械臂在外力作用下抵抗变形的能力，关节刚度、连杆刚度以及所处位姿都影响机器人末端操作刚度[8]。在大负载条件下，由连杆变形所造成的末端变形远小于关节所造成的末端变形，为简化计算可将机器人连杆视为刚性，在此条件下机械臂末端操作刚度仅与各关节刚度和所处位姿相关。在这一假设下，讨论机器人关节刚度与末端操作刚度之间的关系，讨论机器人末端变形与末端受力之间的关系，建立数学模型，从而得到机器人的末端操作刚度模型为

F=J-TKθJ-1X

(5)

其中：F为末端力矢量；J为雅可比矩阵；Kθ为关节刚度矩阵；X为末端变形矢量。将式(5)变形处理可得：

(6)

整理后得：

(7)

2.2 机器人关节刚度辨识

针对工业机器人关节刚度获取，主要有以下两种方法：(1)通过对关节处伺服电机、减速器等部件的结构、材料、规格等数据进行计算[9]，求其等效刚度值。(2)设计关节刚度辨识实验[10]，处理实验数据计算刚度值。其中方法一过于理想化，机器人关节部件的各项参数很难获得且计算繁琐，故选择方法二求解工业机器人关节刚度。

式(6)为关节刚度识别实验的原理，加工时由扭矩造成的旋转位移较小，可忽略不计，故辨识实验只取变形的前3项即末端平移位移[dx，dy，dz]T进行计算[11]。辨识实验所搭建的实验平台如图3所示，其中激光跟踪仪型号为Radian Core(50)，测力仪为瑞士KISTLER及配套Dynoware软件。实验中激光跟踪仪和测力仪所测得的数据均是在自身坐标系原点处，故先将激光跟踪仪坐标系转换至机器人基坐标系下，测力仪还需二次转换至机器人末端法兰中心处进行标定。

图3 关节刚度辨识实验平台

通过测量工业机器人在多个位姿时的末端变形及力矢量代入式(7)，利用最小二乘法[12]在MATLAB中进行编程可以求得机器人关节刚度矩阵Kθ。求解出的工业机器人各关节刚度如表2所示。

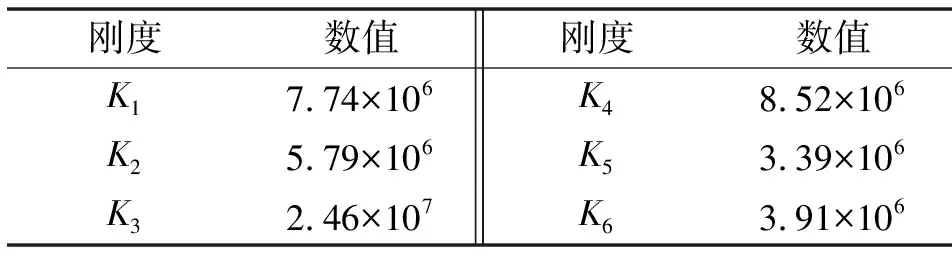
表2 工业机器人关节刚度 单位：N·m·rad-1

3 基于位姿的刚度性能优化

3.1 刚度性能评价指标

机器人末端操作刚度Kx为六阶矩阵，是一张量测度[13]，故需一准确值来表述机器人末端的刚度特性。工业机器人刚度性能评价指标[14]有3种，分别是矩阵瑞利熵、变形椭球(刚度椭球)和力椭球(柔度椭球)[14]。在使用力椭球进行计算时，无需计算雅可比矩阵的逆，计算较为简便且易编程，故选择力椭球作为刚度性能评价指标。将式(5)展开并经变形处理可得：

(8)

由于机器人末端在外力下的扭转变形量远小于位移变形量且无法精确测得，故省略扭转变形[15]，将δ设为0，由式(8)可得：

d=cfd·f

(9)

其中：

cfd=

(10)

假设机械臂法兰端受到外力作用时造成单位变形，即d=1，可得：

(11)

通过分析可知，式(11)表示一椭球体，其方程可以写为

(12)

借助蒙特卡洛法可以求解工业机器人的工作空间及空间内的刚度性能[16]，原理是利用机器人末端所能达到所有点的集合来表征机器人可达空间，如图4所示。

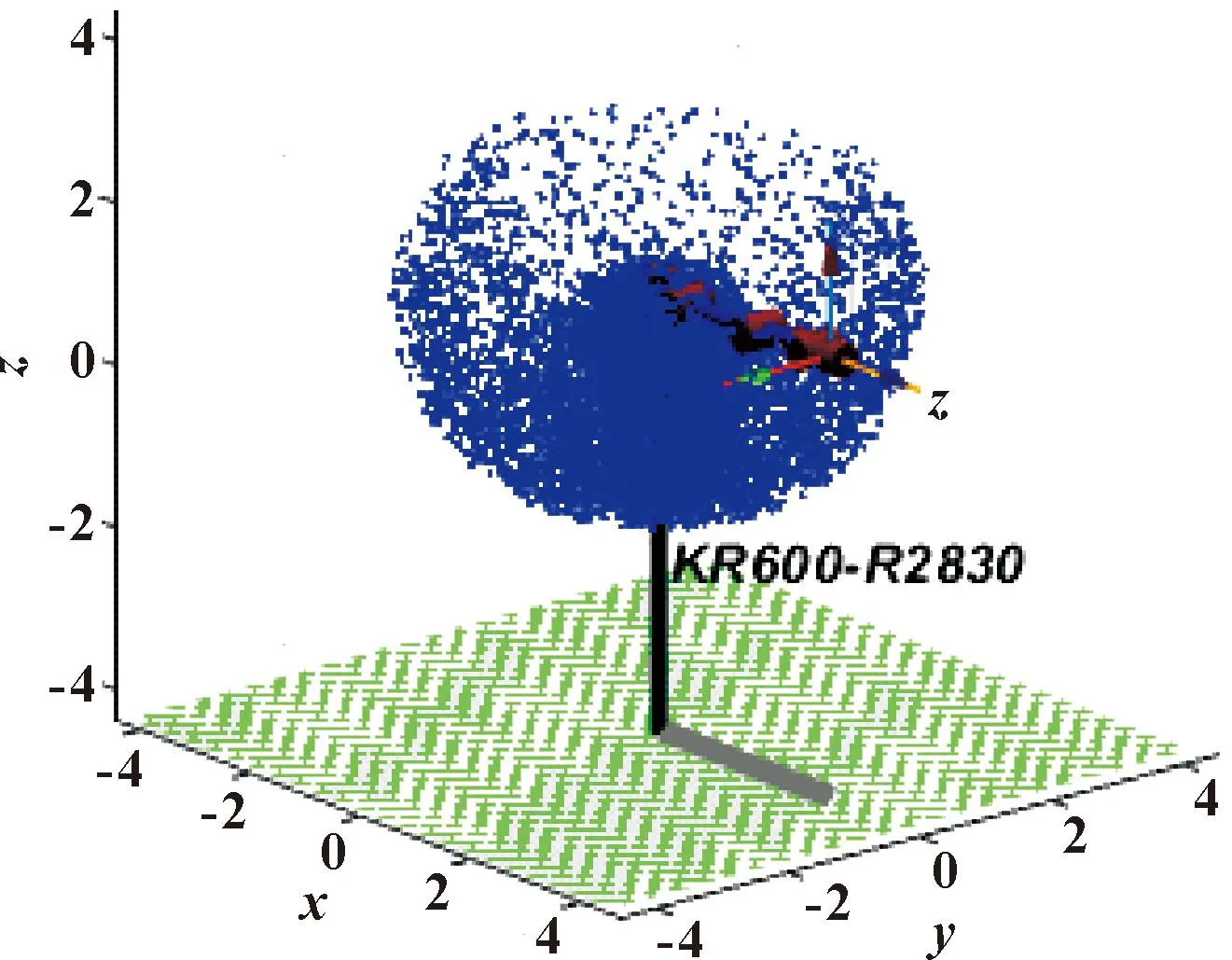
图4 机器人工作空间云图

结合柔度矩阵及刚度性能评价指标，在MATLAB中编程仿真可以得到机器人工作空间刚度性能云图如图5所示，图中蓝色较深区域工业机器人刚度性能指标较优，故所处位姿末端刚度较高，故机器人在加工时应尽量选择末端处于蓝色区域的位姿进行加工。

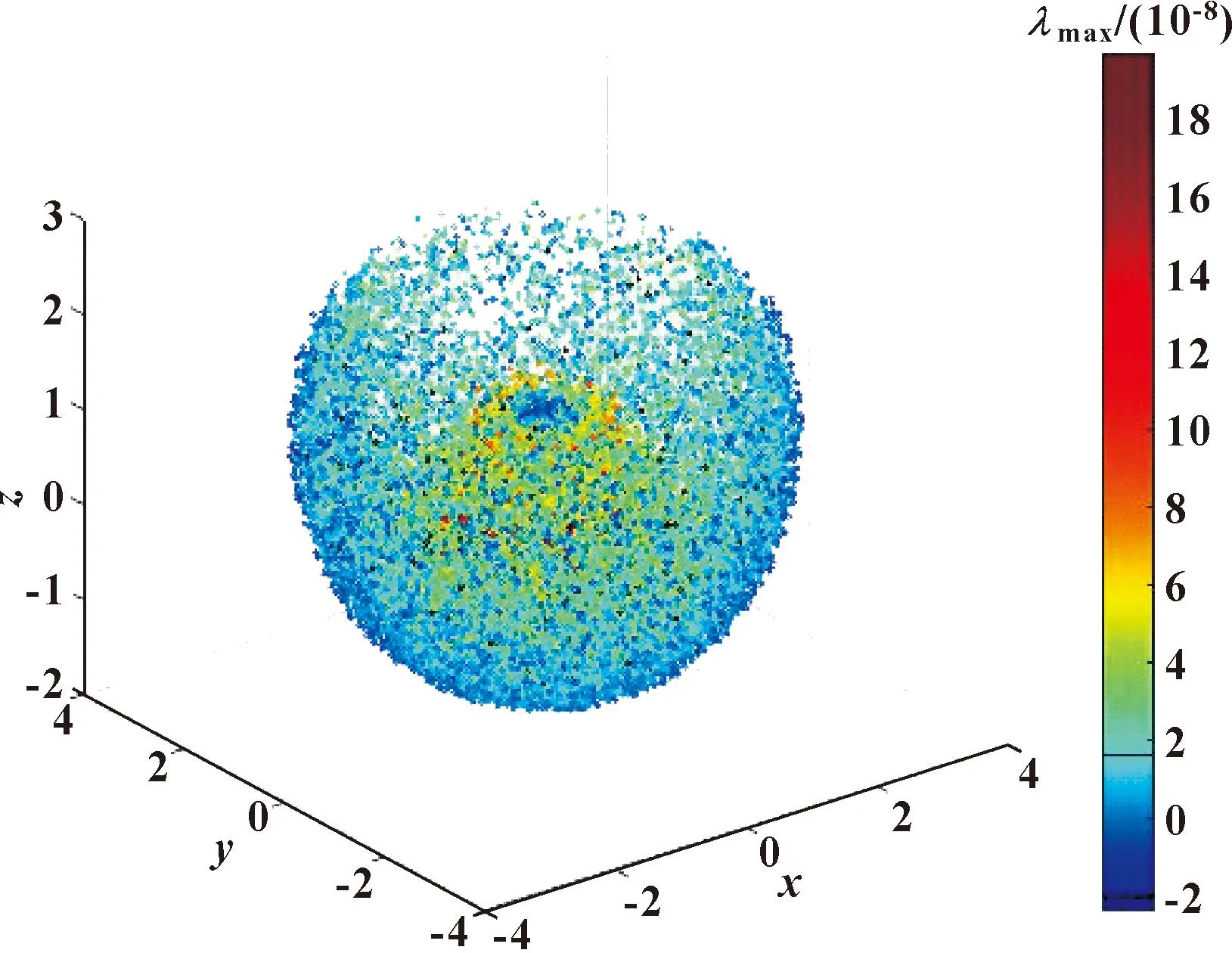
图5 刚度性能云图(xOz向)

3.2 算法优化模型

寻求最优解即求函数极值的问题，重点在于3个关键条件的建立，即数学模型的目标函数、设计变量及约束条件。下面以工业机器人作业时刚度性能最大化为目标建立数学模型，解决此优化问题的基本思想是通过整个可达空间中各个位姿之间的协作和信息共享来寻找最优位姿。选用粒子群算法的原因在于其思想简单，求解过程迅速。建立目标函数时，选择柔度矩阵cfd的最大特征值λmax作为刚度性能评价指标k，λmax的值越小，机器人末端产生单位变形所需最小外力越大，机器人刚度性能越好，反之刚度性能越差。

机器人所处位姿与关节角度相关，故变量为关节角θ。其中θ1及θ6对工业机器人末端操作刚度无影响[17]，θ2及θ3主要影响机械臂末端位置，θ4及θ5主要影响末端方向。在自动化钻铆系统中，工业机器人多配备滑轨进行作业，θ4对末端位置及方向的影响可以通过机械臂在滑轨上的平移替代。由此粒子群优化算法中自变量的个数可以减少为3个，可加快算法求解速度。

将关节角上下限作为界限约束，规定变量取值范围。实际工况下机械臂末端刀具顶点C需与工件作业点P重合，令点C在基坐标系{B}中的表达为[Cx，Cy，Cz]T，点P在基坐标系{B}中的表达为[Px，Py，Pz]T，则需保证：

ΔH1=(Cx-Px)2+(Cy-Py)2+(Cz-Pz)2

(13)

其次刀具轴线与目标点法方向需一致，故刀具坐标系{C}相对于基坐标系{B}与目标点坐标系{P}相对于基坐标系{B}的位姿偏差[Δax，Δay，Δaz]T为0，如下：

ΔH2=(Δax)2+(Δay)2+(Δaz)2

(14)

故可将工作中末端姿态偏差H(θ)作为性态约束，可得机器人数学模型为

(15)

3.3 优化算法

粒子群算法(PSO)操作简单、收敛速度快，在函数优化中全局最优解搜索能力较强，故选择粒子群算法进行计算。算法具体流程如图6所示。

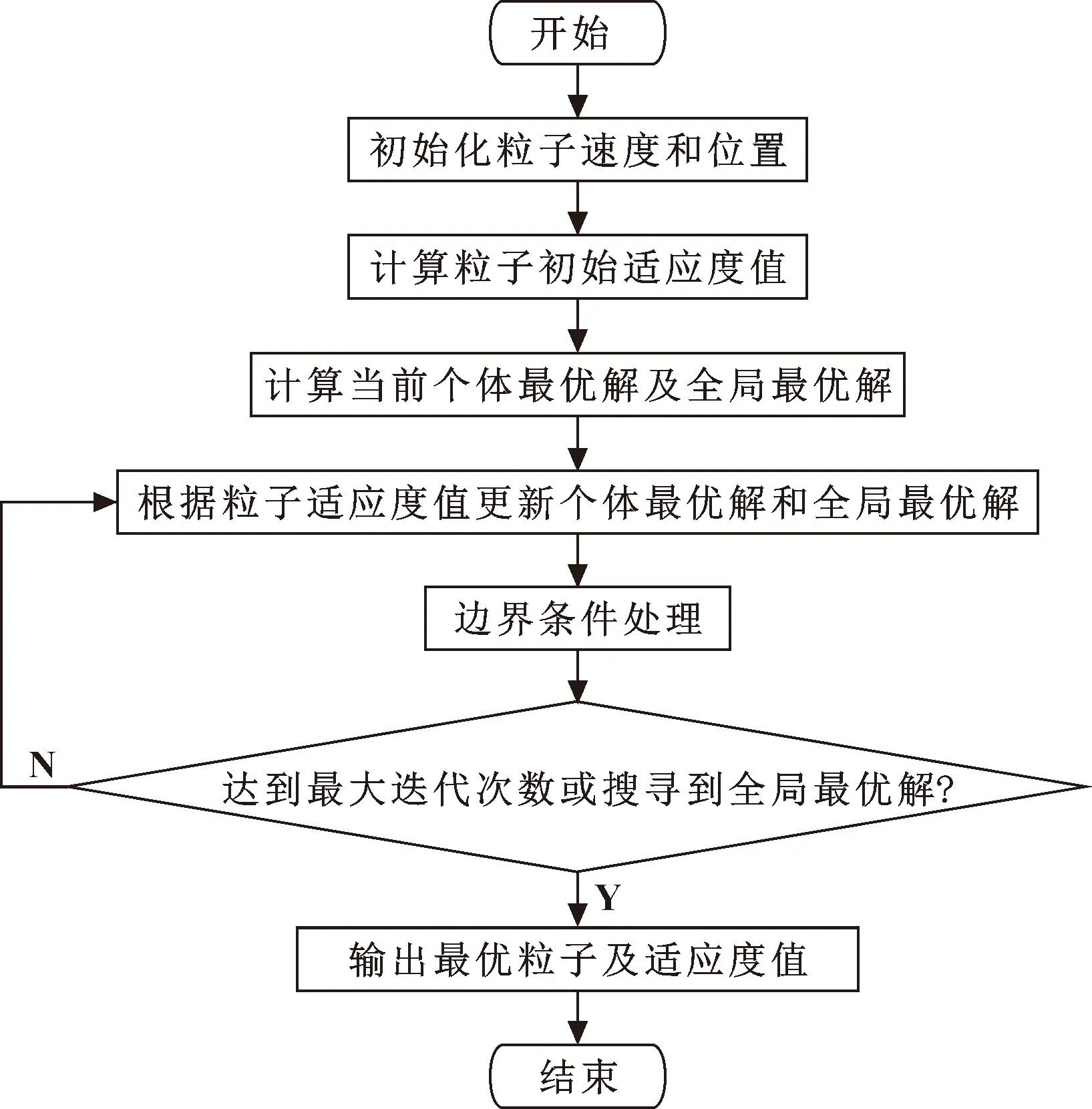
图6 粒子群算法流程

优化参数中迭代次数设为1 000，自变量个数n=3，设置群体粒子个数N=100并随机初始化每个个体的速度和位置。定义适应度函数，个体极值是第i个粒子搜寻到的最优位置，全部个体极值的最优解为此次全局最优解，结果与历史全局最优解进行比对，然后更新。此次计算ω取0.8，C1和C2取2。粒子速度、位置迭代的公式为

v(i+1)i=ωvid+C1rand(0,1)(Pid-xid)+C2rand(0,1)(Pgd-xid)

(16)

x(i+1)d=xid+vid

(17)

3.4 优化结果

设计好算法相关参数和流程后，可以在MATLAB中编写程序求解，最终得到最优位姿。为了验证优化结果的正确性，参照工业机器人钻铆作业实况，随机选取一组机器人关节角结合上述优化算法进行求解，得到优化后的工业机器人加工位姿(关节角配置)，迭代结果如图7所示。

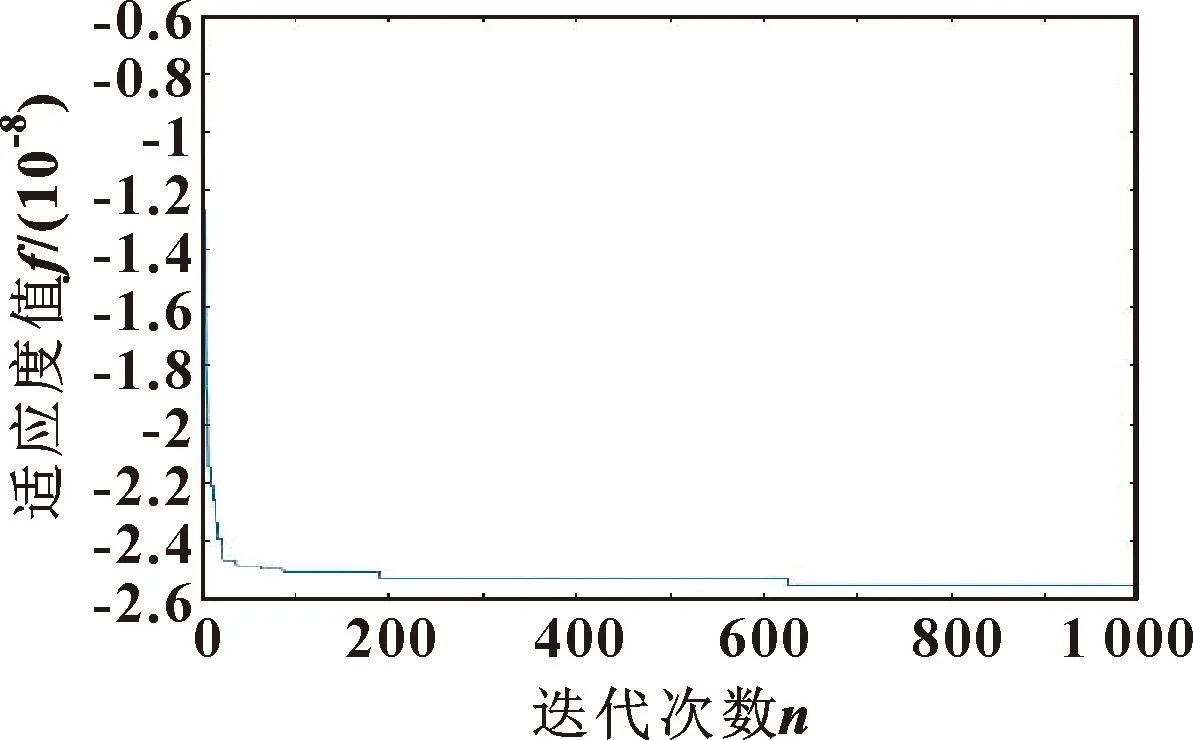
图7 位姿优化迭代过程

根据钻铆工业机器人实际工况随机选择一组关节角(见表3)与算法优化后的关节角进行末端理论变形量的对比，将两组关节角分别代入式(9)并假设在末端施加z轴方向的力F=100～1 100 N，图8为优化前后末端变形量的对比。可以发现：优化后的末端变形量更小，效果明显，优化程度在60%以上且精度可以控制在0.03 mm以内，验证了改变加工位姿对提升工业机器人末端刚度的有效性，且可使加工孔位精度小于0.5 mm，法向精度小于0.5°，满足了飞机对制孔位置的要求。

表3 优化前后关节角及刚度参数

图8 位姿优化前、后变形量

由表3可知KUKA KR600 R2830型串联机械臂刚度最大时关节角的准确值，可为机器人作业时加工位姿的选择提供参考。在SolidWorks中绘制工业机器人模型并导出到MATLAB中，可清晰表达工业机器人刚度最优的位姿，如图9所示。

4 结论

通过对六自由度机械手进行运动学分析、工作空间分析及刚度分析，采用参数优化后的粒子群算法来寻找机器人刚度最大的加工位姿，减小机械臂末端变形，优化机器人的加工质量，保证工业机器人在高精度、大负载条件下的加工刚度，而且考虑实际工况改良的优化方法适用于同类型各种型号的串联机器人。在航空航天部件钻铆加工中，面对配备大负载末端执行器或加工合金或复合材料工况时，通过调整工业机器人的位姿来提高刚度，满足加工精度要求，既节省资源又有良好的优化作用。其中的分析过程可为后续研究提供基础。