基于SARIMA 和SVR 组合模型的转向架系统寿命评估

师 蔚，范 乔，杨 洋，胡定玉，廖爱华

（1 上海工程技术大学 城市轨道交通学院，上海 201620；2 上海地铁维护有限公司 车辆分公司，上海 200031）

随着我国经济的快速发展，地铁成为人们出行的主要交通工具，转向架作为地铁车辆的重要组成部分，其性能对车辆运行的稳定性和安全性有重要影响。基于安全性的考虑，对地铁车辆转向架系统进行健康状态和剩余寿命评估，有助于针对性地制定检修、退役或延寿方案，对城市轨道列车运营的安全性与经济性均具有重要意义。

车辆转向架属于机械系统，目前机械系统的寿命评估预测方法主要有基于模型的预测和数据驱动的预测方式两种［1］。其中基于模型的方法是指利用模型对系统剩余寿命进行预测，目前转向架系统的寿命预测大多是基于动力学模型［2-3］，如有限元分析模型对转向架零部件的寿命预测分析，但很少有基于故障数据对转向架整体进行寿命评估分析。数据驱动主要指基于故障数据采用机器学习方法进行寿命预测，主要方法包括神经网络［4］、支持向量机等。但单个预测模型难以满足数据多样复杂化的条件，一般将支持向量机和其他模型或算法结合，以提高预测精度。Chen 将相似性理论和SVM 模型结合，对发动机的寿命进行预测，验证了模型的有效性［5］。刘珍翔提出了改进增量SVR 模型对齿轮寿命进行预测，并验证了该模型更可靠稳定［6］。NIETO 等为提高预测精度，采用粒子群优化SVM 模型对航天发动机进行寿命预测，解决了训练时超参数的优化问题［7］。但车辆转向架系统属于可修复系统，其故障数据因维修计划存在一定的周期性，因此需结合具有周期性的预测模型，以适应转向架故障数据特征的需要，建立更优的组合预测模型。

文中建立基于地铁车辆转向架系统历史故障数据的健康指数，将具有周期性的SARIMA 模型和SVR 模型进行组合，同时采用协方差优选法将二者的权重进行分配，预测转向架系统的健康指数，最后将历史和预测的健康指数结合后，建立与运行时间的数学模型，分析得到转向架系统的剩余寿命。

1 转向架系统健康指数及剩余寿命评估

文中依据转向架系统未来的健康状态估计其剩余寿命，选用健康指数HI作为评价其健康状态的指标，HI越大表示转向架系统的健康程度越高，反之健康程度越低，计算公式为式（1）［8-9］：

式中：K为比例系数；C为曲率系数；λ（t）为转向架系统的故障率，故障率为式（2）：

式中：dN（t）为［t，t+dt］内发生故障的次数；当dt趋于0 时，λ（t）为瞬时故障率；当dt为一段时间时，λ（t）为这段时间内的平均故障率。

当健康指数HI下降到转向架允许的最低值时，表明转向架已达到最大使用年限，不能再继续使用，其所对应的时间为转向架的总寿命T0为式（3）：

式中：HIL为转向架所允许的最低健康指数，文中设定为70。由此可得转向架系统的剩余寿命ΔT为式（4）：

式中：T1为转向架的已使用年限。

因此，根据转向架的历史健康指数对其未来健康指数进行预测，并建立历史健康指数和预测的健康指数HI与运行时间T的数学模型，利用式（3）和式（4）估计转向架剩余寿命。

2 基于SARIMA 和SVR 组合预测模型

文中基于转向架历史的健康指数预测其未来值时，转向架系统属于可修复系统，其故障数据因维修计划存在一定的周期性，因此需结合具有周期性的SARIMA 预测模型，以适应转向架故障数据特征的需要，由于单一预测模型的精度和稳定性不高，提出基于SARIMA 和SVR 的组合预测模型，采用协方差优选法确定2 个模型的权重再进行组合，建立更优的组合预测模型。

2.1 SARIMA 预测模型

SARIMA 是常见的时间序列预测方法，由差分自回归移动平均模型演变而来，主要用于分析具有周期性变化的时间序列［10］。

SARIMA（p，d，q）（P，D，Q）S季节性回归移动平均模型可表示为式（5）：

式中：p、q、P、Q分别为非季节和季节性的自回归阶数、移动平均阶数；φ(B)为非季节自回归特征多项式；Ф（BS）为季节自回归特征多项式；θ（B）为非季节移动平均特征多项式；Θ（BS）为季节移动平均特征多项式；（1-B）d为d阶差分；（1-BS）D为D阶季节差分，二者可将时间序列Yt变成平稳时间序列。εt为白色噪声，服从均值为0 且方差为常数的正态分布；BS为季节后移算 子；S为周期；c为 常数；下标t为时刻；γ1，γ2，…，γP为自回归系数；η1，η2，…，ηQ为移动平均系数。

2.2 SVR 预测模型

支持向量机是通过寻找一个最优超平面，使样本所有个体到该平面的几何间隔最大，反之其间隔最小就可寻找一个回归面，即支持向量回归［11］。

SVR 回归估计函数表达式为式（6）：

式中：w为特征空间的维数；φ(x)为从低维到高维的映射；b为偏置项。最优化问题表述为式（7）：

式中：ε为不敏感因子；ξi，为松弛变量；C′为惩罚参数。为求解式（7），引入拉格朗日乘数法得式（8）：

式中：K(xi，xj)=φ(xi)φ(xj)为核函数。文中选用径向基（Radial Basis Function，RBF）核函数为式（9）：

式中：σ0为核宽度。

2.3 SARIMA 和SVR 组合预测

组合预测是利用不同的单个模型预测，并选取适当的权重进行加权，可消除单个预测模型可能存在的偏差，提高预测精度［12］，其模型组合预测值为式（10），组合预测流程如图1 所示。

图1 组合预测模型流程图

式 中：YSARIMA和YSVR分别为SARIMA 预测模型和SVR 预测模型的预测结果；ω1、ω2分别为SARIMA模型和SVR 模型在组合预测中所占权重。

合理有效的权重分配，可提高组合预测的准确性。文中选用协方差优选法，根据误差的方差来确定单个预测模型的权重，当误差的方差大时，其所占权重小，反之其所占权重大。令SARIMA、SVR、组合模型预测的误差分别为e1、e2、e3。SARIMA 和SVR 预测误差的方差分别为σ1、σ2。则组合模型预测误差的方差为式（11）：

用拉格朗日乘数法求var（e3）极小值，在ω1+ω2=1 的条件下，得到SARIMA 模型和SVR 模型的权重为式（12）：

3 应用分析

文中以某地铁运营公司提供的转向架系统故障数据为基础，对健康状态和寿命进行评估，首先统计转向架系统的历史故障率，并转化为对应的健康指数。然后依据历史健康指数，基于SARIMA和SVR 模型分别对健康指数进行预测，并采用协方差优选法得到组合模型中各自的权重，基于权重进行组合得到组合模型预测的健康指数。最后将实际健康指数值和组合预测结果结合，建立健康指数和运行时间的数学模型，当健康指数下降到转向架允许的最低值时，所对应的时间为转向架系统的总寿命，以此得到其剩余寿命。

3.1 转向架系统健康指数

（1）转向架系统故障率仿真

文中统计了转向架系统从开始运营到2021 年7 月的故障数据，以2 个月为时间单位，通过式（2）得到该系统故障率如图2 所示，图中5 个虚线部分分别表示第1 次架修、第1 次大修、第2 次架修、第2 次大修和第3 次架修。

图2 转向架系统故障率

（2）转向架系统健康指数

通过转向架最小故障率来获得故障率和健康指数的转换关系［13］，具体为：当故障率为最小故障率λmin时，健康指数HI=100。由图2 可知，165 个数据点中最小的故障率为0.006 9。采用威布尔分布分段拟合图2 转向架系统的故障率，根据转向架30年的理论寿命，得出健康指数为70 时，故障率为0.192。即λmin=0.006 9，HI=100；λ0=0.192，HI=70；代入式（1），得比例系数K=0.006 9，曲率系数C=0.11。将求得K和C代入式（1），将图2 的故障率转化为健康指数，如图3 所示。

图3 转向架系统健康指数

从图3 看出转向架系统经过架大修后健康指数逐渐降低，健康指数随维修计划存在一定的周期性，因此预测其未来健康指数时，文中采用具有周期性的SARIMA 预测模型，但单一预测模型的预测精度和稳定性不高，文中将SARIMA 和SVR模型进行组合，同时采用协方差优选法确定两个模型的权重，得到更精确的组合预测模型。

3.2 转向架健康指数预测

3.2.1 SARIMA 预测

（1）ADF 平稳性检验

SARIMA 预测的前提是要求数据为平稳序列，通过ADF 检验判定原序列的平稳性，见表1。

表1 ADF 平稳性检验

ADF 检验结果表明，统计量-0.435，大于3 个临界值，说明原序列不平稳，需进行差分运算，一阶差分后统计量为-20.201 8，小于3 个临界值，则一阶差分后序列平稳，d值为1。地铁车辆架大修周期约为4～5 年，即约为48～60 个月进行一次架大修，上述数据均为每两个月统计1 次，因此周期S取25。同理对序列进行周期为25 的一阶季节差分后该序列是平稳的，因此d值取1。

（2）参数值确定

AIC信息准则用来确定模型参数，选取最小AIC值作为最优模型，见表2，AIC=976.533 最小，因此自回归AR 的参数p取2，移动平均模型MA 的参数q取2 时。本数据的自相关与偏自相关系数显著不为0，p、q取值为1。

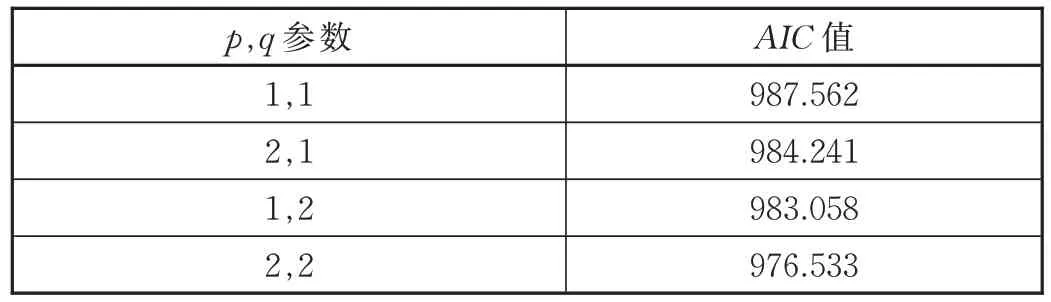
表2 不同参数对应AIC 值

综上SARIMA 模型SARIMA（p，d，q）（P，D，Q）S可确定为SARIMA（2，1，2）（1，1，1）25。

（3）模型残差检验

利用SARIMA 模型预测前，需对模型残差进行检验，如图4 所示，图中残差的有序分布基本遵循正态分布采样的线性趋势，认为上述模型可行。

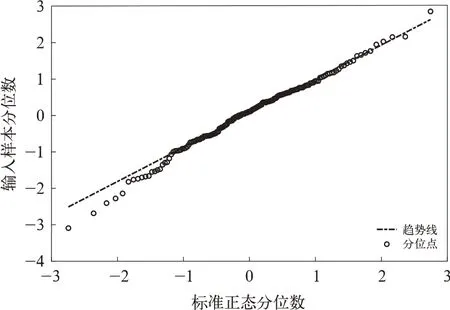
图4 残差检验图

（4）预测结果

文中训练集为1993 年06 月～2016 年10 月转向架的健康指数，测试集为2016 年11 月～2021 年07月数据，测试集预测结果如图5 所示，误差的方差为9.397。并往后进行预测，预测结果如图6所示。

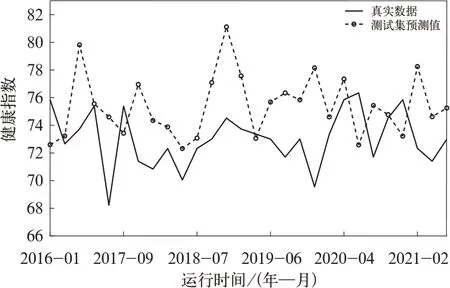
图5 SARIMA 测试集预测值和真实值对比图

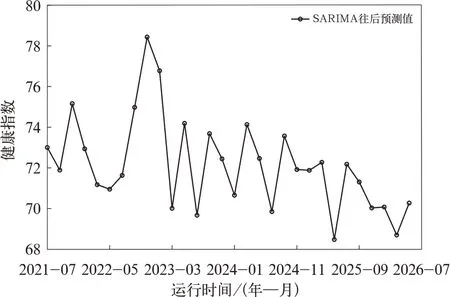
图6 SARIMA 往后预测结果

3.2.2 SVR 预测

（1）数据划分

文中采用交叉和渐消记忆原理将165 个数据按每4 个数据为一组分成162 组，其中前137 组（1993 年06 月～2016 年10 月）作为训练数据，后25组（2016 年11 月～2021 年07 月）作为测试数据。每组数据中前3 个为输入样本，最后一个为输出样本。

（2）核函数及参数的确定

核函数的选取决定SVR 回归模型的精度，文中采用径向基核函数，具有较强的回归能力。同时参数的选取对SVR 预测精度也具有较大的影响，设定惩罚参数C′=12.5，不敏感因子ε=1，径向基核函数σ0=0.03。

（3）预测结果

测试集的真实值和预测值对比如图7 所示，测试集误差的方差为10.029，往后预测结果如图8所示。

图7 SVR 测试集预测值和真实值对比图

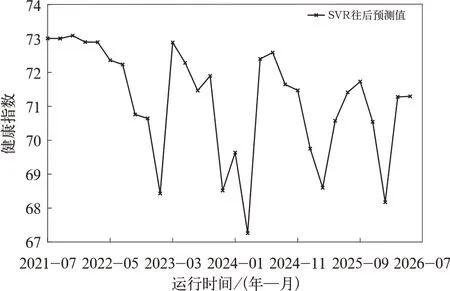
图8 SVR 往后预测结果

3.2.3 组合预测

文中采用协方差优选法确定组合模型中各自的权重，上述SARIMA 和SVR 模型预测误差的方差σ1=9.397，σ2=10.029，代入式（12）中，得SARIMA 预测模型的权重ω1=0.52，SVR 预测模型的权重ω2=0.48。

将上述2 个模型权重代入式（10）中，得组合预测值Y=0.52YSARIMA+0.48YSVR，测试集3 种预测模型的预测值和真实值对比结果如图9 所示。

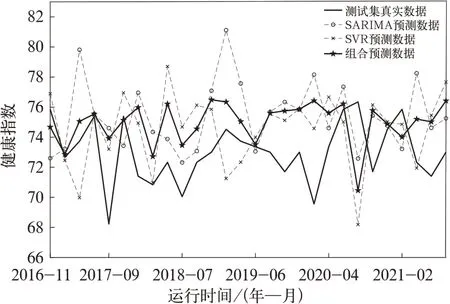
图9 测试集3 种模型预测和真实值对比图

选用均方误差（Mean Square Error，MSE）评价指标对3 种预测模型进行评价，公式为式（13）：

式中：n为测试集的样本数；Ym为测试集真实值；′为测试集预测值。

3 种预测模型的均方误差MSE比较见表3，SARIMA-SVR 组合预测模型相比于单个模型能有效减少误差，提高预测精度。因此采用该组合模型往后进行预测，结果如图10 所示。

表3 3 种预测模型误差分析结果

图10 组合预测模型的预测结果

3.3 转向架系统剩余寿命

由表3 可知，SARIMA 和SVR 组合预测模型的预测效果最好，因此从第3 次架修后将实际的健康指数和组合预测的结果结合，采用K邻近法将杂点用前后两个均值代替，再进行拟合，如图11 所示，拟合度R2=0.887 6，得到转向架健康指数和运行年份的函数关系为式（14）：

图11 健康指数拟合结果

由式（14）转化得运行时间T为式（15）：

由上述可知HIL=70，即将y=70 代入式（15），得该车型转向架系统总寿命T0为33.0 年，该车型从开始运行到2021 年7 月，转向架系统已使用寿命T1为28.1 年，则代入式（4）得该车型转向架系统剩余寿命ΔT约为4.9 年。

4 结论

（1）根据地铁车辆转向架系统历史的故障率，通过转化得到其对应的健康指数，提出SARIMA和SVR 模型结合的组合模型，并采用协方差优选法得到SARIMA 和SVR 模型各自的权重，基于组合模型对其健康指数进行预测，结果表明组合模型的均方误差MSE均低于单个预测模型，提高了预测精度。

（2）根据建立的历史和预测健康指数与运行时间的数学模型，分析其健康状态随运行年限的变化规律，以此得到剩余寿命。以某地铁车辆转向架系统为例进行算例分析，验证了该方法的可行性，为后期维护、维修、退役及延寿决策提供理论数据分析支撑。