基于数据特征的接触网补偿装置卡滞识别方法研究
逯昊舒,张文轩,王 婧,杨志鹏,王 斌,寇鸿博
(1 中国铁道科学研究院 研究生部,北京 100081;2 中国铁道科学研究院集团有限公司 基础设施检测研究所,北京 100081)
中心锚结与下锚补偿装置是接触网的重要组成部分。中心锚结装置用于限制承力索和接触线的异常窜动,并可有效缩小事故范围,便于及时排除故障,恢复运行;下锚补偿装置用于补偿接触线和承力索因温度变化而产生的张力变化,从而使张力保持恒定[1]。中心锚结及下锚补偿装置若存在状态异常或发生卡滞等问题,会导致接触线高度、弓网接触力发生较大变化,影响弓网正常取流,严重时会发生弓网故障,影响列车行车安全。为快速找到此类缺陷,文中提出一种分析故障发生后弓网接触力和接触线高度数据特征,以寻找中心锚结及下锚补偿装置缺陷的方法。
高速铁路弓网综合检测装置(1C)安装于高速综合检测列车上,能同时对接触网几何参数、弓网接触力、接触网电压、接触线硬点、弓网离线燃弧等参数进行测量[2],并生成1C 检测波形文件。文中依据其1C 检测波形文件,进行下一步工作。
1 波形数据特征分析及预处理
1.1 数据特征分析
接触网以锚段为一个自然分界,下锚补偿装置位于锚段两侧,寻找此类缺陷宜以一个锚段为独立单元,分单元独立评价。锚段与锚段之间一般以四跨、五跨过度,称为四跨锚段关节、五跨锚段关节。过度区段存在接触线高度相等的位置,称为等高点。文中采用等高点作为锚段的起始、终止位置,并利用文献[3]中方法识别等高点。
在确定寻找缺陷的特征变量时需考虑以下因素:
(1)特征变量是否为缺陷位置的直接体现。经过对波形的整理归纳和现场复核,较为典型的下锚补偿装置卡滞问题波形如图1 所示,特点表现为在锚段中部接触线高度异常突起,波动剧烈;弓网接触力在对应位置出现异常值,变化迅速。

图1 典型缺陷1C 波形图
(2)特征变量是否关联性较小。接触线高度与弓网接触力关联性较小[4],且分别从接触网几何参数、弓网受流参数描述该问题,具有完备性。故选择接触线高度和弓网接触力作为判断此类缺陷的特征变量。
1.2 数据预处理
接触线高度和弓网接触力在检测过程中由于干扰等原因会产生异常数据,具体表现为持续若干数据点为零或为常数。通过检测数据是否持续为零或为常数,可以找到异常数据所在位置。为避免在下一步中产生误判,需对异常数据进行修正。采用线性插值进行修正在此处可取得较好的效果,且其可执行性高、原理简明,故可采用该方法对异常数据进行修正,操作步骤如下。
设第一个异常数据前一个正常数据点弓网接触力/接触线高度坐标为ym,最后一个异常数据后一个正常数据点弓网接触力/接触线高度坐标yn,则中间的异常数据点由公式(1)得到的数据替代。
替代效果如图2 所示。
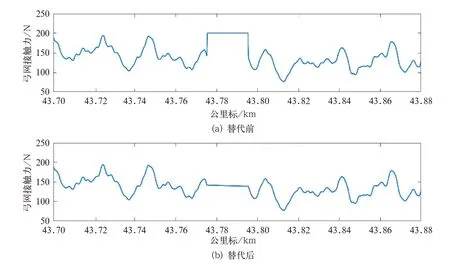
图2 弓网接触力异常数据替代效果图
2 算法提出
由特征变量判断接触网中心锚结及下锚补偿装置缺陷的总体思路:数据预处理→接触线高度异常识别→弓网接触力异常识别→逻辑综合得出异常锚段。
2.1 接触线高度异常识别
接触线高度数据随里程变化,可将其视为一个等效时间序列。采用滑动四分位差距法[5]进行异常检测具有较好的效果。
首先定义窗长W=800,步长为1,计算窗内Q3(上四分位数)、Q2(中位数)、Q1(下四分位数)、IQR(四分位距)。令:
式中:取a0=1.3,x[0]取窗内中点,得到点(x[0],y[0])。将滑动窗右移一个单位,即接纳一个新数据,抛弃一个旧数据,重复上述操作,得到点(x[1],y[1])。将滑动窗从检测波形首端移动到检测波形末端,得到一系列数据点(x[0],y[0])、(x[1],y[1])、…、(x[n],y[n]),利 用3 次样条插值[6]将其用平滑的曲线连接,得到曲线y=f(x),称其为上界线。
上界线为利用窗内数据及窗的滑动形成的警示线,若接触线高度没有向上突变,则不会超过上界线,反之若接触线高度超过上界线,则认为接触线高度存在异常。根据其特点制定2 条规则,需同时满足才判定为缺陷。
(1)接触线高度数据超过上界线连续48 个点以上。接触线高度数据超过上界线需达到一定点数,如图3 所示,以保证接触线高度异常突起显著且持续一段距离。

图3 高度异常识别原理说明图
(2)设接触线高度为hji,i=1,2…,对应位置上界线高度为hi,i=1,2…,i从接触线高度超过上界线第一个点算起,到超过上界线最后一个点为止。定义为式(3):
2.2 弓网接触力异常识别
由于弓网接触力变化迅速,异常值通常出现在跨中,可以一跨为单位,通过锚段中部若干跨内弓网接触力的统计量来进行异常识别。设一跨内弓网接触力标准差为σ、平均值为Fˉ,为实现其自适应性,若满足σ>0.2Fˉ,则认为此跨接触力波动大,定义此锚段为接触力异常疑似锚段。
对于接触力异常疑似锚段,根据波形数据特点及弓网接触力自身特点、铁路线路结构特点,制定3 条规则进一步筛选出确定的接触力异常锚段,所述规则均需满足。
(1)受地形地貌条件限制,有些锚段跨数较少。由于在锚段关节处弓网接触力波动大,属于正常现象,故需避开锚段关节所在跨而计算锚段中间的跨,划分规则按式(4)、式(5)执行。
式中:x为锚段包含跨数;y为需要判断的中间跨数;A为x在不同范围时所取具体跨集合;card为集合的基数。
为了更好理解式(4)、式(5)所述规则,举例说明。若一个锚段有11 跨,则x=11,代入式(4)、式(5),得y=5,A={4 5 6 7 8}。其含义为需计算、判断中间5 跨,分别为4、5、6、7、8 跨。具体位置如图4 所示。

图4 11 跨锚段1C 波形图
(2)锚段中部一跨内弓网接触力标准差σ要满足σ≥a2,a2可按多条线路统计规律取32.34 N。按该规则筛选出接触力变化较大的跨。
(3)σi为第i跨弓网接触力标准差,定义pi为式(6):
需满足pi≥a3,a3可按多条线路统计规律取28%。
该条规则含义为筛选出锚段中间标准差(σ)占比较大的跨,以区别图5(a)、图5(b)这2 种情况。图5(a)为整锚段弓网接触力波动均较大,图5(b)为锚段中部分跨弓网接触力波动大,则通过此规则排除情况如图5(a)所示,留下情况如图5(b)所示。
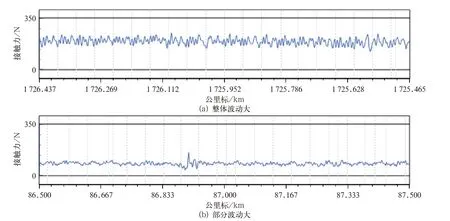
图5 条件3 辅助说明图
2.3 综合得出异常锚段
对某条线路进行接触线高度异常识别,设得到异常锚段为[a,b,c],对该线路进行弓网接触力异常识别,设得到异常锚段为[b,c,d],则判定[b,c]为异常锚段。即对接触线高度异常锚段集合与弓网接触力异常锚段集合取交集。
3 实例验证
3.1 200~250 km/h 线路
某条线路为速度250 km/h 等级线路,对其进行人工查验发现48 号锚段(44.98~46.08 km)、49号锚段(46.08~46.90 km)存在异常,检测波形如图6、图7 所示。

图6 48 号锚段检测波形
利用上述算法对此条线路进行计算,得到接触线高度异常锚段为48、49 号锚段;得到弓网接触力异常锚段为48、49 号锚段,结果见表1。按照规则综合得出异常锚段为48、49 号锚段,验证结果正确。
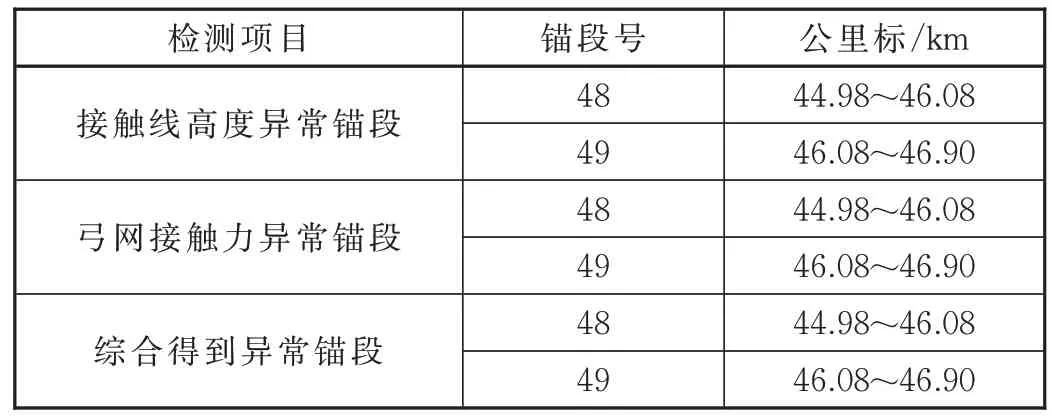
表1 线路1 检测检验结果
3.2 300~350 km/h 线路
某条线路为速度300 km/h 等级线路,对其进行人工查验发现213 号锚段(1 702.31~1 703.23 km)、256 号锚段(1 743.09~1 743.95 km)、259 号锚段(1 745.72~1 746.58 km)存在异常,检测波形如图8~图10 所示。

图8 213 号锚段检测波形

图9 256 号锚段检测波形

图10 259 号锚段检测波形
利用上述算法对此条线路进行计算,得到接触线高度异常锚段为213、256、259 号锚段;得到弓网接触力异常锚段为19、20、213、256、259 号锚段,结果见表2。按照规则综合得出异常锚段为213、256、259 号锚段,验证结果正确。

表2 线路2 检测检验结果
4 结果分析
通过对不同速度等级线路验证,证明了此算法的有效性。考虑到实际情况中各种因素相互影响,该算法在以下方面还有待提高。
(1)可以考虑根据线路速度等级、悬挂类型等因素分类,针对不同线路类型给出不同的系数。
(2)对中心锚结及下锚补偿装置缺陷形成原因进行分类,分析故障原因并统计不同故障类型占比,针对不同原因给出不同的系数。
5 结论
文中提出一种通过1C 检测波形寻找中心锚结及下锚补偿装置缺陷的方法。该方法针对缺陷位置波形主要特征,确定了接触线高度与弓网接触力两个特征变量。对接触线高度采用滑动窗进行识别,对弓网接触力采用按跨计算标准差进行识别,并设定相应规则,最终寻找出缺陷发生位置。经过验证,该方法可以正确识别出缺陷位置,可用来指导维修人员快速定位缺陷位置,为此类问题快速查找和及时整治提供数据支持。

