钢柱-钢板剪力墙耦合结构性能化抗震设计及评估

赵家正,张 博,伍云天,2

(1. 重庆大学 土木工程学院,重庆 400045; 2. 重庆大学 山地城镇建设与新技术教育部重点实验室,重庆 400045)

0 引言

钢板剪力墙结构体系凭借其塑性性能优越、滞回特性稳定的优点,十分适用于高烈度地震区的建筑[1-2]。其设计参数对其抗震性能的影响也已经通过数值或试验方法进行了大量研究[3-6],已经成为工程中可靠的抗震体系之一。与钢筋混凝土剪力墙结构相比,钢板剪力墙自重更轻,所以其传递给基础的竖向荷载较小,因此可以在保证结构良好延性的前提下降低基础的造价,而且钢板剪力墙的墙体厚度更小,能够节约建筑空间。但是钢板剪力墙主要通过墙肢底部抵抗地震作用,抗震设防机制较为单一,在地震作用下损伤集中在墙肢底部,震后不易修复[7]。为了减少剪力墙结构的损伤,并扩展剪力墙结构体系的适用范围,推动剪力墙朝向可恢复功能防震结构的方向发展,本文利用钢连梁连接钢板剪力墙和两侧钢柱形成新型钢柱-钢板剪力墙耦合结构(steel column-steel plate shear wall coupled structure,SC-SPSW)体系,该体系通过钢连梁将钢板剪力墙与两侧的钢柱连接起来。其中钢连梁和边柱之间采用铰接,以确保只传递剪力,而钢连梁与钢板剪力墙之间为刚接,保证同时传递剪力和弯矩。因此,SC-SPSW结构可以通过钢连梁耗能来减少结构损坏,并实现双重抗震机制。传统的设计方法是基于结构的弹性响应,往往需要多次迭代,导致设计过程复杂并忽视结构的塑性响应。因此,需要在现有研究基础上开发针对SC-SPSW结构体系的设计方法,实现剪力墙结构体系设计方法的有益补充。

本文采用基于能量平衡的塑性设计理念,并结合相关规范[8-11]推导出SC-SPSW体系的设计方法。利用SAP2000软件建立了12个SC-SPSW体系算例并对其进行了拟静力分析和非线性动力时程分析,研究结构的屈服机制以及耦连比对结构受力性能的影响。研究表明,应用该设计方法的结构算例能够实现双重抗震机制,并满足预期的性能目标。

1 性能化塑性设计方法

1.1 性能目标

SC-SPSW体系通过钢连梁将钢板剪力墙与两侧的钢柱连接起来形成耦合结构体系,如图1(a)所示;其理想屈服机制需要体现出钢连梁-钢板剪力墙双重抗震防线的优势,如图1(b)所示。在中震作用下,部分内嵌钢板屈服,接近一半钢连梁(steel coupling beam, SCB)剪切屈服消耗大部分地震输入能。结构出现损伤但修复后可以继续使用,结构整体保持弹性。在大震作用下,大部分钢连梁屈服并充分耗散能量、边缘框架梁(horizontal boundary element, HBE)弯曲屈服、边缘框架柱(vertical boundary element,VBE)的柱脚出现塑性铰,结构整体处在塑性阶段但不会发生倒塌。

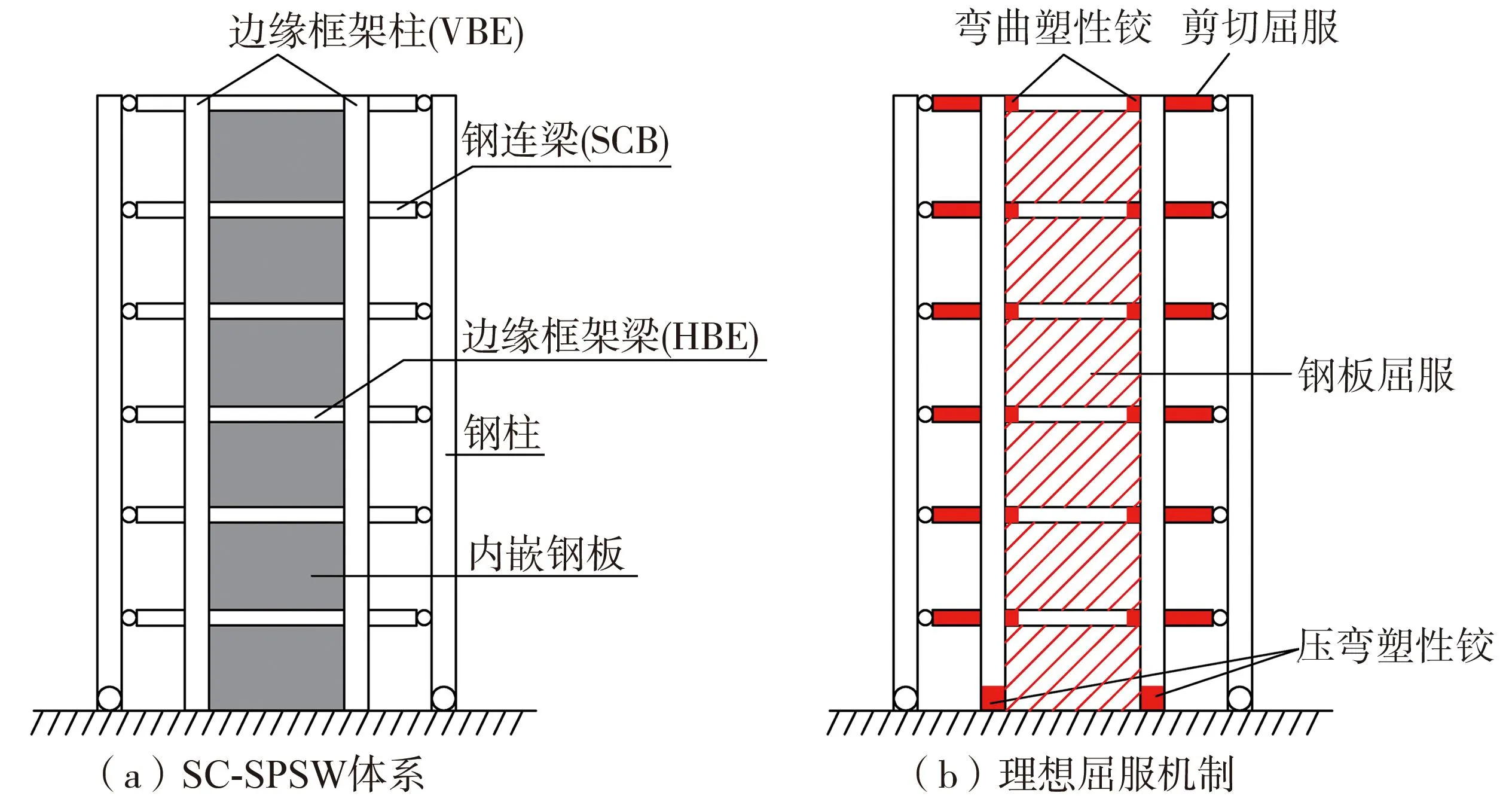
图1 SC-SPSW体系理想屈服机制Fig.1 Ideal yield mechanism of SC-SPSW system

同时结合规范中对剪力墙的层间位移角限值[8-9],SC-SPSW体系的性能目标为:在中震作用下,一半钢连梁率先屈服消耗大部分地震能,结构发生中等程度的损伤但修复后可以继续使用,此时结构层间位移角不大于1/200;大震作用下,大部分钢连梁屈服并充分耗散能量、VBE构件柱脚可以出现塑性铰,结构损伤严重但不会倒塌,此时结构层间位移角不大于1/50。

1.2 能量平衡原理

地震输入能E1的一部分以动能和弹性应变能Ee储存在结构体系中,剩余部分会被结构自身的阻尼和塑性应变能Ep消耗。基于以上原理,GOEL等[12]提出了适用于工程的简化能量平衡方程,表达式为

η(Ee+Ep)=γE1

(1)

(2)

式中:γ为地震输入能修正系数;η为滞回耗能修正系数,参考钢板剪力墙体系的研究[13],本文取η=0.75;μ为目标延性系数;Rμ为延性折减系数。在计算弹性应变能和塑性应变能时将结构体系视为理想弹塑性体系,能量平衡示意图如图2所示。将实际多自由度体系的最大地震输入能近似等效为多个弹性单自由度体系最大地震输入能之和。

图2 能量平衡示意图Fig.2 Illustration of energy balance

所以地震输入能计算[14],得

(3)

结构的弹性应变能应根据屈服力及屈服位移计算[15],得

(4)

式中:M为结构质量;G为结构重量;g为重力加速度;T为自振周期。

结构的塑性应变能计算,得

Ep=∑Fihiθp=Vyθp∑λihi

(5)

式中:Fi为结构第i层的侧向力;hi为结构第i层的离地高度;θp为目标塑性位移角,其与目标位移角θy和屈服位移角θu相关,θp=θu-θy;Vy为结构基底剪力;λi为侧向力分布系数。

传统侧向力分布模式只考虑了结构在弹性阶段的特性,对结构进入塑性阶段后的地震响应无法较好地预测。本文采用了CHAO等[16]提出的基于结构塑性阶段层剪力分布的侧向力分布模式,表达式为

(6)

(7)

(8)

结构总倾覆力矩MOTM为

(9)

1.3 CR设计

由于SC-SPSW体系的传力机制和联肢剪力墙类似[17],因此本文也将耦连比(coupling ratio, CR)作为SC-SPSW体系的主要设计参数。SC-SPSW体系的CR定义为两侧钢边柱通过钢连梁耦合作用形成的拉-压力偶MC与结构的总倾覆力矩MOTM的比值。CR计算如下:

(10)

GORJI AZANDARIANI等[18]在考虑了结构性能参数、结构屈服机理等因素后,提出SC-SPSW体系合理的CR范围是0.3～0.5。但其研究模型高度较低,与本文研究结构的高度相差较大。因此为了更全面的研究CR对结构的影响,本文设计CR范围是0.3～0.6。

1.4 钢连梁与钢柱设计

SC-SPSW体系中钢连梁与钢柱之间的连接方式设置为铰接,钢柱只承受钢连梁传递来的竖向力,两边钢柱的拉压轴力大小相同。钢连梁的总剪力需求为

(11)

(12)

式中:ψi为钢连梁剪力分配系数。文献[20]建议将钢连梁设计为剪切屈服,因为相比于以弯曲塑性变形为主的钢连梁,以剪切塑性变形为主的钢连梁的耗能能力更强。本文参照美国规范[10]将钢连梁参数按照剪切屈服取值,表达式为

lb<1.6MP/Vp

(13)

(14)

式中rov为加强系数。

1.5 钢板与边缘框架设计

由于边缘框架的设计还未完成,因此需要先估算内嵌钢板的厚度。在估算钢板厚度时,为了减少一些不必要的迭代计算,可以假设SC-SPSW体系中钢板剪力墙结构的承载力全部由其钢板承受。同时可令每一层内嵌钢板的拉力场倾角αi恒等于45°,侧向力由内嵌钢板的水平力分量抵抗。则钢板厚度可用式(15)估算:

(15)

本文主要参照美国规范[10]对边缘框架进行计算。假设内嵌钢板全截面屈服完全形成拉力场,HBE构件的理想屈服机制是在梁两端出现塑性铰[21],最大弯矩处至梁左端的长度xs,i应满足式(16):

(16)

式中:MHBE,i第i层HBE传递给VBE的弯矩值;为ωv,HBEi为第i层HBE受到内嵌钢板作用力的竖直分量。VBE构件的理想屈服机制是在底端出现压弯塑性铰。所以最大弯矩出现处的高度hs应满足式(17):

(17)

式中:MVBE为VBE承受的力偶;ωh,VBE1为VBE收到内嵌钢板作用力的水平分量;H1为结构底层层高。HBE和VBE截面设计需要满足规范[10-11]中强度及刚度验算。同时为了保证钢板完全屈服耗能和VBE在钢板张力场发展出其全部能力之前不会屈服,在确定边缘框架尺寸后需根据实际承载力进行钢板厚度迭代计算。

1.6 设计算例

本文按照上述设计方法设计了不同CR(0.3,0.4,0.5,0.6)、不同层数(10层、15层、20层)一共12个SC-SPSW体系算例。算例按照“W-N-CR”方法编号,其中“W”表示SC-SPSW体系,“N”代表结构总层数,“CR”代表设计耦连比,比如耦连比为0.3,总层数为10的SC-SPSW体系表示为W-10-0.3。原型结构平面布置图和SC-SPSW结构立面图,楼板厚度取100 mm,如图3和图4所示。型钢构件截面尺寸如图5所示。结构基本设计信息如表1所示。因篇幅所限,本文只列出W-10-0.3算例的结构设计参数,如表2、表3所示,其余算例不再具体列出。

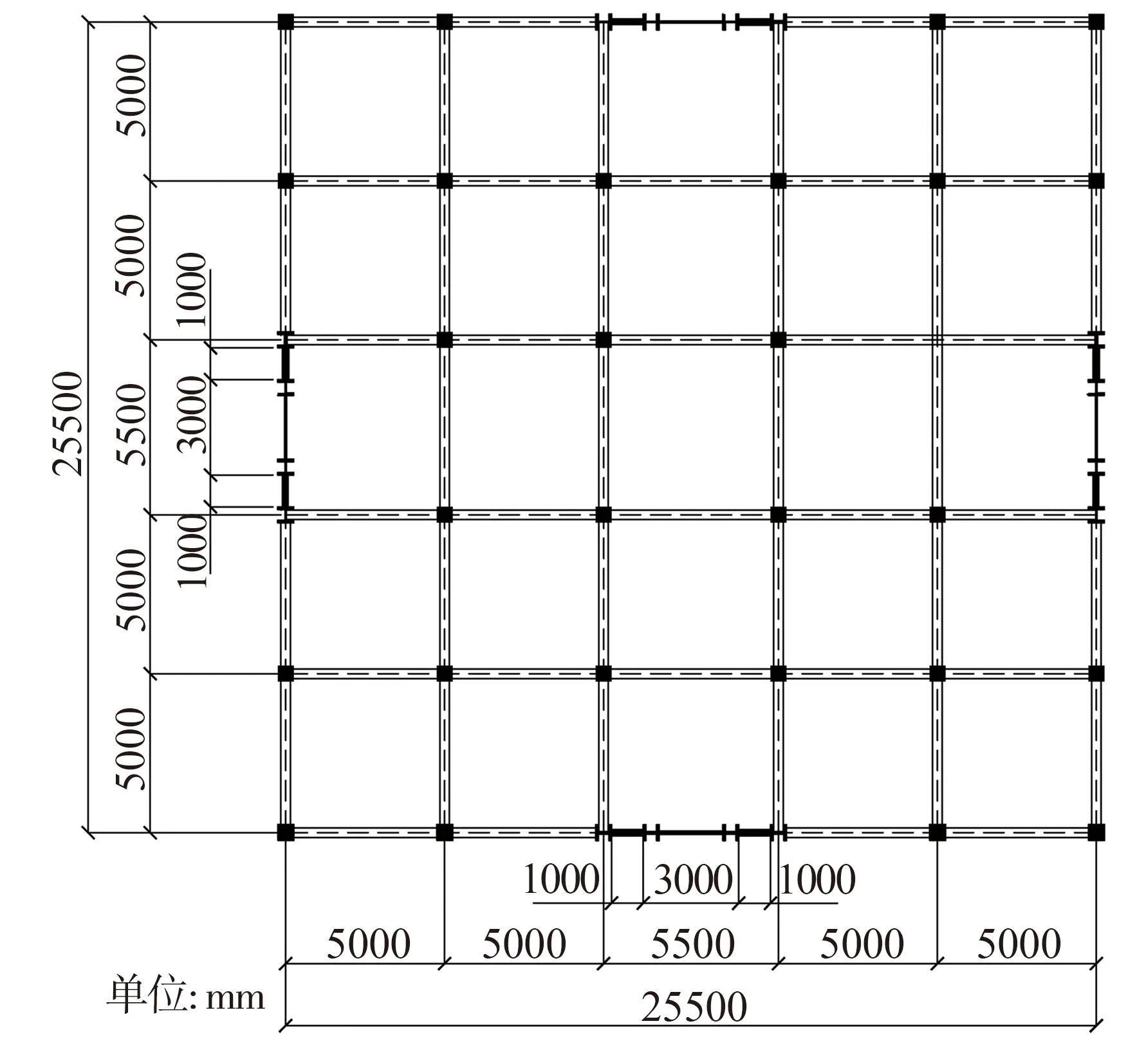
图3 原型结构平面布置图Fig.3 Layout plan of prototype structures

图5 型钢构件截面尺寸图Fig.5 Cross-section of steel components

表1 结构基本设计信息Table 1 Basic structural design information设计类别类别参数信息设计总信息重要性类别丙类层高/m3.6设防烈度区8度0.2 g区设计地震分组第三组场地类别Ⅱ类阻尼比0.05抗震等级二级材料信息型钢Q355钢板Q235楼面及屋面荷载标准值/(kN/m2)楼面恒荷载3.05楼面活荷载2.50屋面恒荷载4.77屋面活荷载2.35

表2 W-10-0.3型钢构件尺寸Table 2 Sectional dimension of steel members of W-10-0.3结构编号构件h×b×t1×t2/mmW-10-0.3钢边柱200×100×4.5×7VBE构件400×300×10×16一至三层钢连梁110×74×5×9四至七层钢连梁105×70×5×9八至十层钢连梁100×68×5×8一至三层HBE构件200×150×7×10四至七层HBE构件180×150×7×10八至十层HBE构件150×150×7×10表3 W-10-0.3钢板厚度Table 3 Steel plate thickness of W-10-0.3结构编号层数钢板厚度/mmW-10-0.3一至三层2.8四至七层2.2八至十层1.5

2 有限元建模及对比

2.1 数值建模

本文采用SAP2000软件进行等比例模型建立。利用非线性分层壳单元来建立剪力墙等效模型,厚度和模型钢板厚度相同,利用框架单元模拟钢连梁、边缘框架及钢边柱。钢连梁和钢边柱之间是铰接,其他构件之间均为刚接。根据SC-SPSW的理想屈服机制,在HBE定义M3弯矩铰,在SCB定义V3剪切铰,在VBE柱脚定义P-M2-M3铰。

钢材本构关系选用考虑一定程度包辛格效应的双折线随动强化模型,服从Mises屈服准则。Q235屈服强度取235 MPa,极限强度取370 MPa,Q355屈服强度取355 MPa,极限强度取450 MPa。钢材弹性模量均为200 GPa,泊松比取0.3。内嵌钢板由于加工和运输过程中的损耗会产生初始几何缺陷。初始几何缺陷将会对钢板的变形和受力产生不利影响,因此选取钢板最容易发生的变形的屈曲模态,然后将该模态下变形施加在内嵌钢板上作为初始缺陷。初始缺陷的幅值通常取为内嵌钢板长边的1/1000～1.5/1000。

2.2 试验对比分析

目前国内外并没有SC-SPSW体系的试验研究,由于SC-SPSW体系和联肢钢板剪力墙具有类似的抗震防线[18],所以本文选择了联肢钢板剪力墙结构试验进行对比验证。为了验证上述建模方法的有效性,本文选取了一个缩尺比例为0.4的3层联肢钢板剪力墙构件[22]进行模拟对比分析。该试验采用位移控制加载,分别取顶层位移角为0.1%、0.25%、0.5%、1%、1.5%、2.0%、2.5%、3.0%和4.0%逐级往复加载,每个级别循环2次,最后在顶层位移角为-2.0%时停止加载。模拟取试验实测的平均值作为材料的性能指标。

模拟滞回曲线与试验滞回曲线对比如图6所示。由图可知,模拟分析的滞回曲线的整体形状和试验值基本贴合,且每一个滞回圈的峰值承载力也几乎和试验值相同。同时模拟分析的正向峰值承载力比反向峰值承载力略低,这与试验结果也是一致的。综上所述,在考虑实际试验与模拟之间有一定差异(底层钢板的约束条件难以模拟)、材料及构件存在瑕疵无法利用初始缺陷完全拟合的情况下,可以认为建模方法是准确有效的。

图6 滞回曲线结果对比Fig.6 Results comparison of hysteretic curves

3 Push-over分析

常用的侧向力模式有均匀分布型、倒三角分布型和模态分布型,这3种侧力模式在结构弹性阶段的精度较好。但是结构在进入塑性阶段后,其塑性发展对侧向力分布模式有不可忽略的影响。因此本文选择考虑了结构塑性发展的侧向力加载模式。

3.1 推覆曲线

从拟静力分析中获取的12个算例的推覆曲线,如图7所示,图中的“△”点为结构一半钢连梁屈服的状态,“□”点为VBE构件的柱脚处达到屈服应力时对应的状态。随着CR的增加,不同层数的结构都表现出初始弹性刚度略微增加的现象。当最大层间位移角相同时,CR越大,结构的基底剪力就越大,这说明增加CR可以明显提高结构在地震作用下的峰值承载力。曲线中对应一半钢连梁屈服时的数据点均位于曲线的拐点处,且均在VBE构件屈服之前,说明SC-SPSW体系将一半钢连梁屈服作为第一道抗震防线是合理的,并可作为结构体系进入非弹性状态的判断依据。随着CR的增大,曲线中“△”点与“□”点之间的距离越来越短,这意味着在一半钢连梁屈服后,结构在发生严重损坏之前的变形能力越来越差。因为较大的CR使钢连梁的剪力更大,从而钢连梁传递给VBE构件的竖向力也更大,过大的轴力会使VBE构件的更早的屈服,所以CR的值不应该过大。

3.2 整体屈服机制

为研究SC-SPSW体系的整体屈服机制,图8统计了12个算例在推覆分析中“一半钢连梁屈服”和“VBE构件柱脚屈服”时的最大层间位移角。钢连梁屈服时最大层间位移角分布在0.0038～0.0050区段,而中震下结构的最大层间位移角不能超过1/200,这意味着结构在其最大层间位移角超过中震下的限值之前,会有一半钢连梁屈服,这与SC-SPSW体系的性能目标相符,结构的第一道抗震防线可以得到满足。VBE构件柱脚屈服时,除了W-10-0.6和W-15-0.6之外,所有结构的最大层间位移角均大于大震下结构的最大层间位移角1/50,这意味着结构在其最大层间位移角超过大震下的限值之前,VBE构件可能还没有屈服,所以结构不会倒塌,这与性能目标相符,结构的第二道抗震防线也可以得到满足。而W-10-0.6和W-15-0.6是因为CR较大,钢连梁传递给VBE构件的竖向力较大,所以VBE构件更容易屈服。由图8可知,随着CR的增大,钢连梁屈服时的最大层间位移角逐渐增大,而VBE构件屈服时的最大层间位移角逐渐减小。这说明对于SC-SPSW体系,为了实现钢连梁率先屈服耗能而后VBE构件屈服,不应该选用过大的CR。

图8 不同性能状态的结构最大层间位移角Fig.8 The maximum inter-story drift ratio under different structural performance states

4 非线性动力时程分析

4.1 地震波选取

本文利用文献[23]提出的双频段选波法选择了5条天然地震波数据,并生成2条人工地震波数据,7条地震波信息如表4所示。所选取的7条地震波反应谱如图9所示。平均反应谱与设计反应谱对比如图10所示。由图可知,平均反应谱与设计反应谱吻合较好。

表4 地震波记录Table 4 Ground motion records

图9 地震波反应谱Fig.9 Response spectrum of ground motions

图10 平均反应谱曲线对比Fig.10 Comparison of average response spectrum curves

根据GB 50011—2010《建筑抗震设计规范》[8]的要求,用于动力时程分析所用地震波的运动峰值加速度(PGA)需要进行调幅以满足设计分析要求,调幅方法为

(18)

4.2 最大层间位移角

12个模型在中震作用下的最大层间位移角平均值如图11所示,图中虚线对应的就是中震作用下体系的极限状态。由图可知,12个模型的最大层间位移角平均值均小于0.005,符合中震作用下的性能目标。12个模型在大震作用下的最大层间位移角平均值如图12所示。除了W-20-0.3外所有算例的层间位移角均未超过0.01,而W-20-0.3的层间位移角没有超过0.012。而大震下的性能目标为不超过层间位移角限值0.02,所以12个模型满足大震下的性能目标。

图11 中震最大层间位移角平均值包络Fig.11 Mean value envelopes of the maximum inter-story drift ratio under moderate earthquakes

图12 大震最大层间位移角平均值包络Fig.12 Mean value envelopes of the maximum inter-story drift ratio under rare earthquakes

中震和大震下的曲线整体走势均较为平滑无明显变形突变特征,说明结构整体刚度分布均匀,没有薄弱层出现。在层数相同时,CR从0.3增大到0.6,除底层之外的最大层间位移角平均值都明显减小。这说明CR较大时,钢连梁对结构整体能够产生较强的约束作用,进而增大结构的刚度,降低结构的变形能力。由图12可知,在大震作用下,CR从0.3增加到0.4引起的层间位移角的减小要比CR从0.5提高到0.6明显,这意味着CR的值越大,提高CR所带来的结构刚度提升效果越小。

4.3 层间剪力分布规律

各模型顶层层间剪力最大值为基准对每层层剪力进行归一化处理,给出了12个模型在中震下最大层剪力分布系数如图13所示。各结构的层剪力分布变化比较规律,不存在明显的内力突变,说明结构没有薄弱层。由图可知,本文采用的分布模式稍微低估了顶部和底部层剪力分布,高估了中间层的层剪力分布。由于设计层剪力分布系数高估了中间层的层剪力,所以底层墙肢的设计倾覆力矩会更大。而SC-SPSW体系的墙肢部分是弯曲破坏控制的,所以该设计侧向力分布模式一定程度上使结构更加安全。

图13 层剪力分布规律Fig.13 Distribution of inter-story shear

4.4 钢连梁屈服率

实现SC-SPSW体系理想的屈服机制的关键是在中震作用下接近一半的钢连梁可以率先屈服耗能。图14给出了中震下钢连梁的平均屈服率。钢连梁屈服率为结构中已屈服的钢连梁数与结构中钢连梁总数的比值。由图14可知,钢连梁屈服率均大于或等于50%,符合理想屈服机制的要求。而且可以从图中发现,CR越大,钢连梁的屈服率越小。

图14 钢连梁屈服率Fig.14 Yield ratio of steel coupling beams

5 结论

本文采用基于能量平衡的塑性设计理念设计了12个SC-SPSW算例,并通过SAP2000进行Push-over分析和非线性动力时程分析,研究其屈服机制以及耦连比对结构受力性能的影响,主要得到如下结论:

1)采用本文基于性能化的塑性设计,在拟静力分析和非线性动力时程分析验证了其能够实现理想的双重抗震防线机制,并使结构达到预期性能目标。在本文的算例中,当CR取值为0.3、0.4、0.5时分析结果较好,CR过大会对结构有不利影响。

2)从拟静力分析结果中发现,随着CR的增大,一半钢连梁屈服时结构的最大层间位移角逐渐增大,而VBE构件屈服时的最大层间位移角则逐渐减小,这说明CR过大可能会影响钢连梁率先屈服耗能而后VBE构件屈服。

3)从非线性动力时程分析结果中发现,CR的值越大,继续提高CR所带来的结构刚度提升效果越小,并且钢连梁在中震下的屈服率会降低。

4)本文采用的侧向力分布模式会使底层墙肢的设计倾覆力矩会更大。而SC-SPSW体系的墙肢部分是弯曲破坏控制的,所以该设计侧向力分布模式一定程度上使结构更加安全。