考虑套筒灌浆随机缺陷的装配式剪力墙结构可靠度评估

薛 亮,孙千伟,任晓丹,秦夏强,许海岩

(1. 同济大学 土木工程学院,上海 200092; 2. 中国二十冶集团有限公司,上海 201999)

0 引言

近些年来,装配式结构在各地得到推广,而套筒灌浆连接作为竖向预制构件中受力钢筋的主要连接方式,其质量安全与力学性能对结构整体抗震性能的影响成为了工程领域中关注的话题[1]。在建造过程中,预留孔洞偏差较大、施工工艺不成熟等因素,造成了套筒灌浆质量缺陷问题时有发生。目前,有大量学者研究了套筒灌浆缺陷对装配式结构抗震性能的影响。匡志平等[2]、李向民等[3]对具有灌浆缺陷的钢筋套筒连接接头进行了单调拉伸和反复拉压试验,结果表明,灌浆缺陷将降低试件的承载能力与变形能力。李全旺等[4]对不同程度的均匀缺陷、轴向缺陷、环向缺陷和斜向缺陷的套筒连接接头进行了单拔试验,结果表明,在灌浆密实的套筒中,钢筋达到极限应力后发生拉断破坏;存在灌浆缺陷时,套筒的连接性能有所下降,可能发生界面粘结破坏;当灌浆缺陷程度较高时,钢筋在屈服之前套筒灌浆连接就己失效,且灌浆缺陷越大,承载能力越低,钢筋的力学性能越不能充分发挥。刘香等[5]、钱稼茹等[6]发现套筒灌浆不密实将导致装配式墙体中的钢筋出现滑移,墙体的滞回曲线捏拢严重,承载能力显著降低。郑清林等[7]、李向民等[8]研究了不同灌浆缺陷类型的预制混凝土柱,发现无灌浆缺陷的预制柱抗震性能与现浇混凝土柱基本相当,存在灌浆缺陷的预制柱其承载力与延性有较为明显的降低。肖顺等[9]、王伟等[10]、吴宣泽[11]对灌浆缺陷的预制混凝土剪力墙进行了抗震性能研究,发现套筒灌浆缺陷将降低剪力墙的耗能能力、承载力、延性和刚度等。李威威等[12]研究了装配式混凝土框架的抗震性能,发现在灌浆缺陷下装配式混凝土框架节点不再符合“强柱弱梁”的设计原则,而是在坐浆层发生剪切破坏,还定量分析了灌浆缺陷程度对框架结构承载能力的影响。

已有学者的研究表明,灌浆缺陷的存在将导致结构的承载能力减低,耗能能力劣化,结构延性变差,甚至破坏模式发生改变。这就不得不在装配式高层剪力墙结构中考虑灌浆缺陷对结构抗震性能造成的影响,由于实验条件及经济成本的限制,有限元模拟成为了分析高层结构抗震性能的有效途径之一。在有限元分析中,如何考虑灌浆缺陷对结构抗震性能的影响是模拟的关键难点。已有的研究[2-12]发现,不管何种灌浆缺陷,都会削弱试件的承载能力。特别在单拔试验研究[4]中,试验结果明确表明,在有灌浆缺陷的试件中,连接接头的承载能力与变形能力均有降低,在缺陷较为严重的套筒接头中,其钢材应力远低于屈服强度构件就已失效,因此,连接接头的承载与变形能力成为有限元分析中考虑灌浆缺陷程度对抗震性能影响的重要因素。

目前,已有较多学者通过考虑灌浆缺陷对连接接头的影响来分析灌浆缺陷下装配式构件的抗震性能。王伟[10]采用纤维梁单元模拟装配式剪力墙,对套筒处钢筋的弹性模量进行折减来考虑套筒的缺陷作用;吴宜泽[11]用弹簧单元模拟钢筋与混凝土之间的相互作用,通过降低弹簧单元的刚度来考虑灌浆缺陷造成的钢筋滑移。李全旺等[4]在梁柱节点中,通过降低节点的转动弹簧刚度来反映连接缺陷对节点受力性能的影响;其在装配式剪力墙体中,通过调整套筒连接部分的应力-应变关系,来模拟套筒缺陷对于剪力墙抗震性能的影响。许铭[13]建立了全装配式剪力墙结构整体有限元模型,通过对刚度与强度的折减来考虑灌浆连接缺陷对装配式结构整体性能的削弱作用。由于装配式施工工艺、建筑材性的变异性等诸多因素,钢筋套筒连接的灌浆缺陷具有一定的随机性。已有的研究在构件层次上分析了灌浆缺陷对结构抗震性能的影响,但依旧缺乏灌浆缺陷以及缺陷随机性对装配式结构整体抗震性能影响的研究。

为了研究灌浆缺陷随机性对结构抗震性能的影响,本文基于某实际工程结构,在非线性有限元分析软件ABAQUS中建立了装配整体式有限元模型。装配式有限元模型在层间竖向连接处用套筒灌浆连接接头进行竖向连接,并通过Python语言对inp文件进行批量处理,对连接接头赋予随机缺陷的力学性能,来等效考虑灌浆缺陷的影响。为了表征钢筋混凝土结构在地震作用下的非线性行为,混凝土采用了双标量损伤本构。为了分析动力作用下钢筋混凝土结构非线性和随机性的耦合效应,将有限元分析结果结合概率密度演化理论,进行了随机非线性反应分析。最后通过设置不同的失效准则,给出了结构在不同的失效阈值下的可靠性概率度量[14-16]。

1 结构分析模型

1.1 有限元建模

本文根据某实际工程中装配式剪力墙结构建立有限元模型,该结构共27层,其中一至四层为现浇剪力墙,五至二十七层为装配式剪力墙。地上建筑面积为17903.46 m2,主屋面高度为78.6 m。其各楼层信息如表1所示。

表1 结构设计基本信息Table 1 Basic information of structural design

本文模型中的主体结构设计使用年限为50 a,工程抗震设防类别为丙类,抗震设防烈度为8度,设计基本地震加速度为0.20g,设计地震分组为第二组,建筑场地类别为三类,特征周期T为0.55 s。所以结构基底输入双向地震波,采用Chi-Chi地震波,如图1所示,主次方向地震动加速度峰值比取1∶0.85。按抗震设防烈度8度要求,将主方向地震动加速度峰值调幅至0.2g,地震动加速度记录时间间隔取0.02 s,地震作用时长取36 s,其加速度反应谱与设计反应谱如图2所示。

图1 X和Y方向地震波 Fig.1 Seismic waves of X and Y direction 图2 加速度反应谱 Fig.2 Acceleration spectrum

本文装配整体式剪力墙结构有限元模型在非线性有限元分析软件ABAQUS中建立,如图3所示,墙体与板采用了分层壳单元,梁柱采用了纤维梁单元,墙体内的分布筋内嵌在壳单元中与混凝土协同变形。墙体中的竖向钢筋是用truss单元建立的,通过共节点的形式与混凝土壳体单元进行连接。为了体现装配式结构套筒灌浆竖向连接的特点,装配式结构中的竖向钢筋在层间连接处用套筒灌浆连接接头进行连接,如图4所示,图中红色表示接头连接位置。其套筒灌浆连接接头可以用beam单元或者truss单元进行建立,本文使用了truss单元,同样使用共节点的方法与墙体共同工作,其连接接头的力学模型使用了1.2节中建立的接头连接模型。混凝土材料采用了双标量弹塑性损伤本构模型[17],水平分布筋采用了理想弹塑性模型,竖向受力钢筋采用了双线性随动强化模型。

图3 装配整体式剪力墙结构有限元模型 Fig.3 Finite element model of assembled integral shear wall structure 图4 钢筋套筒灌浆连接接头Fig.4 Reinforcement grouting sleeve connection joint

1.2 等效套筒灌浆缺陷连接承载力模型

由于套筒灌浆连接在有灌浆缺陷时,连接承载能力有所下降。根据李全旺等[4]的拉拔试验,为反映不同轴向缺陷程度下连接承载能力的变化,本文建立了三段式的不同灌浆缺陷程度的套筒灌浆连接承载力表达式为

(1)

式中:P为套筒灌浆连接接头承载力,当P降低为0时,则彻底失去承载能力;u为滑移量;K1,K2,K3分别为连接接头的等效初始刚度、等效屈服刚度和等效破坏刚度;u1、u2为连接接头的弹性滑移变形、屈服滑移变形。其套筒灌浆连接接头粘结力示意如图5所示。

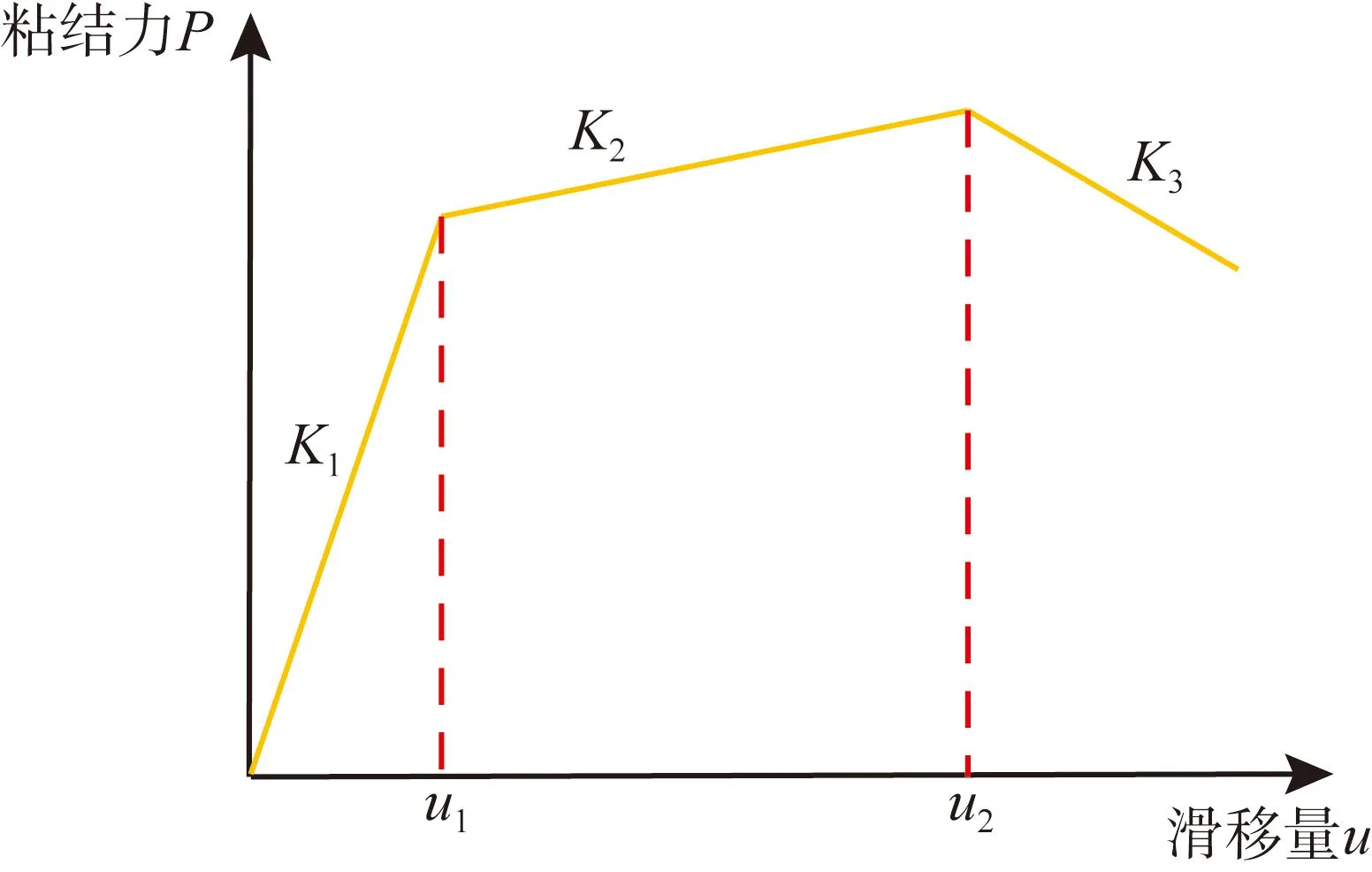
图5 套筒灌浆连接接头粘结力示意图Fig.5 Diagram of bonding force of grouting sleeve connection fitting

考虑到不同灌浆缺陷程度对承载力和破坏模式的影响,建立变量K1,K2,K3,u1,u2在不同灌浆缺陷程度与无灌浆缺陷时的关系式为

(2)

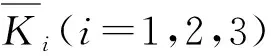
根据李全旺等[4]不同百分比的轴向灌浆缺陷试验,本文拟合出不同百分比轴向灌浆缺陷的αi,βj,如表2所示。

表2 钢筋套筒连接性能拟合参数Table 2 Parameters of steel sleeve connection performance

(3)

式中:d为钢筋直径;L为锚固长度。将拟合的不同灌浆缺陷程度的套筒灌浆承载力与试验粘结滑移曲线对比如图6所示,基本符合不同程度灌浆缺陷对连接接头承载力和变形能力的影响。

图6 不同程度灌浆缺陷下的连接性能拟合公式与试验结果的比较Fig.6 Comparison of the fitted formula for connection performance under different levels of grouting defects with the expermental results

考虑到实际工程中,灌浆缺陷具有随机的特性,则连接接头的承载力也具有随机性,若将连接接头的力学参数服从拉拔试验拟合而成的概率分布,即可考虑灌浆缺陷的随机性影响。由于目前试验数据较少,难以给出较为准确的概率分布模型,参考李全旺等[4]中对灌浆缺陷概率分布的做法,在本文中假定灌浆缺陷在无缺陷和50%缺陷之间随机分布,参数α1、α2、α3、β1、β2在不同缺陷程度之间线性插值,来等效考虑灌浆缺陷随机性对连接接头承载力P的影响。在进行随机非线性分析之前,计算了结构的前6阶振型和自振周期如图7所示。

图7 结构前6阶振型和自振周期Fig.7 The first six orders of vibration and natural period of the structure

1.3 套筒灌浆随机缺陷有限元建模流程

在本文有限元模型中,由于钢筋套筒灌浆连接接头的数量较多,所以借助了Python强大的批量处理功能,对分析文件inp进行了二次开发,实现了套筒灌浆质量缺陷的随机性建模,其建模具体思路如下:

1)对钢筋套筒灌浆连接接头的力学性能进行随机参数选取。由于套筒灌浆质量存在随机缺陷,钢筋套筒连接接头的连接性能将服从一定的概率分布。由于目前试验数据的缺乏,因此在本文中采用1.2节中建立的连接接头的力学性能,连接接头的力学性能在无缺陷和50%缺陷之间随机分布,当试验结果较为充足时,可以直接服从试验结果拟合出来的概率分布。

2)生成与连接接头数量一致的代表点序列,每一个代表点处将按照式(1)赋予一个缺陷程度随机的钢筋套筒连接接头的承载能力属性。此步骤完成了套筒灌浆缺陷自身的随机性,即某些接头连接性能正常;某些接头连接性能略有缺陷;某些套筒灌浆缺陷较大,其接头的力学连接性能削弱较为严重。

3)根据代表点序列中代表点的先后顺序,将其一一映射到有限元模型中的钢筋套筒连接接头单元位置中,此步骤完成了套筒缺陷在空间位置上的随机性即某一接头处的力学连接性能是由代表点序列映射生成。

4)将连接接头位置与连接接头单元编号相对应。在inp文件中,每一单元编号将对应有限元分析模型中的一个单元及位置。

5)将连接接头单元编号所对应的连接接头单元节点编号一一对应。至此形成了连接接头的连接性能、接头位置、接头单元及单元节点编号的闭合分析文件。

1.4 混凝土损伤本构模型

随着建造技术的发展,建筑高度迅速增长,复杂程度也日益增加,从计算分析方法来看,完全采用弹性理论进行分析已很难满足如今的结构分析需求,特别是在地震作用下,结构往往处于多维复杂受力的状态,材性进入塑性或损伤状态,为了精确地模拟装配整体式剪力墙结构在地震作用下的非线性力学行为,混凝土必须采用能够适应复杂应力的损伤本构模型。在本文中混凝土采用了双标量损伤本构模型,该本构模型将有效应力空间正负分解并引入弹塑性Helmholtz自由能势ψ,基于局部能量守恒方程与Clausius-Duhem不等式推导得到受拉和受压损伤演化准则[17],下面将简单介绍该损伤本构模型。

考虑到混凝土材料受拉与受压力学性能的差异,在有效应力空间内将应力进行正负分解,得

(4)

(5)

P-=I-P+

(6)

式中: H(·)为Heaviside函数;n(a)为有效应力张量σ的特征值σa所对应的特征向量;⊗为张量并积符。

混凝土的损伤演化准则可基于不可逆热力学体系,由局部能量守恒方程与Clausius-Duhem不等式推得

(7)

由式(7)可以得到应力-应变关系及损伤耗散不等式为

(8)

(9)

式中Y±和Y-为受拉和受压损伤能释放率。

根据LI等[18]提出的能量等效应变,利用求得的受拉与受压损伤能释放率Y±,可以计算得到能量等效受拉与受压应变。其表达式为

小组合作学习是一种相对更加自由的学习模式，他需要学生之间自主探索学习、讨论才能达到良好的教学效果。但学生从小受传统教学模式和教学观念的影响，已经习惯于老师的单向填鸭式教育，他们习惯被动地去接受老师传输的英语知识，所以他们在小组合作学习中很难调动起自己的主动性，主动张嘴用英语去交流，有一些学生甚至对小组合作学习采取比较消极不作为的态度，也不积极参与也不积极发言，这样长此以往很容易导致小组学习氛围不佳，影响小组其他成员的积极性，导致小组合作学习效果不理想，提升不了学生的自主学习能力和英语学习成绩。

(10)

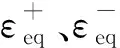
由于混凝土材料的强非线性,依靠完备的塑性理论进行求解较为复杂,在数值实现的过程中需反复迭代求解,不利于实际工程中的应用。参考已有的经验塑性模型的做法[20-21],本文采用文献[21]中混凝土经验塑性修正模型,具体表达形式为

(11)

上述本构损伤演化所需参数均可根据强度等级,参考GB 50010—2010 《混凝土结构设计规范》[19]进行本构参数选取。

2 动力随机反应分析及可靠度计算

2.1 广义概率密度演化方程

在地震作用下,结构往往发生较大的变形,材料性能进入非线性阶段后,可能出现较为严重的损伤和破坏。在隐式求解过程中,由于材性的软化与刚度的退化可能使得刚度矩阵出现非正定的情况,最终导致有限元求解的不收敛。对于地震作用下大变形强非线性的结构有限元求解问题,往往采用显式方式进行求解,其动力方程的一般求解格式为

(12)

式中:M为质量矩阵;C为阻尼矩阵;G为线性或非线性恢复力向量;Γ为激励影响矩阵;F为激励向量。

(13)

根据刘章军等[22]、CHEN等[23]的研究,概率守恒原理对随机事件描述和状态空间描述在本质上是等价的,而随机事件在演化过程中,具有时间和空间的任意性,因此可以推得

(14)

式中:pzΘ(z,θ,t)为随机系统响应的联合概率密度;Z为研究相关的物理量,例如在宏观上可以是内力或变形,如弯矩、剪力、轴力、位移、速度和加速度,也可以是微观上的应力、应变及损伤等。在本文中选用了结构中的最大层间位移角作为概率分布求解的物理量。

从式(14)可以看出,该方程实现了动力随机系统中自由度个数与方程维数的解耦,将多维动力系统表达为一维的概率演化方程。随机源在演化初始为任意形式,无论是内部自身物理参数的随机,还是外部激励的随机,其最终的演化方程不发生改变,因此上述方程被称为广义概率密度演化方程(简称概率密度演化方程)。在本文中随机源来自灌浆缺陷的随机,根据套筒灌浆完全随机的特性,基于GF-偏差进行了代表点的选取,计算每个有限元样本的赋得概率[24]。然后在每个有限元样本计算结果中,提取出结构所有时刻的最大层间位移角,将最大层间位移角的概率代入到式(14)中,即可对概率密度演化方程进行数值求解。为了限制色散现象的发生,本文采用了总变差不增 (total variation diminishing schemes, TVD)格式的差分形式进行数值求解。

2.2 可靠度计算

对于实际工程,常常可根据随机响应的统计量来判断系统是否正常运行或安全。然而,更为科学合理的做法是根据一定的失效(破坏)准则,给出系统可靠性的概率度量,即在概率的意义上定量地评价结构的安全程度。本文选取首次超越破坏为结构失效准则,研究工程结构的动力可靠度问题。

工程结构的动力可靠度定义为在我们所关心的时间内引起结构失效的物理量不超过其安全区域的概率为

(15)

本文选取了层间位移角作为判断结构是否失效的物理量,采用吸收边界条件的方法计算结构的动力可靠度[25-26]。当结构最大层间位移角超出设置的失效阈值时,我们即认为结构失效,该样本的物理响应概率在失效后不再参与到概率密度演化方程中,其表达式为

RzΘ(z,θ,t)=0z∈Ωf

(16)

式中:Ωf=Ω/Ωs为结构失效域。当结构响应超过安全域后,按式(16)对概率边界条件进行吸收,超过安全域后的概率不再回流到方程(14)中进行求解。

(17)

(18)

3 结果与讨论

利用1.3节中介绍的建模流程,批量生成了106个套筒灌浆质量随机缺陷的有限元分析模型,进行了在地震作用下的随机反应分析。

为宏观展示套筒灌浆质量缺陷随机性对结构抗震性能的影响,图8选取了计算结果中部分模型最终时刻的损伤云图,现浇结构计算结果如图8(a)所示,其余模型为套筒灌浆随机缺陷下装配式结构的计算结果。由损伤云图可知,对于套筒灌浆连接可靠的结构(模型1),其在地震作用下具有可靠的抗震性能,能满足“预制等同现浇”的抗震要求。对于套筒灌浆缺陷不明显的结构,损伤主要集中在结构中上部十八层至二十二层左右(如模型3),受损位置基本与现浇结构一致,但损伤区域明显大于现浇结构。对于套筒灌浆缺陷数量较多,且竖向连接性能较差的结构,损伤不再集中在某一处,在结构中上部及中下部都有明显的损伤带,造成了层间位移角的加大(如模型3和模型4)。也有部分模型损伤带扩散,破坏集中在结构主体中部位置(如模型5)。上述结果表明,套筒灌浆的随机缺陷将影响结构的整体非线性行为,其结构响应、损伤位置、破坏形态与套筒灌浆的随机性是相关的,体现了动力作用下复杂高层结构非线性与随机性的耦合效应。

图8 部分模型最终时刻损伤对比云图Fig.8 Damage contrast nephogram of some models at final time

为了定量分析在套筒灌浆随机缺陷的作用下结构的抗震可靠度,选取结构的最大层间位移角作为研究物理量。应用概率密度演化理论,基于TVD差分格式求解广义概率密度演化方程组,获得装配式整体结构在地震作用下的响应概率密度函数演化曲面,如图9所示,其典型时刻概率密度函数的分布如图10所示。

图9 层间位移角概率密度演化曲面Fig.9 Probability density function (PDF) evolution surface of the inter-story drift angle图10 层间位移角典型时刻概率分布图Fig.10 Probability density function (PDF) at typical instants of inter-story drift angle

由图9和图10可知,由于套筒灌浆质量缺陷具有随机性的特性,对地震作用下结构的最大层间位移角产生了较大的影响。在地震荷载的持续作用下,最大层间位移角随着时间发展逐渐增大;此外,套筒灌浆质量缺陷的随机性引起结构反应的差异被逐渐放大,随着时间的推移,层间位移角离散性增加,在地震作用5 s时,由于地震加速度较小,其最大层间位移角较为集中,但在18 s时地震动加速度逐渐达到峰值,其套筒随机性能引起的结构反应离散性逐渐体现。当分析结束时,最大层间位移角离散在0.1%～0.2%这个范围内,变异性达到20%左右,充分说明了在装配式结构中,套筒连接质量对抗震性能的影响。

基于首次超越破坏机制如图11所示,选取每一时刻的最大层间位移角阈值为抗震性能指标(本文层间位移角阈值分别为2.1‰、1.8‰、1.5‰、1.2‰、0.8‰),通过引入吸收边界条件,计算得到结构在不同的层间位移角限值下的结构抗震可靠度。从计算结果中可以看出,在不同的安全域内,结构可靠度有较大的差异,随着限值的增加,结构的可靠度也随之增加。结构可靠度随时间变化的曲线呈阶梯状,说明结构的响应变化不是泊松过程或马尔科夫过程。

4 结论

本文基于某实际工程结构,建立了装配整体式有限元模型,考虑了灌浆缺陷随机性的影响,采用了概率密度演化理论,结合双标量弹塑性损伤本构进行了动力随机反应分析及可靠度计算,计算结果表明:

1)套筒灌浆的质量缺陷将对结构的抗震性能产生较大的影响,由于缺陷的随机性,其结构响应、损伤集中位置、破坏形态都将随套筒灌浆缺陷的程度与位置的不同而有所差异。对于竖向连接可靠的结构,其抗震性能较好,可以实现“预制等同现浇”的抗震目标,论证了保证套筒灌浆连接质量对推广装配式结构应用具有重要的工程意义。

2)在Chi-Chi地震波作用下,当考虑灌浆缺陷随机性时,材料非线性与随机性将相互耦合,将逐渐影响结构响应的随机性,在最后时刻该结构的最大层间位移角的变异性达到20%左右;随着地震的持续作用,结构的层间位移角离散性逐渐增加,表明灌浆缺陷对结构抗震性能的影响会随着地震作用的推移而加剧。

3)采用不同的吸收边界条件,量化分析了某实际工程中装配整体式剪力墙结构在不同安全域内的可靠度,结果表明在不同的层间位移角限值,整体可靠度有较大的差异,随着层间位移角限值的增加,结构的可靠度也随之增加。

高层结构的非线性随机地震反应分析是结构工程与地震工程中具有高度挑战性的核心问题,当前由于工程地震学、随机动力学、损伤力学和计算力学的发展、交叉与融合,使得高层结构的非线性随机地震反应分析与抗震可靠度计算成为可能。而在套筒灌浆连接的装配式结构中,精确的描述缺陷程度的概率分布以及缺陷对竖向连接性能的影响尚需要开展进一步的研究,从而为实现服役工程结构的性能设计奠定基础。