基于改进ISM 的农村自建房防灾韧性影响因素研究*

赵平 刘姝 黄昱豪 朱怡帆 唐明华

（西安建筑科技大学土木工程学院，陕西西安 710055）

0 引言

农村自建房作为自然灾害的重要承灾体，是防灾减灾中极为重要的一部分，使用现状却不容乐观。近年来，农村自建房坍塌事故屡见不鲜，如2020 年8 月山西临汾聚仙饭店坍塌事故，2022 年4 月长沙自建房倒塌事故等，将自建房的质量问题暴露无遗。而我国是自然灾害较为严重的国家之一，灾害种类多、分布广、发生频率高，加之近些年来自然灾害的突发性、异常性和复杂性表现显著，各个影响因素间相互作用耦合，农村自建房面临的风险十分复杂。有研究表明，在自然灾害造成的人员伤亡中，90%以上是由房屋倒塌导致的。只有提高农村自建房的安全性能，减轻房屋建筑在灾害中的损毁程度，才能有效地减少人员伤亡和财产损失［1］。因此，分析影响农村地区自建房安全的关键因素并构建防灾韧性框架，对评估农村房屋灾害损失、做好防灾减灾工作、全面提升我国农村房屋减灾水平有着非常重要的意义。

鉴于此，本文通过实地调研和专家咨询，从自建房可靠性和恢复力2 个维度确定相关影响因素，运用决策实验室法（DEMATEL）对解释结构模型法（ISM）进行改进，应用改进的ISM 分析各因素间的内在联系和耦合关系，得出各因素间层次结构，以期找出农村自建房防灾韧性的关键因素，为我国农村地区自建房屋的安全评定和防灾减灾工作的开展提供理论依据。

1 农村自建房防灾韧性

从灾害系统理论出发，农村自建房防灾韧性是指作为承灾体的自建房在孕灾环境下对自然灾害造成结果的抵抗、吸收以及从这种结果中快速恢复的能力［2］。面对自然灾害冲击，灾害发生前后农村自建房性能可由防灾韧性曲线表示，如图1 所示。图1 中BB1表示自建房受到灾害侵袭后的损坏程度，这主要取决于灾害种类及灾害程度；B1T1代表自建房的可靠性，主要取决于自建房质量及使用程度；B1C代表自建房的恢复路径，主要取决于社会资本和资源的可用性；CC1代表自建房恢复程度，一般要求达到日常所需水平；T1T2代表恢复时间。

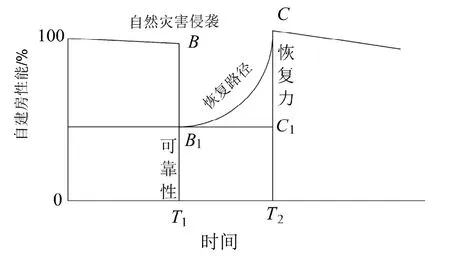
图1 农村自建房防灾韧性曲线

我国农村自建房在建设过程没有统一的执行标准，使用过程中也缺乏严格的监督与管理，使得自建房质量离散性很大，房屋质量远低于城市住宅。而自然灾害的突发性、急剧性和伴生性等特点，使得灾害发生时，较少有控制措施去减轻灾害后果。因此，对于自建房来说，应对自然灾害最有效的方式是提高可靠性，并在灾害发生后及时恢复重建。同时，从灾害中吸取教训，提高自建房韧性。韧性主要取决于可靠性和恢复力，其中可靠性取决自建房本身的强度，恢复力则取决于灾后可获得的资源与帮助。

2 农村自建房防灾韧性影响因素识别

为准确识别影响自建房防灾韧性的关键因素及其作用机理，实地调研了西安市周边具有代表性的村镇，获取西安市周边农村自建房的基本信息。提取可靠性因素10 个（自建房选址x1、楼屋面类型x2、地基基础x3、建筑用途x4、结构类型x5、建造年代x6、建造方式x7、建筑材料x8、墙体类型/厚度x9、是否改扩建x10）；结合我国《自然灾害救助应急预案》、文献查阅及专家经验等，确定恢复力因素13 个（家庭收入s1、常住人口中成年人占比s2、户主受教育水平s3、医疗卫生可得性s4、房屋安全意识s5、资源的外部获得力s6、应急救济s7、物资储备s8、应急避难场所s9、水电供应s10、通信设施s11、住宅加固维修技术s12、灾后组织管理力量s13）。

3 自建房防灾韧性关键因素确认

3.1 DEMATEL-ISM 分析方法

DEMATEL 模型通过分析各因素之间的逻辑关系，利用直接影响矩阵计算出因素间的原因度与中心度［3］。ISM 模型通过建立可达矩阵，可以将关系冗杂的自建房防灾韧性影响因素转化为简洁清晰的层次化拓扑图［4］，明确不同因素间的内在关系与耦合效应。

2种方法的结合具有一定优势。首先，DEMATEL可以简化ISM 的计算过程，2 种方法的分析结果可以互相佐证，其次，DEMATEL 可以丰富ISM 的研究结果，更深层次地分析因素间的影响程度［5］。2 种方法结合能够使农村自建房防灾韧性各因素间的关系更加清晰直观。

3.2 DEMATEL-ISM 模型构建

（1）确定直接影响矩阵。若形成一个考虑所有因素的单一矩阵，该矩阵会变得相当复杂，也不利于专家打分，可能导致结果或关系不准确。为了克服这些复杂性，本文生成了2 个不同的矩阵：一个用于分析可靠性，另一个用于分析恢复力。分别邀请10 位从事土木工程安全施工管理领域和应急管理领域的专家对因子间的作用强度，按没有影响、较小影响、一般影响、较大影响和非常大影响5 个等级赋值为0、1、2、3 和4，表示两因子间相互影响的程度，分别得到10 个可靠性和恢复力的初始直接影响矩阵。为了消除专家打分的主观差异，综合各位专家的意见，将专家打分取平均值得到初始直接矩阵，构建农村自建房防灾可靠性直接影响矩阵O1和恢复力直接影响矩阵O2（由于2 个矩阵计算过程完全一样，故描述时统称为O，下同）。

（2）计算各因素的影响度、被影响度、中心度和原因度。根据式（1）对初始直接矩阵O进行规范化处理得到直接影响矩阵B。

由式（2）计算综合影响矩阵T。综合影响矩阵是指系统因素间直接和间接影响的综合效应。

式中，I为单位矩阵。

影响度指的是T矩阵各行之和，表示各行对应元素对所有其他因素的综合影响值，记为Di。

被影响度指T矩阵中各列之和，表示各列对应要素对所有其他要素的综合影响值，记为Ci。

中心度表示因素在评价体系中的位置及其所起作用的大小，要素i的影响度和被影响度相加即为该要素的中心度，记为Mi。原因度由要素i的影响度和被影响度相减得到，记为Ri，代表各影响因素之间的因果。

由式（1）—式（4）计算得出影响度、被影响度、中心度和原因度，绘制出农村自建房韧性影响因子原因-结果，如图2 所示。

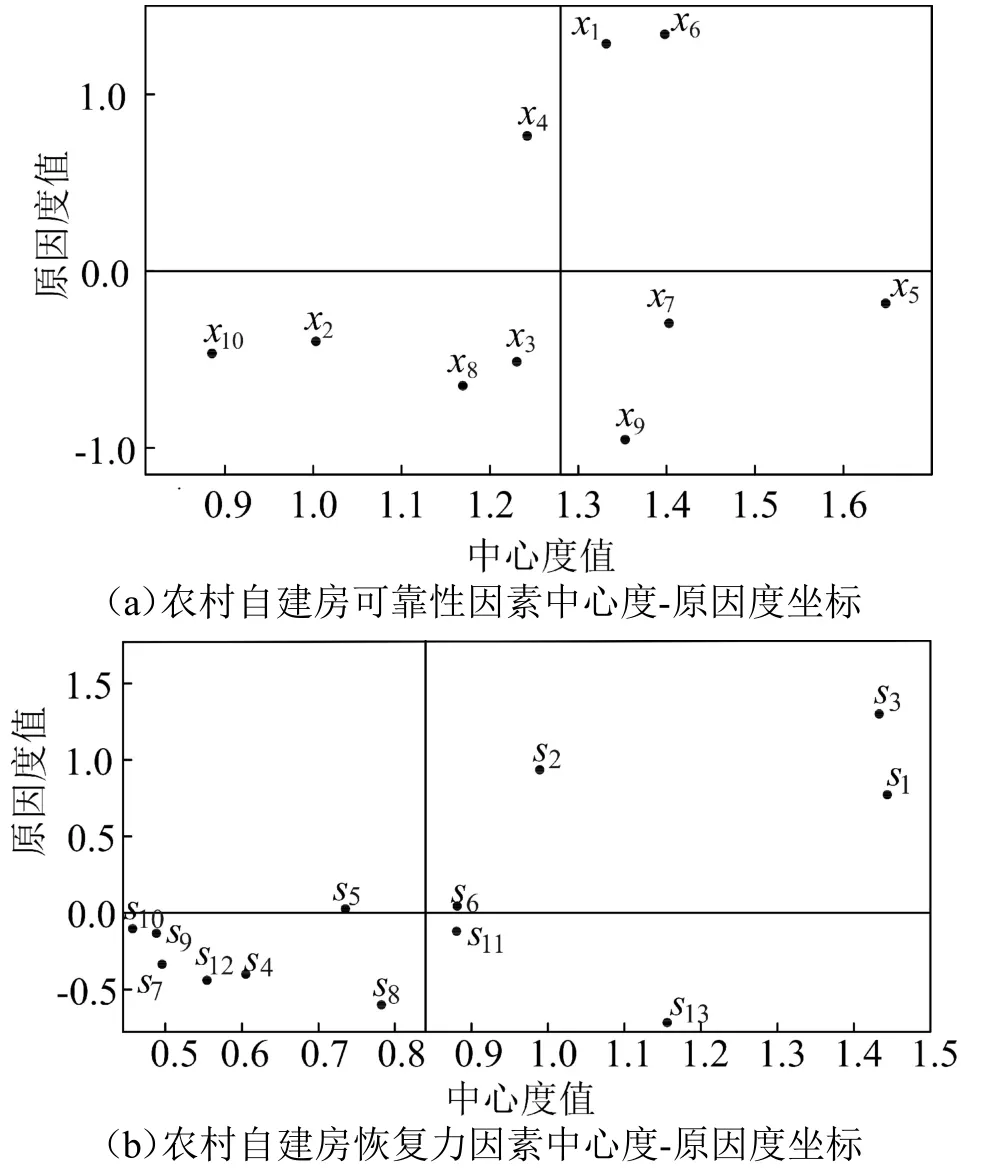
图2 中心度-原因度笛卡尔直角坐标

（3）计算可达矩阵并确定层级结构。将矩阵T转化为邻接矩阵A。为了建立更加简洁有效的层级关系，在最终确定初始影响矩阵之前进行了一些修改。修改主要基于2 个原则：第一，删除因素间的弱连接和间接连接；第二，删去处于同一水平的因素［4］。xi对xj有直接影响的aij为1，反之aij则为0，最终得到邻接矩阵A。通过单位矩阵I与A矩阵相加来计算整体影响矩阵H。

由矩阵B通过连乘或者幂乘直到矩阵不再发生变化得到可达矩阵M。

进而求出农村自建房防灾韧性影响因子的可达集P（xij）和先行集Q（xij）。

若P（xi）∩Q（xi）=P（xi），则xi为当前的最高级要素。

分步找到每一层的最高级要素，这样层层递进就可以将所有影响因素划分层次。因此，可将农村自建房韧性可靠性影响因素划分为5 个层级，恢复力影响因素划分为4 个层级。由于家庭收入会影响房屋结构类型，因此将结构类型（x5）和家庭收入（s1）联系起来，把自建房可靠性和恢复力联系起来形成完整的韧性系统，最终得到的自建房可靠性和恢复力因素影响层次结构如图3 所示。

图3 农村自建房防灾韧性影响因素层次结构

3.3 结果分析

由图2 和图3 可知，在自建房可靠性方面，建造年代（x6）和自建房选址（x1）中心度和原因度均较高，是影响农村自建房防灾可靠性的关键因素，其中建造年代更是深层次影响因素（图3）。而结构类型（x5）、建造方式（x7）和墙体类型/厚度（x9）原因度均为负值，但中心度却较高，因而属于自建房防灾韧性中比较重要的影响因素。地基基础（x3）、建筑材料（x8）、楼屋面类型（x2）和是否改扩建（x10）原因度和中心度均较低，但这些因素一旦出现问题，很可能成为影响自建房防灾韧性的直接因素，如图3 所示。因此应规范自建房建造过程，严格管控违规改扩建行为。

在灾后恢复力方面，家庭收入（s1）、户主受教育水平（s3）、常住人口中成年人占比（s2）和资源的外部获得力（s6）中心度和原因度均较高，是农村自建房防灾韧性中恢复力维度的关键因素，并且对其他因素影响较大。经济基础与户主受教育水平可以为灾后自建房恢复与重建提供更多的思路与选择。而常住人口中成年人占比较低的家庭，在自然灾害发生后需要政府重点关注。通信设施（s11）和灾后组织管理力量（s13）中心度较高，但原因度较低，对自建房灾后恢复力具有较大影响。在自建房防灾过程中，可通过增强居民房屋安全意识和户主受教育水平等其他因素实现对这类因素的间接影响。

4 结论

（1）从韧性角度分析农村自建房应对自然灾害的复杂性，得出农村自建房防灾韧性主要取决于房屋的可靠性和灾后恢复力。

（2）在自建房可靠性方面，结构类型、建造年代和建造方式中心度较高，分别为1.649、1.414 和1.402；在恢复力方面，家庭收入和户主受教育水平的中心度较高，为1.443 和1.435。表明这些是自建房防灾减灾过程中较为重要的因素，容易受到其他因素影响。

（3）在评估农村自建房防灾韧性时应对这些因素重点关注。同时应针对不同类型的影响因素给出相应的控制措施及建议，减轻灾害损失。