大型冷库液氨储罐结构强度计算分析与校核*
王虎强 郑舟斌 刘群芳 温小飞
(1.浙江海洋大学船舶与海运学院,浙江舟山 316022;2.舟山市特种设备检测研究院,浙江舟山 316000;3.浙江国际海运职业技术学院,浙江舟山 316021)
0 引言
液氨因其极高的性价比被国内的大多数制冷企业选择作为制冷剂。但液氨气化后形成的氨气与空气接触后容易形成爆炸性气体,当液氨储罐存在设备老化损坏等方面问题时,就有可能发生泄漏导致爆炸或中毒事故[1]。2013 年6 月,吉林某公司发生重大火灾爆炸事故,引发液氨输送管道爆炸,共造成121 人死亡,同年8 月,上海某公司发生液氨泄漏事故,导致15 人死亡。2016 年10 月,山东某公司脱硫脱硝装置氨水罐发生爆炸,造成5 人死亡[2]。
对于液氨储罐这类压力容器的设计主要有传统公式计算法和有限元分析法。传统公式计算过程无法得到压力容器在工作时的应力分布,主要参照强度设计公式,增加设计时的安全系数确保计算结果的可靠性,所以这种方法很难保证压力容器在工作状态下的安全[3]。有限元分析是基于结构力学分析的计算方法,压力容器受力后的应力分布和变形可以通过有限元软件仿真得出,很容易找出最大应力和应力集中处,从而确保结果的可靠性。陆明万等[4]结合近年来压力容器分析和设计方法的进展,重点介绍了当今压力容器分析与设计的主流方法——应力分类法。唐海峰等[5]采用有限元方法对压力容器的应力分布进行了定性分析,对于具有复杂结构的压力容器更能够保证设备结构强度和安全性。
本文基于有限元方法对液氨储罐的变形与应力分布进行定性分析,同时在应力集中区域进行线性化仿真计算,最后参照《钢制压力容器——分析设计标准》(JB 4732—1995)给出的使用范围和限制,对各应力分量进行了对比与评价[6]。
1 基础理论与方法
1.1 数学模型
一个受力结构内部的任意一点,其应力的分量可以表示为图1 所示的状态。如图1 所示,该结构点处共有9 个应力分量,对于在同一平面上的切向应力,其数值大小是相等的,即xy=yx,xz=zx,yz=zy,因此,实际上只有x、y、z共3 个法向应力和xy、yz、zx共3 个切向应力。旋转应力坐标系后,该点处的应力分量也会改变,因此可以证明,结构内任意一点任意旋转后,总是可以找到使得各切向应力为零的某种状态,在该坐标系下,应力分量只剩x、y、z,将其按数值大小分别命名为:最大主应力、中间主应力和最小主应力[7]。

图1 结构内部任意一点处应力分量示意
在3 种不同主应力作用下,评判材料失效破坏的强度条件时,根据不同的应力强度有不同的理论,机械及力学领域目前主要的四大强度理论如下:
第一强度理论。该理论要求:
该理论认为,无论材料在什么应力状态,只要材料的最大正应力超过了强度极限,即认为材料失效。该理论通常在脆性断裂材料中应用比较广泛。
第二强度理论。又称为最大主应变理论,要求:
这一理论认为破坏主因是最大伸长线应变。不论复杂、简单的应力状态,只要第一主应变达到单向拉伸时的极限值,即断裂。
第三强度理论。又称为最大切应力理论,要求:
这一理论认为破坏主因是最大切应力。该理论在塑性材料的破坏中应用比较多。
第四强度理论。又称作最大畸变能密度理论,要求:
该理论适用于绝大多数塑性材料,应用非常广泛,较第三强度理论更为准确,但形式较为复杂;相比前3 种理论,第四强度理论考虑了复杂应力状态;该理论认为,形状改变比能是引起材料失效的主要原因,无论处于什么应力状态,只要材料的最大畸变能密度超过了强度极限,即认为材料失效,这里的强度极限一般指的是单向应力状态下的极限值[8]。
1.2 原理方法
应力分析的方法来源于薄壳理论和受弯梁,根据应力对整体结构的影响,将应力分为一次应力和二次应力。应力线性化是一种基于板壳理论的强度校核方法,其基于应力分类线,该线通常是截面内外壁两点之间自定义的线段[9]。
根据应力线性化方法,基于等效原理在有限元仿真分析后,总应力被分解为3 种,第一种是在厚度方向分布的薄膜应力,第二种是沿厚度方向线性分布的弯曲应力,第三种是沿厚度方向呈非线性分布的峰值应力[8]。在线性化应力计算中,薄膜应力分量计算公式:
弯曲应力分量计算公式:
峰值应力分量计算公式:
式中,ij为评估点的总应力;ij,m为评估点的薄膜应力分量;ij,b为评估点的弯曲应力分量;ij,F(x)为峰值应力分量。
对于本文所研究的压力容器设备,其应力应满足《钢制压力容器——分析设计标准》(JB 4732—1995),储罐罐体及鞍座的强度限值按照以下规定:①一次总体薄膜应力强度:Pm≤KSm;②一次局部薄膜应力强度:PL≤1.5KSm;③一次薄膜应力加一次弯曲应力强度:PL+Pb≤1.5KSm;④一次局部薄膜应力加弯曲应力加二次应力PL+Pb+Q≤3KSm。式中,Sm为材料许用应力;K为载荷系数;材料许用应力极限Sm=133 MPa。
按照《钢制压力容器——分析设计标准》(JB 4732—1995)中的规定,在应力校核中,载荷组合系数保守取K=1,以便于结果评定[10]。
2 几何模型
以化工行业某大型冷库的液氨储罐作为研究对象,该液氨储罐属于Ⅱ类压力容器,几何简化模型如图2 所示。储罐主要是由椭圆形封头、罐体和鞍座组成,该容器内径为1 400 mm,容器长5 629 mm,罐体和封头壁厚均为14 mm,储罐容积为8.18 m3,容器净质量3 070 kg,液氨充装量为11 250 kg,设计压力2.05MPa,设计温度52℃,耐压试验压力为2.56MPa,产品参考标准《制冷装置用压力容器》(NB/T 47012—2010),工作介质为液氨。储罐底部由鞍座支撑,通过地脚螺栓与地面基础进行固定约束[11]。

图2 液氨储罐外形几何模型
按照《压力容器第1 部分:通用要求》(GB150.1—2011)、《压力容器第2 部分:材料》(GB 150.2—2011)、《压力容器第3 部分:设计》(GB 150.2—2011)、《压力容器第4 部分:制造检验和验收》(GB 150.4—2011),材料的应力强度按照标准《压力容器第2 部分:材料》(GB 150.2—2011)确定,液氨储罐的材料及力学性能参数见表1。

表1 储罐主要材料及力学性能
3 有限元模型
3.1 网格单元
在液氨储罐有限元仿真分析中,考虑到储罐整体尺寸较小,为了提交计算精度,因此储罐整体采用实体单元对其进行网格划分。单元类型是进行网格划分时所使用的单元形式,本文选取的实体单元是SOLID185 单元,该单元为8 节点3 自由度,分别为沿x、y、z方向的平动自由度,适用于薄到中等厚度的实体结构,同时根据其结构特点,利用映射网格建立有限元模型,以获得更精确的求解结果[12]。整体的计算模型中共有83 595 个网格,289 064 个节点。储罐整体模型和网格划分如图3 所示。
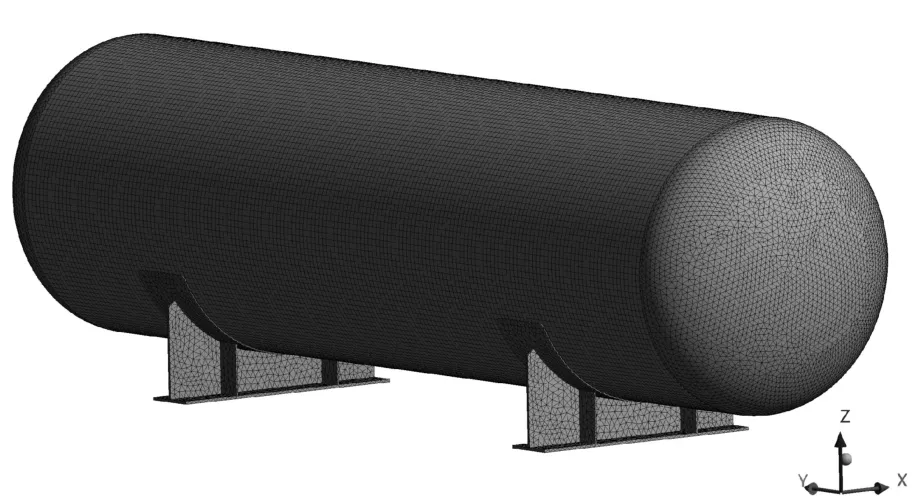
图3 储罐整体模型及网格划分
3.2 载荷及约束
液氨储罐仿真过程中,其载荷及载荷施加方式如下:
(1)储罐自重。储罐总质量为3 070 kg,充装质量为11 250 kg。储罐自身质量通过施加z轴方向质力加速度g实现,方向竖直向下。
(2)液货自重。介质的质量通过均匀分布在储罐封头和罐体上来计算,该储罐的介质充装系数为0.8,根据液货自重压力公式:
(3)压力载荷。旋转壳体承受的载荷是沿容器壁对称分布的,所以这里考虑均匀内压。储罐内部设计压力2.05 MPa,通过对储罐内表面加载来施加。在储罐外表面施加均匀的0.1 MPa 大气压力。
在此次的研究对象中,只有鞍座的底部是完全固定于地面,因此仿真计算中鞍座模型底部进行全约束,其他部位的任何约束均不予考虑。在计算过程中,在固定鞍座底板上的2 个地脚螺栓对应节点处施加UX=UY=UZ=0 的位移约束。
4 结果与分析
4.1 变形分析
储罐Z 方向位移变形分布如图4 所示,罐体与封头连接处附近变形较大,最大变形位移约0.32 mm。因储罐受到均匀的内部压力,罐体内壁均匀向外膨胀,同时储罐外壁受大气压力影响弯曲变形,因此储罐整体变形较小。

图4 储罐Z 方向位移变形分布
为了更加直观地分析罐体的变形,分别在前封头和后封头与罐体连接处、罐体顶端、罐体侧面靠近鞍座处建立了4 条路径,如图5 所示。
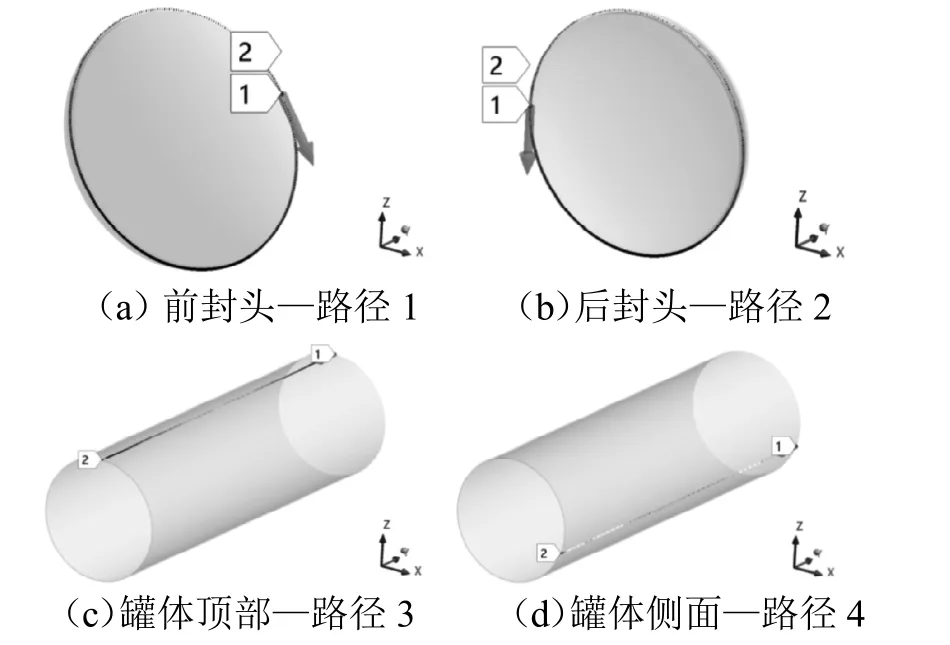
图5 封头与罐体Z 方向形变路径
提取上述各条路径上的位移值,并绘制了封头环向距离和罐体横向距离与变形量关系的曲线,如图6 所示,图6(a)、图6(b)分别是封头环向距离与变形量之间的关系以及罐体横向距离与变形量之间的关系,从图6(a)中可知,封头环向上前封头(路径1)和后封头(路径2)的变形量是呈周期性变化的。封头的顶部与底端变形量最大,而当位于封头的两侧的部位,变形量较小,总体来说,前封头的变形量较后封头的大些。从图6(b)来看,罐体顶部和侧面的变形量相差较大,在罐体顶部(路径3),最大变形处发生在罐体与封头相连的两端区域,变形量约为0.2 mm 左右。罐体中间部位的变形量最小。通过对罐体侧面(路径4)应力线性化分析可知,变形量最小的地方位于罐体两端与封头相连处,随着往罐体中间部位移动,变形量也慢慢增加,但最终变形量趋于0.15 mm 左右。
4.2 应力强度分析
储罐整体的等效应力分布如图7 所示,最大等效应力处位于罐体与鞍座连接的附近,最大等效应力值为143 MPa。

图7 储罐整体的等效应力分布
为了更加直观分析储罐的整体应力,对罐体的顶部与靠近鞍座处的2 条路径进行定量的应力分析,绘制了罐体顶部与侧面两条路径距离与等效应力的对比曲线,如图8 所示。从图8 可知,罐体侧面拉带路径4 的等效应力在靠近鞍座处应力最大,在罐体中间的部位等效应力稳定在90 MPa 左右。罐体顶部拉带路径3 的等效应力在罐体两端处最大,罐体的其他部位整体的等效应力趋于85 MPa 左右。从2 条路径的分析可得出结论,储罐整体的应力集中区域在罐体两端、罐体与鞍座接触附近,罐体中间部位整体应力最低。

图8 罐体线性化路径等效应力数据对比
鞍座与罐体连接局部区域是高应力区,因为计算中采用了实体单元建模,因此在结构不连续的应力集中区域进行应力线性化分析。其中路径的选取原则为:取截面应力强度最大点沿壁厚方向的最短距离,沿垂直于罐体的方向,并在最大应力点处做校准线,最后取每条路径中的最大应力值进行评估。如图9 所示,选择了2 条评估路径。

图9 储罐局部应力线性化分析路径
应力分析结果沿路径5 和路径6 的应力线性化结果如图10 所示[13]。
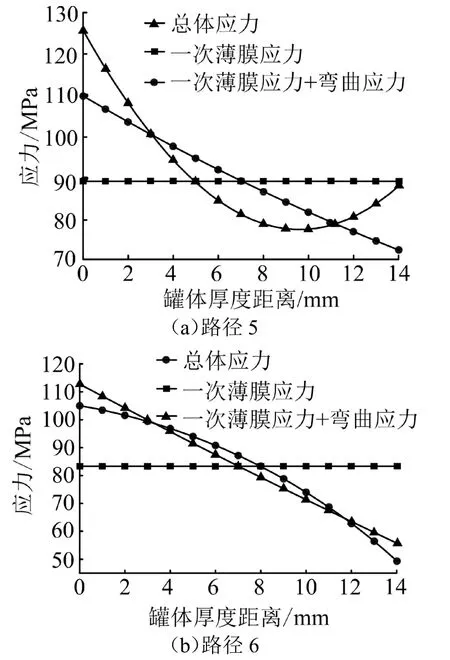
图10 储罐局部应力线性化分析路径数据对比
线性化后路径5的一次薄膜应力值为88.69 MPa,小于许可值133 MPa,一次局部薄膜+弯曲应力为109.87 MPa,小于许可值199.5 MPa;线性化后路径6的局部一次薄膜应力值为83.35 MPa,小于许可值133 MPa,一次局部薄膜+弯曲应力为112.7 MPa,小于许可值199.5 MPa。局部一次薄膜应力加弯曲应力加二次应力最大值为125.67MPa,校核结果均合格。
5 结论
本文利用有限元软件对液氨储罐进行计算仿真,对整体及局部的形变和应力进行数据对比分析,并参照相关标准规定对储罐局部结构的应力进行了强度校核与结果评定。结果表明,液氨储罐在各种载荷组合作用下,各部件的应力均小于规范许用值,局部应力集中区域校核合格,液氨储罐的整体设计满足强度要求。

