高速列车受电弓舱气动外形多目标优化设计

朱陇辉，武振锋，周 琪，霍艳忠

(1.兰州交通大学机电工程学院,兰州 730070; 2.中国铁路呼和浩特局集团有限公司集宁机务段,内蒙古乌兰察布 012000)

当列车高速运行时,其所引发的空气动力学问题与低速时相比复杂程度提高[1]。对于明线运行的列车而言,气动阻力和气动升力是影响其气动性能的两个主要指标[2]。高速列车的气动性能主要取决于其外部形状,但列车的关键部位,如转向架、受电弓导流舱以及风挡等也会对列车的气动性能产生较大的影响[3-5]。对受电弓而言,其整体气动阻力过大会导致列车运行总阻力增加[6]。若受电弓正向气动升力过大,则导致受电弓滑板与接触线磨损严重,负向气动升力过大则会增加列车轴重,进而使轮轨之间的磨损加剧,所以受电弓处的气动升力最理想的状态是使其保持在0 N附近波动[7-10]。

对于高速列车受电弓气动外形优化设计,已有大量学者进行了相应的研究。张亮[11]采用多目标优化理论,对受电弓安装位置和受电弓导流罩进行优化分析,综合考虑多个目标的优化程度对受电弓进行外形优化研究。肖友刚等[12]采用大涡模拟法和FW-H方程对受电弓绝缘子进行外形优化,结果表明椭圆形状的绝缘子降低噪声程度最大。燕永钊等[13]提出了一种新型的受电弓流线型滑板弓头方案,得出该型方案在350 km/h和450 km/h速度下的阻力值,并于原模型在350 km/h的阻力值进行比较,新型受电弓模型整体气动阻力在开口和闭口状态下分别降低25.13%与24.19%。肖守讷等[14]提出两种受电弓导流罩形式,对其进行噪声研究,分别分析了低频段和高频段各导流罩噪声分布,得出最优结构且得到了对未来导流罩的工程化运用有一定指导意义的研究方法。CARNEVALE等[15]研究发现,高速列车运行时受电弓气动升力与列车运行速度有关,气动阻力占列车总气动阻力的8%～14%。HARA等[16]借鉴机翼设计理论,对受电弓滑板进行空气动力外形优化设计,并利用风洞试验验证了优化后滑板外形的合理性。IKEDA等[17]将传统双受电弓改为单受电弓,降低滑板质量来减小弓网磨损,利用此方法来提高受流质量且降低了受电弓整体的噪声。

但是,目前研究人员对于受电弓优化研究多集中于提高其1个气动指标,对多个气动指标综合起来进行优化的研究较少,且关注部位多为受电弓本身杆件外形优化。因此本文从受电弓安装舱形状入手,提出了矩形、椭圆形、胶囊形和六边形4种内置式受电弓舱进行CFD计算,通过优选法得出明线状态下改善受电弓整体气动阻力与升力的最优方案。采用目前研究中应用广泛的多目标优化理论,对优选法下4种受电弓内置式导流舱中的最优方案进行多目标优化,进一步提高受电弓整体的气动性能。

1 气动特性计算结果与分析

1.1 几何模型构建

CFD仿真计算采用常见的3编组模型,由于重点关注受电弓及其附近部位的气动特性变化,故为了提高后期仿真计算的效率,该模型去掉转向架及一些凸出部位。其中,高速列车头车(尾车)长度为27.5 m,中间车长度为25.0 m,列车头部流线形长度为10 m,车辆宽3.3 m,高3.5 m。建立高速列车模型如图1所示。

图1 高速列车模型(单位:m)

在实际运行中,受电弓有升弓和卧弓两种状态。由于受电弓气动升力对于弓网接触的影响在本文的考虑范围之内,故只研究受电弓升弓状态。受电弓模型如图2所示。

图2 受电弓模型

所述4种内置式受电弓导流舱模型如图3所示。从图3可以看出,4种内置式受电弓导流舱模型横向和纵向最大长度一致,深度也相同,但是其轮廓形状有所不同。

图3 4种内置式受电弓导流舱

1.2 计算方法选择

现以列车明线单车运行为仿真模拟工况,速度分别设定为250 km/h和350 km/h。列车最高运行速度为350 km/h,马赫数<0.3,故可认为运行时列车周围空气不可压缩,因此将列车周围流场按不可压缩粘性流场处理。数值模拟计算时采用三维不可压缩Navier-Stokes方程对列车周围流场进行求解,湍流模型采用k-ωSST模型。流场的控制方程为

(1)

式中,ρ为空气密度;φ为流场通量;t为时间;u为流场速度矢量;Г为扩散系数;S为源项。

1.3 计算域及边界条件设定

CFD计算的计算域设定如图4所示,其纵向长度为200 m,横向长度为80 m,高40 m。边界abdc设为速度进口条件,大小及方向与来流速度一致。其中,列车静止不动,以风与列车的相对运动来模拟列车的实际运行;边界efhg设为压力出口条件,为1个标准大气压;边界aegc、abfe和bdhf设为无滑移壁面条件;为更真实模拟列车运行实际情况,将地面cdhg设置为无滑移运动壁面边界条件,速度与来流速度一致。

图4 计算域尺寸(单位:m)

1.4 网格无关性验证

为更好地节约计算资源,在对计算模型进行网格划分之前,需要对计算区域确定合理的网格数量。现对矩形受电弓舱计算模型划分了3套网格,设定进口速度v=350 km/h,模拟计算整车的气动阻力,三套网格的数量与相关计算结果见表1。

表1 网格无关性数据

A套网格数量设为680万,C套网格数量设为1 050万,A与B之间的误差超过3%,但B与C之间的误差小于3%,说明计算区域的网格数量设定在825万个左右是合适的。

1.5 受电弓气动特性计算

采用Star CCM+软件进行计算模型的网格划分和流场计算。划分整个流体计算域的网格时,将体网格最大网格尺寸设为1 024 mm,面网格最小网格尺寸设为8 mm。为提高数值模拟的真实性,需要在列车表面划分边界层,边界层层数为7层,边界层第1层网格距列车壁面的法向距离为0.5 mm,y+值落在30～100之间,网格总数为825万。网格划分完成后,列车纵剖面附近体网格如图5所示,受电弓和导流舱面网格如图6所示。

图5 列车纵剖面体网格分布

图6 受电弓附近面网格

网格划分、边界条件设定完成后,分别进行250 km/h和350 km/h速度下的气动模拟仿真计算。得到受电弓附近表面压力云图和其整体气动阻力与气动升力。其中,350 km/h受电弓附近表面压力云图如图7所示。

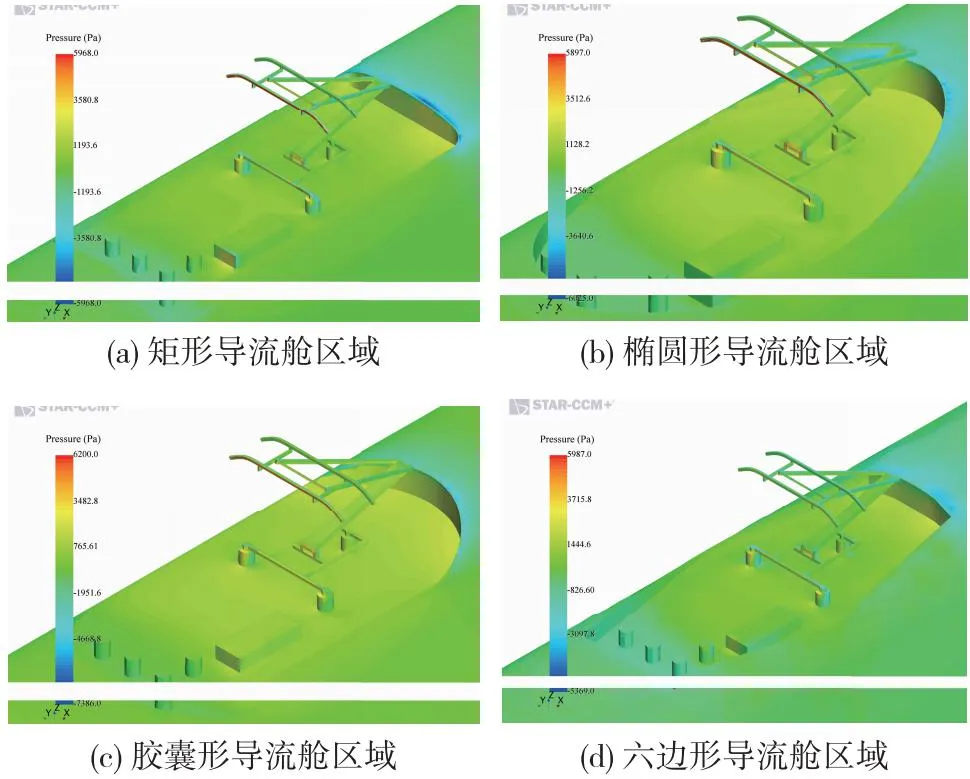
图7 受电弓舱表面压力云图(v=350 km/h)

由图7可知,在高速列车运行过程中,受电弓区域表面压力分布由于其导流装置形状的不同而不同,在该区域,最大正压及负压出现位置类似,但其分布范围明显不同。可以看出矩形导流舱使得受电弓表面压力最小,在导流舱内部压力分布较其他更为均匀。

图8为4种内置式受电弓舱在两种速度级下的气动阻力和升力值,可以明显看出在两种速度级下,矩形导流舱可使受电弓受到的气动阻力与升力最小,因此可以认为4种方案中矩形内置式受电弓导流舱能够最大程度地改善受电弓在高速运行过程的气动阻力与升力性能。

图8 受电弓部分气动力计算值

由于矩形内置式受电弓舱对于受电弓的气动性能改善程度最大,因此对其进行多目标优化,进一步挖掘其潜在的减阻和升力降低效果。

2 多目标气动特性优化

2.1 多目标优化设计理论

提取矩形内置式导流舱主要结构尺寸参数为优化变量,以350 km/h运行时受电弓整体气动阻力和气动升力为优化目标,需采用多目标优化理论,其实质为在非单一目标的情况下,综合考虑各优化变量变化对每个目标的影响程度,使各目标达到综合最优。多目标优化问题的数学模型为[18]

(2)

本文进行多目标优化时采用NSGA-Ⅱ算法进行计算,该算法在优化计算过程中能协调各个目标函数之间的关系,尽可能找出使各个目标函数都满足要求的优化变量解集,简单有效且在计算过程中比较明显。一般情况下,在多目标优化过程中,很难得到一组同时满足所有要求的最优模型,往往一个目标在变优的同时会使得另一个目标性能变差。进行多目标优化研究,最终目的是在各个目标的最优性能之间进行协调与权衡处理,使各优化目标最大程度达到最优值[19-20]。

2.2 优化设计变量选取

在三维建模软件中对矩形内置式受电弓导流舱进行参数化建模,提取主要设计参数为多目标优化的设计变量,矩形内置式受电弓导流舱主要设计参数示意如图9和图10所示,主要设计参数取值范围见表2。

表2 主要设计参数值

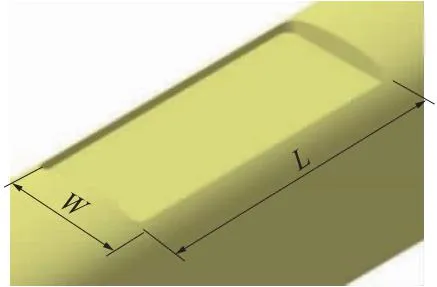
图9 矩形导流舱轴测图

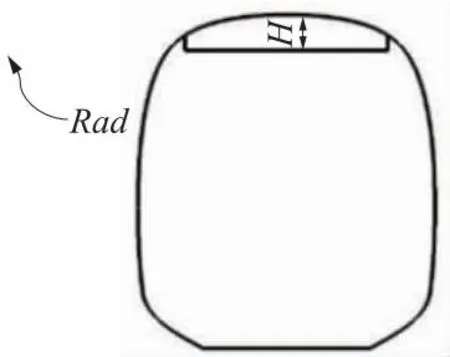
图10 矩形导流舱横截面示意

2.3 近似模型构建

利用参数优化软件Isight,在其中集成软件CATIA、Star CCM+和软件本身自带组件来搭建优化设计流程,Isight软件中搭建的优化设计流程如图11所示。

图11 优化设计流程

采用最优拉丁超立方设计的试验设计方法(DOE)进行样本空间的样本点选取,选取60个随机样本点构建响应面近似模型(RSM),用来代替CFD计算程序进行计算。构建的部分响应面近似模型如图12所示,从图中可以看出,设计变量L和H对优化目标呈线性的影响。响应面模型建立完成之后,应对其进行精度验证。文献[18]中指出,近似模型的精度一般由全相关系数R2决定,R2值越接近1即可认为所构建的代理模型符合要求。现选取其他10组样本值,进行精度误差分析,经过计算得到代理模型R2=0.986,接近于要求值,故认为该近似模型精度符合要求,可用其替代CFD计算程序进行计算。

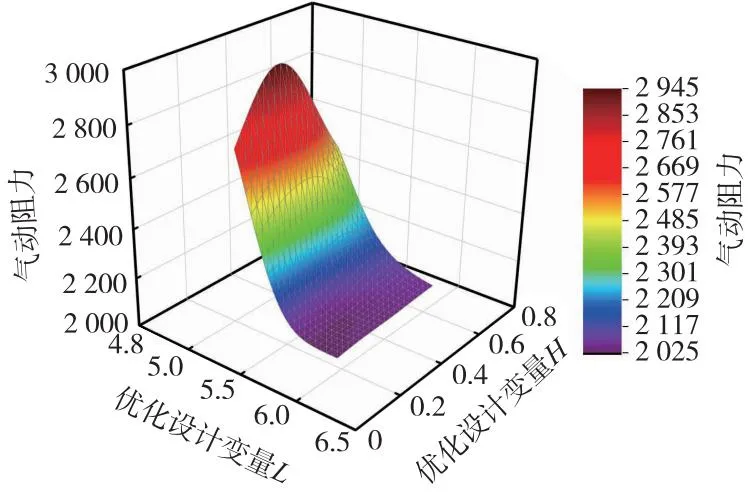
图12 部分RSM响应面三维图

3 优化结果分析

利用已构建的响应面近似模型代替CFD进行计算,参考张亮等[21]针对超高速列车头型进行多目标优化的做法,在Isight软件中选择已经集成的NSGA-Ⅱ算法对矩形内置式导流舱进行多目标优化设计,将NSGA-II算法的初始采样点设定为16个,遗传更新代数设置为20代,共计完成320次的优化迭代计算,完成后可认为矩形内置式受电弓导流舱优化计算完毕。

图13为优化过程中各优化设计变量的迭代历史曲线,可以看出变量L、W、H收敛到了不同的位置,这是由于变量L、W、H不能同时使两个优化目标达到最优,即使得一个目标优化的同时另一个目标变差,而Rad有了良好的收敛值,说明随着Rad的变化,两个优化目标能够同时变优。

图13 优化设计变量迭代历史曲线

图14为设计变量L-Rad与优化目标之间的相关性图,其相关系数范围在[-1,1]之间,图中柱形越高表示设计变量与优化目标相互影响程度越强。各设计变量对受电弓气动阻力影响效应强弱依次为H、W、L、Rad,对气动升力影响效应强弱依次为H、L、W、Rad。其中变量L和H与气动阻力之间的关系为正相关,说明L、H变大会导致受电弓部位气动阻力呈现增大的趋势,而设计变量W和Rad有着相反的趋势。W和气动升力之间的相互关系为正相关,说明设计变量W增加会使得受电弓部位气动升力增大,而设计变量L、H和Rad与W对气动升力的影响相反。

图14 设计变量与优化目标之间相关性

图15为优化过程中各优化目标的优化历史曲线,可以看出在经过320次迭代之后,两个优化目标值都有了收敛的趋势,优化过程中出现的受电弓气动阻力最小可达到1 882 N,表面气动升力最小可达到74.5 N,较初始值气动阻力最大可减小6.5%,气动升力最大可减小2.7%,但需要注意的是最小的受电弓气动阻力和升力值并不是同一组优化变量值所对应的,即两优化目标不能同时达到最优值。

图15 优化目标的优化历史曲线

图16为两个优化目标计算完成后的Pareto解集图,可以看出,Pareto解的空间分布合理,三角形“▲”表示原始模型所对应的气动阻力与升力值,“★”表示优化计算完成后得到的Pareto前沿的最优解。经过对比,可以发现在优化完成之后受电弓的气动阻力和气动升力都有了一定的降低。

图16 Pareto前沿解集

由于优化完成后的Pareto前沿解所对应的一系列优化目标值相差不大,故为使优化目标同时最大程度达到最优,从其中选出了优化模型1～优化模型6。原始模型和优化模型1～6所对应的优化变量和优化目标的值见表3。

表3 Pareto最优解值

从原始模型和优化模型1～6所对应的设计变量及优化目标的值可以得出,受电弓舱长度(L)和深度值(H)变化范围不大,较原始模型变小,受电弓舱宽度(W)较原始模型变大,受电弓舱倾角(Rad)变化范围较大,较原始模型增大,说明受电弓舱往外倾斜有利于改善两个优化目标。优化后受电弓气动阻力最小的是优化模型4,受电弓气动阻力大小为1 894.6 N,较原始模型降低5.9%,受电弓气动升力最小的是优化模型2,气动升力为74.7 N,较原始模型降低2.5%。

4 结论

(1)CFD计算后得出在250 km/h和350 km/h速度时,4种内置式受电弓导流舱中矩形导流舱能够更好地降低受电弓的气动阻力和升力。

(2)构建代替CFD计算程序进行计算的响应面近似模型,模型精度为0.986,能很好地拟合输入与输出之间的响应关系。

(3)采用Isight中集成的NSGA-Ⅱ算法,对矩形内置式导流舱进行多目标优化设计,得到的一系列优化模型能使受电弓气动阻力最大降低5.9%,气动升力最大降低2.5%。

(4)相较于原始模型,得到的优化模型受电弓舱倾角变化较大,较原始模型增大,其余变量变化不大。说明受电弓舱往外倾斜有利于改善受电弓气动阻力和升力性能。