煤矿巡检机器人可变形行走机构设计

李 洋,李 渊,武泽伟

(山西大同大学,山西 大同 037000)

煤矿发生瓦斯爆炸等灾害事故之后,会造成井下机械设备以及运输的矿车发生坍塌、翻转,还会使巷道发生冒顶,堵塞巷道,如地面散落的岩石、煤块的堆积和飘散的粉尘,这种复杂的非结构化环境要求巡检机器人拥有较强的地形适应能力和越障性能。巡检机器人能否完成巡检和环境探测任务的关键在于机器人的行走机构设计,它直接影响机器人在井下的救援工作[1-2]。

因此,针对煤矿井下非结构化的环境和对巡检工作的需求,结合行走机构越障的基本性能,基于平行四边形机构,研究设计一种井下巡检机器人可变性行走机构,代替工作人员进行井下的救援和勘探工作,使其在越障方面具有较高的性能。

1 可变形行走机构整体设计

1.1 常见机器人行走机构

常见的机器人行走机构形式主要有轮式、履带式、仿生式以及复合式等,每种形式的机器人都各有其优缺点。

1.1.1 轮式行走机构

轮式行走机构是工业机器人最常用的行走机构之一,常见的轮式行走机构有二轮、四轮和六轮机构。由于这种机构结构简单,与地面的接触面积小,转向灵活,在较为平坦的路面具有一定的优势。但轮式行走机构对非结构化地形的适应能力较弱,尤其是在翻越障碍物时,翻越的高度受限于驱动轮中心与地面的距离,在障碍物较多的环境当中,行动能力严重受限[3]。

1.1.2 履带式行走机构

履带式行走机构与地面的接触面积较大,对地面压力较小,可以提供较大的抓地力,使其在泥泞湿滑的路面也能保持正常行走,具有较好的越野能力。常见的有双履带、四履带、摇臂式履带等机构。缺点是履带式行走机构相对较为复杂,存在较高的能源消耗和维护成本;且该类行走机构地盘较低,容易出现卡底以及倾覆现象[4]。

1.1.3 仿生式行走机构

仿生式行走机构是模仿动物的运动原理、步态、骨骼结构,以实现更高效的机器人行走能力的行走机构。常见的仿生式行走机构有足式、鸟类、鱼类、蛇类、蜘蛛类机构,优点在于它们在面对复杂的环境都有极强的适应能力,使机器人的行走更加自然、高效。这种机构在探索、农业、医疗、救援等领域具有较为广泛的应用前景。

1.1.4 其它行走机构

除了上述常见的行走机构外,还有各种复合式行走机构。通过将不同类型的机构组合在一起,实现更灵活、多变的行走方式,使得机器人能够在不同环境中具备更广泛的行走能力,以适应复杂的环境,完成多样化的任务。但此类机构存在运动协调难度较大、成本较高等问题[5-6]。

通过对上述各类行走机构的了解,综合考虑各类机器人行走机构的优缺点和对复杂环境的适应能力,使其在越障方面更高效,设计了一种四连杆可变形机器人行走机构,用来进行井下复杂地形的日常巡检工作。

1.2 行走机构整体机构设计

该煤矿巡检机器人行走机构的三维模型如图1所示。该行走机构底盘为轮式机构,分别安装一个电机,控制轮子的运动;左右两侧是对称的平行四边形四连杆机构,连杆之间通过轴连接,前轴装有一个蜗轮蜗杆减速机盒,通过控制连杆机构的运动实现两种模式的切换。

图1 行走机构三维模型

机器人各构件参数如表1所示。

表1 构件参数

2 行走机构运动特性分析

2.1 平行四边形连杆机构位置的不确定性

平行四边形连杆机构在运动过程中的位置存在不确定性,即两曲柄是否会与机架共线、运动过程中曲柄与连杆、上机架是否会发生干涉、上连杆到哪里停止运动。

如图1所示,连杆机构的安装位置为:上连杆平行安装在机架的正上方,两个曲柄平行安装在机架与上连杆的后方,上机架相对曲柄的位置开槽,这样就避免了干涉问题。

如图2所示,当上连杆向后运动到与机架重合时即停止运动,为上连杆与机架重合时的极限位置,此时不会与机架共线,传动角始终大于0°,即不会发生自锁和死点现象。

图2 重合极限位置

由图1可知,平行四边形连杆机构的主动件为前曲柄,共包含4个构件,其中1个构件为固定机架,剩余3个活动构件,共包含4个低副,0个高副,由公式(1)可知:

F=3n-2PL-PH=3×3-2×0-1=1

(1)

式中:F为自由度;n为构件,PL为低副,PH为高副。

自由度F为1,与主动件数量相等。

综上,可知机构有确定的运动。

2.2 越障性能分析

2.2.1 通过障碍物路段

当中途有煤块等障碍物时,平行四边形连杆机构在电机的驱动下,左右曲柄带动整体向前摆动,使曲柄与连杆之间垂直成矩形,可直接通过障碍物,无需转弯、攀爬,节省了时间,如图3所示。

图3 通过障碍物示意

根据车轮的半径以及曲柄的长度,计算出该行走机构能通过障碍物的最高距离为181 mm.

建立如图4所示,以行走机构前轮轴心O为原点的坐标系XOY,对行走机构整体进行受力分析,可得各构件所受的力对O点的力矩平衡方程,如下式:

图4 受力分析图

Ff1+Ff2-G1-G2-G3-G4-G5-G6=0

(2)

(3)

式中:G为各构件的重力,N;Ff1和Ff2为地面对构件整体的临界静摩擦力,N;k为电机盒到O的距离,mm;L为连杆重心到O的距离,mm.

2.2.2 通过狭缝路段

路况较为平坦时,平行四边形连杆机构在电机的驱动下,左右曲柄带动整体向后摆动,在上连杆与机架连杆重合时停止运动,机身整体高度大幅降低,可快速通过狭窄的缝隙,如图5所示。

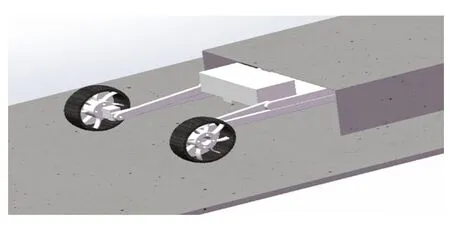
图5 通过狭缝示意

图6为该行走机构通过狭缝时的机构简图。

图6 通过狭缝结构简图

能通过的最小狭缝高度应为:

b+c+d=126 mm

(4)

式中:b为3/2长连杆高度,mm;c为电机盒在长连杆之上的高度,mm;d为车轮半径,mm.

3 机器人倾覆稳定性分析

机器人的倾覆稳定性分析是为了确保其是否可以在不同环境和任务中保持稳定和平衡的重要依据[7]。通过评估机器人在不同地形上的稳定性,可以确保其在各种实际应用场景中不会倾覆或失去平衡。

在此行走机构中,为了适应井下复杂路况,随着平行四边形连杆机构中主动曲柄摆角的变化,机器人行走机构的位姿会随之发生变化,机器人整体的质心分布不断变化,可能会存在质心偏离中心平面的情况,从而产生机器人倾覆的情况。因此,需要对机器人的质心进行求解。

如图7所示,为任意摆角时的机构简图,建立以机器人前轮轴心O0为坐标原点的直角坐标系xO0y.

由图7可得机器人质心O的坐标:

(5)

式中:O为各构件质心;b和k该机构的曲柄和连杆轴心之间的长度,mm;c为电机盒质心O5到前轮轴心O0的距离,mm;d为机体质心O1到前轮轴心O0的距离,mm;α、β、γ分别为机体质心O1、电机盒质心O5、曲柄质心O2与x轴的夹角,°.

将(5)转化后,可得公式(6)。由公式(6)可知,当曲柄向后摆动时,机器人质心O的位置是在以公式(7)为圆心,以公式(8)为半径的圆上,同时随曲柄摆角的变化而变化。但由于曲柄只在0°～90°之间变化,所以机器人的质心只在部分第一象限内的圆弧上变化。

(6)

(7)

(8)

4 结 语

1) 通过对机器人行走机构类型和特点进行对比分析,结合井下复杂环境设计了一种基于平行四边形机构的井下巡检机器人行走机构。

2) 用Solidworks软件建立机器人三维模型,并在障碍物和狭缝两种路况下,对机器人进行仿真模拟和分析,得出机器人通过两种路况的极限高度分别为181 mm和126 mm,结果表明机器人具有更好的越障性能。

3) 通过对机器人的质心位置进行计算分析,结果表明机器人的在变换模式的过程中不会发生倾覆情况,具有较好的稳定性。