考虑气动阻尼影响的海上风电筒型基础整机运行状态振动模拟研究

董霄峰，贾业萌，李文倩，姜军倪，4，周 欢

（1.天津大学 水利工程智能建设与运维全国重点实验室，天津 300350；2.天津大学 建筑工程学院，天津 300350；3.天津城建大学 经济与管理学院，天津 300384；4.长江勘测规划设计研究有限责任公司，湖北 武汉 430010）

在实现“双碳”目标的大背景下，发展海上风电已经成为中国能源结构实现低碳转型的重要途径。筒型基础作为一种新兴的海上风电基础形式［1-2］，凭借其承载力好、建造成本低等优势近年来获得了快速发展，目前已在中国江苏、广东等多个风电场内投入使用。相比于传统的桩基础形式，筒型基础具有基础埋深浅、刚度大等特点，风机运行时叶片旋转与脉动风场相互作用产生的运行激励对整机振动较为敏感，会直接影响结构振动安全。特别是近年来海上风机发生超限振动造成停机的事件屡次发生，海上风电筒型基础整机作为一种振动敏感性结构体系，其动力安全问题也应获得更多关注。

针对海上风电结构的动力安全问题，学者们最先关注的是其在风浪流等荷载联合作用或极端荷载激励下的动态响应情况与疲劳性能。如：王衔等［3］结合广东某场地气象数据，分析了风、浪荷载作用下风机动力响应及疲劳性能；李琪等［4］利用有限元软件建立了大直径单桩与导管架基础的简化模型，分析台风极端工况下风机动态响应；Yan等［5］建立了不同基础形式的海上风机结构模型，对比分析了不同基础形式在风—浪—海流—地震荷载作用下的动力特点。对于运行状态下海上风电结构的动力安全与模拟分析研究，关键是对叶片旋转效应产生气动力或气动阻尼的模拟与施加。现有研究中：李万润等［6］以西北地区某风力发电机为原型，利用数值模拟方法对考虑叶片旋转效应的风电塔架在风—震耦合下的动力响应开展研究；张慧敏等［7］以NREL 的5 MW 海上单桩风机发电机为研究对象，借助叶素动量理论计算叶片上的气动荷载，研究了环境荷载作用下风机运行时结构动力响应；戴靠山等［8］利用FAST软件精确求解叶片气动效应引起的叶轮顶部荷载，分析了风—地震荷载作用下的风电塔筒破坏模式；宋明等［9］基于非线性有限元法和气动阻尼模型，通过数值模拟评估了风荷载与冰荷载耦合作用下单桩海上风力机的动态特性；陈凤云等［10］将气动阻尼以阻尼器形式施加在叶轮顶部，通过数值模拟方法分析了气动阻尼对风机结构动力特性的影响；席仁强等［11］建立了风—地震共同作用的风机简化理论模型，将气动阻尼以阻尼比形式施加，研究了荷载与地震联合激励下风机地震响应；Liu 等［12］建立了风机简化理论模型，将气动阻尼模型纳入时域计算，研究气动阻尼对结构动力响应及疲劳寿命影响。

由上述研究可以发现：现有研究一部分是利用有限元软件与数值模拟方法直接对叶片旋转产生气动力进行模拟，从而达到求解海上风机动力响应的目的，这种方式往往需要较强的计算硬件进行支撑；另一部分研究则是将气动力对振动的影响等效成为气动阻尼的形式，通过在数值或理论模型中施加气动阻尼来实现结构的动力安全分析，这类研究中施加气动阻尼的方式准确与否缺乏实际工程的验证。因此，这里以某海上风电场内1台筒型基础整机为研究对象，考虑气动阻尼效应搭建了整机振动的简化理论模型，研究气动阻尼对运行状态下整机振动的折减效果，并以折减系数形式引入到数值模型计算中再与原型观测结果进行对比，以期为运行状态下海上风电结构振动模拟与安全分析提供一种新的解决思路与方法途径。

1 顺风向振动的理论简化模型

1.1 理论模型

研究对象为海上风电筒型基础整机，如图1(a)所示，在构建理论模型时不考虑叶片与结构之间动力耦合效应，将上部风机和基础部分简化为集中质量，建立等效海上风电结构理论模型，如图1（b）所示。基于欧拉—拉格朗日方程推导风机结构体系运动方程［13］：

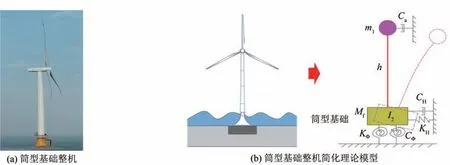
图1 筒型基础整机及简化理论模型Fig.1 Complete machines and simplified theoretical models of the bucket foundation

式中：x为响应向量；f(t)为作用于结构的外荷载向量；M、C、K分别为结构质量矩阵、阻尼矩阵和刚度矩阵。

其中阻尼矩阵C表示为：

式中：Ca是风机的气动阻尼；CH为土体的水平向阻尼；Cϕ为土体的旋转阻尼。CH、Cϕ的计算参考文献［13］。

风机机头的气动阻尼由叶轮旋转产生，能有效降低风机结构的振动响应。在进行顺风向气动阻尼模拟时将风机结构简化为悬臂梁模型，假设外界风速稳定且始终与叶轮旋转平面保持垂直，则作用于单位叶素上的轴向推力可表示为：

式中：W2=V2x+(Ωr)2(1 +a')2；dVx=U(1 -a) -ẋ，其中U为风机轴向风速，ẋ为机舱运动速度；Bb为风机叶片数。

将风机机舱视为单自由度弹簧系统，根据阻尼定义以及叶片桨距角关系，基于上式推导得到风机顺风向气动阻尼为：

第n阶模态的顺风向气动阻尼比ξan表示为［14］：

式中：Mn为第n阶模态质量；ωn为第n阶自振频率。

由于篇幅限制，上述公式中其他参数可参考文献［13］。

1.2 荷载模型

1.2.1 风荷载模拟

瞬时风速包括平均风速和脉动风速两部分：平均风速的周期远离结构自振周期，属于长周期风速，其作用下产生的荷载可视为静荷载；脉动风速周期较短，范围在几秒至几十秒，与结构自振周期较为接近，按照动荷载分析计算。

平均风速的变化采用指数律模型来模拟，表达式如下：

式中：hb、vˉb为任意高度及其对应的平均风速；h、vˉ(h)为标准高度及其对应的平均风速；α为地面粗糙度系数，取0.12。

脉动风速的大小和方向随时间变化，具有随机性和波动性，采用Kaimal 谱［15］作为目标谱结合谐波叠加法进行模拟。

计算塔筒上的风荷载时，将塔筒分为若干段，取每一段塔筒中心高度处的平均风速为该段的风速代表值，每一段上的风荷载视为均匀分布，塔筒整体受到的风荷载以分段集中力的形式施加。风荷载为：

式中：μs为风荷载形状系数，取0.5；μh为风压高度变化系数，按照式（9）计算；V(h，t)为瞬时风速；Ai为第i段塔筒在顺风向上的投影面积。

作用于叶轮上的风荷载采用简化推力系数法模拟：

式中：ρa为空气密度，取1.225 kg/m3；CT为推力系数，由风机厂家提供；R为叶片半径；V为瞬时风速。

1.2.2 波浪荷载模拟

波浪荷载作用于筒型基础过渡段部分，参考《港口与航道水文规范》［16］采用JONSWAP 谱对波浪谱进行模拟，表达式如下：

式中：ω0为波浪频率；H1/3为有效波高，可取为最大波高的二分之一；ωp为峰值圆频率；γ为谱峰升高因子，取其平均值3.3；σ为峰形系数；βJ的计算参考文献［16］。

筒型基础过渡段直径超10 m，置于海流中对波浪场的影响不容忽视。传统方法难以准确计算波浪力，因此参考文献[17]提出的针对筒型基础的波浪荷载计算方法进行随机波浪荷载的模拟。

1.2.3 运行荷载模拟

风机运行荷载包括叶轮质量不平衡和气动不平衡引起的1P荷载和由风切变及塔影效应导致的3P荷载（P为风机转频）。参考文献［18］进行风机运行荷载的近似计算。

假设叶片转速为Ω，对应角速度ω= 2πΩ/60，将叶片不平衡质量简化为偏心质量点，质量为m，其与轮毂中心直线距离为S，与上部风机叶片构成夹角θ。

叶片旋转时不平衡质量点所受离心力Fω为：

忽略重力对偏心质量点影响，引入不平衡质量Im（Im=mS），由1P荷载对泥面产生的顺风向弯矩值反算风机所受1P集中荷载，从而得到顺风向1P荷载表达式为：

式中：b为塔筒中心线离旋转平面的水平距离；H为轮毂距海平面高度；h'为风电场平均水深；Im可参照丹麦2.0 MW Vestas V80海上风机进行估算［18］。

根据3P荷载产生机理，其在顺风向作用与泥面处的弯矩可表示为：

式中：K为下部叶片与重合塔筒部分面积比；L为叶片长度；ρa为空气密度，取为1.225 kg/m3；CD为阻力系数，取0.5；D为塔筒直径；Ua为平均风速，其中Ua（z）=-U(z/H)α，-U为轮毂处的平均风速；z为竖向坐标。

与计算1P荷载思路类似，通过计算3P荷载作用于泥面处的弯矩来反算荷载，得到3P荷载近似表达式：

其中，A为系数［13］。

1.3 考虑气动阻尼后的折减效果

参考气动阻尼的计算理论，分别计算不同风速下的海上风机的气动阻尼，并代入1.1节中搭建的风机结构理论模型，分别计算考虑气动阻尼与不考虑气动阻尼2种工况下塔筒顶部顺风向位移均方根值，进一步计算气动阻尼效应对于结构响应的折减系数，结果如表1所示。由表1可以看出：气动阻尼随着风速的增加呈现增加的趋势，相同风速下考虑气动阻尼对于海上风电结构振动的影响最大可达46.120%，风速越大气动阻尼对于结构振动的影响越明显。

表1 不同风速下气动阻尼及折减系数Tab.1 Aerodynamic damping and reduction coefficient at various wind speeds

2 筒型基础整机数值模型

2.1 三维数值模型建立

这里以某海上风电场内1台3.0 MW 筒型基础为研究对象，利用有限元软件建立与结构等尺寸的三维数值模型，如图2所示。

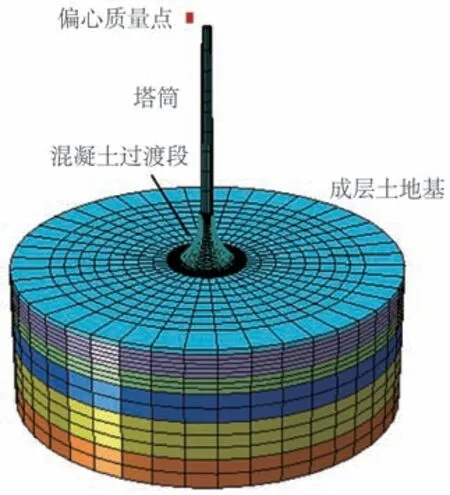
图2 风机整机结构数值模型Fig.2 Numerical models of the complete machine structure

风机结构作为柔性低频振动结构，上部风机对结构振动特性影响不明显，故将上部轮毂、机舱、转子和叶片简化为偏心质量点作用于塔筒顶部。塔筒材料为Q345E 钢，由S4R 壳单元模拟，壁厚48～22 mm。混凝土过渡段、梁结构及顶盖部分采用C60等级混凝土。钢筒及内部分仓板材料为Q235钢。基础部分过渡段和地基为C3D8R实体单元，钢筒为S4R壳单元。为避免混凝土开裂问题，在弧形过渡段内布置2层预应力钢绞线，由T3D2 桁架单元模拟。除预应力筋和过渡段为嵌入连接外，其他结构接触均采用Tie 连接。基础底部采用全约束，侧向采用反对称约束，在该模型所在海域地质条件下，层状地基弹性模量与压缩模量的转换系数在［5.6，6.0］区间内［19］，这里转换系数取为6.0。各层土体参数见表2。结构阻尼采用Rayleigh 阻尼形式施加，材料阻尼比参考文献［20］。对结构进行数值模拟时，环境荷载计算与理论模型中荷载计算方法保持一致。

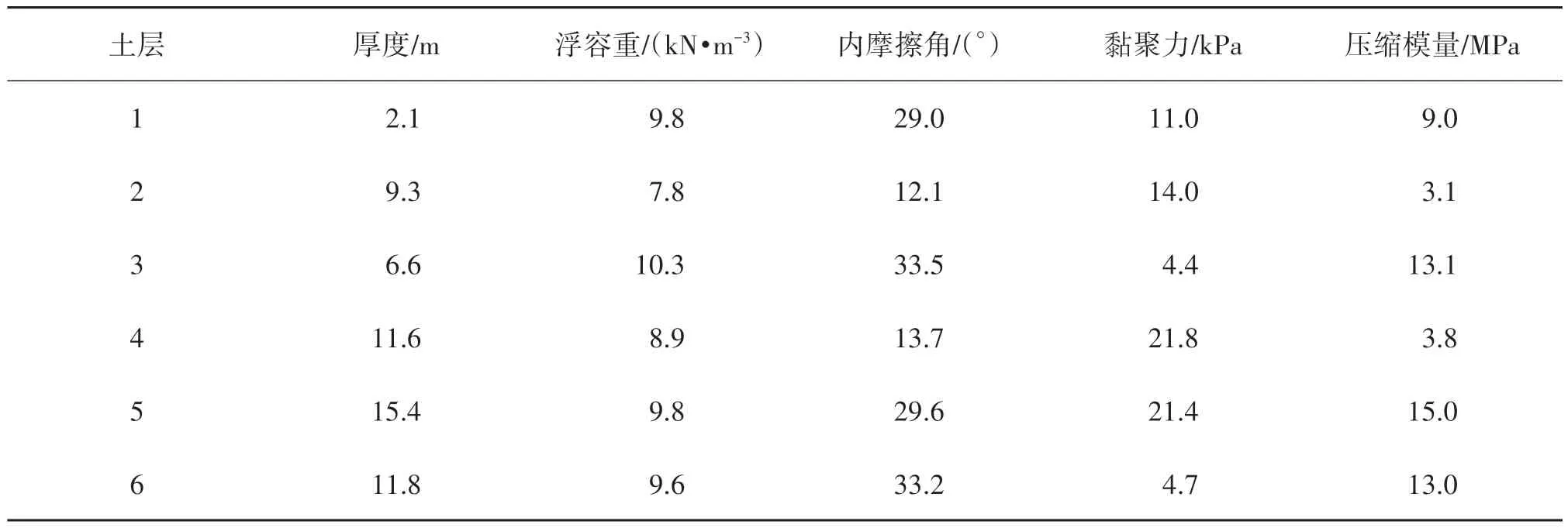
表2 土体参数Tab.2 Soil parameters

2.2 模态分析与共振校核

对海上风电结构数值模型进行模态分析，获得结构前3阶自振频率见表3，对应振型如图3所示。

表3 结构自振频率Tab.3 Natural frequency of the structure

图3 结构振型图Fig.3 Structural vibration mode diagrams

由图3可知：结构每一阶模态对应的2个振型图成对出现，且弯曲方向相互垂直；结构的前3阶振型均表现不同方向的弯振；作为大长细比、高柔度结构，海上风机结构易受到低频荷载激励的影响。当风机结构固有频率接近甚至达到环境荷载激励或叶轮过浆频率时，会产生共振现象，造成结构应力和变形增大，影响风机正常运行。为避免共振现象发生，DNVGL 规范规定［21］，风机结构基频要避开1P、3P前后10%的共振危险频带区域。由风机厂家提供的运行参数可知：所研究风机正常工作转速范围为8.5～12.6 r/min，考虑±10%安全余量后1P、3P共振区间如图4所示。从图4中可以看出风机结构的第一阶固有频率避开了可能引起共振的危险频带区域，满足安全运行要求。

图4 共振分析Fig.4 Resonance analysis

2.3 理论与数值模型对比

由于有限元软件在模拟叶片旋转效应产生的气动阻尼方面存在局限，导致数值模拟结果往往与实际情况偏差较大。为保证结果的合理性，现借助理论模型在考虑气动阻尼时对结构响应的折减效果对数值模拟的振动进行相应折减，从而在数值模型中实现气动阻尼对结构振动响应的削弱作用。在计算折减系数前，需要分别从时域与频域角度对数值模型和理论模型进行对比，以保证两种模型动力特性一致，该折减方法切实可行。

利用两类模型计算仅考虑结构阻尼时不同运行风速下风机塔筒顶部位移的均方根值，并进行对比，如图5所示。结果表明：2种模型下风机塔筒顶部位移均方根值均随着风速增加而增大，结构响应变化规律相似，且达到8 m/s 风速以后，两类模型在同风速下的振动差值稳定在4 mm 左右，证明两类模型在动力学上具有很好的同步性。

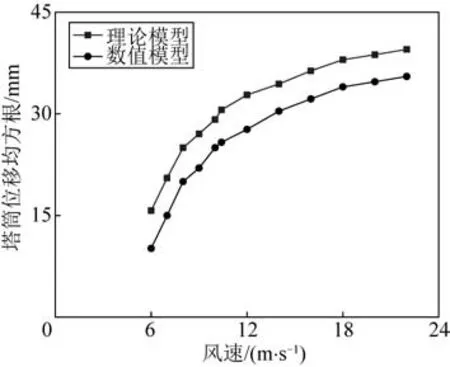
图5 2种模型下风机振动响应Fig.5 Vibration responses of the tower under two models

再通过对所搭建的理论模型进行模态分析，求得前两阶自振频率，并与2.2节中数值模型计算的前两阶自振频率进行对比，结果如表4所示。由表4可知：理论模型与数值模型的整机结构前两阶自振频率误差均小于3%，二者极为接近，证明在频域内理论模型与数值模型动力特性基本一致。

表4 理论模型与数值模型自振频率对比Tab.4 Comparison of natural frequencies between the theoretical model and numerical model

3 振动模拟与折减对比步骤

针对数值模拟方法难以准确模拟叶轮旋转效应产生的气动阻尼，从而导致计算结果与实际存在偏差的问题，引入筒型基础结构理论模型考虑气动阻尼时结构响应的折减系数，对数值模拟结果进行相应折减，以实现考虑气动阻尼影响下海上风电筒型基础整机运行状态振动的准确模拟，具体步骤如下：

1）当叶轮转速为0 时，利用1.2 节荷载模型计算风机所受环境荷载，直接施加到结构有限元模型进行动力计算，提取结构停机工况下的振动响应；

2）当叶轮旋转时，基于1.2节荷载模型计算运行工况风机所受荷载并输入到结构理论模型，分别计算考虑气动阻尼与不考虑气动阻尼2 种工况下风机塔筒顶部位移响应，并进一步计算气动阻尼效应对结构响应的折减系数；

3）将步骤2）中输入的运行荷载施加到风机结构有限元模型，计算得到不考虑气动阻尼效应的结构振动响应；

4）利用步骤2）计算得出的气动阻尼对结构振动响应的折减系数，对步骤3）中提取的结构响应进行折减，实现考虑气动阻尼效应的海上风电结构整机振动模拟；

5）将折减后的数值模拟结果与原型观测值进行对比，验证模拟精度。

4 原型观测与数值模拟对比

4.1 原型观测

所选筒型基础海上风机位于中国黄海海域，整机结构选取5 个测点布置传感器，监测点分布以及塔筒处传感器安装位置如图6 所示。由图6 可知：基于停机工况风机振动位移识别的结构一阶自振频率为0.35 Hz，与数值模型和理论模型的一阶自振频率都非常接近，证明两类模型均具有良好的工程适用性。

图6 风机监测布置及振动频谱Fig.6 The monitoring system layout and spectrum diagram

4.2 停机工况

风机顺桨停机时仅受环境荷载作用，将风机塔筒分为9段，风荷载简化为9个集中力分别施加于各段塔筒，波浪荷载和海流荷载也以集中力形式作用于混凝土过渡段部分。停机工况计算轮毂处平均风速4～12 m/s共9组工况下结构的动力响应，动力模拟时长取150 s，采样频率10 Hz。图7～10分别为轮毂处平均风速为5和11 m/s工况下环境荷载和结构动力响应时程图。

图7 风速5 m/s时结构荷载时程图Fig.7 The load time history diagram at 5 m/s wind speed

图8 风速5 m/s时塔筒顶部振动响应Fig.8 Vibration responses of tower top at 5 m/s wind speed

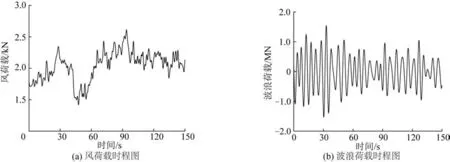
图9 风速11 m/s时结构荷载时程图Fig.9 Load time history diagram at 11 m/s wind speed

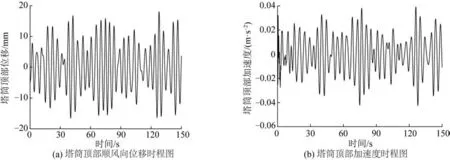
图10 风速11 m/s时塔筒顶部振动响应Fig.10 Vibration responses of tower top at 11 m/s wind speed

各风速下塔筒顺风向位移均方根值与实测值对比结果见表5。由表5可知：停机工况下塔筒位移均方根值均随风速的增加而增大；数值模拟与原型观测的最大误差为13.74%（平均风速为11 m/s 时），平均误差为12.19%，在误差合理范围内［22］，说明建立的数值模型对风机停机状态的模拟合理可靠。

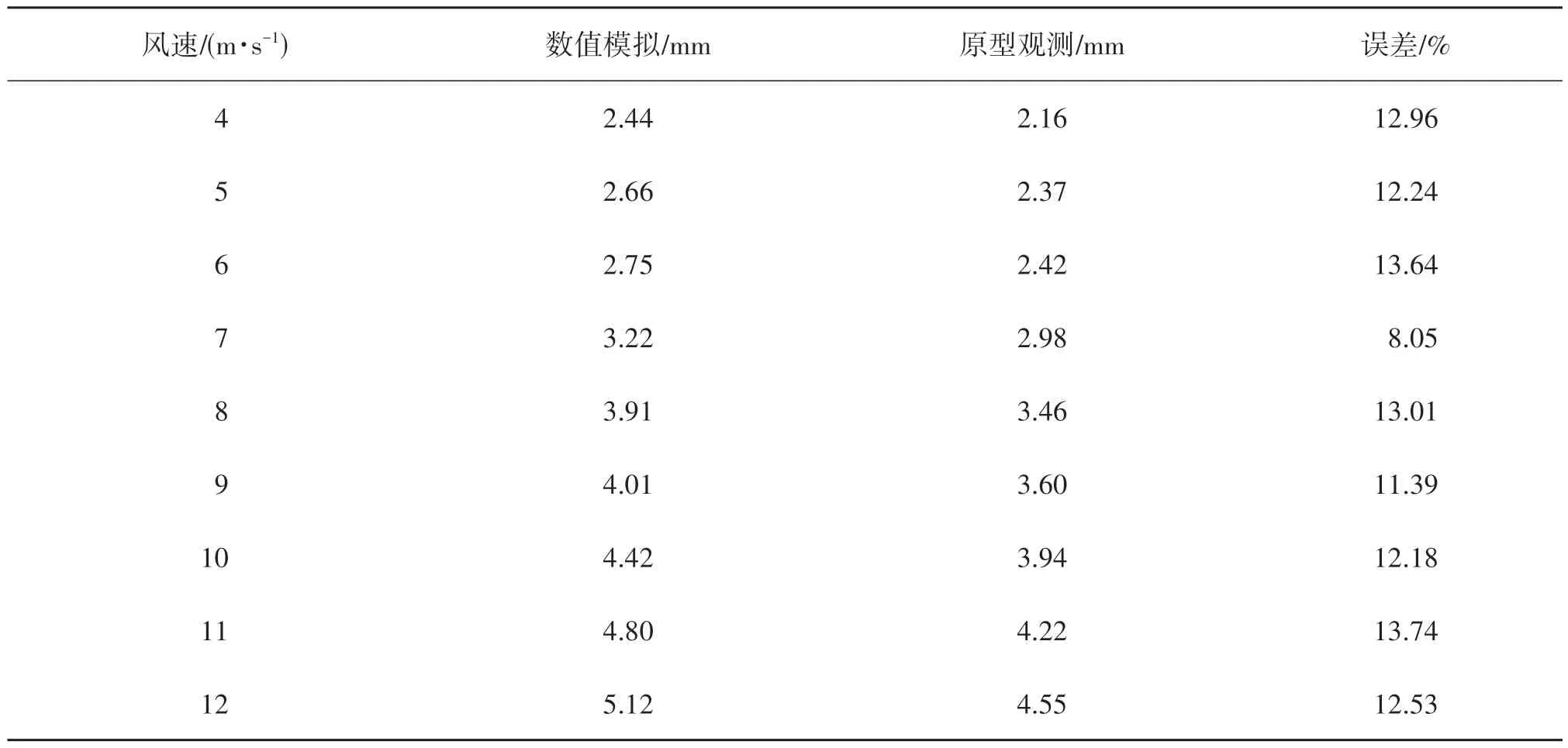
表5 停机工况塔筒顶部位移均方根值数值模拟与原型观测数据对比Tab.5 A comparison between the root mean square values of numerical simulation and prototype observations for the displacement at the top of the tower under shutdown conditions

4.3 运行工况

运行工况下叶片受到的气动荷载是引起风机振动的主要原因，作用于塔筒的风荷载对风机振动影响很小，不予考虑［23］，仅考虑叶片推力、运行荷载及波浪荷载。假定风荷载与波浪荷载作用方向一致，均与机舱方向相同，计算平均风速4～12 m/s区间内的结构动力响应，动力模拟时长取150 s，采样频率10 Hz。图11～14分别为轮毂处平均风速为5和11 m/s工况下风机叶轮所受轴向推力、气动荷载以及结构响应时程图。

图11 风速5 m/s时风荷载时程图Fig.11 The wind load time history diagram at 5 m/s wind speed

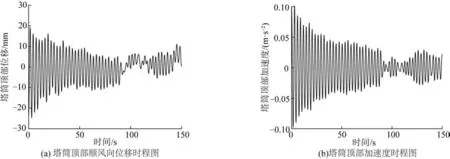
图12 风速5 m/s时塔筒顶部振动响应Fig.12 Vibration responses of tower top at 5 m/s wind speed

图13 风速11 m/s时风荷载时程图Fig.13 The wind load time history diagram at 11 m/s wind speed

图14 风速11 m/s时塔筒顶部振动响应Fig.14 Vibration responses of tower top at 11 m/s wind speed

在数值模型中对结构进行不同风速下的动力模拟，提取塔筒顶部顺风向位移均方根值，利用理论模型计算的折减系数进行折减，并与实测值进行对比，计算结果见表6。

表6 运行工况下塔筒顶部位移均方根值数值模拟与原型观测数据对比Tab.6 A comparison between the root mean square values of numerical simulation and prototype observations for the displacement at the top of the tower under operationg conditions

由表6 的计算结果可知：结构位移响应与风速成正相关，塔筒顶部顺风向位移均随风速的增加而增大；考虑气动阻尼对结果的折减后，运行工况下，数值模拟结果与原型观测最大误差为10.19%（平均风速7 m/s时），平均误差为7.99%，在误差合理范围内［22］，说明基于理论模型对数值模拟结果进行折减的方法是可行的，对海上风机运行工况的振动模拟能够满足精度要求。

5 结 语

以某海上风电场内1台筒型基础整机为研究对象，搭建考虑气动阻尼的整机结构简化理论模型，研究气动阻尼对结构振动的折减效果，并引入数值模型开展考虑气动阻尼影响的风机运行状态振动模拟与原型观测对比研究，得到主要结论如下：

1）简化理论模型与数值模型的整机结构前两阶自振频率误差小于3%，且两类模型的一阶自振频率与实测数据反馈值也极为接近，证明两类模型均与实际工程等效，具有良好的工程适用性。

2）简化理论模型与数值模型的结构振动响应变化规律一致，且达到8 m/s风速以后同风速下振动差值稳定在4 mm左右，证明两类模型在动力学上具有很好的同步性。

3）停机工况与运行工况下，模拟塔筒顶部振动位移均方根值与原型观测值平均误差分别为12.19%与7.99%，说明基于考虑气动阻尼效应的振动理论模型对数值模拟结果进行折减是可行的，精度可以满足工程需求，可为运行状态下海上风电结构振动模拟与安全分析提供一种新的解决思路。