基于CAE-TSNE 的成品油管道运行工况识别

郑坚钦 ，杜渐，梁永图*，赵伟，王昌，丁鹏，吴全

1 中国石油规划总院，北京 100083

2 中国石油大学(北京)机械与储运工程学院，北京 102249

3 浙江大学浙江省饮用水安全与输配技术重点实验室，杭州 310058

0 研究背景及研究意义

成品油管道运行时，由于各个站场泵、阀门等设备运行状态的改变，管道运行工况会随之发生变化[1]。站场调度员根据压力、流量等运行参数的变化趋势来判断工况的切换。由于长输管道呈网络化、智能化发展，且运行工况数据具备多维度、连续时间的特点，其变化情况较为复杂，工况切换较为频繁，因此对管道进行人为监测分析变得越来越困难。另外，人为识别监控效率较低、耗时耗力，且容易对运行工况产生误判。若能基于现场实时运行数据建立工况识别模型，当数据模型的识别工况与现场制定工况不同时，即数据模型识别不准确或现场出现意外工况。因此，对管道运行工况的准确识别开展研究是十分有必要的[2]，识别模型可验证管道运行工况是否符合制定工况类型，可预防管道运行中出现异常工况变化，如泄漏、甩泵等，从而保障成品油管道的高效、安全管理。研究难点可总结如下：

(1)由于人为操作以及泵、阀门等设备的不平稳运行导致的噪声信号会影响管道运行工况的识别分析[3-4]；

(2)管道运行工况数据包含各个站场的进出站压力、流量等数据，数据维度大，分析较为困难。

目前，部分学者对管道运行工况识别进行了研究，如李传宪等[1]利用环道装置模拟出的5 种管道运行工况，基于核的主成分分析法对时频域特征进行降维，基于遗传算法和粒子群算法优化的神经网络对管道运行工况进行识别。余东亮等[5]选用局部投影降噪法并结合小波包分析技术对管道负压波信号进行降噪处理并提取特征值，再对工况进行分析识别。龚骏等[6]通过计算包括泄漏在内的四种工况下压力波的时域特征，降维后基于RBF神经网络对管道泄漏工况进行识别。张宇等[7]提出了基于混沌理论中的关联维数对管道泄漏进行识别的方法。陈志刚等[8]提出了基于多元支持向量机的管道泄漏工况检测方法。Ye等[9]利用管道压力数据，通过小波变换去除噪声，提取时域特征，然后基于模糊c均值算法对管道运行工况进行识别。Zhang等[10]采用动量项梯度下降算法和自适应学习率优化后的BP算法对管道运行状态进行识别。Rai等[11]提出了一种基于多尺度分析、Kolmogorov-Smirnov(KS)检验和高斯混合模型(GMM)的基于健康指数的方法来确定管道泄漏和正常情况。Zhang等[12]基于混沌特性，利用动态压力变送器的管道信号，提出了一种识别管道正常状态和泄漏状态的方法。

虽然目前的识别方法对小批量的工况能够达到较高的精度，但还存在以下几点不足：

(1)管道运行工况的识别主要是针对泄漏工况开展研究[13-16]，建立管道运行工况识别模型的研究较少；

(2)分析识别的工况种类较少，如输量变化、启泵、泄漏等，无法满足现场多工况运行的实际工程需求，如油品切换；

(3)主成分分析(PCA)等线性降维方法对于非线性的管道运行数据适用性较差。

随着人工智能算法和数据挖掘技术的迅速发展，基于现场实际工业过程数据的数据分析方法逐渐成为状态检测技术的研究热点之一。管道的频繁操作会使管内产生瞬变流场[17]，引起单一时刻的运行数据波动。由于管道运行具有连续性的特点，为克服瞬变扰动对于运行工况分析的影响，考虑管道运行数据的时间序列和物理空间特性，本研究综合分析各站进出站流量、压力等参数，选取小段时间的运行数据构造成样本矩阵。

主流的小波去噪方法对于阈值的依赖程度较高，需要多次试验以得到合适的阈值[18-21]。卷积自编码器(CAE)作为一种无监督算法能准确提取数据潜在特征[22]，其通过引入数据特征的稀疏表达，将冗余的信息压缩并表达为稀疏的仅保留有效信息的运行数据，过滤掉其中的噪声成分[23]。CAE作为一种深度学习算法，目前在语音识别、计算机视觉，自然语言处理等许多工程领域都得到了广泛的应用[24]。传统线性降维方法如PCA对非线性的管道运行数据矩阵处理效果欠佳。而基于T分布的随机邻域嵌入(T-SNE)是一种非线性降维可视化方法，对于复杂的高维数据拥有良好的降维聚类效果[25-27]。

针对目前研究的不足，本文基于SCADA数据，构建运行数据矩阵，利用CAE对矩阵数据降噪处理，构建基于T-SNE的管道运行工况识别模型。研究思路如图1 所示：

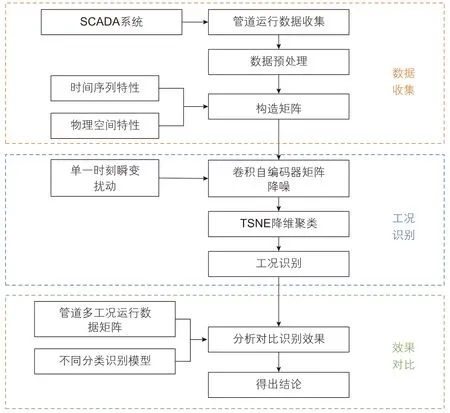
图1 研究流程图Fig. 1 The flow chart of research

(1)基于SCADA系统，对管道运行数据进行收集与预处理，考虑时间序列与物理空间特性，将各站运行参数(压力、流量、密度)构造为二维矩阵；

(2)管道的频繁操作会使管内产生瞬变扰动，利用CAE对矩阵数据进行降噪处理；

(3)利用T-SNE算法对降噪后的矩阵数据进行降维聚类，实现运行工况的准确识别；

(4)对比目前常用的分类算法(ANN、DT、RF)，进一步验证本文的工况识别模型的准确性和有效性。

1 运行工况识别模型

1.1 运行数据的矩阵构造

考虑管道的物理空间特性，将管道划分为多个子单元(包含首站、1 个中间站、末站)，整理运行参数(流量、压力、密度)，包括首站的出站流量、压力，中间站的进出站流量、压力，末站的进站流量、压力，以及各站的密度，共11 个运行参数。SCADA系统间隔5 s提取一次数据，考虑管道运行的时间序列特性，将一段时间(1 min)的运行数据构建为矩阵形式，可得到12×11 的管道运行数据矩阵，如式(1)所示。其中Q为流量，P为压力，ρ为油品密度，上标数字代表不同的站场(A为首站、B为中间站、C为末站)，下标t代表不同时刻。

1.2 基于CAE的管道运行数据降噪

由于管路和泵的振动、管内阀门或者弯管引起管内流体状态改变以及阀门的突然开闭引起管内压力突变，管道内会出现不同程度的噪声[28]。为了降低噪声对工况识别的影响，本文针对管道运行数据矩阵，将构建基于CAE的矩阵降噪模型。CAE基于自编码网络引入卷积操作，通过学习数据的卷积与反卷积映射关系，从含噪声的管道运行数据中提取有效的数据信息。

如图2 所示，基于CAE的降噪过程如下：首先通过编码层1，进行卷积核尺寸为3×3、卷积个数为32的卷积操作，进行步长为2 的池化操作；同理，根据之后各层卷积核尺寸大小、卷积个数以及池化步长进行相对应的先卷积后池化操作，即可完成编码，此时网络得到了输入矩阵的潜在特征，尺寸为1×1×8。随后通过解码层1，进行卷积核尺寸为3×3、卷积个数为8 的反卷积操作，并经过步长为2 的上采样层；同样地，根据后续各层卷积核尺寸、反卷积个数以及上采样步长进行相应的反卷积和上采样操作，网络可将矩阵特征尺寸还原为12×11×32。最终通过输出层将卷积核个数映射为1，得到尺寸为12×11×1 的降噪数据。考虑Adam优化算法基于随机梯度下降法，且对每个不同的参数设定独立的自适应学习率，对于大批量数据的深度学习算法具有良好的优化能力[23]，因此选用Adam优化算法进行迭代训练。

图2 卷积自编码器网络结构Fig. 2 Structure of convolutional encoder network

1.3 基于T-SNE的管道运行数据聚类

优良的数据降维方法是准确提取管道运行矩阵数据潜在特征的关键。相较于目前主流的PCA、Kpca以及SNE降维聚类算法，T-SNE对于非线性的管道高维数据矩阵表现出更为优良的聚类效果[27]。目前T-SNE算法还未在管道运行工况识别领域运用，基于T-SNE的管道矩阵数据聚类的具体步骤如图3 所示。算法流程如下：

图3 基于T-SNE的管道数据聚类流程Fig. 3 The process of pipeline data clustering based on T-SNE

(1)设管道运行数据矩阵为X=(x1,x2,...,xn)，所需得到的运行数据二维空间分布为Y=(y1,y2,...,yn)；

(2)基于管道矩阵数据的条件概率分布计算矩阵数据之间的联合概率分布；

(3)可得矩阵数据的低维空间初始解Y(1)；

(4)计算低维空间管道运行数据间的相似度；

(5)优化数据矩阵对应概率分布与低维空间数据对应概率分布间的距离；

(6)基于迭代得到梯度下降值，求得低维空间下管道运行数据解Y(t)；

(7)当迭代次数达到设定次数后，输出管道运行数据的二维空间表达Y。

1.4 数据预处理

本文选取最大—最小化(max-min)方法对管道运行数据进行归一化处理。假设管道运行数据序列为X={x1,x2,...,xn},对每一个x做如下的处理：

其中，xmin是原管道运行数据序列中x的最小值，xmax为数据序列中x的最大值。

1.5 模型评价指标

本文通过准确率(Accuracy，ACC)表示识别模型的准确度，即分类正确的样本个数占总样本数的比例。实验中各类工况的样本个数较为均衡，使用准确率能够直观的反映模型的分类效果，如式(3)所示。

式中，nc为识别正确的样本个数，nl为用于识别的总的样本个数[29]。

2 算例分析

本文基于某两条成品油管道的SCADA系统数据，整理各站的运行参数。基于1.1 构造运行数据的二维矩阵，引入CAE做降噪处理。矩阵降噪后的部分参数效果对比如图4 所示。可以看出CAE可克服异常扰动点对网络学习的影响，在改善数据平稳性的同时，消除原始数据中的异常点。

图4 卷积自编码器降噪结果对比Fig. 4 Comparison of noise reduction results of convolutional autoencoder

两条管道的基本运行工况包括：停输、启输、停泵、启泵、切泵、分输以及油品切换，结合管道调度中心操作日报，可提取各工况对应的管道运行数据，并对每种工况进行编号，工况种类如表1 所示。

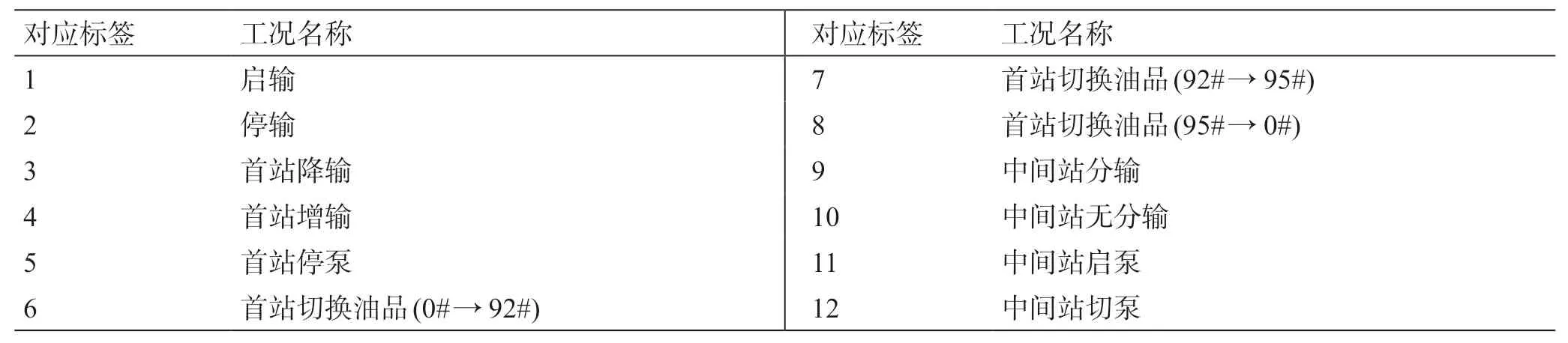
表1 工况种类对照表Table 1 Comparison table of working conditions

以表1 各个工况的运行数据为例，基于CAE降噪处理后，通过T-SNE降维聚类，并对比PCA的聚类效果。从图5 的聚类结果可以看出，T-SNE的聚类结果比PCA更为显著，同一工况的数据点集中在一起，而在PCA中，不同工况的数据点会相互重叠，聚类效果不佳。在图5 中，横纵坐标轴分别代表一个主成分。T-SNE对管道运行工况的识别准确率如表2 所示，可以看出对于降噪前的工况数据，中间站启泵以及分输的识别准确率较低。而利用CAE进行数据降噪后，T-SNE的整体聚类识别效果显著提升，工况的平均识别准确率都能达到99%以上。

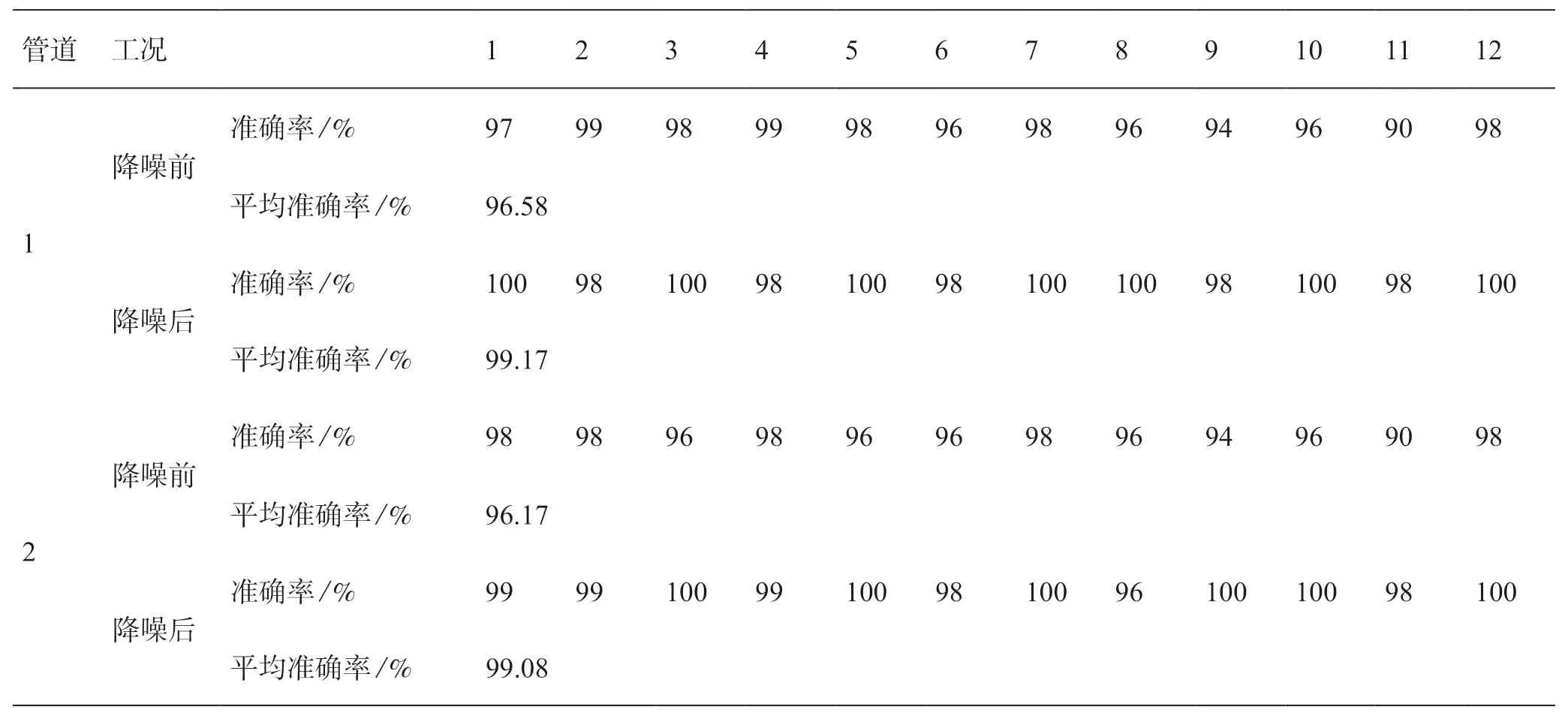
表2 基于T-SNE的各工况识别准确率Table 2 Identification accuracy of each condition based on T-SNE

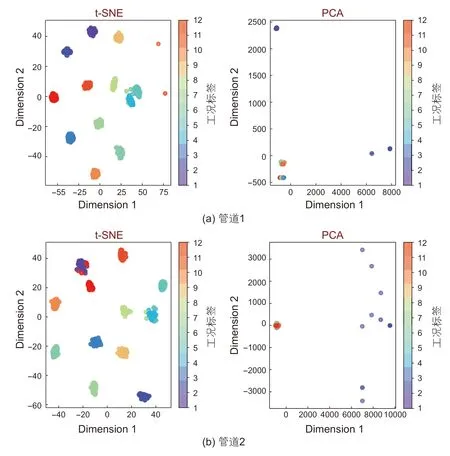
图5 T-SNE与PCA降维聚类结果对比Fig. 5 Clustering result comparison of T-SNE and PCA dimension-reducing

为对比说明T-SNE聚类识别的优越性，选用传统机器学习非线性分类算法如人工神经网络(ANN)、决策树(DT)以及随机森林(RF)进行分类比较。依据机器学习算法中数据集划分的经验总结(训练集占80%，测试集占20%)[30]，对管道数据集进行划分，以识别准确率作为模型评价指标。为避免传统机器学习模型的波动性对实验结果造成影响，对每个模型进行10 次实验，得出各模型的平均准确率。通过多次测试确定各个模型的参数，表3、4 和5 是各对比模型的参数设置情况，表6 是每个模型运行所需时间。

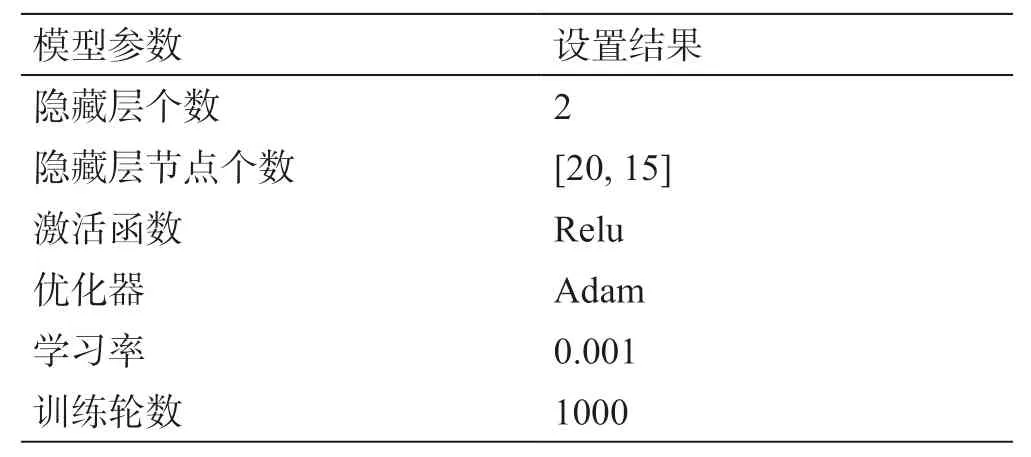
表3 ANN模型参数设置结果Table 3 The parameter setting results of ANN model

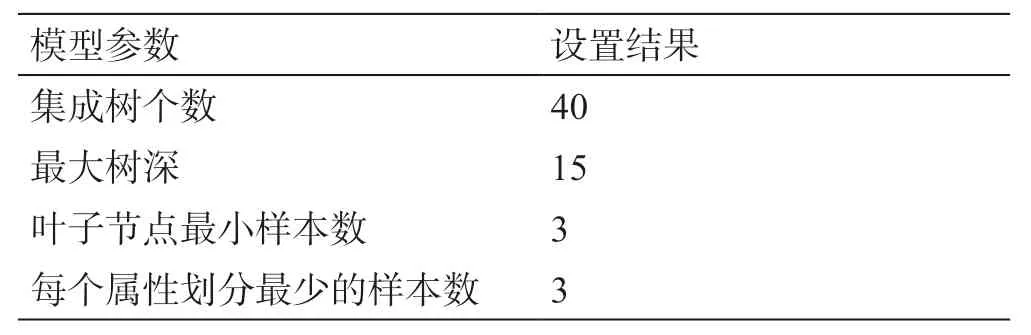
表4 RF模型参数设置结果Table 4 The parameter setting results of RF model

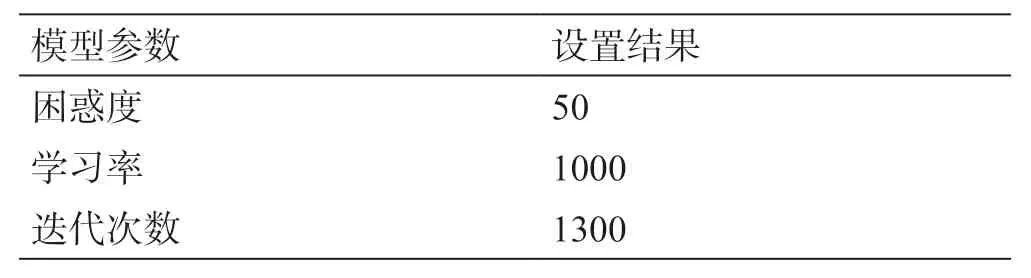
表5 TSNE模型参数设置结果Table 5 The parameter setting results of TSNE model

表6 识别模型运行时间Table 6 Running time of identification model

图6 和图7 分别为不同识别模型在训练集和测试集的识别准确率，可看出对于管道1，降噪前DT的识别准确率最高，达到96.91%，T-SNE的识别准确率为96.58%，但对于降噪后的数据，T-SNE的识别准确率达到99.17%。而对于管道2，降噪前RF的识别准确率最高，达到96.19%，T-SNE的识别准确率为96.17%，但降噪后，T-SNE的识别准确率可达到99.08%。基于模型结果，可说明CAE-TSNE对管道多种运行工况的识别准确度最高，表现最好。

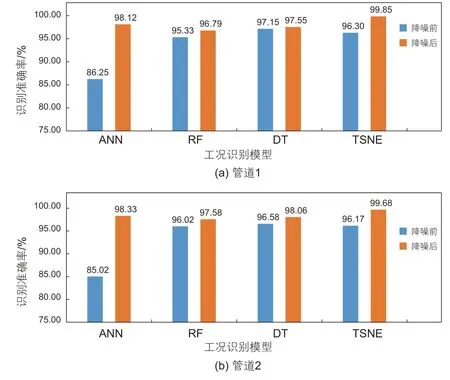
图6 不同分类模型在训练集上的准确率对比Fig. 6 Comparison of the accuracy of different classification models on training sets

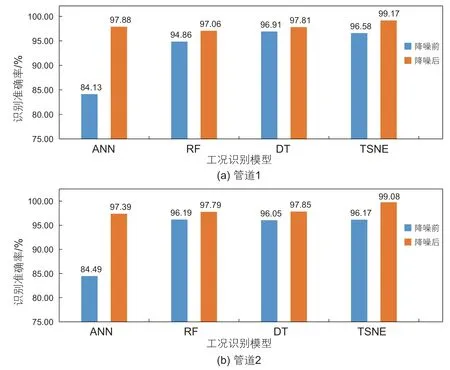
图7 不同分类模型在测试集上的准确率对比Fig. 7 Comparison of the accuracy of different classification models on testing sets

3 结论

本文针对成品油管道运行工况识别开展研究，旨在帮助现场更好地监控管道运行状态。首先根据管道SCADA系统获取运行数据，考虑到管道运行数据具有时间序列以及物理空间特性，将一段时间的运行数据构造为二维矩阵。基于CAE算法对矩阵数据进行降噪，得到滤除噪声后的运行数据；基于T-SNE聚类算法对降噪后的运行数据进行工况的聚类识别，建立管道运行工况识别模型。为验证模型的准确性和通用性，选取两条管道的12 种运行工况数据，并对比ANN、DT以及RF的识别效果。结果表明，基于CAE-TSNE的工况识别模型对降噪后的运行数据识别准确率可达到99%以上，表现效果最好，可用于指导成品油管道运行状态的识别和监测。