高阻地层HDIL 阵列感应影响因素分析与校正方法

王嵩然，李潮流*，刘英明，王磊，胡法龙

1 中国石油勘探开发研究院，北京 100083

2 中国石油大学(华东)地球科学与技术学院，青岛 266580

0 引言

四川盆地川中蓬莱区块是近几年天然气勘探开发的重点，主要目的层灯影组碳酸盐岩储层常规测井响应特征可简单概述为低自然伽马、中高电阻率，具有工业产能的气层段电阻率一般在200～2000 Ω·m，属于高阻地层。钻井过程中，为维护井筒质量、提高钻速避免卡钻等工程事故，常采用油基钻井液，使得裸眼井必须采用阵列感应测井。感应测井采集的是地层电导率信号，在目的层普遍为高阻的背景下，仪器测量的电导率信号幅度和信噪比低，多口井资料显示仪器采集的原始电导率信号存在大段负值、软件聚焦后的阵列电阻率曲线平直无规律，不反映地层岩石物理特征，无法用于含气性解释和储层评价。因此，考察包括井筒和地层岩石在内的不同因素对阵列感应测井原始电导率信号的影响规律，对于分析此类复杂背景下导致测井响应异常的原因至关重要，相关认识和结论可以为仪器改进和新的信号合成处理方法研究提供参考。

前人围绕阵列感应测井已开展很多研究，主要成果可分为正演和反演两大类。正演是已知仪器和地层参数求测井响应的过程，而反演是已知仪器参数和测量曲线反求地层参数[1]。

在阵列感应测井正演算法研究方面，江国明等将理论计算方法分为解析法和数值模拟计算两大类，并对比分析了不同计算方法的优势[2]；仵杰正演分析泥浆侵入模型下感应测井的响应，讨论了饱和度、矿化度等因素导致油层阵列感应测井负差异的形成机理[3]；范宜仁对大斜度井的感应测井进行了特征分析[4]；谭茂金提出了新的针对非均质地层感应测井响应的计算方法[5]；邓少贵等计算了基于层状各向异性介质多分量感应测井响应解析解并快速提取水平电阻率[6]；李潮流提出了一种针对倾斜电各向异性地层阵列感应测井数据处理新方法[7]；汪宏年等应用模式匹配等算法建立了多分量阵列感应测井响应的快速算法[8]。

在反演方面，李虎等从几何因子理论出发，提出了阵列感应测井的五参数最小二乘反演[9]；汪功礼、邓小波等利用三维有限差分反演感应测井电阻率和介电常数[10-11]；Yang C、Finol J等分别采用离散牛顿法、模糊识别等方法反演侵入带电阻率、原状地层电阻率和侵入深度等参数[12-13]。杨伟、汪宏年等提出了快速计算雅可比矩阵、提高电法测井反演速度的方法[14-15]；姜艳娇等分析了钻井液侵入对阵列感应测井响应的影响[16]; 仵杰等讨论了饱和度、矿化度等因素导致油层阵列感应测井负差异的形成机理，其认识对于提高复杂地层条件下储层参数的反演精度很有价值[17]。这些技术成果为提高复杂储层测井解释符合率和储层参数计算精度提供了重要手段。

综上所述，围绕阵列感应测井正反演方法研究，前人多侧重于在低电阻率背景下对比分析不同算法的优势，并总结出在不同井筒和地质背景下的响应特征与主要影响因素。而在油基钻井液背景下，高阻碳酸盐岩地层中阵列感应测井的响应特征分析是近些年来出现的新需求，在这一领域前人并未有过详细研究。本文以HDIL阵列感应仪器为例，借鉴前人的成果采用正演模拟算法，分析井径、侵入深度以及钻井液-地层电阻率对比度等因素对测量信号的影响规律，并提出了一种基于Archie理论的原始电导率信号约束校正方法。

1 模拟方法简介

1.1 HDIL仪器简介

高分辨率阵列感应(High Definition Array Induction Log，以下简称HDIL)是目前国内应用较为广泛的感应类测井仪器，包含一个发射线圈T、7 个主接收线圈R和7 个屏蔽线圈[18]，每一组对应序号的接收线圈和屏蔽线圈绕向相反，并与接收线圈串联组成一个子阵列。因此，该仪器共包含7 个子阵列，每个子阵列都采用8 种工作频率同时工作，采集实部和虚部两种信号，一共测量112 个信号[19]，经过数据处理得到3 种分辨率(1 ft、2 ft和4 ft)6 种探测深度(10 in、20 in、30 in、60 in、90 in和120 in)共18 条测井曲线[20-21]。

1.2 感应信号的计算

感应测井是利用电磁感应原理；以双线圈为例，发射线圈中的交变电流通过地层单元环在接收线圈中产生二次感应电动势，其信号强度与地层电导率有关[22]，理论计算公式为：

其中，σa为电导率测量信号，S/m；VR为仪器测得的电动势实部信号，V；K为仪器常数，其大小与仪器结构有关。

HDIL仪器的7 个子阵列的测量信号可以近似看成是双线圈系测量信号的叠加，叠加的理论响应公式如下[22-23]：

式中，σa总为叠加后的视电导率，S/m；nTj为Tj的匝数；nRk为Rk(第k个接收线圈)的匝数；Ljk为Tj和Rk之间的距离，m；σajk为线圈对Tj和Rk所测的视电导率，S/m。l为发射线圈的个数；m为接收线圈的个数。

该公式表达了多线圈系子阵列的信号合成与所包含的双线系及线圈之间的距离以及线圈匝数的关系。采用有限元算法，将仪器响应范围内的求解域分割为数量有限的四面体、六面体单元，继而采用一些较为简单的插值函数对各个单元进行求解。通过数值计算，可以得出仪器响应范围内感应信号的数值解，再结合公式(2)进行叠加运算，就可以计算各子阵列的视电导率σa。

利用上述方法，结合研究区碳酸盐岩储层的实际特征，假设地层为无限厚，不考虑围岩影响，设计如图1 所示的模型。图1 中，Lh、Li分别为井径和侵入半径，cm；Rm、Ri和Rt分别为钻井液、侵入带和原状地层的电阻率，Ω·m。通过逐一改变相关参数(如：钻井液电阻率，侵入半径等)并控制其他因素不变，模拟计算各子阵列的电导率信号，可以分析该因素变化对不同子阵列的响应规律(本文不讨论分辨率问题，以下展示的各子阵列的模拟数值均为趋肤校正后的结果)。

图1 模拟HDIL仪器测量信号的无限厚有侵入地层模型Fig. 1 The infinite thick invasive strata model for simulating HDIL instrument measurement signals

2 HDIL 影响因素模拟分析

2.1 对比度的影响分析

2.1.1 不同岩性地层与钻井液类型的对比分析

为便于讨论，本文定义原状地层与钻井液电阻率比值为对比度，记为COR，公式为：

蓬莱地区灯影组碳酸盐岩地层采用油基钻井液，本文以该地区实际测井资料为依据，建立不同模型，讨论对比度影响的模型参数如表1 所示。

表1 探究对比度影响的模型参数Table 1 Exploring the model parameters influenced by contrast

根据表1，设计的模型1、2 分别模拟碳酸盐岩地层油基和水基钻井液的HDIL仪器各子阵列响应；模型3、4 则分别模拟砂泥岩地层油基和水基钻井液情况。模拟结果如图2 所示。图2a是7 个子阵列在4 个模型中的电阻率模拟结果，横坐标为各子阵列的编号，图中虚线为两组模型的地层真电阻率。图2b是HDIL仪器最短、最长源距和中间源距3 个子阵列测量相对误差与对比度的相关性分析图版，横坐标为4 个模型的对比度。

图2 碳酸盐岩与砂泥岩不同钻井液条件阵列感应模拟Fig. 2 Array induction simulation of different drilling fluid conditions for carbonate rock and sandstone (a) resistivity simulation of different model sub arrays; (b) relative resistivity error of different model sub arrays

从图2a可以看出，在4 种模型中，无论地层背景电阻率高低，随着子阵列源距的增加，长源距子阵列的测量值更接近模型的真电阻率，测量误差更小(图2b)。根据几何因子理论，长源距子阵列探测深度大，受井眼影响小，因此在各种模型条件下其测量结果更接近真实值。例如，最长源距的子阵列7 在4 种模型中其测量误差均小于10%。另一方面，对比度是影响各子阵列测量误差的关键。图2b中当模型的对比度接近1 时相对误差最小，对比度越偏离1，各子阵列的测量误差也越大。

2.1.2 油基钻井液下不同地层电阻率分析

仍然采用图1 所示的模型，井径和侵入半径与表1 中的参数一样，在油基钻井液条件下，根据研究区目的层电阻率变化特征，设置Rt变化范围248～3630 Ω·m，侵入带电阻率Ri变化范围265～3701 Ω·m(数据来自实际井资料，非等间距变化，具体数值参见表2)。经过数值模拟，不同子阵列经趋肤校正后的视电导率曲线MSECi如图3 所示。

表2 模拟改变原状地层/侵入带电阻率时HDIL仪器响应的参数表Table 2 Parameter table of HDIL instrument response when simulating changes in the original formation/intrusion electrical resistivity

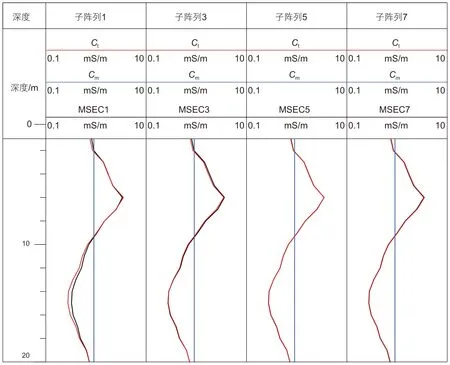
图3 油基钻井液改变碳酸盐岩电阻率HDIL子阵列响应变化模拟结果Fig. 3 Simulation results of changes in HDIL sub array response to changes in carbonate rock resistivity caused by oil-based drilling fluid

为便于观察和分析模拟结果，图3 采用类似测井曲线的方式绘图，但需要指出的是，图3 中的深度没有实际意义，每一个深度采样点对应的是一个模型，在假设地层无限厚的情况下模拟子阵列的电导率。

在油基钻井液条件下，碳酸盐岩地层电阻率Rt由200 Ω·m变化到3000 Ω·m，对应COR为0.225～3.3，接近于1，图3 中各个子阵列经趋肤校正后的视电导率MSECi与地层真电导率Ct基本重合。

进一步结合图2 中的模型1 和模型2 模拟结果对比分析，无论是改变钻井液电阻率Rm，还是改变地层背景值Rt，HDIL仪器子阵列的响应都是受对比度COR控制。COR接近于1，更多的子阵列，甚至包括最短源距子阵列1，其理论结果都可能与地层真实值Ct接近。

2.2 侵入深度的影响

尽管目前关于油基钻井液在高温高压井眼环境中破乳变性的研究还没有明确结论，实际钻探资料揭示采用油基钻井液时可能存在油性基液侵入地层的情况[26]，假设侵入的基液与钻井液具有相同的电阻率，采用与图1 所示的模型，设置侵入半径分别为10、50 和100 cm，作为对比研究，分为低侵和高侵两组地层模型，具体参数见表3，模拟结果如图4所示。

表3 探究侵入深度影响模型参数表Table 3 Exploring the impact of intrusion depth on model parameters

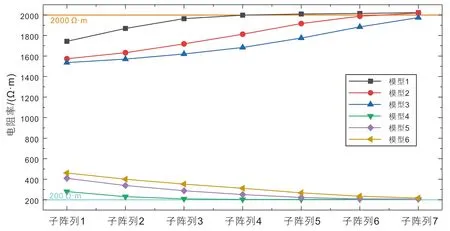
图4 碳酸盐岩地层油基钻井液不同侵入深度的HDIL子阵列误差分析Fig. 4 Error analysis of HDIL subarray for oil-based drilling fluids with different invasion depths in carbonate formations

图4 表明，无论是低侵还是高侵，对于同一个子阵列，侵入较浅的(模型1 和模型4)测量误差较小，侵入越深(模型3、模型6)所有子阵列的测量误差都被放大。由此可见，侵入程度越浅，各子阵列的测量误差越小，所以在现场施工时应该强调及时测井。

另一方面，在相同的侵入深度下，原状地层背景电阻率Rt越大，各子阵列的测量误差就越大(例如图4中的模型1 与模型4 相比，其它依此类推)。而且短源距子阵列的测量误差比长源距子阵列的更大；从径向几何因子的角度来说，源距越短的子阵列其径向响应更多地来自井筒附近的贡献，探测距离更浅，受到钻井液的影响也就更大；源距越长，来自原状地层的贡献越大，因此不同探测深度曲线出现分离，表现为侵入特征。所以在使用油基钻井液时，对于具有高电阻率背景的致密碳酸盐岩地层，短源距子阵列的误差非常显著，在软件聚焦信号合成时应更多的考虑长源距子阵列的贡献，在可能的情况下应摒弃短源距子阵列的信号，研究新的聚焦处理算法。

除此之外，井眼的扩径程度对阵列感应测井响应也会产生影响，扩径越严重、各子阵列接收的响应中油基钻井液的贡献就越大，就越难以探测到地层真实信号[24]，而且短源距子阵列比长源距子阵列受到的影响更大，限于篇幅，本文不再详细讨论。

3 实际资料响应特征分析

为了验证上述基于数值模拟结果的分析结论是否正确，下面结合实际井的测井资料响应特征来进一步讨论。

图5 所示为研究区A井目的层段HDIL响应特征分析实例。本井在钻井过程中采用油基钻井液，钻穿目的层之后用水基钻井液替换并完成了双侧向及阵列侧向测井。图中的Ct曲线是基于阵列侧向测井RLA5计算的电导率曲线，COR曲线是假设Rm=1100 Ω·m，结合Ct根据式(3)计算的对比度，MSEC1、MSEC3、MSEC5 和MSEC7 分别是子阵列1、3、5 和子阵列7经过趋肤校正后的电导率曲线，为了显示负值异常采用线性刻度。

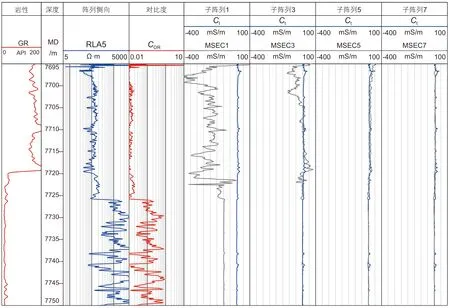
图5 A井目的层子阵列电导率曲线分析Fig. 5 Analysis of the conductivity curve of the target layer sub array in Well A

从图5 可以看出，图中上部对应A井7695～7725 m井段阵列侧向测井揭示地层电阻率较低，一般在200 Ω·m以下，COR平均值约为0.01，Rm显著高于Rt，再加上高温对电子线路的温漂影响，导致子阵列1 的电导率信号在该井段出现负值异常，子阵列3 仅在局部出现负值异常，而对于长源距子阵列(子阵列5 和子阵列7)的电导率数据基本正常，与Ct曲线重叠程度高。

图5 中的7725～7750 m井段阵列侧向测井揭示地层电阻率在1000 Ω·m左右，与钻井液电阻率接近，COR数值在1 左右。根据前面的理论分析长源距子阵列一般能够获得接近地层真实值的原始信号，可以看出，子阵列5 和7 的电导率与地层真实值Ct基本重合，而子阵列1 的电导率仍然为负值异常。

整体上看，图5 中自上而下地层真电阻率增大、电导率降低，COR数值趋近于1，所有子阵列的电导率自上而下都是逐渐接近地层真实电导率，测量绝对误差逐渐降低，而子阵列1 的测量信号基本上都是异常，不能用于后续处理。

图5 中短源距子阵列信号更易失真，主要原因是高温深井中短源距子阵列受温度变化影响更明显，而目前的温度校正过程尚不完善，同时短源距子阵列受高阻油基钻井液的极低电导率影响更大。作为对比，长源距子阵列的信号相对更稳定，图5 中最后两道子阵列5 和7 的测量电导率曲线与地层真电导率曲线Ct基本重合，个别点异常可认为是传感器本身测量误差所致，温度的影响相对较小。

A井的实际响应特征说明，HDIL仪器的各个子阵列源距越长，测量信号的贡献更多的来自原状地层本身，测量误差越小，具体误差取决于COR值。对于油基钻井液而言，碳酸盐岩地层电阻率越高，各个子阵列的测量误差越小，但短源距子阵列受钻井液的高阻及其它因素的多重影响，出现负值异常。这些规律验证了前面数值模拟结果的可靠性。

4 弱信号的约束校正

综上所述，在油基钻井液钻井液碳酸盐岩地层中，HDIL仪器的多个子阵列出现负值异常，不能直接应用于后续处理。考虑到国内大量采用与仪器捆绑的商业软件进行资料处理、缺乏第三方可定制可编辑的独立软件的现状(如Express软件是目前处理HDIL仪器数据的主流软件)，我们几乎无法改变软件流程中的任何模块，因此本文提出一种基于Archie理论对趋肤校正后的电导率信号进行约束校正，然后再应用商业软件进行软件聚焦处理的新思路。

Archie公式建立了储层电阻率与孔隙度及其孔隙结构之间的桥梁，是计算饱和度的基础。反之，如果假设储层完全饱含气(含水饱和度等于束缚水饱和度)，在已知孔隙度、岩电参数及地层水电阻率的情况下，则可以利用该公式估算储层的理论电阻率上限[25]。

目标层位泥质含量一般低于10%，可以忽略其对电阻率的影响，根据实验结果，m=2.13，n=2.04，a=0.97，b=1.11，换算到地层条件下的Rw=0.016 Ω·m。假设储层饱含天然气，对应束缚水饱和度Swir=30%，在准确计算储层孔隙度的前提下利用Archie公式估算其电导率下限σmin。

分析HDIL仪器测量数据的各处理流程，发现尽管原始信号存在负值异常，商业软件的井眼校正过程对上述异常值采取了强制赋值限制(在井眼校正步骤中令所有子阵列的电导率不小于0.5 mS/m，对应电阻率2000 Ω·m，研究区高于2000 Ω·m的地层均为非储层)，本文依据上面计算的电导率下限对经过趋肤校正后的曲线做初步的异常约束校正，即强制各子阵列的趋肤校正后的结果不低于上述电导率下限Cmin，然后再开展软件聚焦处理，可以显著改善最终输出的阵列电阻率曲线质量。

图6 为研究区B井电导率信号约束校正应用实例，图中第4 道MSEC1～7 曲线为HDIL仪器7 个子阵列趋肤校正结果，第5 道是经过上述约束校正后的结果，第6、7 道分别为4、5 道数据经过软件处理后的最终输出结果。

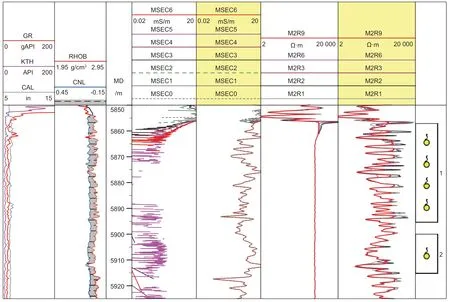
图6 B井气层段HDIL仪器各子阵列电导率信号下限值约束校正前后结果对比Fig. 6 Comparison of results before and after constrained correction of the lower limit values of conductivity signals in each sub array of HDIL instrument in the B well gas reservoir section

图6 中展示了本井1～2#储层段采用约束校正算法的效果对比。整体上，在1～2#储层段表现为高阻特征，原始数据经趋肤校正后大部分失真(第4 道)，经过软件聚焦处理后输出的不同探测深度曲线都重叠并且整体平直(第6 道)，不能反映储层的真实特征。与此对比的是，利用电阻率下限约束校正后的曲线(第5道)质量得到提升，再利用软件聚焦处理后的输出结果(第7 道)的曲线变化反映了储层物性的变化，在上部储层段均表现为低侵，指示储层可能含气。测试结果证实，1～2#储层段日产天然气超过120 万m3，无水。

图7 为研究区C井水层段的处理结果，各道曲线同图6。与图6 相比，C井5～7#储层段背景电阻率明显降低，但第4 道中仍有部分短源距子阵列趋肤校正后的曲线存在异常(图中6295 m以下井段)，软件聚焦处理后的不同探测深度曲线(第6 道)出现了镜像特征，即在物性发育的储层段浅探测电阻率与深探测电阻率曲线变化趋势相反，完全不符合岩石物理规律。经过上述约束校正后处理后的结果很好地避免了这种异常(第7 道)，不同探测深度的电阻率曲线呈现典型的高侵水层特征，也得到了测试证实。

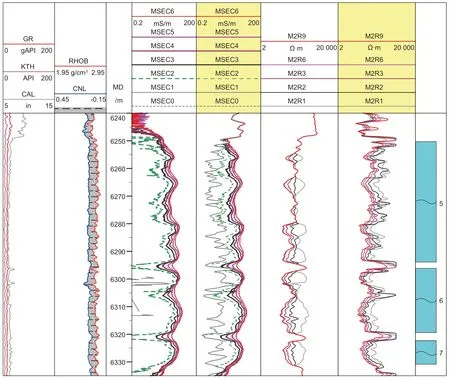
图7 C井水层段HDIL仪器各子阵列电导率信号下限值约束校正前后结果对比Fig. 7 Comparison of results before and after constrained correction of the lower limit values of conductivity signals in each sub array of HDIL instrument in the C well water interval

图8 为研究区深层钻探井D井HDIL测井资料分析实例。本井完钻井深超过9000 m，创亚洲垂直井深度记录，测井时井底温度接近200 ℃，仪器温漂现象特别明显，图8 中第3 道为原始的7 个子阵列趋肤校正后的电导率曲线，仅长源距子阵列6、7 的曲线基本正常，其余多个线圈的信号均出现负值异常，软件聚焦处理后的不同探测深度电阻率曲线(图8 第5 道)完全重叠，而且最低探测深度曲线M2R1 与其它曲线严重偏离，说明多个原始线圈的信号受油基钻井液及高温的影响，处理结果已严重失真。利用上述方法进行约束校正后处理结果(图8 第4 道和第6 道)与第1 道自然伽马曲线反映的岩性变化基本一致，不同探测深度的电阻率曲线也与第1 道的孔隙度曲线一致地反映了储层物性的变化，进一步验证了本文方法的适用性。

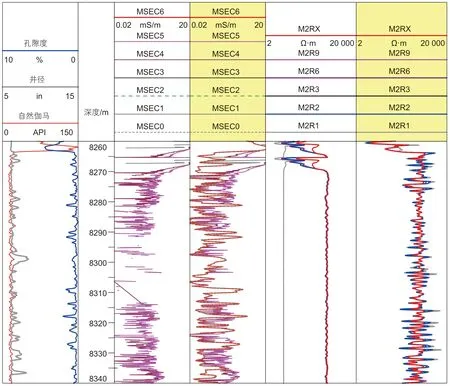
图8 D井HDIL仪器各子阵列电导率信号下限值约束校正前后结果对比Fig. 8 Comparison of results before and after constrained correction of the lower limit values of conductivity signals in each sub array of the D well HDIL instrument

5 结论与认识

(1)钻井液与地层岩石的电阻率对比度是控制阵列感应仪器各子阵列响应的重要因素，深层高温也是另一个重要因素。对比度越接近1，各子阵列响应越接近地层真实值。在碳酸盐岩地层中使用油基钻井液时，由于物性及含气性变化严重影响地层背景电阻率，导致对比度变化大，在有效储层段地层电阻率降低使得对比度减小，使得测量误差变大，短源距子阵列严重失真。

(2)模拟结果表明，除对比度以外，钻井液的侵入深度是影响各子阵列测量误差的另一个重要因素。在碳酸盐岩地层使用油基钻井液时，长源距子阵列的测量信号受井径变化及侵入程度的影响小，在后期的信号合成过程中应该多考虑长源距的信号，以提高合成曲线的精度。

(3)在油基钻井液碳酸盐岩地层的地质背景下，叠加高温等环境因素的影响，阵列感应仪器记录的原始信号存在大量负值异常。基于Archie公式的电导率约束校正更客观地消除了原始信号的负值异常，为后续处理提供了相对更准确的数据。