基于聚类及长短时记忆神经网络预测油田产量

王洪亮，林霞，蒋丽维，刘宗尚

中国石油勘探开发研究院，北京 100083

0 引言

准确预测油田产量是解决油田生产优化、提质增效等问题的基础。近年来，人工智能在油气行业得到广泛应用[1-6]。许多学者利用人工智能技术基于油田开发动态数据进行油气产量预测[7-12]。机器学习技术作为油田产量智能预测常用的人工智能方法，建立产量预测模型需要大量训练样本数据[13-16]。构建产量预测模型可以利用油田生产数据或者油井生产数据。利用油田生产数据建立预测模型，将油田当成一个整体，由于训练样本少，泛化能力弱；利用油井生产数据建立模型，训练样本多，但由于单井产量波动大，每口井递减规律差异明显，样本标注难度大，且数据处理工作费时耗力。因此，需要开发一种既准确又高效的油田产量智能预测方法。

在油气产量智能预测方面，一些学者已经分别在油田产量预测和油井产量预测方面开展了研究工作[12,17-20]。在油田产量智能预测方面，吴新根[21]在1994 年利用人工神经网络预测了前苏联罗马什金油田的原油年产量，通过与Weng旋回模型预测结果比较，证明了利用人工神经网络预测石油产量的可行性。王洪亮[22]提出了基于循环神经网络的油田特高含水阶段产量预测方法，综合考虑不同年份的投产井数、产量构成数据、注水井数、月注入量、含水率、生产天数、剩余可采储量、措施井次和措施增油量等产量影响因素，拓展训练样本考虑因素的广度以增加预测模型的泛化能力。张瑞[23]在井网分析的基础上通过多变量时间序列分析对注采井组数据进行优选，并将井组内不同采出井产油量及注入井注水量作为彼此相关的时间序列，通过建立向量自回归模型从多个时间序列中提取出相互作用规律，挖掘注采井间流量的依赖关系从而进行产量预测。黄家宸[24]等介绍了机器学习技术在油田静态产量和动态产量预测的应用方法并进行实例验证，认为由于不同油田之间存在差异，模型复用难度大。油田产量预测的主要方法为基于该油田的产量、井数和压力等动态数据，利用机器学习算法建立预测模型，预测未来。主要优点为油田生产趋势平稳，数据量少，易于整理和加工，建模工作量小。缺点为机器学习算法需要大量样本数据进行模型训练，而以油田作为研究对象，样本数据少，容易发生过拟合，模型迁移难度大。

在油井产量智能预测方面，通过分析人工神经网络在油气工业的应用，总结出油田开发领域应用人工神经网络的方法论。主要包括特征选择及数据采集、数据集划分、数据标准化和模型训练4 个步骤。谷建伟[25]基于产油量变化的时间序列数据特征，提出利用长短时记忆循环神经网络模型实现具有长时间记忆能力的油井生产时间序列预测。通过对结果进行分析，认为该方法可以较好的预测油井产量变化，部分油井预测不准确的原因为产油量突然大幅度增加、无预兆停产、大型作业措施和数据缺失等。油井产量预测的主要方法为基于油井的有效厚度、渗透率、产量和压力等动静态数据，建立预测模型。主要优点为训练样本丰富多样，模型鲁棒性高，通用性强。缺点为单井产量波动大，每口井递减规律差异明显，逐口井分阶段样本标注困难，数据处理工作耗时。

可以看出，前人为了建立油田或者油井产量智能预测模型，分别利用不同方法构建了油田或者油井产量智能预测所需的训练样本数据，在此基础上应用机器学习算法进行模型建立。油田样本数量少，容易发生过拟合，迁移难度大。油井样本数量多，模型鲁棒性高，但数据处理工作量大。本文首次将油田和油井生产数据有机融合作为训练样本，建立产量智能预测模型，预测油田产量。首先采用无监督学习的K均值聚类算法依据有效厚度、孔隙度、渗透率、饱和度等信息对油井进行聚类，识别油田中不同油井的产量递减规律，并将每类油井转换成一口典型油井作为该类油井的代表；其次，将典型井作为预测对象，通过从每类油井中按比例随机抽取油井来增加训练样本数量，即将典型井和油井生产数据进行融合构建训练样本；最后，基于循环神经网络能够实现产量与压差、储层特征等影响因素之间的复杂映射，同时兼顾产量随时间变化的趋势和前后关联的优势，利用堆叠去噪自编码+长短时记忆循环神经网络建立模型预测典型井产量，进而预测油田产量。

1 原理与方法

1.1 聚类

聚类是指将物理或抽象对象的集合分组为由类似的对象组成的多个类的分析过程。每类称为一个簇，同一个簇中的对象彼此相似，不同簇中的对象彼此相异。

从油层物理角度看，聚类的同一类别内生产井的储层物性和生产规律差异较小，不同聚类类别间生产井的储层物性和生产规律差异较大。给定m×n的样本X={x1,x2,...,xn}，则样本之间的距离dij为

式中，xki和xkj分别为第i个样本和第j个样本的第k个特征。

定义样本到分类中心距离的和为最终损失函数，即

1.2 数据转换方法

将多口油井转换成一口具有代表性的典型油井。典型油井的日产油、日产液等动态指标等于多口油井的算数平均值，有效厚度、孔隙度、渗透率、压力等静态指标等于多口油井按单井控制储量的加权平均值。

1.3 样本标注方法

利用人工智能方法预测油井产量，影响因素作为预测模型的输入，产量作为预测模型的输出，属于监督学习。监督学习算法需要“教材”供机器学习，即训练样本。油井生产训练样本是指油藏类型、地质条件、开发技术等影响因素与油井产量之间的对应关系。机器学习算法基于训练样本学习产量与影响因素之间的复杂映射关系，建立具有泛化能力的预测模型。

首先对油井生产阶段进行标注，去除长期关井、修井、生产异常、数据缺失等非正常生产阶段；其次综合考虑开发层系、开发阶段、含水阶段、产量递减率和含水上升率等指标，分别制定区块/油井分组、油井生产阶段和训练样本优选的规则，测算指标范围，制定油井训练样本选择标准。最后依据选择标准，标注油井生产训练样本。

1.4 长短时记忆循环神经网络

与普通回归任务不同，时间序列预测在时间上具有复杂的前后依赖关系。循环神经网络的结构可以让之前时间步中的有用信息持续保留并参与后续时间步的运算。然而，如果先前的相关信息所在的位置与当前时间的距离非常远，由于不断输入数据的影响，模型中的记忆单元(单一的tanh层或sigmoid层)无法长期有效地保存全部历史信息，容易产生梯度消失或者梯度爆炸等问题。

针对传统的循环神经网络存在的问题，Hochreiter等人针对网络结构进行改进，提出了长短期记忆神经网络(Long Short-Term Memory，简称LSTM)。

该模型是一种在循环网络中具有4 个相互作用层的循环神经网络，它改进了传统网格模型中的记忆模块。通过增加门结构和记忆单元状态，使得LSTM可以让时间序列中的关键信息进行有效的更新和传递，有效的将长距离信息保存在隐藏层中。由于信息可以在循环神经网络中自由流动，基于该方法预测油田产量综合考虑了产量随时间变化的连贯性，更加符合实际生产情况。

LSTM中的隐藏层的循环网络包含遗忘门、输入门、输出门和1 个tanh层，如图1 所示。

第1 个交互层被称为遗忘门层，它决定当前步骤遗忘的信息。遗忘门的计算方法可表示为：

第2 个交互层被称为输入门层，它决定了哪些新的信息应该添加到处理器状态中。输入门层的sigmoid函数决定了要更新的数值，计算方法可表示为：

第3 个交互层被称为tanh层，它创建了一个可以添加到处理器状态中的新候选值，增加到神经元状态中。这一层计算得到的值经过tanh函数运算，使结果趋于平稳状态。计算方法可表示为：

在上述3 层计算之后，携带信息的处理器状态Ct-1与包含新信息的候选值结合求和，计算方法可表示为：

最后一层是输出门层，它基于更新后的处理器状态生成LSTM的输出值，是建立在神经元状态基础上更新的版本。

首先，sigmoid层决定哪一部分的神经元状态需要被输出，然后神经元状态经过tanh层并与sigmoid门的输出相乘得到输出结果。计算方法可表示为：

处理器状态有选择的保存先前时间步骤中的有用信息并贯穿整个LSTM。交互层中的门结构可以根据上一时间步的隐藏状态和当前时间步骤的输入信息对处理器状态中的信息进行增加、删除和更新操作，更新后的处理器状态和隐藏状态向后传递。

2 方法流程

方法流程主要包含油田开发现状分析、油井聚类分析、训练样本标注和产量预测模型构建4 个步骤，如图2 所示。

图2 机器学习模型技术路线图Fig. 2 Machine learning model technology roadmap

油田开发现状分析。分析油田的储层、流体和开发历程等基础信息，重点分析油田的产量变化情况，确定产量递减的范围。

油井聚类分析。利用霍普金斯统计量进行油井聚类趋势评估，利用“肘方法”确定聚类，利用K均值聚类算法对油井进行聚类分组。依据聚类分析结果，将每类油井转换成一口油井作为该类油井生产规律的代表。

训练样本标注。提出油井生产数据训练样本标注方法与流程。依据油田开发现状分析结果，删除因套损、水淹等导致的长期关井及生产数据缺失等生产异常阶段，将油井正常生产阶段的生产状态和与之对应的产量标注为一个训练样本。从每类油井中按比例抽取一部分油井，将典型井和抽取的油井共同作为样本进行训练样本标注，建立样本集合。

产量预测模型构建。利用皮尔森相关分析方法分析油井产量的主控因素，确定模型的输入特征；将数据集划分为训练集和测试集，训练集用于模型训练，测试集用于结果验证；利用长短时记忆循环神经网络建立产量预测模型。

3 实例应用

3.1 油田开发现状分析

以国内某背斜构造中高渗砂岩油藏作为研究对象。该油田共发育三套油层，地层厚度约500 m。具有统一的压力系统和油水界面，底水、边水不活跃。原油粘度从8.3 至9.2 mPa·s，地饱压差较小。

该油田采用早期注水开发，注采比大于1.1，地层压力保持水平高。自1963 年投入开发以来，该油田经过多次加密。目前共有生产井近700 口，其中采油井370 口。目前，油田年产油量近30 万t，综合含水95.3%。油田分为两套开发层系进行开采，A油层日产油530 t，自然递减率为4.4%左右，单井日产油2.6 t；B油层日产油290 t，自然递减率为3.1%左右，单井日产油1.9 t，两套开发层系产量规模与递减规律不同，如图3 所示。

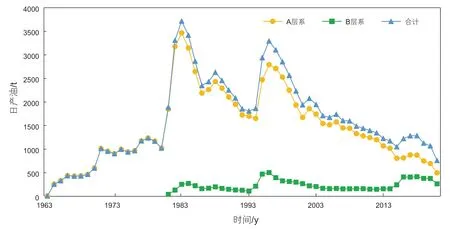
图3 日产油生产运行曲线Fig. 3 Daily oil production running curve

由于不同投产批次油井生产时间不同，目前单井日产油最大值为12.5 t，最小值为0.3 t，平均值为2.3 t，方差为2.1；油井含水率最大值为96.5%，最小值为78.2%，方差为6.8%。不同投产批次油井之间产油能力差别较大。措施增油方式以调参、换泵、补孔和压裂为主，其产量占总产量的7%左右。

综上所述，该油田具有开发层系多、生产历史长、油井投产批次多、处于特高含水后期等特点，将油田作为一个整体进行产量预测无法体现不同投产批次油井的各自的生产特点；利用常规油藏工程方法依据储层特性、投产批次、含水阶段等特征对油井分组，并按分组进行产量预测难度大，且工作量大。本文拟利用基于聚类及长短时记忆神经网络的油田产量预测方法，提高预测精度和工作效率。

3.2 油井聚类分析

3.2.1 聚类趋势评估

霍普金斯统计用于通过测量给定数据集由统一数据分布生成的概率来评估数据集的聚类趋势。如果数据集聚类趋势不明显，则霍普金斯统计量的值接近0.5；如果数据集有明显的聚类趋势，则其值接近1。计算370 口油井生产数据的霍普金斯统计量为0.88，说明数据集有明显的聚类趋势。

3.2.2 确定聚类数目K值

利用“肘方法”[26]确定聚类的K值，即计算数据集中所有样本点到聚类中心的簇内误差平方和(within-cluster sum of squared errors , SSE)，根据SSE随K的变化选取K值。

图4 为“肘方法”确定K值的示意图。随着K值的增加，SSE逐渐减小，当K值等于3 时，SSE 减小变化缓慢，如图4 所示，红色圆圈内的值为K值。因此K-Means 将把数据集分为3 个聚类类别。

图4 “肘方法”确定聚类的K值Fig. 4 Diagram of elbow method determining value of K

3.2.3 聚类结果

按照有效厚度、渗透率、井距、日产油、累产油、采出程度、静压和流压进行油井聚类分析，聚类分析结果图，表现出良好的聚类特性，如图5 所示。数据被分到红、黄、蓝三簇，每一类内部的油井彼此距离相近，不同类别之间的油井距离较远。

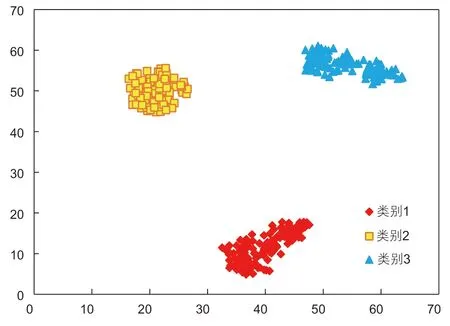
图5 聚类分析结果Fig. 5 The result of cluster

依据聚类分析结果，不同类别油井的平均单井日产油差异较大，如图6 所示。类别1 的油井产量较低，平均单井日产油水平在1 t左右，产量比较平稳；类别2 的平均单井日产油水平在2 t左右；类别3 的油井产量最高，平均单井日产油水平在5 t左右，产量波动明显。将每一类油井转换成一口典型油井。

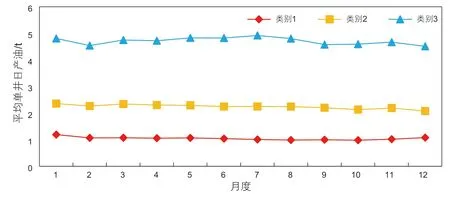
图6 不同类别油井平均日产油曲线Fig. 6 Average daily production curve of different types of wells

3.3 训练样本标注

3.3.1 样本标注流程

首先，通过油田开发生产现状分析，对油井进行聚类分组。针对每个油井分组，按照不同含水阶段，分别计算产量递减率和含水上升率；其次，针对每一口油井，从单井生产曲线上选择接近所属分组生产规律的阶段作为训练样本，主要考虑的指标为产量递减率和含水上升率。为了降低模型复杂度，不考虑措施增油阶段，只标注老井递减阶段；为了保证油井生产有一定的连续性，且符合油井产量人工智能预测算法的要求，选择连续生产时间不少于12 个月的生产阶段；单井产量递减率和含水上升率以所述油井分组的产量递减率和含水上升率为中心上下波动，通过计算机自动标注训练样本和专家手动标注训练样本的符合率来测算波动范围，如图7 所示。

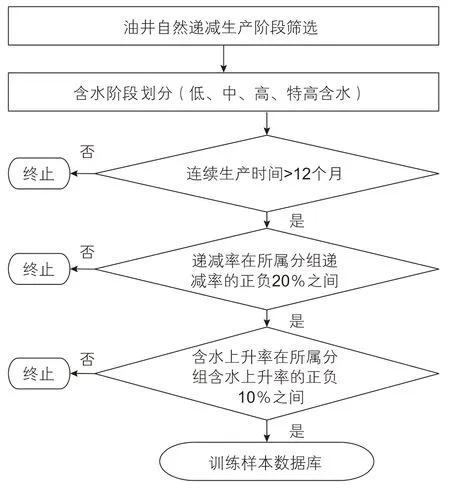
图7 样本标注流程Fig. 7 Sample annotation flow chart

3.3.2 建立样本集合

从每一分类中随机抽取30%的油井进行训练样本标注，针对抽样的油井按照不同含水阶段进行标注，一口井可以标注多个样本，共标注样本3500 个。按照机器学习中监督学习算法对训练样本的要求，构建模型训练需要的输入(x)和输出(y)。输入(x)为某一阶段的油井生产状态信息，包括日产油、含水率、流压、动液面、累产油和累产液等数据；输出(y)为下一阶段油井的日产油和含水率数据，如图8 所示。

图8 油井训练样本示意图Fig. 8 Schematic diagram of oil well training sample

3.4 产量预测模型构建

3.4.1 特征分析

依据水驱油田生产特征及油田开发历史数据，定性筛选出15 个特征：有效厚度、渗透率、井距、日产油、日产水、含水率、累产油、累产液、累产水、采出程度、静压、流压、泵深、冲程、冲次。

采用皮尔逊相关系数度量两个变量X和Y之间的相关程度，其值介于-1 与1 之间。相关系数的绝对值越大，相关性越强。绝对值在0.8 至1.0 之间表示极强相关；绝对值在0.6 至0.8 之间表示强相关。基于定性分析结果，采用皮尔逊相关系数进行定量分析。取相关性绝对值大于0.6 的特征作为模型的输入。确定模型输入的特征为日产油、日产水、累产油、含水率、流压、累产液和渗透率，如图9 所示。

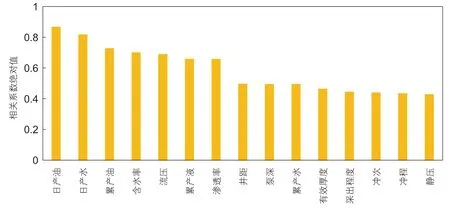
图9 特征相关性定量分析Fig. 9 Quantitative analysis of feature correlation

3.4.2 数据集划分

本文选取2020 年1 月至2020 年12 月的数据作为验证集，2021 年1 月至2021 年12 月的数据作为测试集，其余训练样本全部作为训练集。

为了保证模型训练与产量预测结果的稳定性，本文采用归一化处理方法，将其映射到[0,1]区间，线性变换式为：

3.4.3 模型训练

本文实验验证采用Tensorflow开源平台作为深度学习平台，采用Python 3.7 编写实验程序，同时使用了一些第三方库，如使用Sklearn、Numpy计算技术指标，使用Keras搭建网络结构。

选用长短时记忆神经网络算法作为模型的学习器。损失函数(loss function)使用均方误差(Mean Square Error, MSE)，计算方法表示为：

优化器(optimizer)使用“adam”，用来计算神经网络每个参数的自适应学习率。采用Dropout(按照一定的比例将神经元暂时从网络中丢弃)方法防止过拟合，Dropout的比例为30%。

由于不同油井在平面和纵向物性差异大，造成不同层系、不同开发阶段产量差异较大，而平均绝对百分误差(Mean Absolute Percentage Error，MAPE)通过计算相对值可以消除产量差异大的影响，因此本文采用相对误差(1-MAPE )作为模型精度评价标准。

针对训练样本，去掉实体名称(油田名和井名等)和生产时间，只按照生产年月的前后顺序保留每个实体的静态数据和生产动态数据，针对每个样本单独建立监督学习算法所需的训练样本。

采用文献[20]中的模型训练与自动调优方法，最终确定模型的主要超参数组合，如表1 所示。

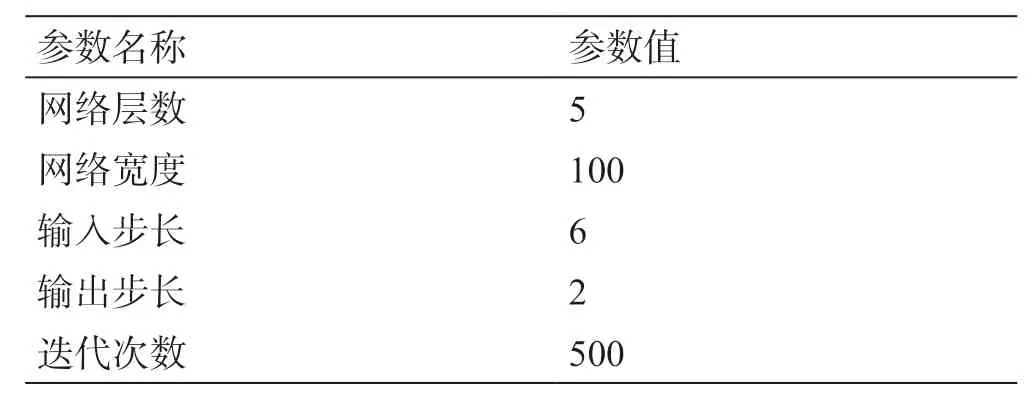
表1 模型主要参数Table 1 Main parameters of the model

3.4.4 产量预测

将3 口典型油井2020 年的日产油、日产水、累产油、含水率、流压、累产液和渗透率数据输入产量预测模型，得到未来三年的预测产油量，如图10 所示。

图10 油井产量预测曲线Fig. 10 Well production prediction curve

计算3 口典型井的年产油量，再分别乘以所属油井分组的井数，即可得到该油井分组的年产油量。与2021 年实际值进行对比分析，分组3 由于产量波动较大，年产量相对误差较大，达到7.5%；分组1 和分组2 的年产量相对误差分别为2.1%和3.9%；油田2021年产量的相对误差为5.6%，2022 年与2023 年产量缓慢递减，符合现场生产趋势，如表2 所示。

表2 实际产量与预测产量误差分析Table 2 Error analysis of actual production and prediction production

3.5 预测方法对比分析

为了验证本文方法的优越性，与以下3 种方法的预测结果进行对比：方法一：将该油田生产数据作为训练样本，利用机器学习方法建立油田产量智能预测模型，预测2021 年产量；方法二：将全部油井生产数据作为训练样本，利用机器学习方法建立油井产量智能预测模型，预测每口油井2021 年的产量，累加汇总成油田产量；方法三：利用水驱特征曲线预测油田2021 年产量。

从预测结果可以看出：方法一由于训练样本数量较少，模型建立时间短，预测精度不高，为87.8%；方法二需要对所有井进行样本标注，耗时最长，预测精度达到92.5%。对预测结果进行分析，发现部分关井、产量突然大幅波动的油井预测误差较大，从而降低了油田的预测精度；由于该油田处于特高含水阶段，方法三的预测结果出现了“上翘”现象，预测精度为92.1%；本文方法通过聚类分析，虽然减少了样本数量，但是增加了样本的代表性，缩短了时间，却提高预测精度，达到94.4%，如表3 所示。综上所述，本文方法适用于具有一定规模油井的油田产量预测，通过油井聚类分析增加训练样本数量，利用神经网络模型实现产量预测。

表3 不同方法预测结果对比Table 3 Comparison of prediction results of different methods

4 结论

机器学习是一项通用技术，应用到油田产量预测时，应结合油田生产特征和油田生产数据特点，灵活有效的构建机器学习所需要的训练样本数据，提高模型构建效率和预测精度。

(1)基于无监督学习的K均值聚类算法根据油井产量对油井递减趋势进行聚类，可以快速识别油井产量递减类型，使同一类别中的油井具有相似的产量变化规律，不同类别之间油井产量变化趋势差异较大；

(2)从每类油井中按比例随机抽取油井进行训练样本标注，与使用油田生产数据作为训练样本相比，可以增加机器学习所需的训练样本数量，提高模型预测精度；与使用全部油井生产数据作为训练样本相比，在保证预测精度的同时，可以减少数据处理工作量；

(3)通过分析油田开发历程及生产特征，剔除油井长期关井、数据异常等阶段，建立油井某一阶段的产量和与之对应的生产制度，有助于机器学习方法寻找产量和影响因素之间的因果关系，提高模型的预测精度；

(4)将具有相似产量变化趋势的一类油井转换成一口典型油井，使典型井可以代表该类井的生产特点，又可以降低单井产量的波动性，提高产量数据的平稳性，使产量预测结果更加准确。