基于注意力机制的无监督学习地震数据随机和不规则噪声衰减方法

杨柳青 ，王守东 *，杜宝强

1 中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249

2 中国石油大学(北京)海洋石油勘探国家工程实验室，北京 102249

0 引言

地震资料在采集时受环境和设备等因素干扰，导致在采集到的地震数据中产生大量噪声。野外采集到的信号通常由有效信号和干扰信号(噪声)构成，其中有效信号含有油气勘探和分析的重要信息。被强噪声覆盖的地震数据严重影响了地震资料的后续偏移和成像等处理。因此有必要开发一种高效且自适应的噪声衰减方法来提高地震资料的信噪比(Signal-to-Noise Ratio, SNR)。常规的地震随机噪声衰减方法经过几十年的发展大致可分为4 类，即基于预测滤波的算法，基于变换域滤波的算法，基于模态分解的算法和基于矩阵降秩的算法。Canales[1]提出f-x域预测滤波算法来衰减随机噪声，该算法基于有效反射信号的可预测性来实现。此外，还有t-x域预测滤波[2]和非平稳预测滤波[3]。基于变换域的噪声衰减方法通过设置阈值的方法来衰减地震数据变换到特殊域的噪声，这是利用有效信号与噪声在变换域的差异性来达到衰减噪声的目的。常见的变换域去噪方法有Seislet变换[4]，小波变换[5]和曲波变换[6]等。基于模态分解的去噪算法将含噪地震数据分解为多个成分，并从中筛选出有效信号的表示成分，最后通过叠加重构有效信号来达到衰减噪声的目的。具有代表性的模态分解方法有经验模态分解算法(Empirical Mode Decomposition,EMD)[7]和集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)[8]。基于矩阵降秩的去噪算法假设有效信号在频域的表示是低秩的，而噪声将提高有效信号低秩矩阵的秩。因此通过恢复低秩矩阵就可以重建有效信号，进而分离出噪声。常见的矩阵降秩方法有多道奇异谱分析(Multichannel Singular Spectrum Analysis, MSSA)[9]和阻尼多道奇异谱分析(Damped multichannel singular spectrum analysis, DMSSA)[10]。与服从高斯分布的随机噪声不同的是，异常值噪声具有高振幅的特点。

近年来随着计算机硬件和软件的发展，深度学习技术在地震勘探领域得到了广泛应用。深度学习技术利用大量非线性模块来建立源域与目标域数据之间的非线性映射关系[11]。在地球物理领域，深度学习技术已用于断层识别[12]、储层参数预测[13]和高分辨率处理[14]等。当前，研究学者已经将深度学习技术应用于地震数据中的随机噪声和高振幅异常值噪声衰减中，主要分为监督学习和无监督学习算法。对于监督学习算法，韩卫雪等[15]构建了一个卷积神经网络来衰减叠前地震数据中的随机噪声。随机噪声服从均值为零且方差为常数的高斯分布。王钰清等[16]在数据增强技术的基础上提出使用卷积神经网络对地震数据的噪声进行分离。滑世辉和韩立国[17]利用公开模型生成大量带有标签的合成数据并制作数据集来训练卷积自编码器，该框架在二维合成数据与实际地震数据中具有良好的随机噪声衰减表现。基于监督学习的框架需要人工构建标签来拟合网络，这将增加人力成本。对于三维地震数据，大量带有标签的数据集将带来巨大的计算成本。宋辉等[18]提出一种无监督卷积自编码器来衰减二维地震数据中的随机噪声，该框架无需生成标签即可自适应地提取出有效反射信号。Saad and Chen[19]提出一个基于自编码器的无监督框架来衰减随机噪声，在多个合成和实际地震数据中取得了比传统算法更优的效果。目前基于深度学习的随机噪声衰减框架大多利用均方根误差(MSE)损失函数来训练网络。对于具有高振幅特性的异常值噪声，其频率直方图近似拉普拉斯分布曲线。Qian等[20]提出一个卷积自编码器来衰减二维地震资料中的随机和异常值噪声，该算法采用Welsch损失函数来衰减异常值噪声。Wang等[21]提出一种基于监督学习的注意力卷积神经网络来衰减异常值噪声，该算法以噪声为学习目标来分离出有效信号。面对日益精细的高精度勘探，开发一个高效且自适应的无监督框架来处理多维地震资料中的噪声非常重要。

为了提高多维地震数据的随机噪声衰减效率和自适应性，本文基于无监督学习策略构建了一种带有注意力机制的随机和异常值噪声衰减框架。该框架采用全连接层作为主要的特征提取层。编码器和解码器分别由带有多分支特征提取能力的注意力块构成。为了增强浅层级至深层级之间的特征传递以避免丢失重要特征，我们在对应的编码与解码器之间增加一个跳跃连接机制。我们采用有助于保持地震波形横向连续性的数据增广方法来分割地震数据以扩充训练样本数量。为了更有效地衰减异常值噪声，我们采用对异常值噪声更具鲁棒性的Huber损失函数来衰减随机和异常值噪声，该损失函数结合了带有l2范数的均方根误差和l1范数的平均绝对误差损失。此外，在构建的网络中加入总变分(Total Variation, TV)正则化项来捕捉地震资料局部的光滑结构。通过实验调整Huber损失函数与TV正则化项的权重，从而使得网络获取最佳的去噪表现。二维和三维的合成与实际数据测试表明：相比传统的地震噪声衰减算法和先进的无监督深度学习算法，本文提出的框架具有更好的噪声衰减与有效信号提取性能。

1 理论方法

1.1 全连接特征提取结构

无监督自编码器的去噪过程是对受损数据的重建，利用迭代的方式从含噪数据中提取重要特征的表示。利用编码器和解码器对数据进行压缩和重构来提取特征和去噪。在编码阶段，含有多个神经元的编码器对含噪数据进行数据压缩以提取抽象的特征表示。在解码阶段，高阶抽象特征被多个含有不同数量神经元的解码器重构为去噪后的数据。

在多维地震数据随机噪声衰减中，有效反射信号y可以表示为：

其中，x表示为含噪数据，n表示地震数据中包含的噪声。我们旨在采用一种自适应的方式从受损坏的地震数据x中重构出干净数据y。

我们提出的多分支注意力去噪网络(multi-branch attention denoising network, MADNet)是一个端到端的无监督学习框架，即无需人工生成标签来训练网络。MADNet由多个编码器和解码器构成，其中每个层级中对应的编码器和解码器之间都含有一个跳跃连接层。这种结构类似于浅层级与深层级中添加了一个残差连接结构，这有助于在深层级中迁移并重用浅层级提取到的重要特征。该框架采用全连接层(Fully Connected Layer, FCL)作为主要的特征提取层，具体结构如图1中的线框A所示。编码阶段中全连接特征提取块在第i个全连接层输出Oei可表示为：

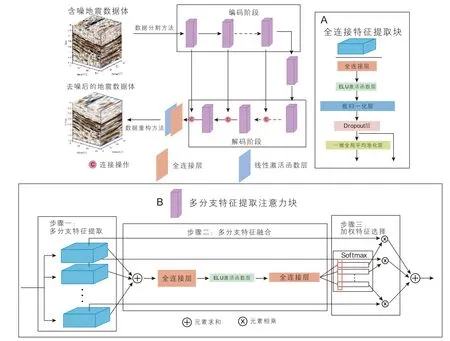
图1 多分支注意力去噪网络结构示意图Fig. 1 The structure of multi-branch denoising framework

其中，Wei和bei网络在编码器阶段e中该全连接层需要学习的权重和偏置，X表示输入的含噪样本。

含噪数据经过全连接层后，我们采用非线性激活函数将Oei转换为非线性模式以增强非线性映射能力。本文采用ELU激活函数，经过非线性转换后编码器的输出Rei可表示为：

其中α表示ELU激活函数，表达式为：

随着迭代次数和层级的增加，网络容易造成误差累积。为了减少由协变量偏移导致的误差累积，我们在非线性激活函数层后加入批归一化层(Batch Normalization, BN)[22]来修正偏差并提高网络的收敛速度，它可以表示为：

其中，μ和σ2分别表示均值和方差，δ和γ分别表示BN层的可训练参数,ε表示用于防止为0 的固定值。为了避免网络在迭代过程中出现的过拟合现象，我们在BN层后添加一个dropout层。最后我们添加一个一维全局平均池化层来编码先前提取到的特征，该层可表示为：

全连接特征提取块采用非线性操作将线性特征提取转换为非线性模式。全连接层有助于提取输入地震数据的全局特征。MADNet中采用BN层和dropout层来减少过拟合现象和神经元之间特征的依赖，进而起到了正则化的作用。

1.2 多分支特征提取注意力块

为了增强网络在计算过程中对重点区域的关注程度，注意力机制[23]受到了研究人员的广泛关注。注意力机制通常分为软注意力(Soft Attention)，硬注意力(Hard Attention)和自注意力 (Self Attention)。本文提出的框架采用带有软注意力机制的多分支特征提取注意力块来提取重要的波形特征。相比硬注意力，软注意力利用加权的方式通过前向训练和后向反馈实现对重要的特征信息进行关注。Li等[24]提出一个基于卷积神经网络的多尺度注意力机制来提取不同感受野的特征。我们构建了一个多分支特征提取模块作为MADNet主要的波形特征提取结构，如图1 的线框B所示。经过全连接特征提取块后，我们添加两个全连接层进行特征融合，即将先前由多个分支提取到的特征信息相融。特征融合阶段可以表示如下：

其中，pe表示先前多分支提取的特征的融合，W1和W2分别表示第一个和第二个全连接层的权重矩阵，b1和b2分别表示第一个和第二个全连接层的偏置向量，α表示ReLU激活函数。特征融合阶段后我们采用加权的方式对特征提取和特征融合阶段进行特征选择。Softmax函数被用来从前层中选择重要信息，多分支特征提取注意力块的输出可以表示为：

跳跃连接是在不同层级中添加一个恒等映射的连接机制，用来提升网络的鲁棒性和特征迁移能力。随着研究的深入，研究人员发现神经网络的性能并非随着层级加深而提高。相反，当层级加深至一定程度，其非线性映射能力将出现退化，即出现梯度消失等现象。He等[25]提出了ResNet来解决由于网络层级加深而导致的精度饱和问题。为了提升浅层与深层级网络的特征共享与迁移能力，我们在搭建的MADNet中加入跳跃连接机制，如图1 所示。

1.3 无监督学习策略与网络结构

本文提出的MADNet使用含噪数据即可利用迭代的方式实现自适应地震数据去噪。Ulyanov等[26]提出一种自监督去噪策略来衰减图片噪声，该策略基于l2范数实现。对于地震数据中的随机噪声和异常值噪声衰减，我们采用均方根误差函数和平均绝对误差函数的Huber函数作为损失函数，可以表达为：

其中，ΓNet表示提出的MADNet, ΓNet(x; )θ表示去噪后的地震数据，θ表示网络需要训练的参数，x表示含噪地震数据，c表示Huber函数中的调谐参数。接下来，我们在损失函数中加入TV正则化项来捕捉地震数据局部的光滑结构，TV项可以表示为：

其中∀表示梯度算子。最后我们通过合并两个损失函数并使用β来分配各自的权重，β为0.9。总损失函数可以表示为:

在迭代过程中为了使网络达到最佳的训练状态，我们采用了两个优化策略。一个是早停止优化策略，即当验证集损失连续5 次迭代不下降时保存先前得到的最优模型和参数。另一个是自适应学习率优化策略，即每经过20 次迭代，学习率将下降一倍。为了加速网络收敛并优化网络训练的权重矩阵和偏置，我们采用善于处理稀疏梯度和非平稳目标的Adam[27]优化算法。

本文搭建的MADNet是一个端到端的无监督框架，共包含全连接特征提取块和多分支特征提取注意力块，如图1 所示。我们共采用3 个编码器和3 个解码器分别对含噪数据进行降维提取波形特征和恢复数据尺寸。每个多分支特征提取注意力块中包含两个并行计算的全连接特征提取块，在编码阶段，从顶端到低端的全连接特征提取块中全连接层的神经元数量分别为64,32 和16。在解码阶段，全连接特征提取块中全连接层的神经元数量分别为16,32 和64。在构建的网络中间我们添加了一个全连接层中神经元数量为8 的多分支特征提取注意力块。每个对应的编码器与解码器之间添加了跳跃连接机制，该全连接块中全连接层的神经元数量与对应层级的编码器和解码器一致。此外，在多分支特征提取注意力块的特征融合阶段还包含两个全连接层，其神经元数量分别为当前层级全连接特征提取块中全连接层的神经元数量的四倍和原始值。

2 数值测试

2.1 数据预处理及去噪表现评估方法

本文构架构建的网络使用单个含噪地震数据作为输入。然而，大尺度地震数据输入到网络中难以有效的被提取局部特征。本文采用小尺度数据分割技术[28]将大尺度二维或三维地震数据分割为大量一维小尺度地震信号。小尺度数据分割技术有两个主要参数来控制数据的分割维度。如图2 所示，以二维数据分割为例：一个是分割尺寸P，即将数据分割为P×P尺寸的一维数据；另一个是滑动尺寸，即分割窗口沿空间和时间的位移大小。假设分割和滑动尺寸为40 和1，原始含噪数据尺寸为496 ×48 的数据经过分割后生成4113组1600 ×1 的一维数据。大量小尺度数据经过噪声衰减后，我们采用数据重构技术将去噪后的一维信号恢复至原始地震数据尺寸，重构流程如图2b所示。小尺度数据分割技术有助于保持数据的波形横向连续性。

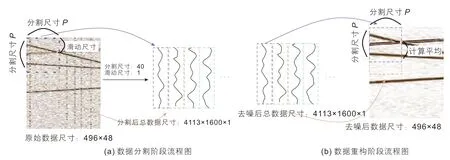
图2 小尺度数据分割技术流程图Fig. 2 Flow chart of small scale data segmentation technique

由于实际数据缺乏干净的标签，因此难以使用信噪比(SNR)进行定量的对比。在本文中我们采用两种评估方法来评价合成数据和实际数据的去噪效果，分别为SNR对比和局部相似性检测。SNR的公式表达如下所示:

其中，y无噪数据，ΓNet(x; )θ表示去噪后的地震数据。另一个去噪效果评价方式是局部相似性对比[29]。该方法可以通过计算移除的噪声与去噪后数据的局部相似度来检测去噪数据中的有效信号泄露情况。

2.2 二维地震数据测试

本文提出的方法是一种基于无监督的噪声衰减框架，即无需制作标签来拟合网络。为了测试网络在二维地震数据中的去噪表现，我们首先采用二维合成数据进行去噪实验。无噪数据如图3a所示，该数据的时间采样间隔为4 ms。含噪数据和添加的噪声如图3b和3c所示，其中含噪数据的SNR为-3.44 dB。为了验证提出的网络的去噪有效性，本文采用DMSSA[10]和一个无监督深度学习框架(PATCHUNET)[19]作为对比方法进行二维地震数据去噪测试。

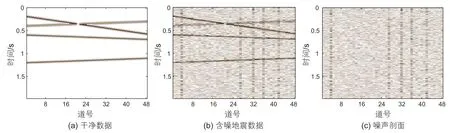
图3 二维合成地震数据Fig. 3 2D synthetic seismic data

PATCHUNET与本文提出的MADNet具有相同的底层框架，即采用编码和解码的结构来压缩和重构地震数据。图4 展示了3 种方法的去噪结果，从中可以看到DMSSA(图4a)中存在大量未去除的噪声。MADNet相比DMSSA的去噪数据更干净且同相轴更清晰。本文提出的方法与PATCHUNET的去噪后地震数据相似，难以直观的分辨出差异。图4d～f展示了三种方法移除的噪声剖面，DMSSA方法移除的噪声剖面中存在明显的有效信号，表明存在有效信号损失问题。从视觉中本文提出的方法和对比方法都能较好的衰减噪声。3 种方法的SNR如表1 所示，DMSSA、PATCHUNET和MADNet的SNR分别为8.57 dB、9.45 dB和10.32 dB。本文提出的方法相比DMSSA和PATCHUNET的SNR分别提高了1.75 dB和0.87 dB。评价去噪方法的优劣不仅是噪声衰减能力，还需要从信号保护能力来看。为了进一步检测三种方法的有效信号泄露情况，我们绘制了局部相似性图。图5 展示了三种方法由去噪后的数据和移除的噪声计算得到的局部相似性对比图。色标颜色越深则表示信号泄露越严重。相比MADNet(图5c)的检测结果，DMSSA(图5a)的局部相似性图在0.5～0.8 s的范围存在高能量区域，表明更多的有效信号泄露。PATCHUNET的局部相似性对比图(图5b)显示同相轴附近出现明显的有效信号能量。评价不同方法的去噪表现需要从去噪后的数据，移除的噪声和信噪比这三方面来衡量。从3 种方法的二维合成数据去噪结果来看，本文提出的MADNet具有最高SNR，即10.32 dB。从去噪后的数据中来看，MADNet重构后的同相轴更加清晰且包含的噪声更少。

表1 三种网络在二维合成数据测试中的信噪比对比Table 1 Comparison of the SNR using three networks in 2D synthetic data testing

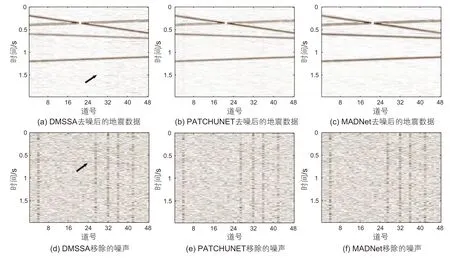
图4 三种不同方法的去噪效果对比Fig. 4 Denoising comparison using three different methods

为了进一步验证本文提出的网络的去噪效果，我们使用二维实际地震数据进行测试。实际地震数据如图6 所示，该数据曾被Chen等[30]用于噪声衰减。从实际数据中可以看到大量反射信号被噪声严重覆盖。DMSSA、PATCHUNET和本文提出的网络的去噪结果如图7 所示。图7a～c展示了3 种方法去噪后的地震数据。从图7a中可以看到DMSSA的去噪数据过于平滑。反观PATCHUNET和MADNet，其去噪剖面在衰减噪声的同时没有改变构造的细节。在图7a中，DMSSA去噪后地震剖面的局部区域出现微断裂，这在实际地震数据中被噪声严重覆盖。在图7c中本文提出的MADNet不仅可以有效的衰减强噪声，还可以清晰的重构出有效信号。图7d～f展示了3 种方法移除的噪声剖面。相比DMSSA，本文提出的MADNet的噪声剖面中的有效信号更少。从图7d中可以看到明显的高振幅数据泄露问题。对比图7e和图7f，本文提出的MADNet在移除的噪声剖面中具有更少的有效信号。

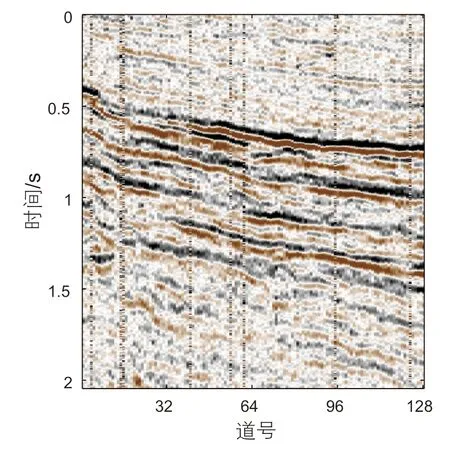
图6 二维实际地震数据Fig. 6 2D field data

图7 三种不同方法的去噪效果对比Fig. 7 Denoising comparison using three different methods

2.3 三维地震数据测试

本文提出的方法的特征提取层为全连接层。三维地震数据输入网络前使用小尺度数据分割技术将其分割为大量一维数据以提高训练效率。输入的三维地震数据如图8 所示，其时间采样为4 ms。含噪数据如图8b所示，其SNR为-2.47 dB。本次测试采用一种字典学习算法(SGK)[31]和优化阻尼降秩(ODRR)[32]作为对比方法。我们采用的分割和滑动尺寸为15 和1，共生成36 288 个一维样本输入到网络中进行训练。

图8 三维合成地震数据Fig. 8 3D synthetic seismic data

3 种方法的去噪结果如图9 所示，其中图9a～c为SGK、ODRR和MADNet的去噪数据。从SGK(图9a)的去噪数据中可以看到同相轴的连续性较差且不清晰。ODRR的去噪数据如图9b所示，去噪后的数据体中仍残留未衰减的噪声。相比两个对比方法，本文提出的MADNet重构的波形特征更加清晰且残留的噪声较少，与干净数据(图8a)最接近。从重建后的地震数据来看，MADNet几乎看不到明显的噪声残留。图9d～f展示了3 种方法移除的噪声。相比SGK和ODRR，MADNet移除的噪声包含更轻微的有效信号，表示在去噪过程中对有效反射信号的损害最小。接下来从数值的角度来对比3 种方法的去噪表现，如表2 所示。SGK、ODRR和MADNet的SNR分别为8.89 dB、9.44 dB和10.43 dB。相比两个对比方法，本文提出的网络具有高的SNR。为了进一步检测三种方法在去噪过程中的信号泄露情况，我们绘制了3 种方法的局部相似性对比图，如图10 所示。从图10b中可以看到SGK的有效信号泄露问题相比剩余两种方法较大。ODRR和MADNet的局部相似性对比图结果接近，即检测到的有效信号能量相似。综合两个对比方法和本文提出网络的去噪表现，MADNet在衰减噪声时可以更好的保护有效信号。

表2 三种网络在三维合成数据测试中的信噪比对比Table 2 Comparison of the SNR using three networks in 3D synthetic data testing

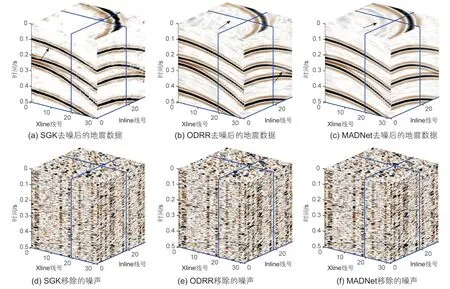
图9 三种不同方法的去噪效果对比Fig. 9 Denoising comparison using three different methods

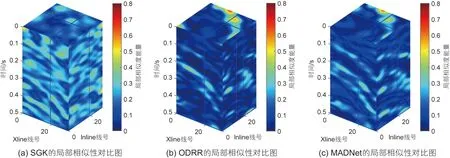
图10 三种不同方法的局部相似性对比图Fig. 10 Comparison of local similarity maps using three different methods

为了进一步验证本文提出的网络在三维地震数据中的去噪表现，我们将算法应用到实际地震数据中，并与SGK和ODRR算法进行对比。我们采用小尺度数据分割技术将三维实际地震数据分割为一维含噪信号输入到网络中进行训练。这里的一维信号表示沿三维地震数据的各个方向根据分割和滑动尺寸分割得到。小的分割尺寸将生成更多的小尺度数据，这将增加训练时间。选择合适的分割和滑动尺寸将不仅可以提高训练效率，还可以提升去噪表现。如图11 所示，该数据先前被Wang等[33]用于随机噪声衰减测试。实际地震数据体中的有效反射信号被噪声严重覆盖，难以观察到反射信号。本文提出的方法和对比方法的去噪结果如图12 所示。图12a～c展示了SGK、ODRR和MADNet去噪后的地震数据。从SGK(图12a)的去噪数据可以看到重构后的地震信号受到了损坏。ODRR(图12b)去噪后的地震数据衰减掉了大部分噪声，但重建后的地震信号过于平滑。从图11c中可以看到本文提出的MADNet不仅衰减掉了大部分随机噪声，而且有效的恢复了反射信号。图12d～f展示了3 种方法去除的噪声。对比3 种方法去除的噪声，ODRR的有效信号泄露问题相比提出的MADNet更加严重。SGK方法移除的大量噪声，但仍能从移除的噪声看到高振幅的有效信号。

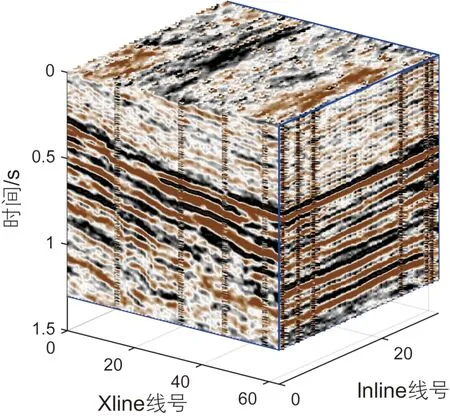
图11 三维实际地震数据Fig. 11 3D field data

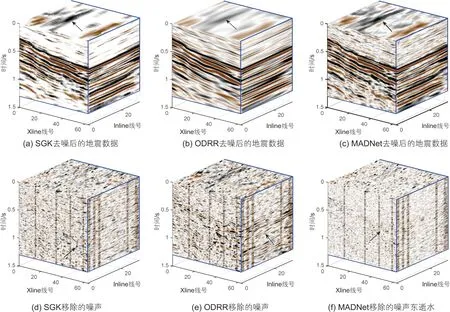
图12 三种不同方法的去噪效果对比Fig. 12 Denoising comparison using three different methods

2.4 讨论

深度学习技术通常分为监督和无监督两种方式，本文构建了一种基于无监督的框架来衰减多维地震数据中的随机噪声。由于实际数据难以制作干净的标签，因此监督学习框架受到了标签的限制。实际应用时，使用小尺度地震数据分割技术将含噪数据分割为大量一维地震数据直接输入到网络中即可自适应的完成去噪工作。本文使用提出的网络在二维和三维的合成以及实际地震数据中进行了测试，该网络同样可以对更高维度的地震数据进行去噪处理。为了测试本文提出的方法的鲁棒性，我们在二维和三维合成地震数据中添加不同水平的噪声进行去噪测试。测试结果如图13 所示，图13a和13b分别为本文提出的方法和对比方法在二维与三维合成地震数据中的降噪结果。图13a中的黑色、红色、蓝色和紫色线条分别表示含噪数据DMSSA、PATCHUNET和MADNet的去噪结果。从图中可以看到本文提出的方法相比两个对比方法有最高的信噪比。在强噪声背景下，本文提出的方法依然可以有效的提高地震数据的信噪比。图13b展示了3 种方法在三维合成地震数据中的去噪结果。与二维合成地震数据去噪表现一致，本文提出的网络有最佳的去噪表现。小尺度地震数据分割技术有助于提高波形特征的提取。

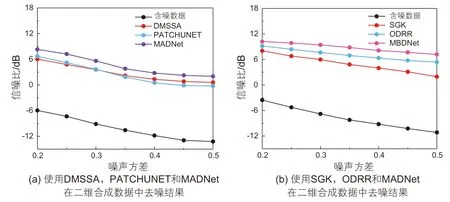
图13 二维和三维合成数据中不同水平噪声下不同方法的去噪表现Fig. 13 Denoising performance of different methods on different noise levels of 2D and 3D synthetic data

本文提出的MADNet的主要结构为多分支特征提取注意力块，该结构通过特征提取、融合和选择对重要的波形特征提供更大的权重。为了验证注意力块在噪声衰减中的作用，我们通过消融实验进行对比。不含注意力机制的MADNet中的注意力块由全连接特征提取块组成，包含一个全连接层，一个激活函数层，一个批归一化层和一个dropout层。图14 展示了本文提出的MADNet和不含注意力机制的MADNet在二维和三维合成数据中的训练和验证集损失对比。从训练集损失的迭代曲线可以看出含有注意力机制的网络具有更低的误差。对于二维合成数据，MADNet和不含注意力机制的网络的训练参数分别为519 168 和317 896。从训练效率来看，MADNet不含注意力机制的网络的训练时间分别为134 秒和51 秒。为了进一步展示两种网络的去噪效果，我们在图15 和图16 分别展示了在二维和三维合成数据中的去噪结果。对比图15 中两种网络移除的噪声剖面和局部相似性图，含有注意力机制的网络具有更好的保幅性。两种网络的SNR分别为8.98 dB和10.32 dB。从图15 的两种网络在三维合成数据去噪结果的对比中，可以看到含注意力机制的网络去噪后的地震数据中残留的噪声更少。两种网络去噪后数据的SNR分别为7.33 dB和10.43 dB。综合去噪后的地震数据和移除的噪声，含有注意力机制的网络在去噪性能和保幅性中均具有更好的表现。

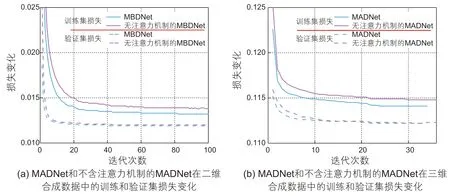
图14 不同网络结构的损失曲线对比Fig. 14 Comparison of loss curves using different network structures

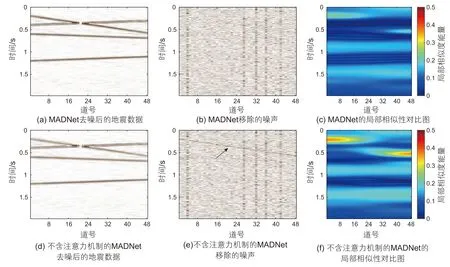
图15 二维合成数据中不同网络结构的去噪效果对比Fig.15 Comparison of denoising performance using different network structures on 2D synthetic data

图16 三维合成数据中不同网络结构的去噪效果对比Fig. 16 Comparison of denoising performance using different network structures on 3D synthetic data

3 结论与认识

本文针提出了一种无监督学习框架来衰减多维地震数据中的随机和异常值噪声，该网络无需生成干净的标签来拟合网络。我们使用小尺度地震数据分割技术将多维含噪地震数据分割为大量一维数据并输入到网络中进行迭代。本文所构建的框架使用全连接层来提取波形特征，并采用多分支特征提取注意力块以加权的方式来分配权重，进而提高网络对重要特征的提取能力。本文提出的网络分为编码和解码两个阶段，其中编码层用于压缩数据并提取抽象特征，解码层用于进一步提取特征并重构特征。为了更有效的衰减异常值噪声，本文采用对异常值噪声更具鲁棒性的Huber损失函数来衰减随机和异常值噪声。此外，在构建的网络中加入总变分正则化项来捕捉地震资料局部的光滑结构。二维和三维合成与实际地震数据的测试结果表明本文提出的框架可以有效的衰减噪声。相比经典的地震数据去噪方法和无监督去噪方法，本文提出的方法具有更好的噪声衰减和同相轴重构能力。通过对含有不同水平噪声地震数据的衰减测试，实验结果表明本文提出的方法具有良好的鲁棒性。