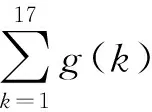基于认知分析的数学问题深度教学——以一道函数试题的认知分析与深度教学为例

尤 娜, 周 浪, 赵思林

(1.重庆师范大学 数学科学学院, 重庆 401331;2.自贡横川实验学校,四川 自贡 643000;3.内江师范学院 教育科学研究院, 四川 内江 641100)

学习的本质是认知．数学学习是基于问题和问题解决的认知过程．数学问题是数学深度教学的“心脏”．数学深度教学是以数学问题的认知分析为基础、指向学生深度学习和数学核心素养生成的教学．数学问题及其解决唯有对其实施深度教学,才更能促成学生的主动学习和深度学习,从而充分发挥问题和问题解决教学的育人效果．2024届某市高三第一次诊断性考试数学试题(理科)第16题(以下简称试题)是一个值得深度教学的好问题．从问题价值、问题解决的认知障碍及学生已有数学认知经验分析该问题,并从深度理解、多元表征、知识迁移、发现创新等角度提出数学问题的深度教学建议．

1 试题简介

对一个省级一级学校高三某班的测试情况做了调查,该班数学平均成绩是128分,但该试题的得分率仅为53.19%,是全部选填题中得分率最低的．另调查了其他学校高三3个不同层次班级的考试情况(此次数学平均成绩分别为98.7、106.2、114.6),它们的得分率都低于35%．这说明,该试题对很多学生都具挑战性且有相当难度．从学生考试结果看,该试题是一个令学生有较大困难的问题．因此,研究以该试题为载体的深度教学富有意义．

2 数学问题的认知分析

数学问题的认知分析包括数学问题的价值分析、问题解决的认知障碍分析以及学生已有数学认知经验分析等．

2.1 数学问题的价值分析

高价值问题是激发学生学习动机的重要资源,也是教师实施深度教学的优质资源．学生对数学问题的价值判断属于认知评价范畴,是一种高阶认知能力．教师和学生能够正确判断一个问题是否具有高价值性,是教师和学生跳出题海、精讲精练、落实“双减”的有效方法．高价值问题体现在培养学生数学核心素养的高价值性．学生只有认识到问题的探究价值和创新价值,才能有对问题主动探究和创新的欲望．教师只有认识到某个问题及其解决的育人价值,才会投入较多精力研究该问题及其教学．一个数学问题是否具有探究价值和育人价值主要从知识的价值性、问题的探究性、方法的普适性、思想的深刻性、思维的创造性等方面去评判．就本题而言,该试题以2个抽象函数为载体设问,意在考查函数的基本性质(奇偶性、周期性、对称性)、函数值、函数图象、复合函数、函数方程、求和符号等基础知识,考查函数与方程、数形结合、特殊与一般、化归与转化、代换法、构造法、消元法、赋值法、等价变换法等多种数学思想方法,考查分析问题、解决问题、创新意识等关键能力,考查数学抽象、逻辑推理、数学运算、直观想象、数学模型等核心素养．因此,该试题是一个考查学生函数重要知识、关键能力、创新意识和核心素养的高价值问题．

2.2 问题解决的认知障碍分析

学生对该试题形成认知障碍的主要原因是试题本身难度较大、学生对该试题的认知加工负荷远超工作记忆容量的上限(9个组块)、学生对解决该类问题所需认知经验不足等．具体表现为学生对该试题的数学知识的深度理解有困难,或数学思想方法的迁移有障碍,或解决该试题所需的创新素养不足,或上述情况兼有之．试题条件多且复杂,共含6个已知条件:f(x)的定义域为R,g(x)的定义域为R,f(-x)=f(x+6),f(2-x)+g(x)=4,g(x+1)为奇函数,f(2)=3．多数学生虽能单独理解这些条件中某个具体条件的含义,但不能综合地、整合性地分析和加工所有条件所蕴含的全部信息,更不能全部地深度理解它们的数学本质．由此就难以产生对数学知识和思想方法的有效迁移,更缺乏产生解决复杂问题所需的创新意识和创新能力．

2.2.1 对“f(-x)=f(x+6)”的认知障碍分析

学生难以对“f(-x)=f(x+6)”进行代数与几何的多元表征(等价变换的表达),如下面的无穷多个等价的表征(表达):

f(-x)=f(x+6)⟺f(x)=f(6-x)⟺f(3+x)=f(3-x)⟺

函数f(x)的图象关于直线x=3对称⟺

…

一些学生仅仅记忆了上述某些结论,未必真正理解和掌握其背后隐藏的数学本质．这是由于很多老师仅要求学生记住相关结论,不要求学生自己发现和证明相关结论,也就是说,学生未必知道这些结论成立(充要条件)之所以然．

2.2.2 对“g(x+1)为奇函数”的认知障碍分析

学生难以合理转化“g(x+1)为奇函数”条件加以运用．事实上,学生若不能将“g(x+1)为奇函数”等价转化为g(-x+1)=-g(x+1),或g(x)=-g(2-x),或函数g(x)的图象关于点(1,0)对称等形式,则后续的工作就较难开展．因为,该试题的解题关键是找到f(x)与g(x)的代数关系,而该条件的等价形式g(x)=-g(2-x)是找到f(x)与g(x)的代数关系的关键．如果把g(x)=-g(2-x)代入f(2-x)+g(x)=4中,就可得到f(2-x)-g(2-x)=4,再用x代换2-x,则有f(x)-g(x)=4．此外,对“g(x+1)为奇函数”的认知理解,需要一个认知操作的过程,就是通过“函数换元”来完成,即,若令G(x)=g(x+1),则G(x)为奇函数．因此必恒有关系G(-x)=-G(x)．从而可得到,g(-x+1)=-g(x+1);亦可得到,函数g(x)的图象关于(1,0)对称．

2.2.3 对“f(2-x)+g(x)=4”的认知障碍分析

学生对条件f(2-x)+g(x)=4的使用,容易产生无目标(方向)之感．事实上,此函数方程到底有什么作用,学生不太清楚．若孤立地考虑这个函数方程,则会一无所获．因此,学生应把下面三个函数方程结合起来考虑,即把

f(-x)=f(x+6),

①

f(2-x)+g(x)=4,

②

g(-x+1)=-g(x+1)

③

结合起来,做系统地思考与探究,并希望找到(发现)f(x)与g(x)的最简关系．对此,一种思路是把①往②代,一个自然的想法是由①构造出f(2-x),则有

f(2-x)=f(x+4),

④

然后,把④代入②得,f(x+4)+g(x)=4．此式与②好像差不多,可能感觉到这种思路行不通．另一种思路是把③往②代,一个自然的想法是由③构造出g(x),则有

g(x)=-g(2-x),

⑤

把⑤代入②可得,f(2-x)-g(2-x)=4．此方程等价于f(x)-g(x)=4．

⑥

到此,试题已经比较明朗了,因为已经找到了f(x)与g(x)的最简关系．但此时,很多学生仍不能发现方程⑥的本质和几何意义．事实上,方程⑥的本质主要有两个:一是方程⑥对∀x∈R都成立,即⑥是一个恒等式(注意:学生不容易理解),由此可猜想(或感觉到):f(x)与g(x)具有相同(类似)的性质,如它们的单调性相同、周期性相同、奇偶性类似;二是方程⑥的几何意义是f(x)的图象比g(x)的图象恒高4个单位．下面考虑通过⑥消去f(x)或g(x),探索f(x)和g(x)更多的性质,有下面的思路:由②和⑥消去g(x);由⑥解出f(x),并代入①消去f(x);充分运用g(x)的几何意义．处理该条件时,学生先后经历缺乏思路和多个思路的探究过程,由于认知经验不足,使学生因目标的不确定性而难以做出正确处理;由于创新素养不够,使学生因思路的多样性而难以择优做出正确选择．无论是解题思路狭窄的盲目处理,还是解题思路多样的择优处理,都自然会增加学生认知加工负荷．

2.2.4 对题目条件整合的认知障碍分析

数学问题的解决一般需要对题目所有条件进行整合性加工．但整合性加工容易产生认知障碍．这是由于脑科学研究发现,人的大脑同时接收到多个复杂信息时,大脑容易产生“死机”或“关机”现象．对试题而言,学生对题干中众多符号的认知加工负荷远超过工作记忆容量的上限(9个组块),一般会产生认知障碍．又由于题干涉及的符号多达10个:

这里我们把每一个符号只看成工作记忆加工的1个组块,已经远远超过了普通成人工作记忆加工平均“7个组块”的认知加工能力,这必然会给学生造成工作记忆加工超负荷的状况．此外,当学生同时面对“f(-x)=f(x+6)”“f(2-x)+g(x)=4”“g(x+1)为奇函数”这三个条件,或同时面对函数方程①②③时,由于它们各自表征方式的多样性和组合形式的多样性,导致学生恰当选择某些表征形式或组合具有盲目性和困难性,这必然容易给学生造成认知加工障碍．

2.3 学生已有数学认知经验分析

数学活动经验的获取必须经历心智操作和心力操作[1]．但学生常常获得的是没有充分通过心智操作和心力操作的“准经验”,这些“准经验”虽已进入学生的认知经验系统,但难以迁移到新问题情境之中去解决问题．据了解,在考前4位教师都详细讲解过2022年全国高考乙卷12题(以下简称高考题):

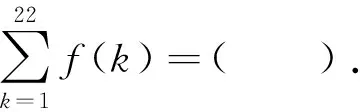
A．-21 B．-22 C．-23 D．-24

前述试题与此高考题相比较,它们的命题立意、题设条件(均为6个)、情境载体(两个抽象函数)、涉及函数性质(对称性、周期性)、两个函数方程、问题形式(求和符号)、解题方法等都比较相似．但该试题的得分率却惨不忍睹,说明学生并未真正理解高考题的数学本质,因此解答高考题的经验难以实现迁移．从学生认知经验的角度看,主要有两个原因．一是学生的已有经验是零碎且不系统的,需要把已有零碎经验系统化．调查发现,很多学生对f(-x)=f(x+6)产生了“懂而不会”的现象．究其原因是很多学生对结论的“懂”是一种比较粗浅的懂(仅限于“初步理解”的程度),很可能还含有一些似是而非的“懂”而并非“真懂”,这里的“不会”是指学生不会灵活运用知识即不会迁移．二是学生的已有经验不完备、不充足,解决问题时需要创造新的经验,但长期的“刷题”训练抑制了学生创造新经验的意愿和能力．如,高考题中的函数f(x)的一个周期为T=4且f(1),f(2),f(3),f(4)的值都能计算出来,但问题中的函数g(x)的一个周期为T′=8并且g(1),g(2),g(4),g(5),g(6)都能计算出来,但g(3),g(7)都不能计算出来并且g(3),g(7)有一个隐蔽的关系即g(3)+g(7)=0,这个隐蔽关系并非显然,甚至需要创新思维(整体思维)才能发现．因此,针对学生认知经验系统中的“准经验”,还需要整合碎片经验,反省片面经验,创造鲜活经验,升华价值经验,从而形成数学素养[2]．

3 数学问题的深度教学

数学问题的深度教学是指向学生深度学习的教学．数学深度学习的本质是学生获得数学的高阶思维和关键能力[3]．而数学高阶思维和关键能力是数学核心素养的重要成分．因此,深度学习是数学核心素养生成的必经途径,深度教学是数学核心素养落地的有效途径．学生深度学习和数学核心素养生成的过程是基于学生深度理解、多元表征、知识迁移、发现创新等自组织过程[4]．因此,数学问题的深度教学是指向学生深度理解、多元表征、知识迁移、发现创新的教学．

3.1 指向深度理解的教学

深度教学是指向学生对数学知识深度理解的教学．深度理解主要包括对数学语言(包括普通文字语言、数学概念语言、符号语言、图表语言等[5])、数学逻辑关系(如命题、性质等)、数学思想方法等的理解．深度理解要求能多角度地理解数学知识,建立新知识与其他已有知识之间内在的、本质的联系,感悟数学知识内蕴的数学思想方法．就试题而言,深度理解主要包括对函数概念和符号、函数方程或方程组、消元法、问题系统中关键要素的深度理解．

指向数学知识深度理解的教学,教师要注意以下几个方面:其一,对数学概念的内涵、符号及几何意义的准确理解.如对“g(x+1)为奇函数”的深度理解应包括对奇函数定义的理解、其代数关系(函数方程)的多种表征、复合函数g(x+1)的正确认识与理解．其二,学生对三个函数方程①②③的深度理解是整个问题深度教学的难点.具体包括以下几点:一是函数方程①②③各自的功能(作用)是什么;二是①②③两两之间的关系是什么;三是借助求和符号所隐含的函数周期性如何通过①②③推演出来;四是①②③中“桥梁”是什么(②起着“桥梁”作用);五是f(x),g(x)之间的最简单的关系是什么(f(x)-g(x)=4);六是如何推导出函数g(x)的周期;七是在知道函数g(x)的一个周期为8时如何运用①②③去计算函数值．其三,对方程⑥的本质的理解既很重要,又有较高难度．其四,对数学关系的等价转化的深度理解.如把③等价变换成⑤,把f(2-x)-g(2-x)=4等价变换成f(x)-g(x)=4,等．其五,数学思想方法的灵活运用(迁移).如运用“消元法”时把某个“函数”当成一个“元”,当f(3)或g(3)不能单独计算出来时用整体思想去计算f(3)+f(7)或g(3)+g(7),等等．

3.2 指向多元表征的教学

深度教学是指向学生建构多元表征和牢固知识网络的教学．多元表征对深化数学知识理解、完善数学认知结构、丰富信息输出方式、创造新的数学对象组合等都具有重要作用．多元表征是用多种表示方法或形式来表达、理解数学概念、符号或问题．多元表征有符号表征、语言表征、图形表征、情境表征、操作表征等．如,f(-x)=f(x+6)有多种表征方法:其语言表征为“-x与x+6的函数值相等”或“复合函数f(-x)与复合函数f(x+6)是两个相同函数”;其图象语言表征为“f(x)的图象关于x=3对称”或“f(x)的图象的对称轴是x=3”;其符号表征有无穷个等价关系,也就是有f(x)=f(6-x)⟺f(x+3)=f(-x+3)⟺…．多元表征对理解数学概念、认识数学关系和建构知识网络都非常重要．多元表征在解决数学问题时可灵活选择并运用某些表征,有利于提高解题的针对性和效率．

指向多元表征的深度教学主要可从多元表征形式、多元表征顺序和表征组合方式三个方面入手．一是注意多元表征形式．由于多元表征形式的多样性,导致学生选择表征的多样性,这可能会增加学生选择合适表征形式的困难．选择合适(恰当)的表征形式,需要学生具有敏锐的观察、整体的预判和丰富的经验．二是注意多元表征的顺序．自然的解题思路一般具有内在逻辑关系,不同表征的出现顺序和应用顺序都会影响学生理解程度和解题思路．如,本试题已经知道两个函数方程①②,但“g(x+1)为奇函数”不是函数方程的形式,因此宜优先考虑把“g(x+1)为奇函数”转化成代数表征(函数方程)③,由此便可集中精力聚焦对函数方程①②③的探究．三是选择表征的组合方式．如,对函数方程①②③的探究有①②、②③、①②③的组合方式,探究发现②③组合较为简便．

3.3 指向知识迁移的教学

3.4 指向发现创新的教学

深度教学是指向学生在数学探究、数学建模和数学解题等活动中有新的拓展、新的发现即有所创新的教学．批判性思维作为创新的重要思维方法,有助于培养学生的创新意识、创新思维和创新能力[6]．数学解题时,在确保推理正确和运算准确的基础上,通过对解题思路的再批判、再思考、再修正,不断优化和创新解题方法,从而提升解题效率．本试题涉及的创新活动有解题方法创新、构造函数创新和编拟新问题创新等路径．一是当f(3)和f(7)、g(3)和g(7)都不能单独计算出来时,需要创新解题方法,即构造f(3)+f(7)或g(3)+g(7),并从整体上予以解决.二是当面对的两个函数f(x)、g(x)都高度抽象时,可结合题目条件和隐含条件构造一个特殊函数,如,本题可构造一个特殊函数:

由此可直接求出g(1),g(2),…,g(8)的函数值,类似的特殊函数可构造出无数多个,这有利于培养学生的发散思维.三是在弄清本试题本质的情况下,学生可编拟数学新问题,在教师的启发和指导下,学生通过思考、探究和讨论编拟出几个新的问题: