青菜高密度移栽机植苗机构的设计与试验

鲍李旭,俞高红,b,赵 雄,b,王 磊,b

(浙江理工大学,a.机械工程学院;b.浙江省种植装备技术重点实验室,杭州 310018)

0 引 言

目前,由于水土流失、荒漠化等原因,中国的可种植土地面积在不断减少。为了提高土地利用率,大多数的绿色蔬菜采取高密度种植[1],即行距和株距都小于150 mm,如青菜、鸡毛菜等[2]。这种高密度蔬菜种植主要依靠人工进行移栽[3],生产劳动强度大,效率低,密植移栽机是提升高密度种植效率的有效手段,但相关研究较少。

国外密植移栽机的研究主要集中在日本和韩国。如日本洋马公司的PF2R型两行自走式蔬菜移栽机[4],采用行星轮系-滑道式取苗机构以及鸭嘴式栽植机构,该机型栽植行距为450 mm左右,作业株距为260～800 mm,作业效率可达2500 株/(行·h),但其作业参数不能满足国内青菜密植移栽的要求。日本久保田公司的KP-201CR半自动两行自走式蔬菜移栽机[5],该机型的作业行距和株距范围分别为280～550 mm和220～800 mm,工作效率达1500株/(行·h),但其需要人工将秧苗喂入栽植吊杯,工作量大、效率低[6],同样不能满足国内密植移栽的要求。韩国的A5-1200型半自动密植移栽机[7],可以进行8行移栽作业,行距设定为150 mm,而株距可在100～500 mm范围内调整,然而其在作业时需要2名操作人员手动进行取苗和投苗,虽然在一定程度上减少了劳动力,但并未完全实现自动化;此外,该机器采用间歇式的移栽方式,工作效率相对较低,仅有600 株/(行·h)。目前国内蔬菜移栽机的植苗机构作业株距和行距都比较大,一般在300～500 mm,无法满足密植型蔬菜小株距小行距的栽植农艺要求[8]。植苗机构作为移栽机重要的工作部件[9],对移栽机的栽植效率以及栽植后的秧苗质量均有较大影响,因此为了满足密植型蔬菜小株距小行距的特定种植需求,设计一种与之相适应的多行同步植苗机构尤为关键。

近年来,国内针对植苗机构的研发工作也取得了一定的进展。黄前泽[10]、徐乐辉[11]提出了一种旋转式非圆齿轮行星轮系单行植苗机构,该机构植苗效率最高可达100 株/min,但其设计的非圆齿轮与栽植轨迹主要针对大株距的移栽场合。吴彦强等[12]针对山东地区辣椒密植需求,研制了自走式高密度辣椒移栽机,该机型可同时栽植6行钵苗,作业行距为300 mm,株距在160 mm左右,可满足青菜密植的株距、行距要求。汪应萍[13]针对青菜密植移栽的农艺要求,提出了一种史蒂芬森型六杆八行植苗机构,其理论移栽株距和行距都为110 mm,轨迹设计满足小株距移栽的农艺要求,但由于连杆机构在运动速度较高时振动较大,限制了该植苗机构的工作效率。

密植型蔬菜的经济价值高、产量需求大,国外尚无密植型全自动移栽机,已有的小型移栽机不适用于中国密植农艺要求。因此本文针对高密度、高效率两大设计要求,配合八行取苗机构进行青菜钵苗移栽作业,在非圆齿轮行星轮系八行取苗机构[14]的基础上提出了一种非圆齿轮行星轮系八行植苗机构,实现小株距与小行距多行移栽,以解决密植型蔬菜的机械化移栽的难题,促进密植型蔬菜钵苗机械化移栽的进程,提高农业生产的效率和质量,为密植移栽机的进一步研究提供技术支持和参考。

1 八行植苗机构的工作原理

针对密植型蔬菜小行距小株距、多行同步植苗的农艺要求,本文提出了一种非圆齿轮行星轮系八行植苗机构,机构示意图如图1所示。该机构主要分为两部分:传动部分和鸭嘴式栽植器部分。齿轮箱对称布置在机构左右两侧,两个齿轮箱之间等间距布置有16个栽植器(上下各8个),实现八行同步移栽。

1.太阳轮;2.中间轮I;2′.中间轮Ⅱ;3.行星轮;4.行星轮轴;5.行星架;6.凸轮;7.太阳轮轴;8.中间轮I;8′.中间轮Ⅱ;9.行星轮;10.左栽植嘴;11.左摆动臂;12.右摆动臂;13.右栽植嘴图1 八行植苗机构示意图

该机构的传动部分由7个非圆齿轮组成,中间轮8和8′、行星轮9分别是由中间轮2和2′、行星轮3绕太阳轮1啮合旋转180°得到。太阳轮1、中间齿轮2和2′、行星齿轮3和行星架5构成齿轮系传动,作业时太阳轮固定不动,行星架顺时针匀速转动[15],太阳轮1与中间轮2相互啮合传动,中间轮2′与中间轮2固定在一起,而中间轮2′与行星轮3相互啮合传动,使得行星轮作逆时针非匀速转动[16],栽植器通过行星轮轴4与行星轮3固连,通过两级非圆齿轮传动形成了植苗轨迹。

由于该植苗机构整体是左右对称的,以最左侧的齿轮箱和栽植器为例,对其余14个栽植器及另一侧齿轮箱进行简化处理。在旋转式传动箱体上下对称布置2个栽植器[17]。由于上下两个栽植器是相同的,因此本文以上栽植器为例对如何进行栽植作业作具体说明。栽植器机构简图如图2所示。固定板与行星轮轴固定在一起,而行星轮轴与行星轮也固定在一起,故行星轮会带动固定板一起作非匀速转动。左右摆动臂分别通过铰链与固定板连接,在固定板转动时,左摆动臂会与固连在行星架上的凸轮推程段发生碰撞,左摆动臂相对于固定板顺时针旋转一定角度,进而带动右摆动臂相对于固定板逆时针旋转一定角度。由于左右栽植嘴分别与左右摆动臂固定在一起,故左右栽植嘴也会随着左右摆动臂同时转动,此时形成了栽植器的张开状态,左摆动臂与凸轮的远休止段碰撞,使栽植器的张开状态持续一段时间。固定板继续转动,在拉簧的拉力作用下,左摆动臂与凸轮的回程段碰撞,左右栽植嘴迅速闭合。如此,行星架的周期性旋转使栽植器进入周期性的张开和闭合状态。

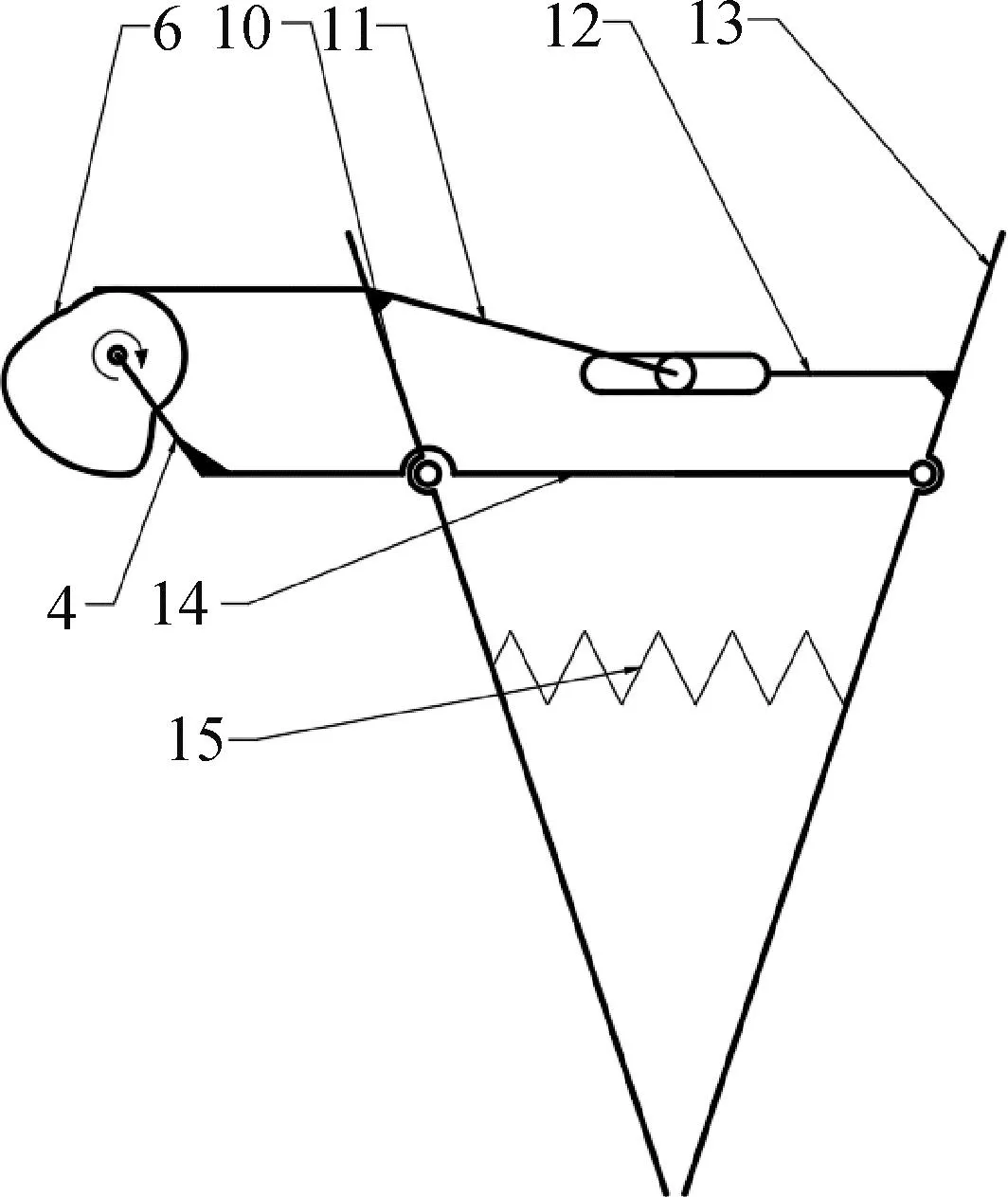
4.行星轮轴;6.凸轮;10.左栽植嘴;11.左摆动臂;12.右摆动臂;13.右栽植嘴;14.固定板;15.拉簧图2 栽植器机构简图(左视)

2 植苗机构运动学模型

运动学分析是优化设计的重要手段,以在满足运动要求的前提下优化机构参数,进而降低结构的复杂性[18]。由于八行植苗机构两侧完全对称,且一行8个栽植器运动轨迹完全一样,故在运动学建模时可只取一侧栽植器作分析。非圆齿轮可简化为节曲线的形式,非圆齿轮间的啮合旋转可简化为节曲线间的纯滚动,本文构建的植苗机构运动学模型如图3所示。以太阳轮旋转中心O点为坐标原点建立坐标系[19],对X轴下方的非圆齿轮及栽植器进行计算和求解,而上方的非圆齿轮及栽植器由前者绕太阳轮啮合旋转180°得到。首先分析行星轮系中各非圆齿轮之间存在的转角关系,并构建传动比函数;然后在齿轮啮合中心距给定的条件下计算出非圆齿轮的节曲线坐标,并推导出植苗机构栽植器尖点D的位移和速度方程;最后获得由栽植器尖点D周期运动形成的植苗轨迹。

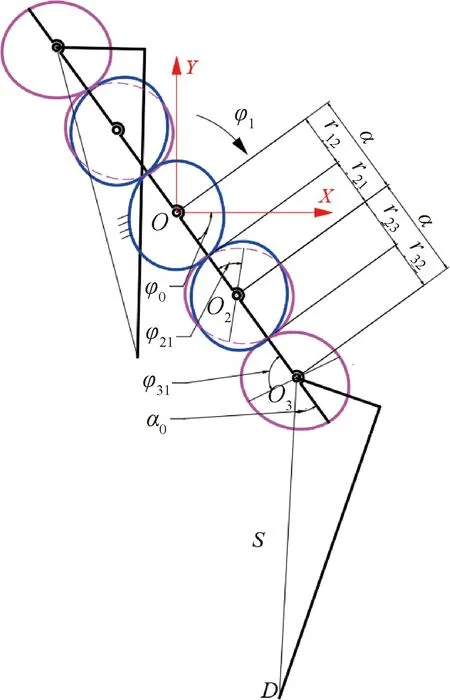
图3 植苗机构运动学模型

植苗机构运动学模型中的参数及其说明见表1。由于中间轮2和2′固连,它们在单位时间内产生的角位移相等,故在建立运动学模型时,为了简化建模过程,可以将中间轮2和2′先视作同一个非圆齿轮,在后续计算非圆齿轮节曲线坐标时再分开计算。

表1 植苗机构运动学模型参数说明

已知非圆齿轮节曲线是封闭的,即转角φ变化范围为φ∈[0,2π]。由于行星轮和中间轮的转角是在同一时间内完成的[20],即存在对应关系:φ31=f(φ21),当φ21=0时φ31=0,当φ21=2π时φ31=2π。根据上述转角关系,先设定行星轮与中间轮的转角函数关系为:

(1)

将φ21=0及φ21=2π分别代入式(1)中,验证

其满足上述设定的转角约束条件。

由式(1)可求得中间轮与行星轮的传动比函数:

(2)

其中:ω2为中间轮的自转角速度;ω3为行星轮的自转角速度。

由于太阳轮与中间轮,中间轮与行星轮之间的中心距是相等的,因此得到:

(3)

其中:φ23为中间轮相对于行星架的角位移;φ32为行星轮相对于行星架的角位移。

将式(3)代入式(2)中,可以得到:

(4)

由于太阳轮和行星轮对称分布在中间轮两侧,易知:

r21(φ21)=r23(φ21+π)

(5)

将式(4)代入式(5)中,可以得到:

(6)

由于太阳轮与中间轮的节曲线周长相等,则有:

(7)

当行星架转过dφ1时,中间轮转过dφ21,即r21(φ21)dφ21=r12(φ1)dφ1,则有:

(8)

将式(6)代入式(8),可以得到:

(9)

式(9)可改写为φ1=F(φ21),则:

(10)

将式(10)代入式(1)中,便得到了φ31与φ1的函数关系,由于自变量φ1是已知量,故中间轮的角位移φ21和行星轮的角位移φ31可以轻易求解。

在用数值法求解行星轮系总传动比时,可以将行星架旋转一周的转角单位化,取360等分,则有:

(11)

其中:ω1为行星架角速度(匀速),负号代表行星轮与行星架旋转方向相反。

为了便于求解各个非圆齿轮的节曲线,需要对中间轮2和中间轮2′分开求解。根据行星轮系转化原理,给太阳轮加上一个假想旋转,大小等于行星架转速ω1,方向与ω1相反,则行星轮系转化为定轴轮系[21]。在转化轮系中,行星轮与太阳轮的传动比在数值上等于原行星轮系中行星轮与行星架的传动比i31,中间轮2与太阳轮的传动比在数值上也等于原行星轮系中中间轮2与行星架的传动比i21:

(12)

则太阳轮与中间轮2啮合的向径分别为:

(13)

中间轮2′与行星轮的传动比:

(14)

则中间轮2′与行星轮啮合的向径分别为:

(15)

至此,已知非圆齿轮节曲线的向径和对应的转角,便可在极坐标系下绘出非圆齿轮的节曲线。

接下来建立栽植器尖点D的运动学方程,其中行星轮轴心的位移方程为:

(16)

栽植器尖点D的位移方程:

(17)

将式(16)和式(17)分别对时间t求导,可以得到行星轮轴心和栽植器尖点D的速度方程:

(18)

(19)

3 参数分析与优化

3.1 机构辅助分析与优化软件

栽植器轨迹的形状是影响植苗功能的主要因素[22]。根据上文建立的机构运动学模型可知,为获取一条符合青菜小株距移栽农艺要求的植苗轨迹及轨迹参数,需要对非圆齿轮行星轮系各机构参数进行调整。这是一个复杂的多目标多变量优化问题,每调整一次参数,都需要重新计算相关的数据,计算量庞大,而人机交互优化方式能较好解决该难题。本文基于Visual Basic 6.0编写了计算非圆齿轮节曲线的辅助分析与优化设计软件,为了便于用户和计算机之间的信息交互,搭建了如图4所示的用户界面(UI),UI可以为设计工作带来简便性和直观性。该软件的主界面包括菜单栏(区域1)、工具栏(区域2)、参数输入栏(区域3)、参数输出窗口(区域4)和图形显示窗口(区域5)等5个主要区域。

图4 植苗机构辅助分析与优化设计软件界面

在机构参数优化过程中,相关参数的调整在参数输入栏中进行,而一些重要参数值的输出,包括栽植器出土角和入土角等,则显示在输出窗口中。区域5是软件的主要显示和人机交互区域,通过调整区域3中的参数可以实时地将植苗机构的位置和运动状态显示在区域5中,包括栽植器尖点的相对运动轨迹(静轨迹)、绝对运动轨迹(动轨迹)和钵苗栽植位置等。此外,通过点击区域5中的任意两点可以测量出两点间的直线距离,便于设计者得到除区域4显示的参数以外的重要设计参数,包括轨迹高度、轨迹宽度、环扣高度、环扣宽度[23]等。机构水平前进速度可通过式(20)计算:

v=z·n·p

(20)

其中:v为机构水平前进速度,mm/s;z为行星轮系植苗机构旋转一周的栽植次数,r-1;n为机构转速,r/s;p为栽植株距,mm。

3.2 主要参数对种植轨迹的影响分析

为了满足小株距移栽(株距小于150 mm)的农艺要求,需要对轨迹的形状尺寸和栽植器的姿态设定约束条件[24],具体应满足以下5个优化目标:

a)栽植器的垂直平分线(对应着钵苗的姿态)在尖点D进入和离开土面时与土面(假设为水平面)的夹角应大于70°。

b)为了避免植苗机构在运行过程中与移栽机其他部位发生干涉,相对运动轨迹(静轨迹)宽度应小于200 mm,高度小于250 mm。

c)为避免栽植器植苗完成后,离开土面高度不够而夹住叶子带出钵苗,静轨迹的高度应大于200 mm。

d)栽植器尖点D的动轨迹需要存在一个细长形环扣,该环扣的高度要大于40 mm、宽度小于15 mm,以基本达到零速度栽植,并保证钵苗栽植后的直立度。

e)栽植机构尺寸不宜过大,否则在旋转过程中会发生干涉碰撞;但又不宜过小,否则会导致植苗深度不够。青菜钵苗的高度一般在120 mm左右,故栽植器的长度宜在160～200 mm之间。

通过该软件进行植苗机构的辅助分析和优化设计时,设计者需要在参数输入窗口内输入主要参数值,然后根据区域5中显示的植苗轨迹、参数输出栏中的重要参数值来调整输入的参数大小,以获得最佳的种植轨迹。为了便于调整这些参数以获得最佳结果,必须了解每个参数对种植轨迹的影响。因此,本文采用控制变量法来分析每个重要参数的改变会对植苗轨迹的形态和大小产生怎样的影响。

优化参数主要有:两相啮合非圆齿轮的中心距a,传动比系数k1、k2、k3,行星架初始安装角φ0,栽植器相对于行星架的初始安装角α0,中间轮相对于行星架的初始安装角γ0。

3.2.1 中心距a对植苗轨迹的影响

不同中心距a下的植苗机构相对运动和绝对运动轨迹如图5所示。通过只改变a可以看出,随着中心距a的增加,栽植器尖点D的相对运动轨迹逐渐变高变宽,而其绝对运动轨迹在最低端逐渐形成一个更小更深的环扣。

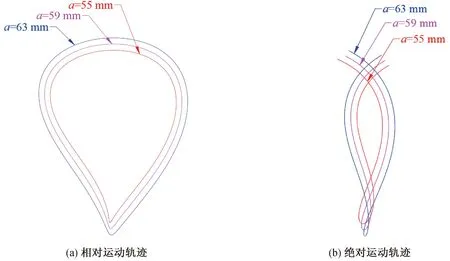
图5 中心距a的改变对植苗轨迹的影响示意图

3.2.2 传动比系数k1对植苗轨迹的影响

不同传动比系数k1下植苗机构的相对运动和绝对运动轨迹如图6所示。通过仅改变k1可以看出,随着传动比系数k1的增大,相对运动轨迹的高度保持不变,宽度逐渐变大;而绝对运动轨迹的环扣逐渐变小,这会影响栽植机构的零速度移栽,进而影响钵苗的直立度。k1的选取取决于静轨迹的宽度和动轨迹的环扣尺寸要求。

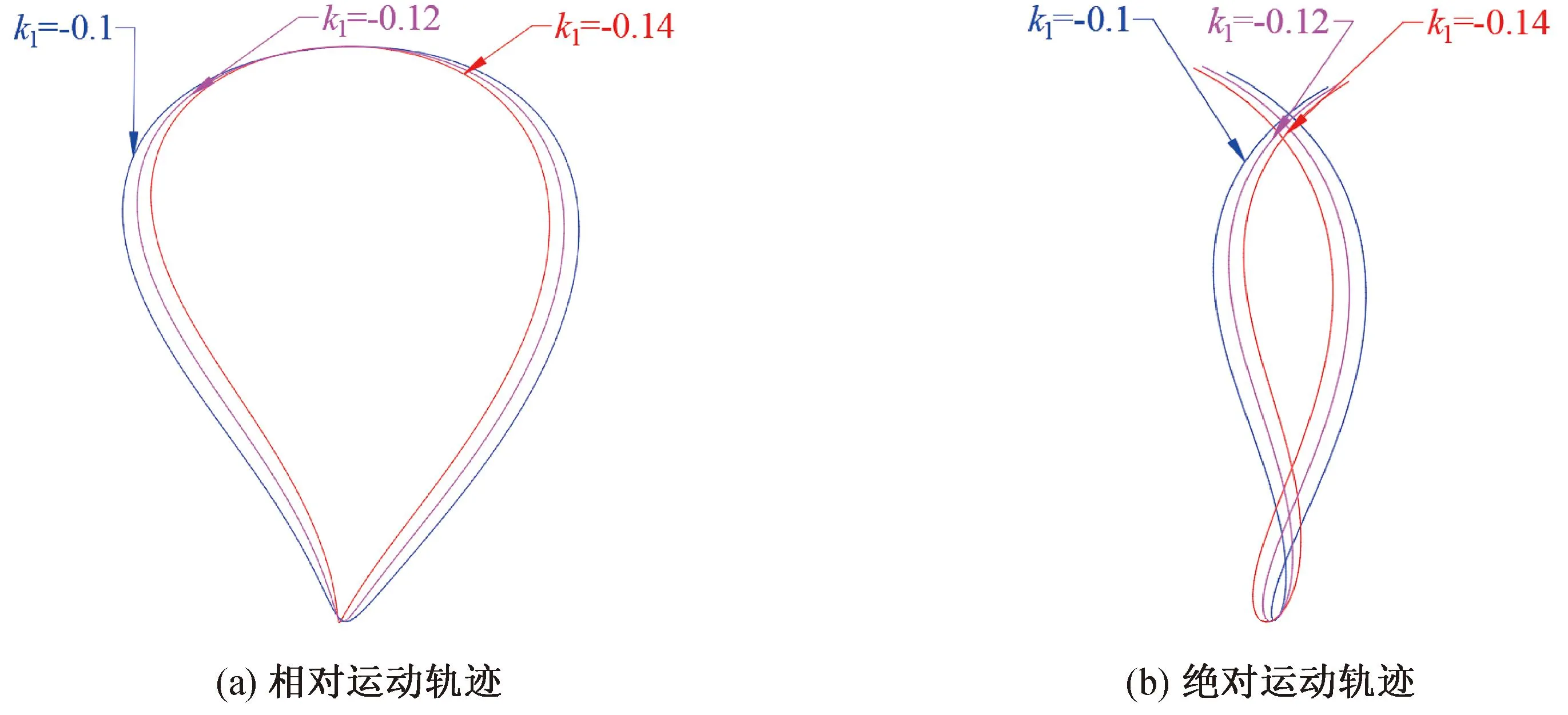
图6 传动比系数k1的改变对植苗轨迹的影响示意图

3.2.3 传动比系数k2对植苗轨迹的影响

不同传动比系数k2下植苗机构的相对运动和绝对运动轨迹如图7所示。通过仅改变k2可以看出,随着传动比系数k2的增大,相对运动轨迹的顶部变宽,而其底部变窄,同时轨迹高度保持不变;而在绝对运动轨迹上,底部环扣逐渐变宽变高,环扣过大会导致钵苗的直立度变差。k2的选取同样取决于静轨迹的宽度和动轨迹的环扣尺寸要求。

图7 传动比系数k2的改变对植苗轨迹的影响示意图

3.2.4 传动比系数k3对植苗轨迹的影响

不同传动比系数k3下植苗机构的相对运动和绝对运动轨迹如图8所示。通过仅改变k3可以看出,随着传动比系数k3的增大,相对运动轨迹底部变宽,上端变窄,轨迹高度保持不变;绝对运动轨迹环扣宽度明显变小,环扣高度变小。k3的选取取决于栽植直立度和动轨迹的环扣尺寸要求。

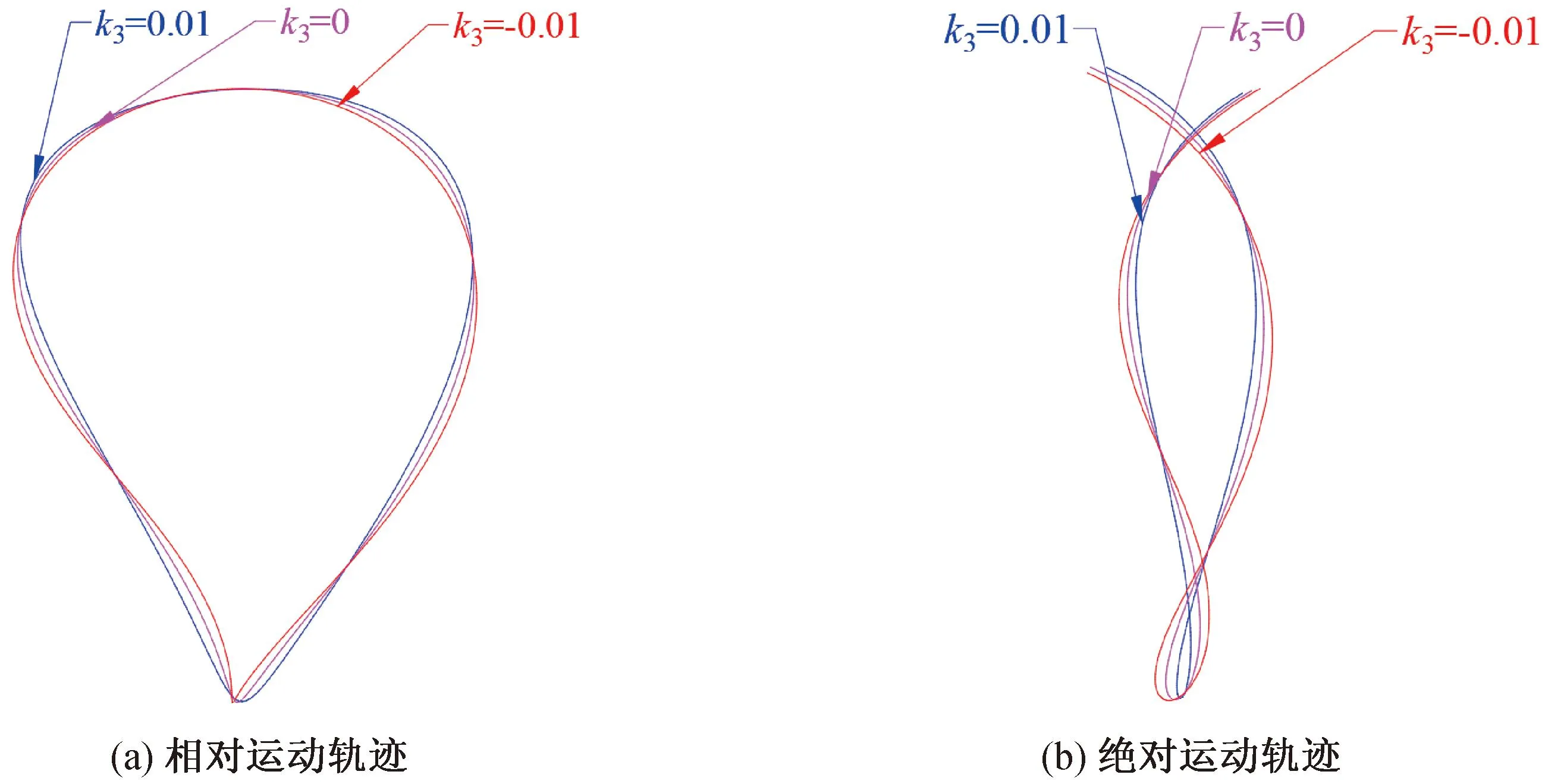
图8 传动比系数k3的改变对植苗轨迹的影响示意图

3.2.5 行星架初始安装角φ0对植苗轨迹的影响

不同初始安装角φ0下植苗机构的相对运动和绝对运动轨迹如图9所示。通过仅改变φ0可以注意到,随着初始安装角φ0的增加,相对运动轨迹和绝对运动轨迹的形状和大小没有改变,轨迹整体向右上方旋转。为了保证植苗机构在轨迹上端(接苗阶段)运动时的平稳性,相对运动轨迹上端应尽量水平。φ0的选取取决于栽植器接苗时的垂直度和栽植直立度要求。α0和γ0的选取依据与φ0基本类似。

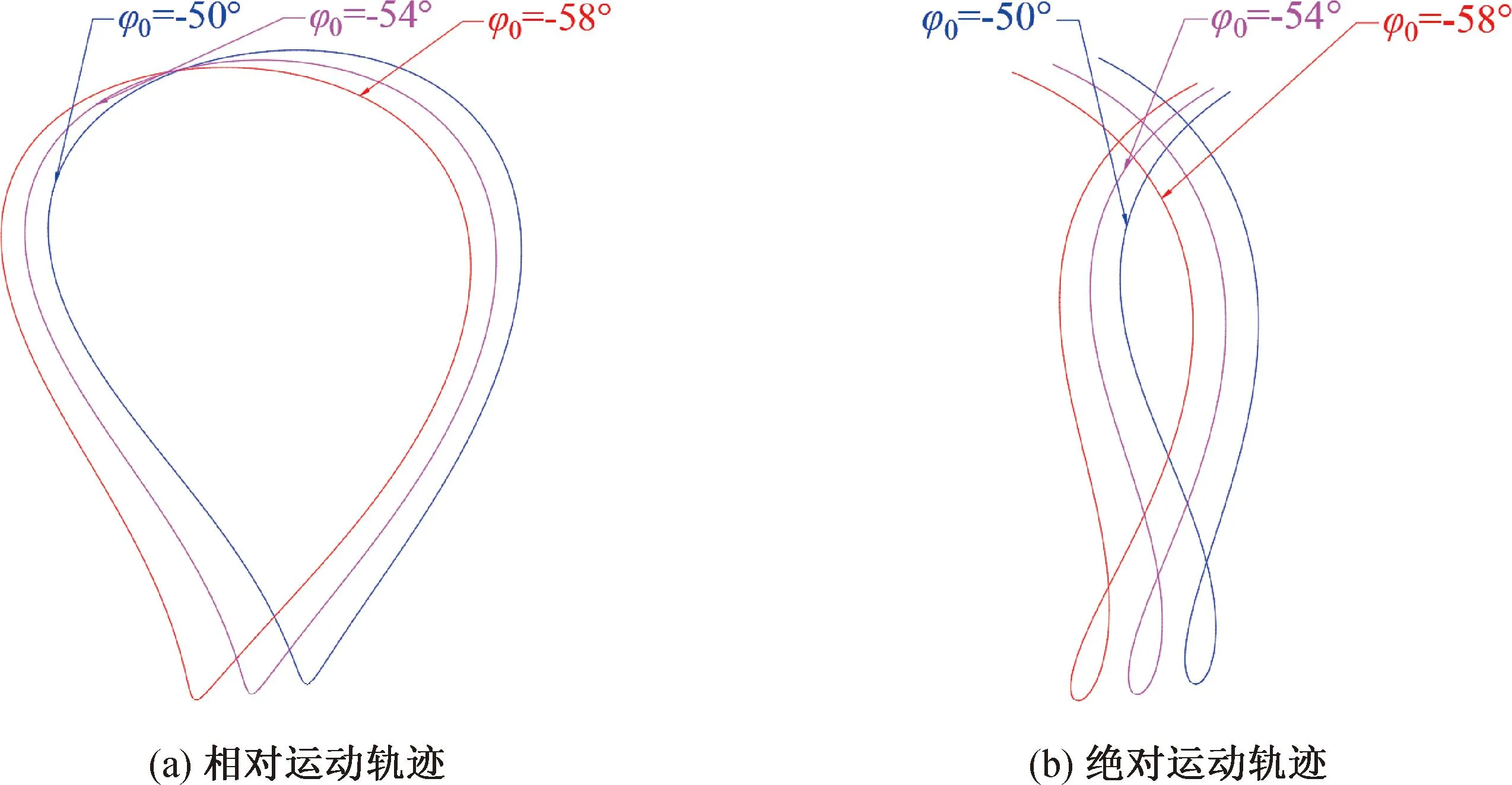
图9 行星架初始安装角φ0的改变对植苗轨迹的影响示意图

根据前面的分析,行星齿轮系的中心距a主要影响轨迹的大小,从而影响植苗机构的总体尺寸。行星架初始安装角φ0、栽植器相对于行星架的初始安装角α0和中间轮相对于行星架的初始安装角γ0主要影响轨迹整体的角度,它们对植苗轨迹的大小影响微乎其微。传动比系数k1、k2和k3对绝对运动轨迹最低端的环扣形状和尺寸影响最大。

3.3 植苗机构参数优化步骤与结果

为了得到符合前文提出的若干优化目标的植苗轨迹,参数优化过程如下:

a)预先人为给定一组各参数初始值,同时也会获得对应的植苗轨迹和一组优化目标值。

b)通过上述分析明确了各参数变化对植苗轨迹的影响规律,通过人机交互的方式不断针对性改变上述各参数值大小,直到植苗轨迹和其对应的优化目标值逐步符合要求。

依据上述步骤,最终得到一组较优的机构参数:a=59 mm,k1=-0.12,k2=0.07,k3=0,φ0=-54°,α0=-164°,γ0=142°,S=185 mm。此时,栽植器插入垄面的深度为60 mm,对应于前文优化目标的优化结果如表2所示,相关数据在轨迹中测量的位置如图10所示。

表2 指标的优化结果与设计目标的对比

1.相对运动轨迹;2.绝对运动轨迹图10 理论植苗轨迹及优化结果示意图

4 八行植苗机构结构设计与仿真

4.1 整体结构设计

非圆齿轮行星轮系八行同步植苗机构的三维模型如图11所示,该机构由两套对称布置的行星轮系齿轮箱和上下布置的16个栽植器部件组成。在植苗机构旋转运动过程中,由于16个栽植器通过L型横杆固连,故植苗轨迹完全相同。该八行植苗机构设定的理论株距为110 mm,横向连续布置的8个栽植器的间距为110 mm,故理论行距也为110 mm。

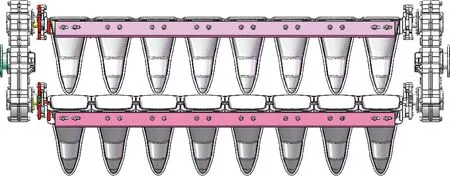
图11 八行植苗机构三维模型

4.2 植苗机构仿真分析

基于SolidWorks Motion模块对建立好的植苗机构(单边)进行运动学仿真分析,得到栽植器尖点的相对运动轨迹仿真结果,如图12(a)所示;并将其与辅助分析与优化设计软件中的理论轨迹作对比[25],如图12(b)所示,仿真轨迹与理论轨迹基本重合,对比情况验证了三维模型设计的正确性。

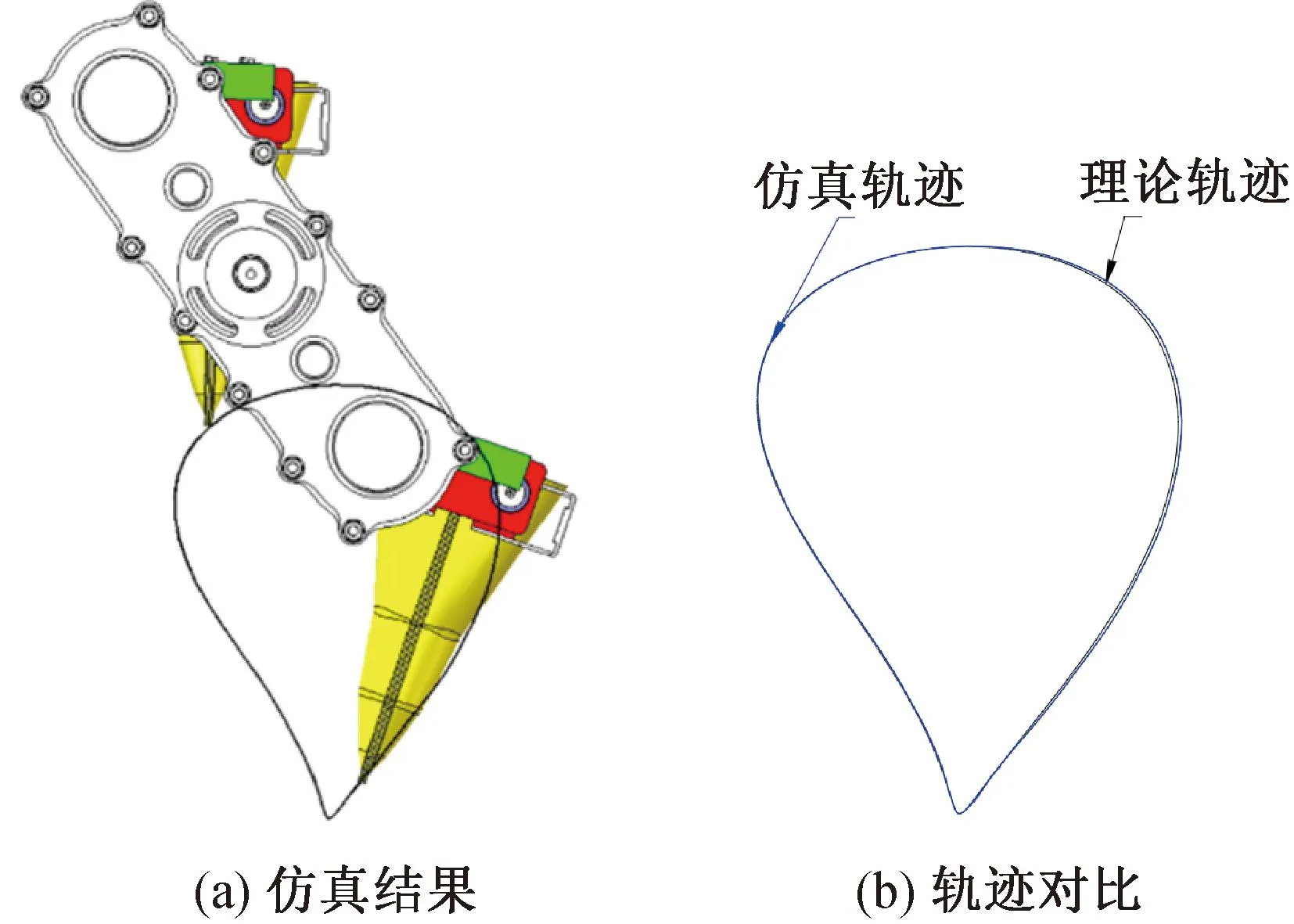
图12 仿真结果与轨迹对比示意图

除了将仿真轨迹的形状与理论轨迹做对比外,还需要验证本文提出的若干优化目标值。优化目标值在仿真轨迹中的示意图如图13所示,齿轮箱以连杆形式表示,垄面设定在轨迹最底端上方60 mm处。仿真结果与理论优化值对比情况如表3所示,可以看出,同一优化指标下的仿真值和理论值基本一致,进一步验证了三维设计的正确性。

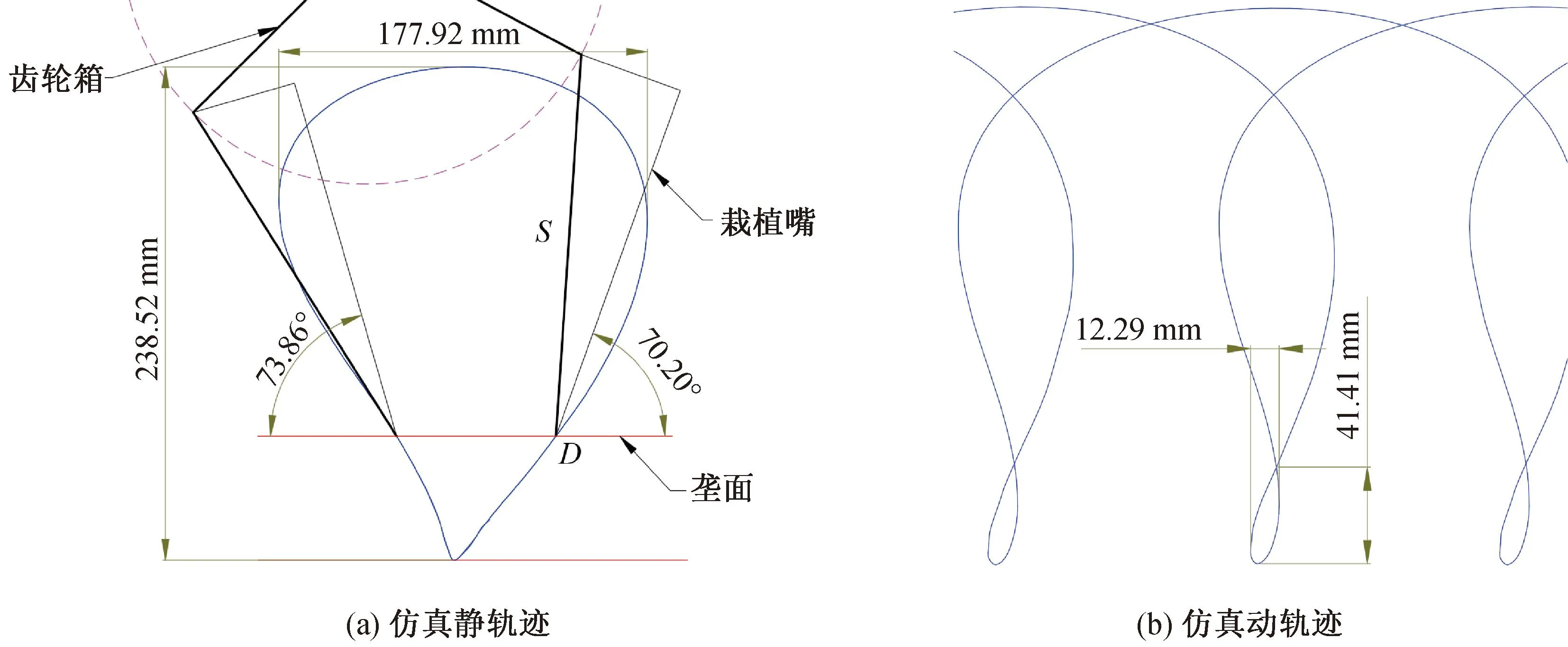
图13 优化目标值在仿真轨迹中的示意图

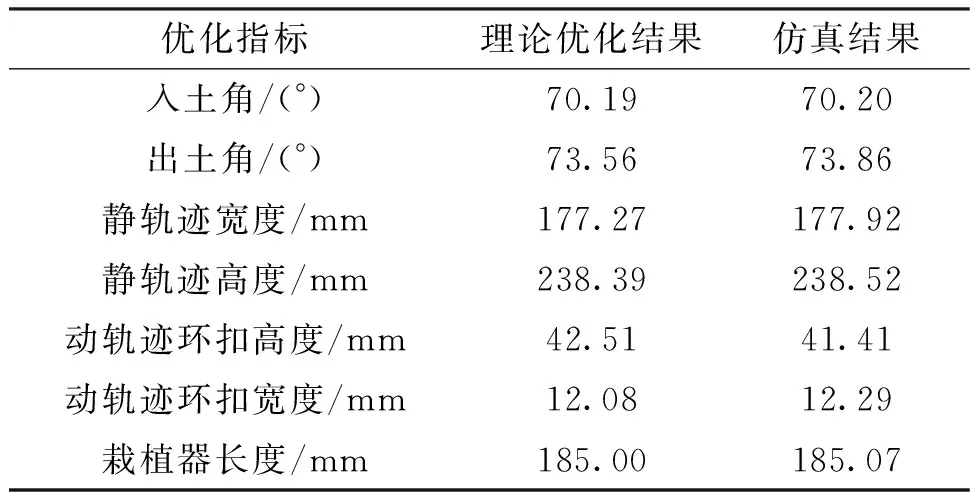
表3 优化目标值的理论优化结果和与仿真结果

利用SolidWorks Motion模块的速度分析功能导出栽植器下端尖点D一个周期内的水平和竖直方向的速度变化数据,并在Origin中绘制仿真速度曲线和理论速度曲线进行对比如图14所示。由于零件间存在碰撞,所以曲线存在锯齿状波动,但不会影响整体变化趋势,仿真速度曲线与理论速度曲线基本重合,进一步验证了三维模型设计的正确性。仿真设定的机架转速为20 r/min,水平方向速度曲线在0.3 s左右时存在速度接近0 mm/s的时刻,对应的竖直方向速度曲线在0.3 s左右时存在速度为0 mm/s的时刻,此时栽植器正在执行植苗动作,可以实现接近零速度植苗。

图14 尖点D仿真速度曲线和理论速度曲线对比示意图

5 八行植苗机构的试验

为了进一步验证八行植苗机构理论计算模型的正确性以及运用到实际工作的可靠性,将实物样机装配在自主设计的青菜高密度八行自动移栽机上进行田间试验,八行植苗机构实物样机如图15中矩形框内所示,青菜高密度自动移栽机整体如图16所示。

图16 青菜高密度移栽机实物样机照片

试验场地垄面宽110 cm,垄高15 cm;试验选用培育时间为30 d的青菜苗,苗株高8～15 cm,真叶数3～5片,散坨率小于5%(钵苗的盘根效果会直接影响取苗效果)。植苗机构田间试验如图17所示,株距测量结果如图18所示,相邻青菜苗的距离约为110 mm,与理论设计株距一致,验证了实物样机搭建的正确性。

图17 田间试验移栽作业照片

试验中取苗机构转速设置为15 r/min,由于取苗机构旋转一周可取苗16株,八行植苗机构旋转一周可以栽植钵苗16株,故对应的植苗机构转速也设置为15 r/min,移栽机前进速度为55 mm/s,移栽株距和行距均为110 mm,故移栽效率为240株/min。移栽过程中,出现漏栽、倒伏、埋苗[26]均记为移栽失败。试验结束后,根据记录的钵苗总数以及移栽成功数,可以计算出移栽成功率。由于钵苗移栽需要经过取苗、植苗两个阶段,故移栽成功率实际上与取苗成功率、植苗成功率存在一定关系,而本文主要研究对象为植苗机构,故应由植苗成功率而非移栽成功率来反映机构的实用性,所以还需要记录取苗成功率。为了忽略取苗失败的影响,假设取苗成功率可以达到100%。本文植苗成功率由式(21)计算得出:

(21)

其中:σz为植苗成功率;σy为移栽成功率;σq为取苗成功率。

移栽试验结果数据如表4所示,经过10次移栽试验,平均植苗成功率达到93.9%。在取苗成功率假设为100%的前提下,植苗成功率未达到100%的主要原因在于取苗成功之后还存在推苗过程。在该过程中,如果钵苗没有以较好的姿态落入栽植嘴中,会直接影响植苗效果,导致移栽失败。

综上所述,移栽失败的原因主要有:a)漏栽。取苗机构在推苗阶段未能成功将钵苗推入栽植器中,存在钵苗叶子挂在取苗机构上的情况。b)倒伏。在取苗机构推苗后,钵苗由于与导苗杯存在碰撞,影响了钵苗下落的姿态,使其落入栽植器时钵苗基质不再朝下。c)埋苗。垄面高低不平,部分钵苗栽植过深时会被覆土机构的覆土过程掩埋。

青菜密植移栽照片如图19所示,移栽密度超过70株/m2,从图中可以看出,除去个别漏栽、倒伏、埋苗的情况,整体效果满足青菜移栽农艺要求,表明该非圆齿轮行星轮系八行植苗机构具备可行性及实用性。

图19 青菜钵苗移栽照片

6 结 论

本文为实现青菜钵苗的机械化高效移栽作业,基于青菜钵苗移栽的株距行距农艺要求,提出了一种旋转式非圆齿轮行星轮系八行植苗机构。通过开展非圆齿轮行星轮系的运动学建模与分析、参数优化、植苗机构的虚拟样机仿真和田间试验等研究工作,得到的主要结论如下:

a)借助编写的植苗机构辅助分析与优化设计软件,通过人机交互的方式获得了一组最优的机构参数,此时设计株距为110 mm,满足青菜移栽的小株距要求。通过横向连续布置八个栽植器实现八行同步植苗,此时设计行距为110 mm,满足青菜移栽的小行距要求。

b)开展了植苗机构三维模型的虚拟样机仿真,并将仿真轨迹和理论轨迹进行了对比,验证了植苗机构设计的正确性。

c)进行了实物样机的田间移栽试验,在作业转速为15 r/min、前进速度为55 mm/s的情况下,平均植苗成功率达到了93.9%,移栽密度超过70株/m2,满足青菜小株距小行距移栽的农艺要求,验证了该植苗机构的实用性。

本文为蔬菜钵苗密植移栽机植苗机构的研发提供了理论和试验依据,从而推动密植型蔬菜机械化移栽的进程。