真空吸入式风洞三维非定常流场时空特性

刘艳欣,朱乐乐,陆文斌,钱海玥,刘 越

(1.上海航天电子技术研究所,上海 201108;2.郑州飞机装备有限责任公司,河南 郑州 450005)

0 引言

目前,悬挂发射装置常规的地面模拟投放试验是在标准大气条件下进行的,忽略了气动载荷对分离参数的影响,但随着新一代战机对高空、高速环境的要求日益苛刻,这就要求在进行地面投放试验时应尽可能地模拟真实的力学环境。针对上述悬挂发射装置空气动力学问题,提出了飞行载荷模拟系统,即根据流体力学的流动相似理论,对悬挂发射装置施加空气动力,以模拟其在空中挂飞或投放瞬间的气动载荷,同时实现分离参数的测试。该系统可以模拟悬挂发射装置在高空飞行状态下的气动环境,可以提高分离参数的置信度,为悬挂发射装置的研制提供可靠的试验数据。因此开展飞行载荷模拟系统研究具有重要意义。

一般而言,悬挂发射装置在空中挂飞和投放瞬间的气流速度在0.40～0.80Ma范围内。由于飞行载荷模拟系统与风洞有着相似的原理和结构,所以该系统属于高亚音速风洞,而高亚音速风洞的本质与低速风洞相似。目前,诸多学者对低速风洞的研究聚焦在直流暂冲式风洞和连续回流式风洞。文献[1]针对F-22 V-9模型,采用流体力学对其进行了数值模拟,并通过低速风洞试验研究了垂直尾翼的抖振现象。文献[2—3]针对连续式回流风洞,建立了全尺寸三维计算域,采用流体力学数值模拟方法研究了气流速度、压力等参数,并评估了试验段的流场品质。文献[4]针对亚音速风洞的收缩段,采用流体力学数值模拟方法研究了流场的均匀性、湍流强度和边界层。文献[5]针对低速风洞通过试验和理论分析研究了双三次曲线的速度分布和压力分布特性。文献[6]针对低速风洞的收缩段,研究了其收缩比、速度场和压力场。文献[7]针对回流式低速风洞研究了其收缩段的流场特性。文献[8]针对低速回流式风洞构建了收缩段的几何模型,并采用流体力学算法进行了数值模拟。文献[9]针对低速直流式风洞,试验研究了风洞的速度场和湍流强度。文献[10]针对直流式低速风洞,建立了非定常流动的数学模型,研究了试验段的气动布局。文献[11]研究了低速风洞收缩段的流场特性,并设计了收缩段。文献[12]针对0.3 m×0.3 m低速回流式风洞建立了数学模型,并进行了试验对比研究。文献[13]针对低速连续回流式风洞研究了风扇不同安装角度对流场特性的影响。由此可以看出,低速风洞流体运动的动力主要来源于风扇运动时所产生的压差。文献[14]所研究的飞机驾驶舱等熵、等温减压过程的动力源于高压室与低压室所产生的压差。本文所提出的飞行载荷模拟系统的气动布局既根据低速风洞的结构特点,又结合高低压室气体流动原理设计而成,也即真空罐吸入原理。

本文针对悬挂发射装置空气动力学问题,通过建立收缩段和真空罐的数学模型,确定其特征参数;应用空气动力学知识,抽象流体的边界条件,构建全尺寸三维流体计算域;采用流体力学数值模拟方法,利用试验验证算法的置信度,采用有限元体积法求解雷诺时均方程(RANS),研究三维非定常流场的时空特性及其演化规律。

1 真空吸入式风洞原理

悬挂发射装置在空中的投放时间较短,因此风洞试验段的流场不需要维持较长时间。基于此,本文采用真空吸入式风洞。该风洞主要由收缩段、试验段、扩散段、真空罐和爆破门组成,且收缩段、试验段和扩散段构成拉瓦尔喷管,物理模型如图1所示。收缩段可以将流体的压能转化为动能,增大速度;试验段用于飞行载荷模拟试验;扩散段可以将流体的动能转换为压能,减小流体能量损失;爆破门用于控制流体流动;真空罐用于产生负压,即利用前室的压力大于负压罐的压力,使流体流动。

图1 真空吸入式风洞物理模型Fig.1 Physical model of a vaccum suction wind tunnel

在试验前,风洞的爆破门处于关闭状态;在进行试验时使用真空泵将真空罐内的空气尽可能抽至真空,然后在外力的驱动下打开爆破门,空气在收缩段加速至亚音速后,由试验段进入扩散段,扩散段将动能转化为压能,然后由爆破门进入真空罐,当真空罐内的压力达到一定值时,在试验段形成稳定的流场,并且持续一段时间,最后随着空气不断被吸入真空罐,试验段的流场遭到破坏,试验随之结束。

2 真空吸入式风洞流场数值模拟

2.1 流体计算域构建

2.1.1真空罐特征参数确定

基于真空罐吸入原理,假设气体在真空吸入式风洞中的流动过程为绝热流动,且忽略气体沿近壁面流动,以及爆破门开门过程因摩擦而损失的能量,即气体在流道中的流动是可逆的。因此,真空吸入式风洞气体的流动过程可简化为一元可压缩气体的等熵流动过程。图2给出了真空吸入式风洞一元可压缩气体等熵流动示意图。

图2 一元可压缩气体等熵流动示意图Fig.2 Unidirectional compressible gas isentropic flow

基于上述假设,并结合空气动力学知识[15-16],可得不同海拔高度和马赫数下的质量流量为

(1)

式中:对于20 ℃的空气而言,k为绝热指数,取值为1.4;R为常数,取值为287 J/(kg·K);T0为总温,取值为293 K;p0为总压;A为试验段截面积,本文取4.4 m2。

基于真空罐吸入原理,假设真空罐的初始真空度为pei,罐内空气质量为Mei,试验结束时的真空度为pef,罐内空气质量为Mef,真空罐的体积为V,试验结束时真空罐温度为Tef。因此,真空罐内流体质量的变化量为

(2)

结合式(1)和式(2),真空吸入式风洞试验时间的表达式为

(3)

假设真空罐的的初始真空度pei=0;试验结束时,真空罐的压力为试验段的压力pef=p,温度为试验段流体的温度Tef=T。结合一元可压缩气体等熵流动滞止关系式[14],式(3)可简化为

(4)

式(4)即为真空罐容积表达式。

将k=1.4,T0=293,A=4.4,R=287代入真空罐容积数学模型中,解算得到了真空吸入式风洞在不同马赫数下的流场物理量值,如表1所列。

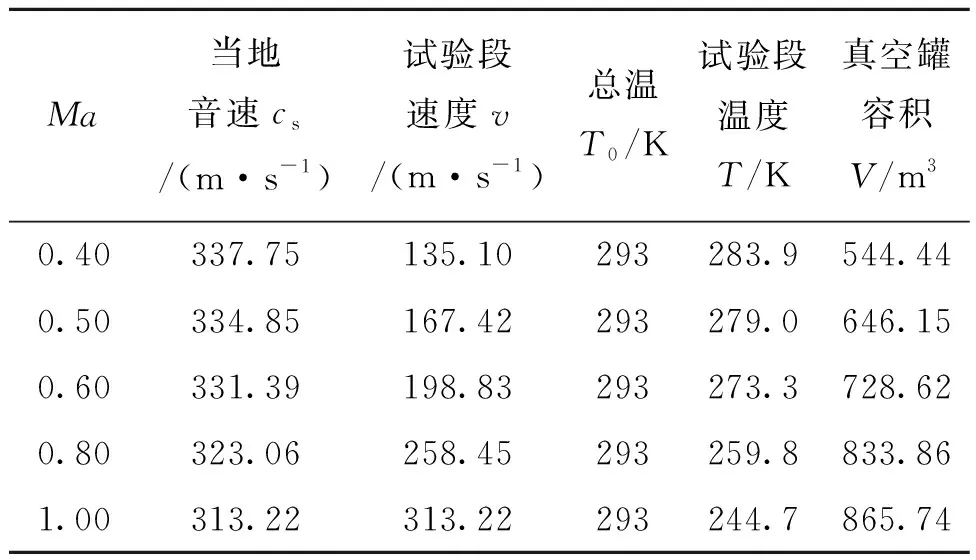
表1 真空吸入式风洞不同马赫数下的流场参量值Tab.1 Flow field parametric values at different Mach numbers in vacuum suction wind tunnels

假设气动载荷模拟的试验时间为1 s,马赫数为0.80,由表1可知真空罐容积为833.86 m3。考虑到真空罐的真空度不能抽至绝对真空,以及爆破门开启过程中的能量损失,真空罐容积拟设计为2 000 m3,真空度设计为3 000 Pa。

2.1.2其他特征参数确定

真空吸入式风洞的试验段上端面宽2.0 m,高2.2 m,且与轴向成0.5°的扩散角;两扇爆破门宽1.4 m,高2.2 m;真空罐直径14 m,高14.9 m;收缩段上端面宽8.6 m,高8.6 m且收缩段宽度方向和高度方向收缩比分别为16.81和3.91。以收缩段上端面中心为坐标原点,以横轴为x轴,以纵轴为y轴,z轴由右手定则确定,建立三维直角坐标系。收缩段为五次幂收缩曲线,其宽度方向方程式为[17]

(5)

式中:η1为宽度方向的收缩比,L为试验段长度,h0为试验段宽度。

收缩段高度方向的五次幂方程式为

(6)

式中:η2为高度方向的收缩比,h1为试验段高度。

2.1.3流体域网格及边界条件

真空吸入式风洞网格采用四面体非结构化网格,鉴于爆破门的流体流动梯度较大,以及为了更为精确地捕捉试验段流场的流动细节,对爆破门和试验段的网格进行了加密处理,经网格无关性验证,数值模拟所用网格数量控制在600万范围内。真空吸入式风洞采用真空罐吸入原理,试验段气源为空气,绝对总压为101 325 Pa,总温为293 K,雷诺数表达式为[18]

(7)

式中:v为流速,μ为动力粘度系数;D为水力直径,其表达式为

在临床上，冠心病患者容易发生充血性心力衰竭，而冠心病合并心衰后，患者的心肌会发生缺血、坏死等一系列的恶性改变，会导致心功能严重下降[1]。目前心肌能量代谢相关药物对冠心病心衰合并糖尿病患者有良好的治疗效果。该研究选取了曲美他嗪来治疗冠心病心衰糖尿病患者，并选取该院在2016年1月—2018年1月期间收治的140例冠心病心衰合并糖尿病患者为研究对象，观察曲美他嗪在治疗冠心病心衰合并糖尿病的临床治疗效果，现报道如下。

(8)

由式(7)和式(8)可知,流体的雷诺数为8.75×107,该值远大于2 200,由此可知该系统的流场为湍流。流体的水力直径为2.1 m、湍流强度为1.6%,因此收缩段上端面采用压力进口;根据理论分析,真空罐真空度为3 000 Pa,温度为293 K;收缩段、试验段、扩散段和真空罐表面为壁面;爆破门和真空罐之间采用interface进行数据传递。图3给出了真空吸入式风洞数值模拟网格模型与边界条件。

图3 真空吸入式风洞数值模拟网格模型与边界条件Fig.3 Numerical simulation grid model and boundary conditions in avacuum sunction wind tunnel

2.2 数值算法

基于流体质量守恒定律,在笛卡尔坐标系下的三维Navier-Stocks(N-S)方程守恒形式的基本控制方程为

(9)

式中:W为所求解的守恒变量向量;F和G为W的函数,分别描述对流与扩散过程;S为源项。本文采用ANSYS Fluent 2020R2软件对真空吸入式风洞的流场进行模拟。选用有限元体积法求解雷诺时均方程(RANS),选择密度基作为其求解器,并采用非定常法捕捉流场的演化过程;选取k-εRealizable两方程模拟湍流模型,采用标准壁面函数对近壁面的流动进行简化,并使用能量方程;假设气体服从理想气体状态方程,并采用无滑移壁面模拟收缩段、试验段、扩散段、真空罐和爆破门的壁面;采用全隐式的时间推进格式,对于k-ε方程选择一阶上迎风格式进行离散,并选用混合模式对流场进行初始化[19-20]。

2.3 数值算法验证

为验证所用计算网格与数值算法的准确性,采用文献[21]所述的模型进行算例验证。图4给出了真空吸入式风洞数值模拟算法验证所需模型及其减压舱压力平衡曲线。图中P0dec为减压舱初始压力,P0vac为真空罐初始压力,Pbal为平衡时的压力。

图4 数值模拟算法验证所需模型及其减压舱压力平衡曲线Fig.4 Numerical simulation algorithm to verify the required model and the pressure balance curve of the decompression chamber

由图4可知,通过数值模拟所得减压舱的气体达到动态平衡时所需时间在111～130 ms范围内,而文献[21]通过数值模拟和试验所得平衡时间分别约为112 ms和127 ms。因此,可以认为本文所述网格与数值算法置信度较高,可以进一步开展真空吸入式风洞流场特性的研究工作。

3 真空吸入式风洞内流场时空特性及其演化规律

为了得到三维非定常流动的真空吸入式风洞的流场品质,采用计算流体动力学(CFD)算法进行数值模拟。从收缩段出口开始沿着流场的速度方向每间隔2.1 m取一个截面,共取6个截面,即x=6.07,8.17,10.27,12.37,14.47,16.57 m,分别为A,B,C,D,E,F截面,研究每个截面速度场、压力场、俯仰角和偏航角的时空特性。

3.1 试验段速度场的时空特性及其演化规律

图5(a)和(b)给出了真空吸入式风洞试验段每个截面的几何中心在0～2 s范围内速度场的时空特性。图中Ts和Tf分别为试验段流场建立的起始时刻和结束时刻。图5(c)给出了不同时刻每个截面的速度云图。图中速度场1为A,B,C,D,E,F截面不同时刻的马赫数分布云图,速度场2为z=0截面不同时刻的马赫数分布云图。

图5 试验段速度场的时空特性Fig.5 Spatiotemporal characteristics of velocity field in test section

由图5(a)可知,真空吸入式风洞试验段流体的流动时间在0～2 s范围内,马赫数先增大至约0.95(0.23 s),然后减小至约0.80(0.35 s),流场在此马赫数下持续约1 s后,从1.37 s开始不断减小。由此可知,流场在刚开始阶段存在过冲现象,但又迅速达到平衡。因此,试验段可以提供马赫数约为0.80,且持续时间约为1 s的流场,可以满足流场马赫数为0.40～0.80,且持续时间为500 ms的设计要求。

从图5(c)流场的演化过程可知,试验段在建立稳定的流场后,每个截面处的马赫数分布比较均匀,不存在激波结构,且边界层厚度较小。为减小边界层厚度所导致的试验段可能出现的逆压梯度对流场品质带来的影响,试验段存在0.5°的扩散角,并与收缩段连接,构成了拉瓦尔喷管。流体经过收缩段加速后,在试验段入口马赫数达到0.95,根据拉瓦尔喷管原理,一维定常等熵流动的气体的流速只有在收缩段被加速至音速时,试验段才会出现超音速,进而可能存在激波结构;反之,流体经过试验段时速度会有所减小。因此,真空吸入式风洞试验段不会出现激波结构,其流场品质不会受到激波结构的干扰。

3.2 试验段压力场的时空特性及其演化规律

图6(a)和(b)给出了每个截面的几何中心处在0～2 s范围内静压的时空特性。图6(c)给出了不同时刻每个截面的静压云图。图中静压场1为A,B,C,D,E,F截面在不同时刻的静压分布云图,静压场2为z=0截面不同时刻的静压分布云图。

图6 试验段静压场的时空特性Fig.6 Spatiotemporal characteristics of static pressure field in test section

由图6(a)可知,真空吸入式风洞试验段流体的流动时间在0～2 s范围内,静压先减小至约40 kPa(0.23 s),然后增大至约69 kPa(0.35 s),流场在此压力下持续约1 s后,随着空气不断地吸入,流场平衡态遭到破坏,静压从1.37 s开始不断增大。由图6(b)可知,流场在0.35 s和1.37 s时沿轴向的静压略有增大,在66～69 kPa范围内波动,存在较小的逆压梯度。从图6(c)流场的演化过程可知,试验段在建立稳定的流场后,每个截面处的静压力分布比较均匀,且边界层厚度较小;当流动时间大于1.37 s后,静压在轴向出现了较大的压力梯度。

真空吸入式风洞试验段存在0.5°的扩散角,并与收缩段连接,构成了拉瓦尔喷管。根据拉瓦尔喷管原理和伯努利方程可知,当亚音速流体经过拉瓦尔喷管的收缩段时,流体流速增大,将压能转化为了动能,压力减小,流场的均匀性得到了提高;然后,流体经过试验段时,流速有所减小,又将部分动能转化为了压能,压力沿轴向略有增大,使其存在较小的逆压梯度,因此,会出现上述现象。

图7(a)和(b)给出了每个截面的几何中心处在0～2 s范围内总压的时空特性。图7(c)给出了不同时刻每个截面的总压云图。图中总压场1为A,B,C,D,E,F截面在不同时刻的总压分布云图,静压场2为z=0截面不同时刻的静压分布云图。

图7 试验段总压场的时空特性Fig.7 Spatiotemporal characteristics of total pressure field in test section

由图7(a)可知,真空吸入式风洞的流体流动时间在0～2 s范围内,总压先减小至约60 kPa(0.23 s),然后增大至约100 kPa(0.35 s),流场在此压力下持续约1 s后,随着空气不断地吸入,流场平衡态遭到破坏,总压从1.37 s开始不断增大,超过了初始压强。试验段在平衡阶段的总压小于初始压强,主要是高马赫数下流体的可压缩性变大使其密度减小所致。由图7(b)可知,流场在0.35 s和1.37 s时沿轴向的总压略有增大,在96～98 kPa范围内波动,存在较小的逆压梯度。这主要因为在流体达到平衡阶段时,动压沿轴向减小,静压沿轴向增大。从图7(c)流场的演化过程可知,试验段在建立稳定的流场后,每个截面处的总压力分布比较均匀,且边界层厚度较小;当流动时间大于1.37 s后,总压在轴向出现了较大的压力梯度。

3.3 试验段偏航角时空特性及其演化规律

图8(a)和(b)给出了每个截面的几何中心处在0～2 s范围内偏航角的时空特性。图8(c)给出了不同时刻每个截面的偏航角云图。图中偏航角场1为A,B,C,D,E,F截面在不同时刻的偏航角分布云图,静压场2为z=0截面不同时刻的偏航角分布云图。

图8 试验段偏航角的时空特性Fig.8 Spatiotemporal characteristics of yaw angle in test section

由图8(a)可知,流动时间在0～2 s范围内,流体在平衡阶段,其偏航角最大值为0.3°,最小值为0.1°,最大偏航角出现在试验段入口端,最小偏航角出现在试验段出口端。由图8(b)可知,试验段的流场在0.35 s和1.37 s时沿轴向的偏航角约为0.18°,角度梯度较小。从图9(c)流场的演化过程可知,在试验段流动的核心区,在建立稳定的流场后,每个截面的偏航角均小于0.5°,在流动的非核心区偏航角最大为0.7°。

图9 试验段俯仰角的时空特性Fig.9 Spatiotemporal characteristics of the pitch Angle of the test section

综上所述,根据偏航角的时空特性可知,在试验段流体流动的核心区,偏航角满足小于0.5°的设计要求。

3.4 试验段俯仰角的时空特性及其演化规律

图9(a)和(b)给出了每个截面的几何中心处在0～2 s范围内俯仰角的时空特性。图9(c)给出了不同时刻每个截面的俯仰角云图。图中俯仰角场1为A,B,C,D,E,F截面在不同时刻的俯仰角分布云图,俯仰角场2为z=0截面不同时刻的俯仰角分布云图。

由图9(a)可知,流动时间在0～2 s范围内,流体在平衡阶段,其俯仰角最大值为0.3°,最小值为0.1°,最大俯仰角出现在试验段入口端,最小俯仰角出现在试验段出口端。由图9(b)可知,试验段的流场在0.35 s和1.37 s时沿轴向的俯仰角约为0.18°,角度梯度较小。从图9(c)流场的演化过程可知,在试验段流动的核心区,在建立稳定的流场后,每个截面的俯仰角均小于0.5°,在流动的非核心区俯仰角最大为0.7°。

综上所述,由俯仰角的时空特性可知,在试验段流体流动的核心区,俯仰角满足小于0.5°的设计要求。

4 结论

本文针对悬挂发射装置空气动力学问题,采用流体力学数值模拟方法,利用试验验证算法的置信度,采用有限元体积法求解雷诺时均方程(RANS),研究了三维非定常流场的时空特性及其演化规律。主要得到以下结论:

1) 应用空气动力学知识建立了真空吸入式风洞的数学模型,得到了体积关于马赫数的数学表达式,并进行了解算。理论分析表明,当真空罐容积为2 000 m3、真空度为3 kPa时可以较好地模拟悬挂发射装置在空中挂飞和投放瞬间的气动载荷。

2) 采用计算流体力学数值模拟结果表明,真空吸入式风洞试验段流场核心区的马赫数约为0.80,且持续时间约为1 s,可以满足流场马赫数为0.40～0.80,且持续时间为500 ms的设计要求。

3) 真空吸入式风洞试验段流场的最大马赫数为0.95,不会出现激波结构,流场品质不会受到激波结构的干扰。试验段在建立稳定的流场后,流场在轴向的速度梯度和压力梯度较小,无明显变化。

4) 真空吸入式风洞试验段流场核心区的每个截面偏航角和俯仰角的最大值为0.3°,最小值为0.1°,在流动的非核心区最大为0.7°,可以满足偏航角和俯仰角小于0.5°的设计要求。

限于计算平台资源匮乏,在构建真空吸入式风洞的计算域时未考虑其双侧同步阀门的开门效应,下一步将研究基于动网格技术的双侧同步阀门开门过程的流场特性,以进一步提高真空吸入式风洞数值模拟的精度。