SAR无线电引信目标定向探测模型及仿真

张恒瑞,景 华,李楚宝,2,付胜华,牛兰杰,2,杨金钢,2

(1.西安机电信息技术研究所,陕西 西安 710065;2.机电动态控制重点实验室,陕西 西安 710065)

0 引言

引信定向探测与战斗部破片飞散角控制相结合,可实现精确控制战斗部起爆时间、弹目交会距离、方位角,使得战斗部爆炸破片指向目标,可以增加战斗部的杀伤威力[1]。激光、红外以及无线电探测引信是当前引战配合定距/定向起爆控制的主流方式[2-3],但激光、红外易受到烟雾等自然环境干扰而产生误作用。如何有效提高无线电引信定向精度,对提高引战配合毁伤具有重要意义。

合成孔径雷达(SAR)通过雷达运动形成大口径天线,从而获得具备方位向的高分辨率目标图像[1]。将SAR技术应用于无线电引信的精确目标识别与定位起爆控制,相比光学、红外引信具有全天候、全天时、抗干扰强的优点[2-3],是解决弹载高速环境下无线电引信定向起爆控制的重要技术途径。相关学者研究了机载雷达、弹载雷达导引的SAR目标成像定位追踪技术[4-7],如德国的MMW-SAR对地导弹、美国的LRASM反舰导弹等都已应用SAR技术,展现了其高精度的打击能力[8]。然而,常规弹药的雷达导引头通常存在近距盲区[9],目标的位置无法观测,因此研究SAR引信目标识别与定位技术具有现实意义。

基于SAR的定向定距探测引信的关键技术在于获取弹体与目标的方向角。文献[10—12]提出的三点线性约束自适应单脉冲测角是目前雷达中应用较广的方位角测量方法。在此基础上,文献[6]通过增加差波束副瓣约束的方法降低副瓣电平,维持线性单脉冲比斜率,提出了一种低副瓣自适应单脉冲测角方法。文献[7]通过约束条件对二维方向信息去耦合,采用广义单脉冲测角技术进行角度估计,建立了平面阵约束自适应单脉冲测角算法。但上述算法均基于机载水平面测角,对于弹载高落速大斜视落角还未开展研究。本文针对导引近距盲区弹体与目标交会段高速大斜视环境,提出了一种基于SAR的弹载无线电引信目标定向模型。

1 SAR无线电引信原理

SAR的基本原理是以小尺寸雷达的运动得到一个较长的合成孔径,进而获得与之成反比的极窄波束[13]。如图1所示,在俯冲前斜式弹目交会段,弹体无姿态变化且其偏航角、俯仰角、横滚角为0,以落角α、匀速v运动,并假设无线电引信实际的天线孔径以脉冲发射的电磁波束主瓣与弹轴的夹角(定义为主瓣前倾角)与合成孔径波束主瓣前倾角相等。

图1 无线电引信SAR原理示意图Fig.1 Schematic diagram of the radio fuse SAR principle

以线性调频(LFM)引信为例,信号时域表达式为

(1)

(2)

对应脉冲的LFM回波信号可以表示为

sn(t)=σ·ϖ(t)·s0[t-2R(t)/c],

(3)

式中:ϖ(t)为天线方向图增益。对N个脉冲回波信号进行每一步信号的求和,可以表示为

s(t)=∑nσ·ϖ(t)·p[t-nTr-2R(t)/c],

(4)

式中:ϖ(t)为天线方向图增益,R(t)为目标与引信之间的距离,Tr为脉冲间隔时间,c为光速。

通过匹配滤波器对回波信号进行脉冲压缩。设滤波器的传输函数为H(w),为了满足最大信噪比,有

H(w)=KF*e-jwt0,

(5)

式中:F*为傅里叶变换的共轭,t0是滤波器件的时间延迟,K为增益常数。则回波信号s(t)通过滤波器,经过卷积运算处理后得到的信号s1(t)表达式为

(6)

式中:δR为脉冲距离向压缩后的冲击函数。

将脉冲内的时间变化称为快时间,脉冲间的时间变化称为慢时间,其发射频率称为脉冲重复频率(PRF)。文献[14]在合成处理过程中,将每一步的回波信号按照快、慢时间重新排列为二维阵列,第n列表示第n个脉冲对应的回波,那么合成后的完整回波信号表达式可以被重写为

(7)

式中:τ=t-nTr。

2 目标定向模型设计

目标定向的关键在于获取弹体与目标的方向角。采用脉冲和差信号比幅法进行目标与弹轴交角的计算。首先,针对地面目标弹目交会的特殊环境,建立如图2所示模型。设计两束相同且相交的波束,其中,定义波束2的主瓣前倾角为θ1,波束1的主瓣前倾角为θ2,θ0为波束交点处与弹轴的夹角,其值通常为半功率波束宽度的一半,θ为合成孔径处目标与弹轴的夹角,β为实口径处目标与弹轴的夹角,即所求方位角。

图2 目标方位角计算原理示意图Fig.2 Schematic diagram of the principle of calculating the target azimuth

随后进行算法设计。定义和差波束角θk:

θ1-θ0=θ0-θ2=θk。

(9)

假设天线幅度增益方向性函数为F,可以得到两个接收天线的幅度增益方向性函数为

F1(θ)=F(θ-θ0+θk),
F2(θ)=F(θ-θ0-θk)。

(10)

令θt=θ-θ0,则波束1收到的回波信号为

u1=KF1(θ)=KF1(θt+θk),

(11)

波束2的回波信号为

u2=KF2(θ)=KF2(θt-θk),

(12)

式中,K为增益系数。得到两个波束的回波信号的幅度后,再进行比值运算,得到两个接收天线的信号幅度比为

(13)

将信号从天线的输出端加到和差变换器进行信号的求和与做差运算,得到和信号与差信号为

FΣ(θ)=F1(θ)+F2(θ),
FΔ(θ)=F1(θ)-F2(θ)。

(14)

接收的两个和波信号振幅不同而相位相同,在和差比较器的两个输入端口分别输入接收机收到的具有相同相位的目标回波信号,可以得到

EΣ=FΣ(θ)*FΣ,(θ),
EΔ=FΣ(θ)*FΔ(θ)。

(15)

对和差信号做比值:

(16)

即可以通过和差波束的输出比FΔ/FΣ算得唯一变量θ的值。

根据模型中几何关系可得

(17)

式中:d为合成天线孔径半径,R为天线中心距目标的距离,Rn为弹体距目标的距离。d与R为已知量,即可解得目标相对于弹体方位角β。

3 仿真计算及定向精度影响因素分析

3.1 回波信号仿真及测角精度验证

根据上述建立的目标定向模型可知,目标的定向精度与回波信号和差运算后的幅值,即SAR合成能力与和差波束的角度相关。初步分析可知窄波束相对有更好的幅值分辨力,即定向精度更好[15]。结合引信在实际应用中的参数进行仿真分析,不考虑弹体的姿态角,设定仿真基本参数如表1所示。

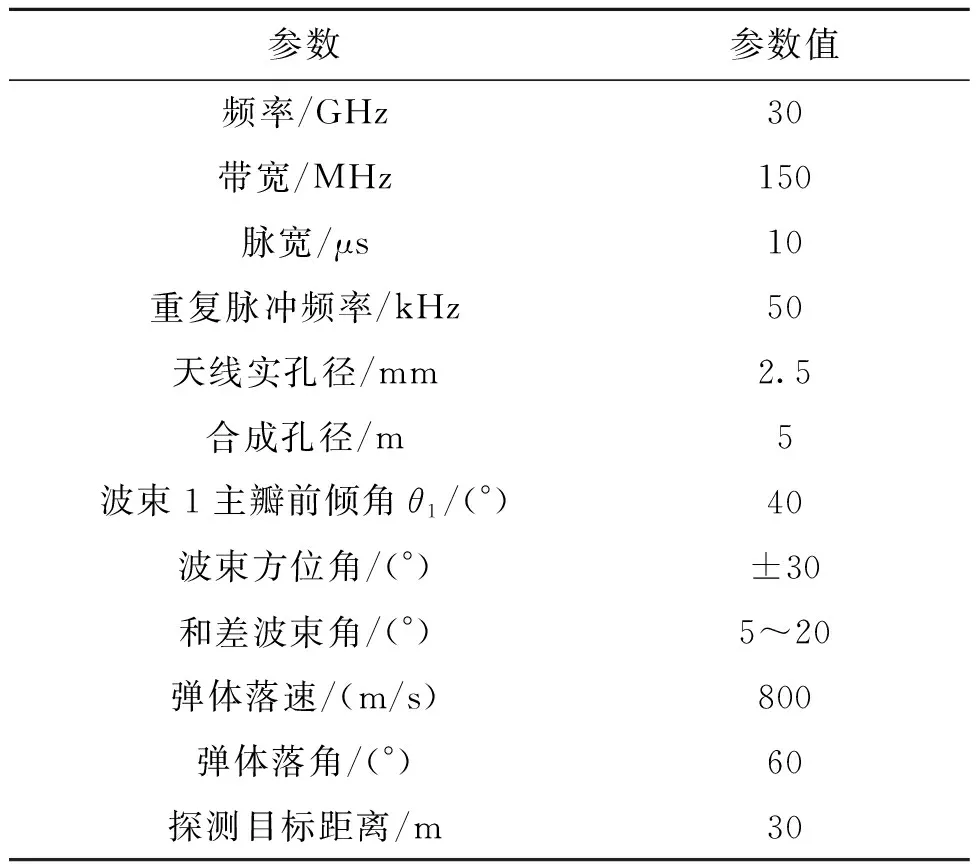
表1 仿真基本参数表Tab.1 Static rain field simulation test device

表1参数中,波束前倾角、弹体落角与落速决定了SAR的合成能力,弹体落速决定了回波信号脉冲压缩的信噪比,即方位相的分辨率[16],对此本文不做重点讨论,θ1取值为30°,弹体落角为60°,弹体落速为800 m/s。LFM信号频谱图及目标回波信号如图3、图4所示,可以看到,目标的回波信号经过SAR合成后明显提高了信噪比。

图3 LFM频谱图Fig.3 LFM spectrogram

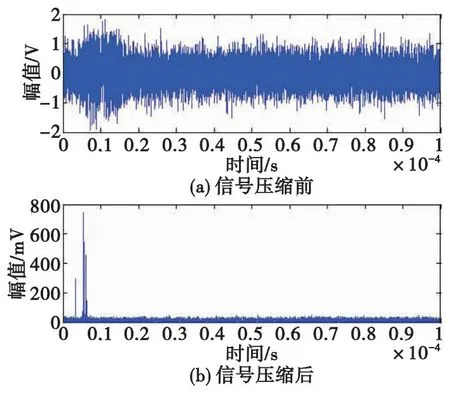
图4 LFM回波信号图Fig.4 LFM echo signal diagram

根据表1中的仿真参数,取波束2的主瓣前倾角θ2为42°,两波束的交点与主瓣相位中心的夹角θk取值为2°,得到目标在合成孔径与弹轴的夹角θ绝对值,如图5所示。

图5 方向角真值与测量值对照图Fig.5 Directional angle truth vs. measured value

可以看到测量值和真值在5°～20°有较好的拟合度,误差小于1.2°。两个夹角越小,测量精度越高。在目标距离R为30 m,合成孔径为5 m的确定参数下,通过式(17)可以得到目标与弹体实孔径的测量角度范围为39°～64°。

为了进一步验证合成孔径的优点,对不采用SAR合成的目标方向角仿真,如图6所示。

图6 未采用SAR时方向角真值与测量值对照图Fig.6 Directional angle true vs. measured plot when SAR is not used

显然在未采用SAR合成测量时,方向角测量值在接近15°时出现巨大误差,无法完成测量任务。这是因为在未采用SAR的情况下,安置的天线需要采用较大的真实孔径,从而使得两阵元的间距增大,有效测量范围降低。因此采用SAR技术能够提高测量范围和测量精度,提高适用性。

3.2 合成孔径大小对测角精度影响分析

对Ka波段实际孔径与合成孔径得到的波束方向图如图7所示。可以看到在保持发射波各项参数不变的情况下,采用SAR技术后,等效天线孔径更大,方向图收缩更明显,对目标的回波信号能量更集中,根据式(9)—式(16)的和差测角理论,可以得到的测角精度越高。

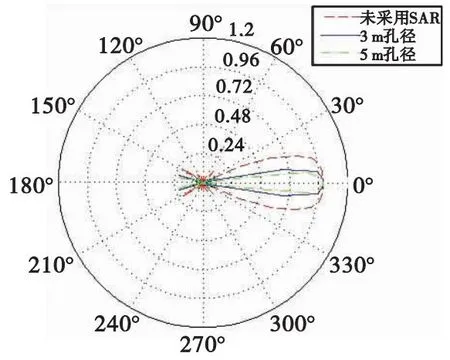
图7 不同合成孔径下波束方向图对照图Fig.7 Comparison diagram of antenna pattern under different synthetic apertures

然而,方向图的收缩带来波束扫描区域变窄,易丢失目标,对目标的方位角探测区域需要结合引战配合另作重点讨论。

3.3 和差波束角θk对定位精度影响分析

保持其余仿真参数不变,取波束1和波束2的交点与主瓣相位中心的夹角θk分别为2°,4°,6°,8°,验证测角误差结果如图8所示。

图8 不同夹角下测量误差对照图Fig.8 Comparison chart of measurement error at different angles

从图8可以看到θk越大,测角误差越大,原因是当θk增加时,两个波束相交的部分减少,所生成和差信号的适用空间减少,测量误差增大。在极端情况下,当夹角超过天线主瓣宽度,使得两个波束完全不相交时,算法工作无法完成。因此在设计天线安装时,应当控制两个天线夹角在4°～6°。

3.4 弹目交会距离影响分析

保持其余仿真参数不变,取天线中心距目标的距离R为10～30 m,验证测角误差结果如图9所示。

图9 弹目距离与测量误差关系图Fig.9 Relationship between projectile distance and measurement error

从图9可以看到弹目距离越远,测量误差值越低,原因是弹目距离越远,两个波束的回波信号区别越大,形成的和差信号越清晰,有利于提高测角精度。但在实际应用中,应当考虑战斗部起爆时对弹目距离的要求,以及考虑探测距离能力的限制。弹目距离在22～32 m时,测量角度误差值不大于3.4°。

4 结论

本文建立了一种基于SAR的脉冲测角算法。该方法基于SAR的合成原理,通过构建面向地面目标的弹目交会场景,对SAR合成回波信号进行和差计算,得到了目标与弹轴的夹角,应用于弹载俯冲的无线电引信对目标的方位角测量。验证结果显示,该算法相比未采用SAR的测角方法,能够提高测量方位的范围,在引信参数条件下,对39°～64°的目标方向识别误差不大于1.2°。算法得到了SAR合成孔径大小、目标方位角和弹目距离对定向精度的影响规律,表明了该算法的可行与泛用性,在对地引信目标定向领域具备一定的应用价值。