基于多种动力-统计方法的中国夏季降水集成预测研究
杨子寒, 托雅, 杨杰, 吴银忠, 龚志强,*, 封国林
1 苏州科技大学物理科学与技术学院, 苏州 215009
2 复旦大学大气与海洋科学系/大气科学研究院, 上海 200438
3 江苏省气象局, 江苏省气候中心, 南京 210009
4 国家气候中心气候研究开放实验室, 北京 100081
0 引言
在国家“九五”重中之重科技攻关项目“我国短期气候预测系统的研究”的支持下,我国建立了短期气候预测业务.经过气象学者几十年的努力,我国短期气候预测的理论研究及预测水平已经有了长足的发展,研制出了适用于月、季、年时间尺度的物理统计预测模型(赵振国和刘海波,2003),发展了一套适用于月、季时间尺度的动力气候模式预测系统(李维京等,2005).但是,由于大气具有复杂的非线性动力学过程,大气环流的形势常有剧烈变化或者异常情况的发生,大气运动十分不稳定,气候预测模型构建存在非线性问题处理能力的局限性,导致短期气候预测依旧面临严峻的挑战(穆穆等,2002;李建平和丑纪范,2003;王会军等,2012; Gao et al., 2023).
动力模式方法和气候统计学方法是两种经典的短期气候预测方法.但是,这两种方法自身都存在一定的缺陷,从而导致了预测技巧,尤其是针对中国夏季降水的预测也存在局限性,即单纯地使用动力方法或者单纯地使用统计方法均不能够满足当前的气候预测的需要.因此,动力和统计相结合的方法应运而生(丑纪范,1986).动力-统计方法的关键是历史相似误差的选取,即通过不同的因子及组合来选取历史相似年,进而与模式实时预测叠加以改进预测技巧.该类方法在近几年的中国汛期降水预测中发挥了重要的作用.由于影响气候异常的因子较多,而单个动力-统计预测方案只能考虑到有限数量的影响因子.与此同时,在不同的年份中,各个因子所起的作用以及起主导作用的因子均是不同的.从而导致了单个方法有时难以抓住预测年起决定性作用的相似因子(陈桂英和艾子兑秀,2000).存在某一种相似误差选取策略,在实际预测中依旧存在预测技巧年变化较大的问题.实际预测中,不同的预测方法所得到的预测结果经常出现较大的差异,这些差异也可以从不同的方面提供有用的预测信息,将其有效整合有助于进一步提升预测准确率(魏凤英,1999,2007).
目前,基于历史相似误差原理,通过从历史资料中提炼预测信息而建立的动力-统计方法已经在月-季节以及ENSO预测等短期气候预测领域开展了试验和应用,且取得了较好的初步结果(李维京等,2013).基于最优因子和异常因子两种订正方法建立的动力-统计集成的客观化预测方法在2009—2012年的汛期降水预测中,4年的预测评分(PS)为73分,体现了较高的预测技巧(封国林等,2013).Wang和Fan(2009)则以动力-统计理论为基础,发展了一种考虑历史“相似年”的空间相似预测方法.以往的研究中,也形成了一系列动力-统计预测方案,如:通过预测华北汛期降水的年际增量进行相似年选取的年增量偏差预测(范可等,2008);考虑前期关键影响因子的选取、多因子组合的优化配置构建的动态最优因子组合方案预测(杨杰等,2011;熊开国等,2012a);根据预测年前期气候因子的异常状况,构建的基于前期异常信号的误差主分量分解预测(杨杰等,2012)等预测方法.此外,模式预测误差主分量相似预测方法(Gong et al., 2016b), “大样本因子组合”的历史相似信息选取技术(Gong et al.,2018),季节降水预测中年代际尺度变化信息改进预测技术(Gong et al.,2016a)等,在东亚或中国夏季降水预测中也具有较好的应用效果.
集成预测可以有效减少预测不确定性并最大限度地综合利用各个方案,在单个预测方案的基础上进一步提高预测精度,提高综合预测结果的可靠性和准确率(刘海波等,1999).多模式集合(MME)技术在气候预测中得到了快速发展,该方法能够有效减小数值模式预测不确定性,提高预测的准确率.其主要原因在于,多个模式进行集合预测,可以减少动力模式初值条件的不确定性带来的误差,减小某些模式的预测误差,且相较于单个模式具有更高的预测技巧(吴捷等,2017).国家气候中心基于国内外多个气候模式发展了中国多模式集合预测系统(CMME),对ENSO等气候现象以及冬季和夏季的温度降水等气候要素均具有较好的预测效果(任宏利等,2018).基于复卡尔曼滤波技术的集成预测在改进我国风场、气温与降水方面也有较好效果(智协飞和黄闻,2019; 吴柏莹等,2022).因此,在现有多种动力-统计预测方法的基础上,有必要进一步开展集成预测方法研究,进而提高我国夏季降水预测准确率.
本文在分析7种动力-统计预测方法对中国夏季降水预测效果基础上,结合格点赋予动态加权,发展了动态加权动力-统计集成预测方案.在此基础上,对比分析了动态加权集成预测方法、模式系统误差订正、单个动力-统计预测方法和等权重集成预测方法对应的中国夏季降水预测空间距平相关系数和预测评分值.文章第1节阐述了本文研究所用的资料以及研究方法,基于此在第2节通过对比ACC,时间相关系数(TCC),均方根误差(RMSE)等数据比较了不同集成预测方法以及单个动力-统计方法对中国夏季降水预测的交叉检验结果.第3节给出了2021年独立样本检验效果.并在最后给出了本文的总结和简要讨论.
1 所用资料和方法介绍
1.1 所用资料
①国家气候中心全球海气耦合模式(BCC-CSM)1983—2010年6—8月的夏季集合平均的回报结果作为模式结果.②以国家气象信息中心提供的1995—2014年中国地面气候资料日值降水数据集处理为夏季降水后作为降水的实况资料.③国家气候中心整编的74项环流指数和美国国家海洋和大气管理局(NOAA)的40项气候指数共114项指数作为前期因子集.
1.2 预测区域划分
我国气候条件十分复杂,同一种动力-统计方法,对我国不同区域的预测效果差异较大,为了更好地研究各种动力-统计方法对我国的降水预测能力,将中国划分为8个区域,如图1所示.八个区分别为:(1)华南地区(110°E—120°E,20°N—25°N);(2)华东地区(110°E—123°E,25°N—35°N);(3)华北地区(110°E—123°E,35°N—42.5°N);(4)东北地区(110°E—135°E,42.5°N—55°N);(5)西北东部(90°E—110°E,35°N—43°N);(6)西北西部(75°E—90°E,35°N—48°N);(7)西藏地区(80°E—100°E,27°N—35°N);(8)西南地区(95°E—110°E,22°N—33°N)(杨杰,2013).
1.3 系统误差订正和动力-统计预测方案
1.3.1 以相似误差选取为基础的模式订正
实际大气的模拟问题可以看作是一个偏微分方程的初值问题,并且有很多学者都进行了可预测性的研究(穆穆等,2002; 吴捷等,2017).研究结果表明模拟大气的数值模式相较于实际大气总会存在预测误差(丁瑞强和李建平,2007;郑志海等,2012).因此,在模拟的数值模式中加入预测误差,以更加准确地描述实际大气的模式(任宏利和丑纪范,2005).
(1)
其中ψ(x,t)为预报量,x和t分别为空间坐标向量和时间,L(ψ)为微分算子,它对应于实际的数值模式.t0为初始时刻,ψ0为初值.t>t0时刻的ψ值可由ψ0进行积分得到或者泛函P(ψ).E为模式的误差算子,表示模式中的误差项.
从动力学角度看来实际观测资料可以理解为实际大气运动方程的一系列特解.因此,引入历史相似资料的概念,从而达到减小模式预测误差的目的.

图1 区域划分示意图


(2)
用式(1)减去式(2)可得到扰动方程:
(3)
由于式(3)中的右边为两个小项相减,其值可忽略不计,则式(3)中的上式可写成
(4)
(5)
忽略式(5)中两个小项之差,得到相似误差订正方程:
(6)
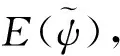
对式(6)进行积分:
(7)
由初值及历史相似可得
(8)
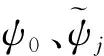
实际数值模式积分得
(9)
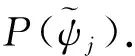
(10)

综上所述,该方程的本质是引入历史相似对应的预测误差信息来估计当前的预测误差,通过多年的实际模式预测误差资料,根据相似的初值条件寻找相应的特解,用于模式误差的预测试验(严华生等,1999).将该方法应用于国家气候中心的延伸期业务预测模式中(Bao et al.,2013;任宏利和刘颖,2013),预测效果有一定的改进,跨季节的夏季气候预测实验中也同样得到了好的结果(任宏利和丑纪范,2007).
1.3.2 几种动力-统计预测方案
结合1.3.1节中相似误差选取为基础的模式订正的原理,近些年发展了一系列动力-统计预测方案(杨杰等,2011;熊开国等,2012b).预测方案流程如图2所示.

图2 动力-统计预测方法预测流程图关键的步骤为历史相似年的选取,即历史相似误差的选取(虚线框中步骤).历史相似年选取方法不同,则对应不同的动力-统计预测方法.
本文选择了7种动力-统计预测方法与模式系统误差订正预测,共8种预测方法.主要方法原理介绍如下:
系统误差订正预测(SYS方法):计算出多年的模式预测误差的算数平均值,之后将其叠加到模式原始预测结果上得到系统误差订正预测结果.
模式原始场相似预测(EMS方法):通过模式原始预测结果,在历史上各个年份中找出与模式原始预测结果最为相似的一个年份,成为相似年,之后将相似年的预测误差叠加到模式原始预测结果上进行误差订正从而得到模式原始场相似预测结果.
误差主分量分解预测(EOF方法):首先计算出多年的模式预测误差场,对其进行EOF分解得到误差场的主分量,以预测误差场主分量的时间系数作为相似年的选取依据,以欧氏距离系数作为相似标准进行历史相似年的选取,从而最终得到误差主分量分解预测结果(熊开国等,2012b).
最优多因子动态组合方案预测(GD方法):针对不同时段,将前期因子集中的114项预测因子与汛期降水量进行相关性检验,初步筛选出相关系数通过95%信度检验的因子,之后在这些因子中进一步筛选出预测评分较高的15个因子作为该年的前期关键因子,以此得到针对不同时段的动态最优因子组合.以每个最优因子作为选取相似年的依据,将欧式距离作为相似年的选取条件,计算预测年中各个最优因子的强度与之前每年强度的欧氏距离选取相似,距离越短则越相似.每个因子选取欧式距离最短的4个相似年对应的模式误差的平均作为预报年的模式误差进行相似误差订正,共订正15次,得到最优多因子动态组合方案预测结果(熊开国等,2012a).
格点关键因子预测(GRD方法):针对不同格点,将前期因子集中的114项预测因子与汛期降水量进行相关性检验,初步筛选出相关系数通过95%信度检验的因子,之后在这些因子中进一步筛选出预测评分较高的因子作为该格点的前期关键因子.对各个前期关键因子进行单因子相似误差订正交叉检验回报评分,计算预测年中各个因子的强度与之前每年强度的欧氏距离选取相似,距离越短则越相似.选取最接近的4个相似年进行误差线性估计,以此确定预测年的相似误差.最后将各个格点订正后的结果进行合成得到全国的预测结果(杨杰,2013).
区域关键因子预测(KEY方法):与GRD方案十分类似,将区域中所包含的各个格点的数据的均值作为该区域的数据(分区如图1所示),以区域为单位进行前期关键因子筛选后,对每个区域都进行相似年的选取并以此对每个区域进行误差订正,最后将各个区域订正后的结果进行合成得到全国的预测结果.
年增量偏差预测(MAD方法):根据模式资料中各个年份相较于前一年的年降水量的数值变化,在降水实况中找出与模式资料数值的变化最接近的年份作为相似年进行相似误差订正得到年增量偏差预测结果(范可等,2008).
异常因子方案预测(YC方法):初步方法与最优因子组合预测方案相同,首先找出前期关键因子集,对前期关键因子集合进行异常检测,判断是否有因子强度发生异常(计算近27年每年前期因子发生强度的频次分布,各因子强度进行标准化处理,当因子标准化距平的绝对值大于2时,则将该因子看作异常因子),并统计异常因子的个数,根据异常因子的个数判断该预测年是否为异常年;将检测出的所有前期异常因子组合,将得到的异常因子组合进行经验正交分解(EOF),以分解出的前2个主要模态为标准进行相似年的选取,以欧氏距离系数作为相似标准进行历史相似年的选取,选取4个最相似年;将选取出的最相似年的误差场进行集合平均得到预测的误差场,然后进行订正得到异常因子方案预测结果.
综上所述,动力-统计预测方法的实质是选取与当前年份具有相似外部异常条件的历史相似年,进而计算相似年对应的历史相似误差,将相似误差与当年的模式预测结果进行叠加,达到改进模式预报技巧的效果.不同动力-统计预测方法的差异主要在于历史相似年选取的方案不同:模式原始场相似预测(EMS方法)通过模式原始预测结果选取相似年;误差主分量分解预测(EOF方法)通过预测误差场主分量的时间系数选取相似年;最优多因子动态组合方案预测(GD方法)在筛选出前期关键因子后,通过各个因子强度与之前每年强度的欧氏距离选取相似年;格点关键因子预测(GRD方法)则是针对每个格点选取历史相似年;区域关键因子预测(KEY方法)是在GRD方法的基础上,变为对每个区域选取历史相似年;年增量偏差预测(MAD方法)为根据模式资料中各个年份相较于前一年的年降水量的数值变化来选取相似年;异常因子方案预测(YC方法)在筛选出前期关键因子后,通过对每个因子进行异常检验来获得异常因子组合从而进一步选取相似年.由于不同方法选取的相似年有一定的差异,根据公式(6)计算得到相似误差订正方程存在差异,导致其与模式当前预测结果进行订正后的效果存在一定的差异.
基于上述8种方法,分别给出了各方法的2011—2021年的中国汛期降水预测结果.本文对多种动力-统计方法的结果进行集成,目的就是要集中各种方案的优势,以达到进一步改进预测效果的目的.
1.4 动力-统计集成预测方案
动态加权动力-统计集成预测方法:将7种动力-统计方法的预报结果与降水实况计算出2011—2020年的历年ACC值及ACC均值,筛选出ACC均值高于SYS且排名靠前的n(n∈[2,5])种动力-统计方法作为集成成员.用集成成员的预报结果与降水实况计算出第k名成员(k≤n)在第m年的降水距平百分率Fkm.使用类似于交叉检验的方法,将集成成员的降水预测结果与降水实况同时剔除第m(m∈[1,10])年的数据计算时间相关系数(TCC).通过公式(11)
(11)
计算出第m年每个格点上各个成员的权重wkm,其中Tkm为该格点处第k个集成成员的TCC值,wkm(k=1,2,…,n)为第k个成员在第m年该格点处的权重.由于剔除的年份不同,因此历年的集成权重是动态变化的.通过公式(12)进行集成
(12)
得到每个格点上加权集成的集成结果Om.其中Fkm为第k名成员第m年的降水距平百分率,wkm为第k名成员在该格点处第m年的权重,Om为集成出的第m(m∈[1,10])年的降水距平百分率,之后再将Om还原为降水量分布数据,得到动态加权集成结果.
等权动力-统计集成预测方法:将8种方法的预报结果与降水实况计算出2011—2020年的历年ACC值及ACC均值,筛选出预测效果较好的n(n∈[2,5])种方法作为集成成员.用集成成员的预报结果与降水实况计算出第k名成员(k≤n)在第m年的降水距平百分率Fkm,通过公式(13)
(13)
得到每个格点上等权重集成的集成结果Om.其中Fkm为第k名成员第m年的降水距平百分率,Om为集成出的第m(m∈[1,10])年的降水距平百分率,n为集成成员的数量.之后再将其还原为降水量分布,得到第m年最终的等权重集成预测结果.
汛期降水预测的主要任务之一是确定降水异常分布,降水距平百分率是重要的表征变量.本文中直接对降水距平百分率进行处理和分析,有助于提高对应的预测技巧,同时再结合气候态值计算得到降水值,则又可以分析绝对误差等改进效果.此外,用TCC值考虑权重处理时,如果直接用降水量,若集成成员在某一格点处的TCC值均为负值,各个集成成员的权重也将都为负权重,此时若直接使用预测降水进行集成,则集成预测降水量将为负值,与实际情况不符.用距平百分率则可以回避这个问题.因此,采用预测降水距平百分率进行集成,再还原出集成预测降水的处理方式.
获得集成预测结果之后,采用空间距平相关系数(ACC),均方根误差值(RMSE)和预测评分(PS)三种指标对预测结果进行客观定量化评估.
ACC是预测距平和实况距平之间的一种相关系数,反映了预测距平与实况距平空间分布上的一致程度,可以通过公式(14)进行计算:
(14)

均方根误差则表示观测值与真值之间的偏差,可通过公式(15)计算:
(15)
其中N表示预测结果的总个数,F(i)表示预测值,A(i)表示实际观测值,RMSE越小表示模式预测效果越好.
PS评分可通过公式(16)计算:
×100,
(16)
其中,N为参加评分范围内的总站数;N0,f0为距平符号预测正确的,以及预测和实况虽不同但都属于正常级(-20%<距平百分率<20%)的站数和权重系数;N1,f1和N2,f2分别为1级异常(-50%<距平百分率<-20%或20%<距平百分率<50%)和2级异常(-100%<距平百分率<-50%或50%<距平百分率<100%)预测正确的站数和权重系数;M为实况与观测均为3级异常(距平百分率<-100%或>100%)的站数.根据以往权重选择经验,为了更加关注距平程度,f0,f1,f2分别选择为2,2,4.
2 单个动力-统计预测方法的中国汛期降水预测和检验
为了初步筛选出预测效果较好的若干种动力-统计方法,分别将7种动力-统计预测方法以及系统误差订正方法共8种方法的降水预测结果,与降水实况计算出2011—2020年的ACC值(图3a)和RMSE值(图3b),并给出了时间相关系数分布图(图5).
结合图3a与表1可以发现,相较于通过模式原始预测结果进行订正的系统误差订正SYS方法,7种动力-统计预测方法的ACC均值均有较大的提高,其中,EMS,GRD,EOF,YC,KEY和GD六种订正方法将十年ACC均值从SYS的-0.08提高到了正值,具有较好改进效果,且EMS方法的预测效果最好,GRD次之.7种动力-统计预测方法的PS均值相较于SYS的65.8也具有一定的提高,其中EOF的PS均值最高,达到了69.6,EMS次之,PS均值为69.5.从图4可以看出,EMS,GRD,KEY,YC四种方法的十年RMSE值较低,具有较好的预测稳定性.结合表1与图4可以看出,EMS,GRD,EOF,KEY和YC五种动力-统计预测方法同时具有较好的预测效果与预测稳定性.

图3 7种动力-统计预测方法与模式系统误差订正给出的2011—2020年中国夏季降水预测的(a)ACC值与(b)RMSE值

表1 8种方法2011—2020年夏季降水预测的ACC均值与PS评分均值Table 1 10-year average of ACC and PS of summer precipitation in China between predictions of 8 methods and observation
图3b中,2020年份的RMSE值要普遍高于其他9个年份,为此,给出了8种方法以及BCC模式2020年RMSE值的空间分布图(图4).可以看出,8种方法以及BCC模式2020年在我国的华东地区、华南地区以及西南地区均具有较大的RMSE值,但是8种方法相对于BCC模式均具有一定改进.即使如此,由于2020年BCC模式在华东地区、华南地区的RMSE值本就较大,动力-统计方法在BCC模式的基础上进行改进,一定程度上受限于BCC模式本身的预报效果,订正后RMSE值依旧较大,故而造成集成预测后的RMSE值依旧较大.
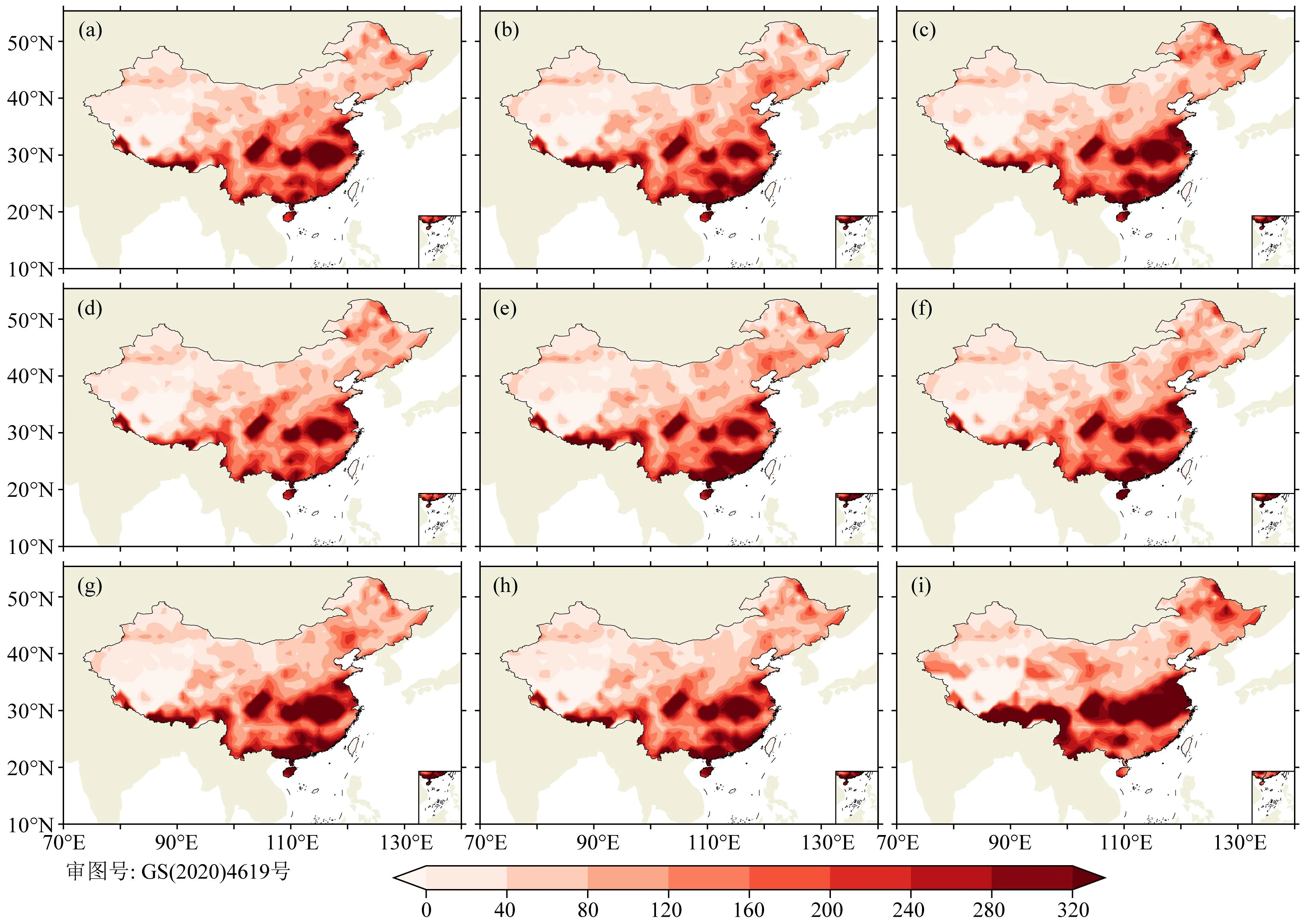
图4 8种方法与BCC模式的2020年RMSE值分布图(a) EMS方法; (b) EOF方法; (c) GD方法; (d) GRD方法; (e) KEY方法; (f) MAD方法; (g) YC方法; (h) SYS方法; (i) BCC模式.
从图5可以看出,7种动力-统计预测方法,在我国华南、华北、西南、东北以及西北等地区的预测效果均相对较好.除SYS方法以外,7种动力-统计预测方法在我国西北地区均具有较好的预测效果.华南地区则是EMS方法的预测效果最好.EMS,EOF,GRD与KEY方法在全国的大部分范围体现了较好的正相关性,均具有较好的预测效果.GD方法在我国东北地区的预测效果优于其他方法.ACC均值较高的GRD,EMS,EOF三种方法,其TCC值要明显优于其他的动力-统计预测方法,YC方法的TCC也相对较好.因此(1)动力-统计方法可在动力模式系统误差订正的基础上,进一步改进中国夏季降水预测技巧;(2)从表1可以发现,十年ACC均值较高的方法,其对应的PS评分均值也相对较高.ACC与RMSE能够较为直观的体现各个动力-统计方法相较于降水实况的预报准确率与稳定性.而PS评分则更注重于体现预测相较于降水实况的降水异常级的一致性.相较于PS评分,ACC为更为通用的选取指标.选取ACC与RMSE较好的动力-统计方法进行集成,更有利于提高集成结果的准确率与稳定性.因此,综合各个方法的预测准确性与稳定性优缺点,本文选择十年ACC均值为正值且RMSE值相对较小的EMS,GRD,EOF,YC和KEY五种方法做为集成预测成员,开展动态加权动力-统计集成预测和等权集成预测分析,以期进一步改进预测的稳定性与准确性.

图5 2011—2020年TCC空间分布图(黑点为通过95%显著性检验的站点)(a) EMS方法; (b) EOF方法; (c) GD方法; (d) GRD方法; (e) KEY方法; (f) MAD方法; (g) YC方法; (h) SYS方法.
3 中国汛期降水动力-统计集成预测和检验
基于2.1 节中国夏季降水的动力-统计单方案预测结果,结合1.4节动力-统计集成预测方案,分别选取2个,3个,4个和5个动力-统计预测方法的结果作为集成成员.本文给出8种集成预测方案:等权集成预测4种方案(A1—D1)和动态加权集成预测4种方案(A2—D2)(表2).基于不同方案,分别对2011—2020年中国夏季降水进行动力-统计集成预测.我们分别给出了各方案2011—2020年集成预测的ACC平均值与PS评分平均值(表2),历年ACC值(图6a),历年PS评分值(图6b)以及历年RMSE值(图6c).
8种集成方案中,A2方案的十年ACC均值最高,达到了0.10,相较于系统误差订正的十年ACC均值(-0.08)提升了0.18,B2方案的预测效果也较好,十年ACC均值达到了0.08,较系统误差订正提高了0.16,预测效果仅次于方案A2.效果最差的方案为方案D1,十年ACC均值为0.03,但较系统误差订正SYS的十年ACC均值依旧提高了0.11.此外,动态加权动力-统计集成预测方法2011—2020年夏季降水预测的ACC均值为0.05~0.10,较等权重集成提高了0.02~0.04,且优于绝大多数单个动力-统计预测方法的结果.动态加权动力-统计集成预测对应的ACC正值占比普遍高于等权重集成的情况,说明动态加权集成具有更好的预测效果.动态加权动力-统计集成预测PS均值达到69.3~70.7,明显优于等权重集成预测的67.8~68.5和多数单方案动力-统计预测结果.
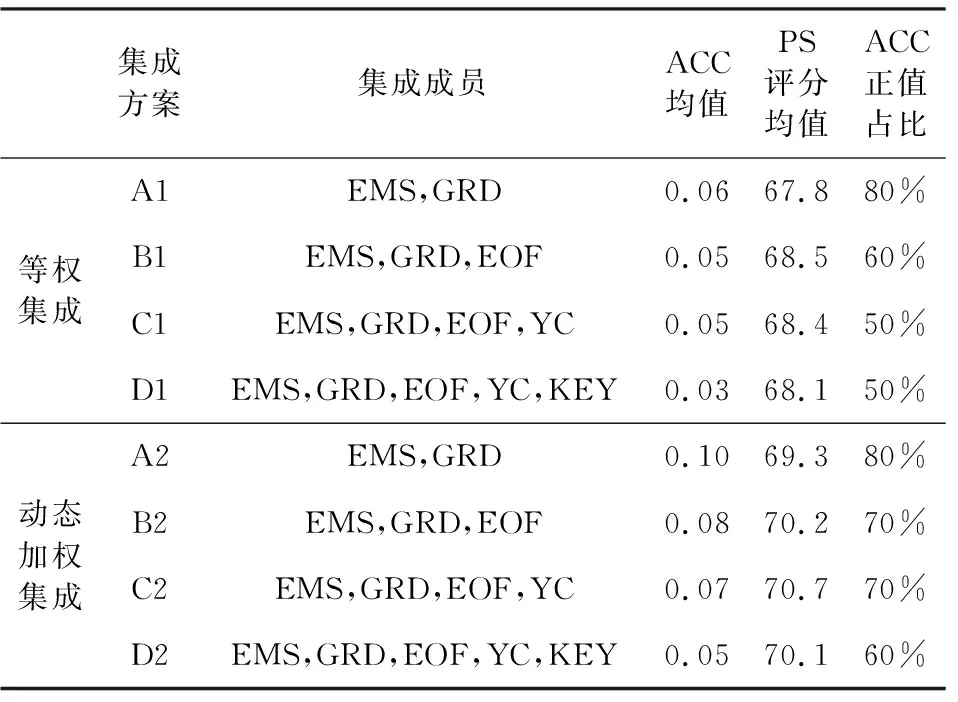
表2 8种集成方案预测中国夏季降水结果对应的2011—2020年ACC均值与PS评分均值Table 2 Average ACC and PS score of 8 integration methods from 2011 to 2020

图6 8种集成方案预测结果2011—2020年的历年(a) ACC值; (b) PS评分值; (c) RMSE值.
从图6a可以看出,集成方案对降水预测ACC整体有所提升,但部分年份如2014年并没有显著提升,甚至预测效果要低于个别动力-统计预测方案,而2020年预测效果则有较为明显的提升.集成预测的效果跟单个方案的结果有很大的关联性,单个动力-统计方法在2014年份的预测效果相对较差,且选取出的五个成员中,KEY,GRD,EOF三种方法在2014年预测的ACC值均偏低,故而造成2014年集合预测的ACC值偏低.2020年的情况则不同,选取出的五个集成成员中,EMS,GRD,EOF的ACC值本就相对较高,均为正值.因此,集成预测后,通过权重调整可适当加大正贡献的权重,降低负贡献的权重,进而改进2020年的预报效果.
从图6b可以看出,除2014和2018年外,动态加权集成预测的历年PS评分均高于等权重集成,进一步说明动态加权集成具有更好的预测技巧.
图6c为8种集成预测方案的2011—2020年的历年RMSE值.比较动态加权动力-统计集成预测对应的RMSE和等权集成预测较为接近,但较EOF,YC与KEY三种动力-统计方法的RMSE值有小幅改进.因此,动力-统计集成预测对改进ACC和PS评分效果较好,对RMSE的改进较单方案幅度较小.
图7给出了2011—2020年集成预测时间相关系数(TCC)的空间分布图.等权集成预测(方案A1—D1)中,全国大部分地区TCC为正值,且华北、华中、华南西部和西南等地区预测效果较好,TCC通过了95%的显著性检验(图7(a,c,e,g)).动态加权集成预测(方案A2—D2)中,全国TCC的空间分布特征与等权重的结果基本类似,但TCC值略有增加,通过显著性检验的站点略有增加(图7(b,d,f,h)).由此说明,动态加权集成预测其实质与等权集成预测是一致,因为两种方法均以单个动力-统计预测方法的结果为基础.此外,对比图5单个动力-统计预测方法的结果,动态加权动力-统计集成预测改进效果显而易见.

图7 2011—2020年预测的TCC空间分布图(黑点为通过95%显著性检验的站点)(a) 集成方案A1; (b) 集成方案A2; (c) 集成方案B1; (d) 集成方案B2; (e) 集成方案C1; (f) 集成方案C2; (g) 集成方案D1; (h) 集成方案D2.
为了进一步检验动态加权集成预测和等权集成预测方案的预测效果,将8种集成方案对2021年进行了独立样本检验.表3中,等权集成预测的ACC范围为0.03~0.14(PS评分为70.6~76.1),动态加权集成预测则对应0.06~0.21(PS评分为71.3~76.0).图8为2021年降水实况的距平百分率图与8种集成方案的2021年降水预测的距平百分率图.从图8可以看出,集成方案可以对东北、华中、西北地区的降水异常进行有效预测,但是对华南地区均无法进行有效的预测.这是因为等权集成预测以及动态加权集成预测均是在对单个动力-统计预测结果基础上的集成,在2021年的动力-统计订正中,相似年选取后的误差订正,虽然对全国整体的降水异常分布有较好的改进,但对华南地区的降水偏少没有能够有效改进,因此在对多种动力-统计预测结果的集成中也没有能够有效改进对华南降水偏少的预测偏差.这个问题的改进,可能需要从进一步改进动力-统计方法本身入手.

表3 8种集成方案2021年独立样本检验ACC值和PS值Table 3 ACC and PS value of independent sample validation for 8 integration methods in 2021
总体而言,无论是等权集成预测,还是动态加权集成预测,均能较好预测2021年夏季东北、华北和长江流域降水偏多,西北地区降水偏少的特征.结合表3,方案A2的预测效果最好,ACC值达到了0.21,其次是方案B2,ACC为0.17,方案D1的预测效果最差,ACC值为0.03.8种集成方案的PS评分均在70分以上,且动态加权集成的PS评分相对较高,PS评分最高达到了76分.总体来看,动态加权集成的预测效果要优于等权重集成.
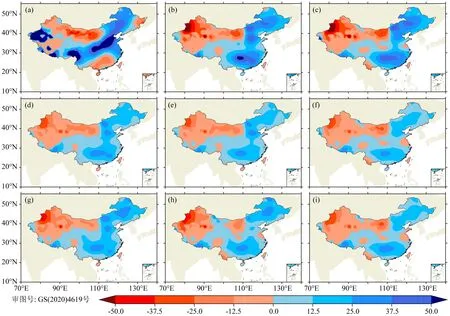
图8 2021年降水实况及预测降水距平百分率分布图(a) 2021降水实况; (b) 集成方案A1; (c) 集成方案A2; (d) 集成方案B1; (e) 集成方案B2; (f) 集成方案C1; (g) 集成方案C2; (h) 集成方案D1; (i) 集成方案D2.
综上所述:等权重集成预测的效果相较于单个动力-统计方法具有较好的改进作用.动态加权集成预测对应的历年ACC值与PS评分值均普遍优于等权重集成,表明动态加权集成预测具有更好的效果.动态加权集成预测中,并非集合成员数越多,预测效果越好,在实际的应用中需要经过更多训练和检验.
4 总结与讨论
本文选取7种动力-统计预测方法,分析比较了各动力-统计方法的预测准确性与稳定性.研究结果表明,7种动力-统计预测方法的预测准确性与稳定性相较于系统误差订正均有很大的提升,7种动力-统计方法的十年ACC均值最低为MAD方法的-0.05,而最高为EMS方法的0.10.有6种动力-统计方法(EMS,GRD,EOF,YC,KEY,GD)将十年ACC均值从系统误差订正的-0.08提高为了正值且稳定性也较好.在7种动力-统计方法中,选择十年ACC均值为正值且稳定性较好的5种方法:模式原始场相似预测(EMS),格点关键因子预测(GRD),误差主分量分解预测(EOF),异常因子方案预测(YC),区域关键因子预测(KEY方法)作为集成预测成员,发展了动态加权动力-统计集成预测方案.同时,结合不同成员数、不同集成方法,给出8种集成方案(A1—D1, A2—D2)的预测结果.研究结果表明:
集成预测效果普遍优于单个动力-统计方法的同时,也具有更好地预测稳定性.具体表现为:(1)针对2011—2020年夏季降水,系统误差订正预测方法给出的降水预测的ACC均值为-0.08,7种动力-统计预测方法给出的降水预测的ACC均值为-0.05~0.10,等权重集成预测给出的降水预测的ACC均值为0.03~0.06,动态加权集成预测给出的降水预测的ACC均值则达到了0.05~0.10,较系统误差订正提高了0.13~0.18,较等权重集成提高了0.02~0.04,且优于绝大多数的动力-统计预测方法.(2)针对2011—2020年夏季降水,四种等权重集成预测方案给出的降水预测中,ACC均值最佳达到了0.06,而四种动态加权集成预测的十年ACC均值最佳达到了0.10,且在集成成员相同时,动态加权集成的ACC正值占比要普遍高于等权重集成.(3)8种集成方案中,2011—2020年平均ACC最小值为0.03(方案D1),最大值为0.10(方案A2),较系统误差订正(-0.08)均有有显著提升,较单个动力-统计方法,也都有明显的提升.(4)8种集成方案的2021年独立样本检验中,方案A2的预测效果最好,ACC值为0.21,其次为方案B2,ACC值为0.17,动态加权集成的预测效果要普遍优于等权重集成,且8种集成方案的PS评分均高于70分.图7中各个集成预测方案的十年TCC空间分布图中有许多站点通过了95%显著性检验,可以较好预测中国主雨带位置.
就预测稳定性而言,8种集成预测方案的预测结果RMSE值要优于单个动力-统计方法,即集成预测相较于单个动力-统计方法以及系统误差订正均具有较好的稳定性.
此外,动态加权动力-统计集成预测的PS评分较等权重集成预测与单个动力-统计预测方法均有明显优势.主要表现为:动态加权集成PS评分均值为69.3~70.7,而等权重集成的PS评分均值为67.8~68.5,7种动力-统计方法的PS评分均值为66.4~69.6.在集成成员相同时,动态加权集成预测PS评分均值均优于等权重集成的结果.
综上所述,在动力-统计相结合预测的基础上,有必要进一步开展集成预测研究以提高中国夏季降水预测的准确性和稳定性.动态加权集成预测的效果要优于等权重集成预测,而集成预测最关键的步骤为如何获得各个集成成员的权重.获得权重的方法有很多,比如多峰集合的贝叶斯方法(Tebaldi et al.,2005),建立偏最小二乘回归模型(张学珍等,2017),基于深度学习建立模型(Gao et al., 2023)等.在后续的研究中,将采用不同的方法来获得权重,进一步对不同加权方法进行比较,以期进一步提高集成预测的准确性以及稳定性.
致谢感谢老师以及课题组中各位同门对本文章的帮助,感谢匿名审稿人对本文提出的宝贵意见.

