青藏高原东北缘基于W2度量的全波形成像

董兴朋, 杨顶辉, 蒙伟娟

1 中国地震局地质研究所, 北京 100029

2 清华大学数学科学系, 北京 100084

0 引言

青藏高原东北缘位于鄂尔多斯块体、秦祁地块、四川盆地及其与高原内部各块体的交汇部位(图1),是青藏高原向欧亚大陆内部扩展的前缘过渡带和印度—欧亚大陆碰撞作用由近南北向向北东和东方向转换的重要区域(Zhang et al., 2004; 刘启民等,2014).该区地质构造复杂,晚新生代构造变形显著且强震活动频繁,当前仍处于地壳增厚和岩石圈变形的初期阶段(王椿镛等,2016).因此青藏高原东北缘是研究高原横向扩展及其与周围地块相互作用机制等地球动力学问题的关键区域,同时也是理解强震孕育及发生机制的理想场所.前人已经在青藏高原东北缘开展了广泛的、多学科的地球物理研究工作.GPS观测结果表明,该区正在遭受显著的NE向的挤压(Zhang et al., 2004; Gan et al., 2007).深地震反射、宽频带地震学、大地电磁测深以及重力异常研究揭示了地壳增厚、壳内普遍存在低速高导层等特点,加深了人们对青藏高原东北缘深部构造和变形机制的认识(王椿镛等, 2003; 赵国泽等,2004; Pavlis et al., 2012; 李孟洋等,2022).

当前,青藏高原东北缘地表抬升和横向扩展机制的研究仍具有争议性.Tapponnier等(1982)认为,该区域的横向扩展主要体现为沿青藏高原内部的大型走滑断裂(如昆仑断裂、阿尔金断裂等)的东向挤出,并推测地壳与岩石圈地幔间可能存在强耦合现象.Clark和Royden(2000)基于数值模拟结果,提出高原深部地壳的弱物质因重力驱动在地质年代尺度上可发生水平向塑性流动,从而导致高原的隆升和横向扩展,且壳幔由于低黏滞中下地壳的存在而可能导致该区域壳幔解耦或至少部分解耦.随着地震层析成像和大地电磁测深研究的不断深入,证实该区域下方存在大范围壳内低波速区和高导层,地壳流模型被广泛用来解释高原的横向扩展(Clark et al., 2005).该模型为青藏高原东缘的低地形梯度以及在刚性四川盆地阻挡下,龙门山断裂带所形成的高海拔、陡峭地形提供了合理的解释.高分辨率深部结构成像是检验上述不同端元模型的基础,特别是在研究青藏高原东北缘区域中下地壳低速层的空间分布、异常幅度及其连通性等方面.

地震全波形反演理论由Tarantola于1984年提出,最初在勘探地震学领域得到应用.近年来,得益于计算机性能的显著提升和现代数值计算方法(如谱元法)的进步,实现计算区域乃至全球尺度的三维实际地球模型的理论地震图已经成为可能(Komatitsch and Tromp, 2002).不同于基于高频近似的传统射线类成像方法,全波形成像采用数值方法求解地震波方程,不仅充分考虑了实际地震波的有限频率特性,也包含了在传播过程中的散射、衍射和波前愈合等多种复杂波场效应,实现了高精度地震波形数据的有效计算.该方法同时利用地震波的相位和振幅信息约束地下结构,并涵盖射线路径之外介质对波场扰动的影响,在同等条件下其成像结果分辨率显著优于传统的射线类成像方法(Virieux and Operto, 2009).Tape等(2009)首次利用伴随成像方法,揭示了美国南加州地壳结构的显著非均质性,与初始模型相比,局部地区速度扰动可达30%;其后,Fichtner等(2009)和Zhu等(2012)应用该方法获得了澳大利亚和欧洲地区高分辨率壳幔速度结构图像.一些学者也将该方法应用到中国大陆及周边地区壳幔结构研究中,例如Chen等(2015)和Xiao等(2020)分别利用该方法获得了东亚大陆和青藏高原及其周边区域壳幔速度结构.对于区域尺度的研究,Dong等(2020)、Dong和Yang(2020)利用全波形成像方法,获得了青藏高原东北缘和华北地区高分辨率岩石圈速度结构.值得注意的是,尽管上述研究均依赖数值方法求解地震波动方程,其反演中所采用的目标函数主要还是互相关走时信息.这种处理方法(也称为拟波形成像方法,黄雪源等,2021)部分是因为走时信息与地球内部结构之间存在近似线性关系,有利于后续的稳定迭代计算;同时,由于观测数据常受到噪声的干扰和场地效应及仪器响应因素的影响,获取地震波形的绝对振幅值在实践中颇具挑战.不过,这种处理意味着可能会牺牲一定的分辨率,因为振幅信息在结构约束方面的潜力并未得到充分利用.

传统的L2度量目标函数具有很强的局限性,对数据的扰动和微小形变都会产生较大误差,原因在于基于L2范数的目标函数对数据高度非凸、存在很多局部极小值点,因此降低它的非凸性是一个长期存在的难题.在地震全波形反演研究中,这种局限性常表现为难以克服周期跳跃(cycle-skipping)问题,导致反演过程容易陷入局部极小值,降低了后续地质解释的准确性和可信度(Virieux and Operto, 2009).近年来,最优传输理论快速发展,由其引入的Wasserstein距离可以衡量两个概率分布之间的相异程度.与传统L2范数的“点对点”振幅对比不同,Wasserstein距离还考虑了观测波形和合成波形之间的相位差异,使得该度量更加精确(Villani,2003).Engquist和Froese(2014)、Yang等(2018)证明了Wasserstein度量在处理地震信号时移和振幅扰动方面表现出良好的凸性,数值算例表明采用Wasserstein距离构建目标泛函,能为全波形反演提供更加稳定且精确的目标函数,显著减少局部极小值,一致地收敛到全局最优解,提高了成像结果的可靠性.此外,该度量对地震信号中的噪声不敏感,特别适合于实际地震观测数据的波形反演.然而,Engquist和Froese(2014)、Yang等(2018)研究工作仍局限于勘探地震学领域,随后,Wu等(2018)将该度量应用于天然地震精定位研究.Dong等(2019)首次将基于二次Wasserstein度量的全波形反演方法扩展到区域尺度地震成像,并引入多窗Wasserstein距离这一新技术,进一步压制了实际地震记录中噪声对反演结果的影响,获得了川滇地区可靠的壳幔结构图像.

本文研究利用2009年1月至2022年12月期间位于青藏高原东北缘区域的114个宽频带地震台站记录到的50个区域地震事件的波形数据(图1),采用最新发展的基于W2度量的全波形成像方法,获得了该区域可靠的、高分辨率的壳幔S波速度、径向各向异性和泊松比结构.根据成像结果,重点探讨了青藏高原东北缘中下地壳流分布范围、高原与周边各块体之间相互作用机制等科学问题.

1 方法和数据

1.1 基于W2度量的地震全波形成像方法

对于单分量地震波形数据,在进行重编码和归一化处理后,可视为一维的概率密度函数,如果地震波信号的持续时间为T0,则二次Wasserstein距离定义如下(Yang et al., 2018; Dong et al., 2019)：

(1)

式中f和g分别代表合成波形和观测波形,T(t)为两个波形记录之间的最优传输映射,其表达式为：

T(t)=G-1(F(t)),

(2)

其中,G和F分别为合成波形f和观测波形g的累积分布函数：

(3)

在地震波形反演中,目标泛函的Fréchet梯度通常采用伴随状态法进行求解,即由震源激发、正向传播的地震波场与台站处激发、反向传播的伴随波场之间做互相关得到.因此,伴随震源推导和计算方法非常重要,因为它是计算目标函数梯度的前提.根据Yang等(2018)和Dong等(2019)的研究,伴随震源的数学表达式如下：

∘F(t))](t-G-1∘F(t)),

(4)

其中Γ表示非零元素为1的上三角矩阵.

1.2 基于W2度量的全波形反演处理流程

从数学上讲,全波形反演是一个带偏微分方程(PDE)约束的优化问题,其目标是通过对初始模型进行逐步修正来最小化误差函数(Tarantola,1984).首先,参考前人的研究成果(例如射线层析成像)或相关的地质先验信息,构建初始模型,并将该模型进行网格剖分,结合相应地震事件的震源机制解和震源子波函数,进行地震波场的“正传”模拟,从而生成相应的合成地震波形;其次,采用Wasserstein度量标准,对合成波形与实际观测波形进行定量对比,从而获得相应的伴随震源,并在台站处开展地震波场“反传”模拟,然后将“正传”和“反传”模拟获得的波场位移做互相关运算得到Fréchet敏感核,进而得到误差梯度;再次,利用梯度类的优化算法(如共轭梯度法等),基于计算出的误差梯度对当前模型进行更新;模型更新后,再次进行正演模拟,并与观测数据进行比对,形成一个迭代的反演循环.该循环将持续进行,直至模型理论波形与实际观测数据之间的误差降至可接受水平或满足其他预设的终止条件.

1.3 基于W2度量的青藏高原东北缘全波形成像

本研究一共50个区域地震事件参与反演,其矩震级(MW)介于4.7～6.7之间,该震级范围既能确保观测数据具备较高的信噪比,同时又避免因震级过大和破裂过程复杂而引发的点源近似失效问题.

图1 青藏高原东北缘地质构造图左上角子图展示了青藏高原东北缘在中国大陆及邻区的位置,而右上角子图为本研究中使用的地震事件及台站分布情况. ALB：阿拉善块体;OB：鄂尔多斯块体;QQB：秦祁地块;QO：秦岭造山带;SGB：松潘—甘孜地块;SCB：四川盆地; KLF：昆仑断裂;XSHF：鲜水河断裂;LMSF：龙门山断裂;LRBF：龙日坝断裂.

反演涉及4个参数：压缩波速度VP、水平极化SH波速度VSH、垂直极化SV波速度VSV及密度ρ.对于单个选定的波形窗口,基于W2度量的误差函数i表达式如下：

(5)

其中T0和T1分别代表所选定波形窗口的起始与结束时间.误差函数的变分可写成上述4个参数的Fréchet敏感核与扰动量的体积分(Zhu et al., 2015)：

+Kρδlnρ)d3x,

(6)

式中KVP,KVSV,KVSH和Kρ分别为压缩波、SV波、SH波和密度的敏感核.本研究采用谱元法程序SES3D(Fichtner, 2009)来模拟地震波的传播并进行Fréchet导数的数值计算.

本次反演的地震波频带为10～100 s,其初始模型基于FWEA18(Tao et al., 2018).波形窗口的选择通过自动选取走时窗程序FLEXWIN实现(Maggi et al., 2009),并在该目标波形窗口内计算相应的误差和伴随震源.此外,针对反演过程中地震事件和台站分布不均带来的问题,本研究采用了一种地理加权策略(Ruan et al., 2019),其核心是通过提升稀疏地震事件(或台站)分布区域的权重,并降低密集地震事件(或台站)分布区域的权重,从而更有效地平衡数据覆盖率,优化反演过程.图2展示了本研究所用地震事件和台站的权重分布情况.在反演时,所有选定波形窗口的误差函数可写成：

(7)

图2 地震事件(a)和观测台站(b)权重分布图

图3 归一化误差函数随迭代次数变化

1.4 目标模型分辨率测试

在全波形反演分辨率测试中,计算资源与评估准确性是两个必须考虑的关键因素.虽然传统的棋盘格式检测板被广泛用来评估成像质量和可靠性,但由于全波形成像所需的巨大计算量,使该方法存在困难,因为它的计算需求与实际地下结构反演相当(Zhu et al., 2012; Chen et al., 2015).与此同时,尽管Fichtner和Trampert(2011a,b)提出的点扩散函数测试方法(point-spread function test)可以评估最终模型的成像质量,该方法与目标模型分辨率之间的关系不够直观.考虑到目标函数的梯度(或称Fréchet敏感核)可以清晰地揭示模型的更新方向(Tromp et al., 2005),采用梯度的空间分布评估模型分辨率尤为合适,特别是在当前全波形成像主要基于梯度类方法迭代更新的背景下.

在研究区中心,深度为35 km的位置,设置一个0.75°×0.75°的低SV速度区,速度扰动的异常幅度为5%(图5a).结果显示,尽管SV波的Fréchet敏感核分布与速度异常区存在一定偏差,但其主要特征却得到了较好的恢复,并且VSH与VSV、VP之间的相互影响较小,表明该位置处的反演结果是可靠的(图5b—d).为进一步验证结果的可靠性,我们在上地幔85 km深度进行了额外的分辨率测试,设置参数与35 km深度相同.图6展示的测试结果证明我们的反演结果在此深度同样具有较高的可靠性.

图4 反演前后初始模型(a)与最终模型(b)的W2误差分布直方图

2 结果与讨论

图6 青藏高原东北缘模型中心深度85 km处的分辨率测试(a) 真实SV波扰动; (b) P波Fréchet敏感核; (c) SH波Fréchet敏感核; (d) SV波Fréchet敏感核. 颜色棒单位为1.0×10-18 s2·m-4.

图7 青藏高原东北缘不同深度剖面的各向同性S波速度分布子图(a)中的A-A′和B-B′代表两条垂向切片的位置.

Clark和Royden(2000)的地壳流模型指出,由青藏高原内部流出的地壳弱物质在遇到刚性的四川盆地时,在东北方向可能存在两个主要的流动路径.其一是绕过四川盆地,向东流入秦岭造山带;其二是从松潘—甘孜地块内部经昆仑断裂向北流动进入秦祁地块,并最终可能抵达阿拉善块体的南边界.然而,根据我们的成像结果,秦岭造山带在中下地壳尺度表现出明显的高S波速特征(图7b和c),这似乎表明该地区的物质黏度相对较高,与地壳流模型中所预期的低黏度状况不符.此外,Wei等(2017)基于瑞雷面波层析成像结果也揭示东秦岭下方岩石圈具有高波速特征.因此,我们认为高原内部的中下地壳弱物质并未流入秦岭造山带.

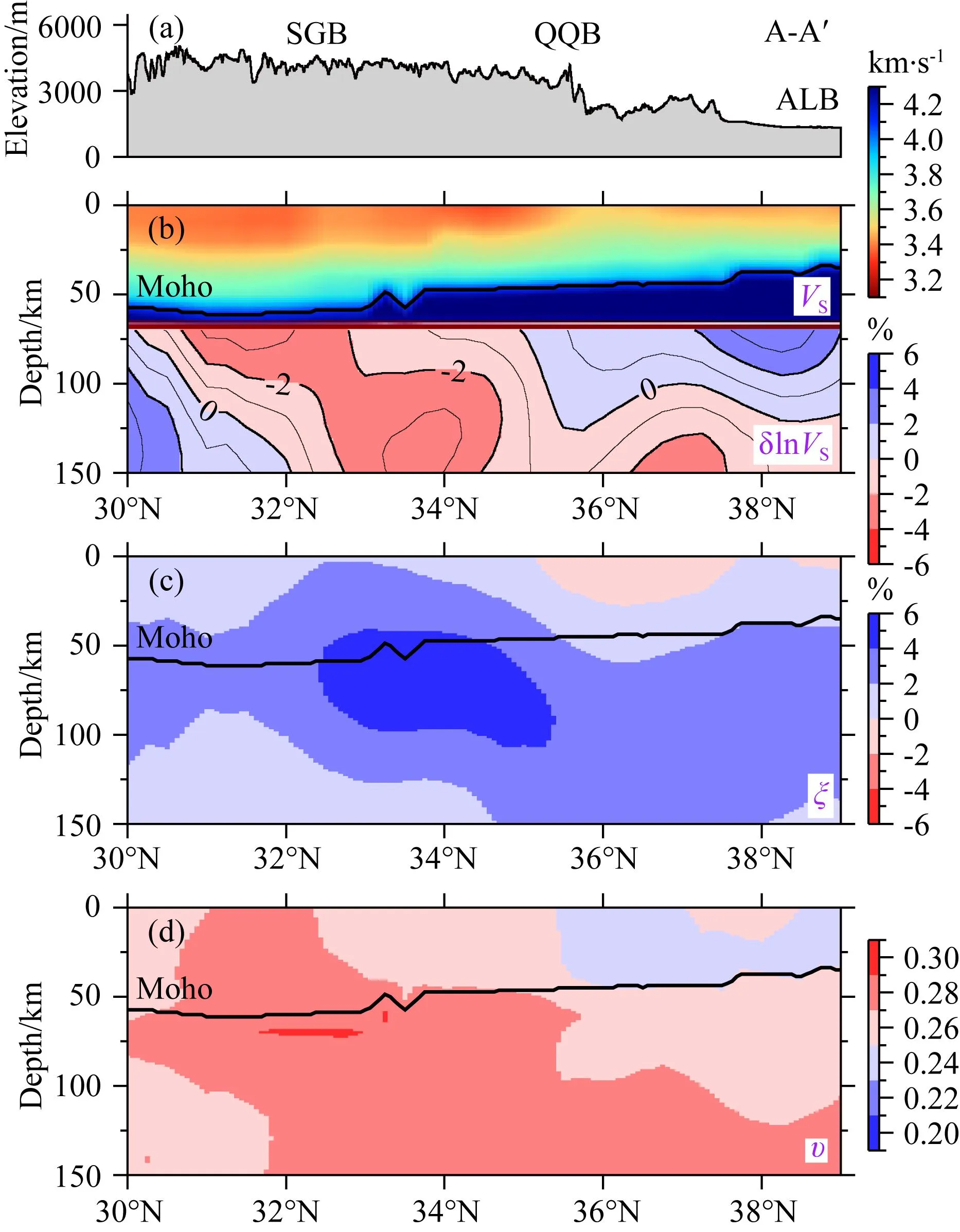
图8 沿垂向剖面A-A′的地形高程(a)、S波速度及其扰动(b)、径向各向异性(c)和泊松比分布(d)黑色曲线代表Moho面,对应模型中VS=4.1 km·s-1深度.HV：高速异常;PRA：正径向各向异性;NRA：负径向各向异性.

图8展示了沿剖面A-A′的地形高程、S波速度及其扰动、径向各向异性以及泊松比分布.基于反演得到的模型,选取VS=4.1 km·s-1作为参考波速来估算剖面下方Moho面的深度,这是地震层析成像中常用的一种估算Moho面埋深的手段.Moho面作为壳幔结构分界面,其上下两侧S波速度存在明显变化,S波在向下穿过Moho面时,其速度由约3.8 km·s-1激增到约4.4 km·s-1.因此,我们取它们之间的平均值4.1 km·s-1作为Moho的分界线.值得注意的是,不同学者选取的Moho面参考波速值可能存在细微差别(Bao et al., 2015).从松潘—甘孜块体经秦祁地块到阿拉善块体,Moho面埋深逐渐变浅,这意味着从高原延伸到外部块体时,地壳厚度逐渐减薄(刘启民等,2014).在松潘—甘孜块体,中下地壳明显表现出低S波速特征,并且伴有显著的正径向各向异性(VSH>VSV)及高泊松比异常.研究表明,岩石的泊松比会随地壳物质部分熔融程度的增加而增大(Watanabe, 1993),而中下地壳的各向异性与矿物如黑云母的晶格优势排列方向有关(Shapiro et al., 2004),这可能意味着该区域的介质强度较弱,存在部分熔融并可能在重力驱动下发生水平向运移.此特征一直延伸至秦祁地块内部,暗示地壳流可能已经跨过昆仑断裂进入秦祁地块.但在秦祁地块中部,中下地壳则呈现较高的S波速和负径向各向异性(VSH

图9 沿垂向剖面B-B′的地形高程(a)、S波速度及其扰动(b)、径向各向异性(c)和泊松比分布(d)黑色曲线代表Moho面,对应模型中VS=4.1 km·s-1深度.PRA：正径向各向异性;NRA：负径向各向异性.

图9为沿剖面B-B′的地形高程、S波速度及其扰动、径向各向异性以及泊松比分布,用于深入探讨青藏高原与四川盆地间的相互作用机制.在松潘—甘孜地块内,位于龙日坝断裂以西的区域,Moho界面埋深约为60 km.此处的中下地壳呈现出明显的低速、正径向各向异性(VSH>VSV)以及高泊松比的特征,为地壳流模型提供了有力的支持.然而,在剖面东部尤其是跨越龙日坝断裂之后,Moho界面开始明显抬升.在岩石圈尺度,青藏高原块体整体表现为明显的低速特征,代表其岩石圈强度较弱,而四川盆地则为显著的高速,反映了其作为一个刚性块体的特性.在印度板块持续推挤下,低强度的高原岩石圈与高强度的四川盆地相互作用,造成两者交界区域陡峭的地形变化(张风雪等,2018).值得注意的是,四川盆地的岩石圈基底(图9b,深度100～150 km)展现出向西延伸至龙日坝断裂附近的趋势.在径向各向异性分布上(图9c),龙日坝断裂作为一个明显的分界线,其西侧的地壳和上地幔顶部都呈现出明显的正径向各向异性,而东侧的中下地壳部分则只有弱的正径向各向异性,上地幔顶部和地壳底部的径向各向异性均为负值.这些结果表明,当地壳流从高原内部流出并越过龙日坝断裂后,其活动显著减弱.同时,龙日坝断裂东侧上地幔顶部和地壳底部以垂向变形为主,这可能是由扬子块体岩石圈基底向西楔入高原内部所致.大地电磁和剪切波分裂研究显示龙门山次级块体可能构成一个相对独立的地质单元(Zhao et al., 2012; Gao et al., 2019).在地壳尺度上,我们的成像结果与上述研究相吻合,表现为龙门山区域下方的S波速度同四川盆地和龙日坝西侧的松潘—甘孜块体存在差别.然而,需要指出的是,上述大地电磁研究的成像深度有限,主要局限在地壳尺度,而剪切波分裂研究获得的各向异性结构则缺乏深度方向上的分辨率.在岩石圈尺度上,本研究揭示高速扬子块体岩石圈基底已向西楔入高原内部并抵达龙日坝断裂附近,因此,我们认为龙日坝断裂是青藏高原和扬子块体间的一条重要的构造边界,它代表了扬子块体向高原内部延伸的最西缘(Guo et al., 2015).

3 结论

全波形成像技术为揭示地球内部结构的高分辨率特征提供了有效手段,该方法克服了传统射线类成像技术的诸多局限性(例如无限高频假设、多路径效应、分辨率等),显著提升了对复杂地质体的解析能力.然而,当采用传统的基于L2范数的目标函数进行处理时,全波形反演结果容易受到周期跳跃问题的影响,导致反演收敛到局部极小值.Wasserstein度量源于最优传输理论,它能同时考虑两个概率分布之间的相位和振幅差异,有效地克服了周期跳跃问题,从而提高了成像结果的可靠性.

本研究采用基于W2度量的全波形成像方法,利用青藏高原东北缘的密集地震台站和区域地震事件数据,获得了该区域地壳和上地幔的高分辨率结构.显著的低S波速、强正径向各向异性和高泊松比异常暗示松潘—甘孜地块中下地壳存在水平运动的弱物质流,该地壳流向北跨越昆仑断裂进入秦祁地块,并终止于秦祁地块中部.然而,在中下地壳深度,秦岭造山带却表现出显著的高速异常,这表明高原内部中下地壳流并未延伸至此.值得注意的是,龙日坝断裂两侧岩石圈存在明显的结构差异,表明扬子块体岩石圈基底已向西楔入高原内部并抵达该断裂附近.

致谢谨以此文祝贺滕吉文先生90华诞暨从事地球物理工作70年.感谢中国地震局地球物理研究所地震科学国际数据中心(http：∥www.esdc.ac.cn)提供的观测波形数据.

附录A 初始模型沿A-A′剖面的深部结构

附图1 初始模型FWEA18沿垂向剖面A-A′的地形高程(a)、S波速度及其扰动(b)、径向各向异性(c)和泊松比分布(d)黑色曲线代表Moho面,对应模型中VS=4.1 km·s-1深度.

为说明反演前后最终模型相比初始模型的提升,本研究展示了初始模型FWEA18沿剖面A-A′下方的S波速度及其扰动、径向各向异性和泊松比的分布图像(附图1),并与反演后的结果进行了详尽的对比分析(图8).相较于初始模型,反演后S波速度及其扰动图案呈现更为丰富的细节特征,Moho界面表现出更高的平滑度,其深度从高原内部向边缘逐渐抬升,这一趋势与本区域地质构造特征相吻合.最显著的提升体现在径向各向异性结果上,在初始模型中,剖面A-A′下方整体表现为大面积的正值(VSH>VSV),而反演后的模型揭示了更加精细的变形特征,特别是在秦祁地块中部地壳及上地幔顶部,观察到显著的负径向各向异性(VSH