对一道高考有关牵连速度试题教学错误的思考*

黄修斌

(南京市江宁高级中学 江苏 南京 211100)

郑永圣

(南京市江宁区教学研究室 江苏 南京 211100)

1 引言

【例题】(2013年高考上海卷第20题)如图1所示为在平静海面上,两艘拖船A、B拖着驳船C运动的示意图,A、B的速度分别沿着缆绳CA、CB方向,A、B、C不在一条直线上．由于缆绳不可伸长,因此C的速度在CA、CB方向的投影分别与A、B的速度相等,由此可知C的( )

图1 2013年高考上海卷第20题题图

A.速度大小可以介于A、B的速度大小之间

B.速度大小一定不小于A、B的速度大小

C.速度方向可能在CA和CB的夹角范围外

D.速度方向一定在CA和CB的夹角范围内

笔者听过几位教师讲解上面试题,基本是大同小异,讲解过程如下:船C沿着绳子靠向A船的同时还要绕A船转动,故将船C的速度沿着AC绳子和垂直AC绳子方向正交分解;船C沿着绳子靠向B船的同时还要绕B船转动,故将船C的速度沿着BC绳子和垂直BC绳子方向正交分解,由于绳子不可伸长,故每条船沿着绳子方向的分速度是相等的,因为是正交分解,斜边要大于直角边,所以两拖船速度一定小于C船速度,故A错误,B正确;如图2所示,C的速度方向就是在夹角ACB之外的,故C正确,D错误．故本题正确答案为B、C．

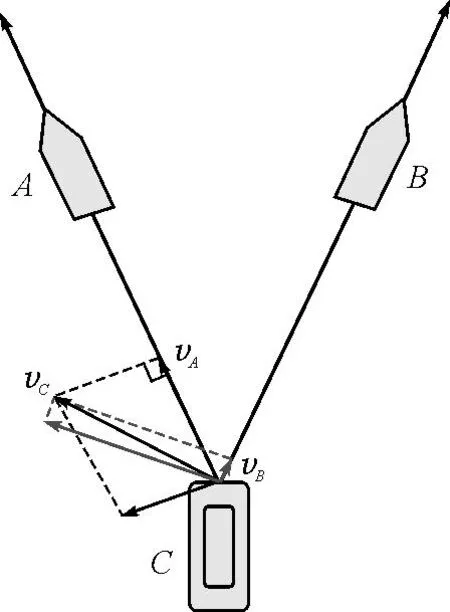
图2 船C速度分解图

显然,教师的分析是受到拉船靠岸模型的影响,如图3所示,在河岸上利用定滑轮拉绳,使小船靠岸,拉绳的速度为v,当绳与水平面成θ角时,船的速度v船是多少?

图3 拉船靠岸模型图

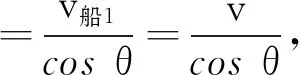
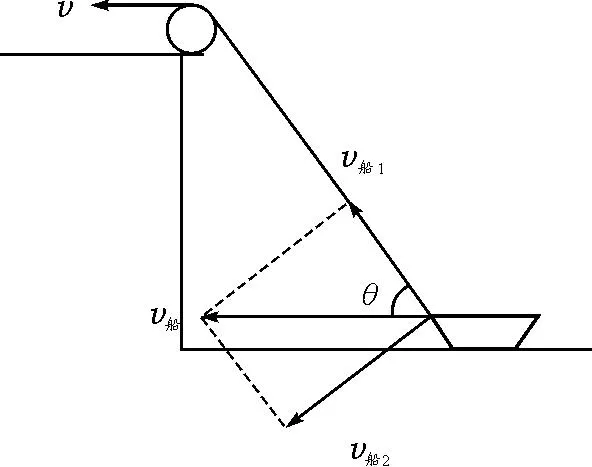
图4 船速度分解图

在讲解上面上海卷的题目时,教师没有认识到模型发生了变化,依然照搬原来的结论,从而导致出现错误．上海卷这道高考题中船C的速度既要沿着CA绳子和垂直CA绳子方向正交分解,又要沿着CB绳子和垂直CB绳子方向正交分解,且需要同时满足,那这时就不能由正交分解斜边要大于直角边得出两拖船速度一定小于C船速度了,此时必须分情形进行讨论．

2 分情形讨论

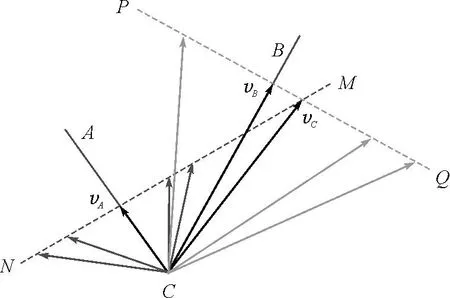
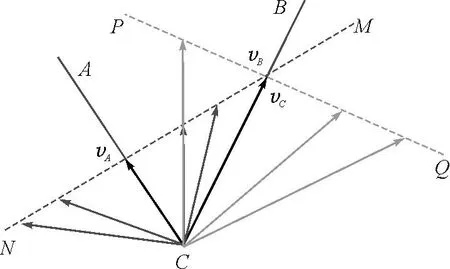
情形1：假设vA=vB．

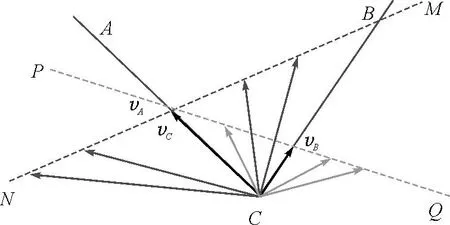
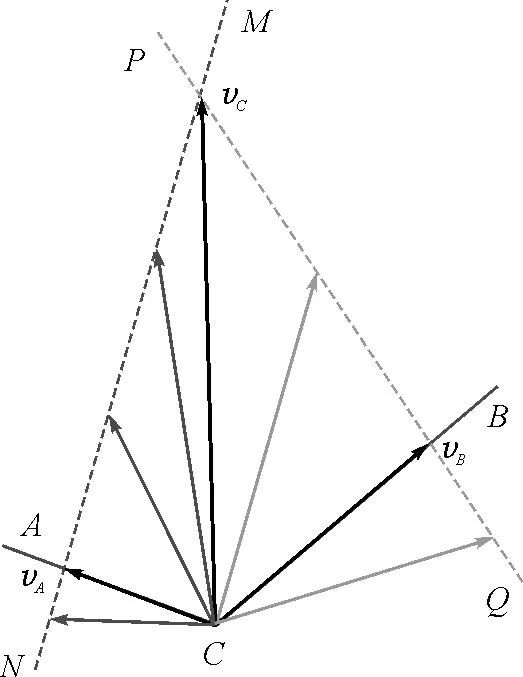
如图5所示,将船C的速度沿CA方向和垂直CA方向进行分解,所有满足条件的速度矢量为由C指向MN的虚线．同理可得,船C的速度也可沿CB方向和垂直CB方向进行分解,所有满足条件的速度矢量为由C指向PQ的虚线,如果两者同时满足的话,那么船的速度矢量vC应该由C指向MN与PQ的交点．此种情况下,vA=vB

图5 vA=vB时船C速度分解图

情形2：假设vA

第一种情况,vA远小于vB,如图6所示.

图6 vA远小于vB时船C速度分解图

由情形1同理可得,船的速度矢量vC应该由C指向MN与PQ的交点．此种情况下,vA

第二种情况,vA比vB稍小一些,如图7所示.

图7 vA比vB稍小时船C速度分解图

由情形1同理可得,船的速度矢量vC应该由C指向MN与PQ的交点．此种情况下,vA

情形3：假设vA>vB,如同情形2一样分析,也是细分两种情况进行讨论．

第一种情况,vA远大于vB,此种情况下,vB

图8 vA远大于vB时船C速度分解图

第二种情况,vA比vB略大一些,在此种情况下,vB

图9 vA比vB略大时船C速度分解图

综上所述,上题的正确答案是B、C,但教师的讲解分析过程是错误的．

当然,如果把上题中绳子CA和CB的夹角改为钝角,情况又不一样了,如图10所示,此种情况下,结论一定是船C的速度大小一定大于A、B的速度大小,且船C的速度方向也一定在CA和CB的夹角内．

图10 绳子CA和CB的夹角为钝角时船C速度分解图

3 结束语

教师讲评试题时不能仅仅是顺着答案去讲,更重要的是要引导学生学习如何去分析求解问题,不断提高学生解决问题的能力,努力培养学生的物理学科素养,为学生以后解决实际问题提供思想、方法等方面的帮助．教师在讲评试题时,知识性的错误是绝对不能犯的,必须纠正,为此教师在课前一定要多下功夫,认真备课,有些教师备新授课很认真,而对于习题课的备课有时就不太用心了,有时照着答案抄一遍就算备课了,其实这是非常不好的做法,习题课的教学教师一定要先认真研题,必须要先不看参考答案,认真独立地去先做一遍,只有这样才能对题目有深切的感受,才能知道学生在审题、解题的过程中可能在什么地方会存在困难,另外,教学中不能就题讲题,还得做适当的变式拓展,这样有利于培养学生的发散性思维．