井工煤矿全波形反演的初始模型构建探究

梁 旭，徐 裴，白喜成，李志勇，孙瑞雪，聂天文

(1.陕西小保当矿业有限公司，陕西省榆林市，719399；2.北京中矿大地地球探测工程技术有限公司，北京市海淀区，100083)

0 引言

随着煤炭开采深度的加大，地下构造变得越来越复杂，煤矿开采对煤层顶底板成像精度的要求越来越高[1]。而全波形反演技术是基于广义反演理论下对地震数据的全部波场信息的反演拟合，是一种高精度高分辨率的物探方法，对于透明工作面构建有指导作用。井工煤矿工作面的全波形反演中，良好的初始模型是关键，准确的速度场又会降低波形反演的周跳现象，从而提升全波形反演的精度。一般可以通过钻井数据建立简单层状速度模型来进行反演计算，但是在对于三维方向速度精度要求较高的运算中，就必须要对模型校准调整，从而全波形反演准确。针对此问题，前人做了大量研究，包含走时层析成像[2-3]、偏移速度分析[4-5]和不同空间域反演[6-7]等领域。石油工业上主要以走时层析成像(CT)作为全波形反演的主要初始模型来源，而在煤矿工作面勘探中，还未有相关研究的应用探究，只限于地震CT的单一应用。JACKSON M J等[8]将三维地震CT技术引入到煤层的构造探测中；SALNIKOV A S等[9]提出透射波地震数据成像方法，应用在煤矿透射勘探中；彭苏萍等[10]首次采用地震CT技术探测放顶煤工作面构造，表明成像结果可以凸显综放面内的隐伏断层；胡泽安等[11]使用2.5维地震速度层析成像方法，通过加入高程参数，消除了双巷道高程的影响，使得射线追踪的旅行路径更加准确，提升了速度反演结果。

本文主要采用三维地震CT技术的地震透射数据反演，提升“围岩-煤层-围岩”的速度模型，从而探究帮助改进全波形反演计算的方法。首先基于程函方程求解时间场[12-13]、梯度射线追踪法获得走时[14]，与实际初至走时做残差得到走时数据不适定变量，构建走时对于慢度的敏感矩阵，采用带阻尼的最小二乘反演算法[15-16]，校正三维速度场(慢度)，从而确定作为波形反演的初始大概速度轮廓，为改善全波形反演效果做辅助。

1 走时正、反演技术

1.1 正演计算

1.1.1 有限差分格式

地震波的瞬间走时可以通过程函方程计算，如式(1)所示，描述了走时梯度和地下介质慢度的关系，然后根据VIDALE J E[4]推导出的有限差分公式递推出地下网格上的每一个点的走时。

(1)

式中：t——地震走时；

x，y，z——卡尼吉亚坐标轴不同方向；

s——慢度(速度的倒数)。

为了求解式(1)，将网格上的点分成3种类型，如图1所示[4]。在图1(a)中，若已知0～6号共7个角点的走时，可以利用式(1)的有限差分形式获得式(2)，从而求解得到角点7的走时。

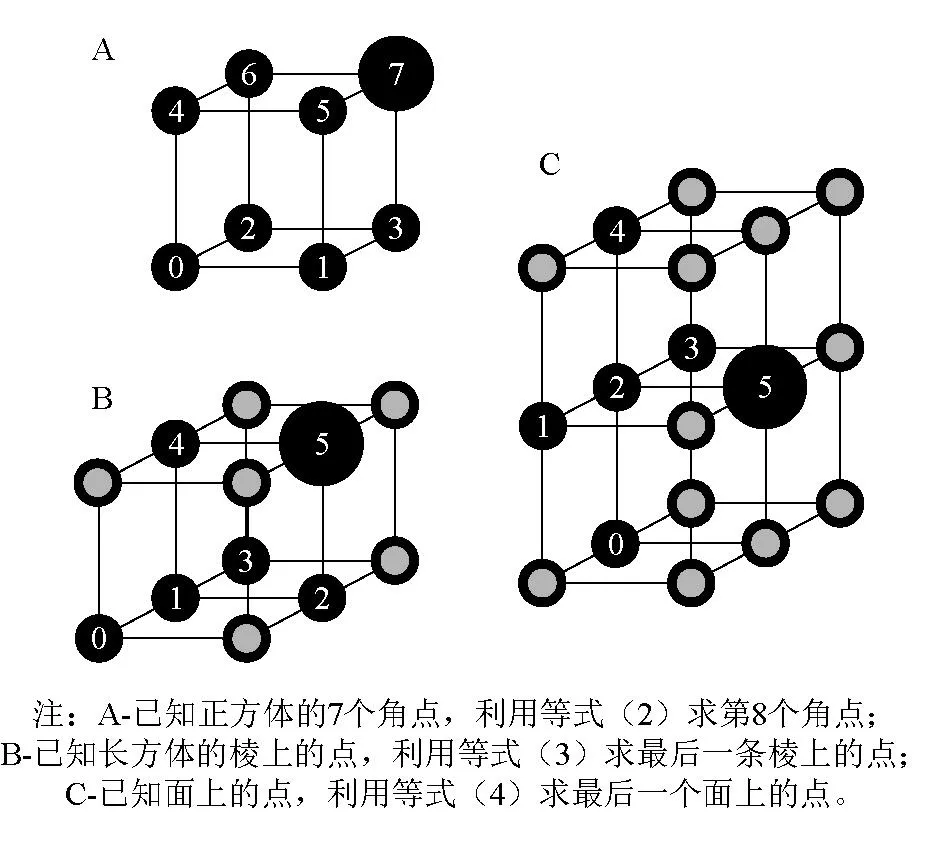
图1 计算三维均一介质的三种基本点模板

(2)

式中：h——网格间距；

ti——第i个点的走时。

图1(b)是第2种网格点类型，被用于式(2)没有计算出来的点。5号点的走时可以通过式(3)由点0～4推导得到。其中式中的慢度s是2个立方体的中心慢度值，也就是2个立方体平均慢度的平均值，而每个立方体的平均慢度是该立方体的8个角点慢度的平均值。图1(c)是第三类点，被用于计算剩余未被计算出来的网格点走时。图中5号点的走时可以通过式(4)由0～4号点计算得到。s是图中所有网格点上的慢度的平均值。

由以上式子先计算出围绕震源点的26个网格点的走时，然后按照快速行进法推进，沿波前面计算其余网格点的走时。

1.1.2 迎风格式与快速行进方法

SETHIAN J A[13]提出程函方程迎风解的快速行进法加快了计算效率。首先需要推导程函方程公式(1)的迎风格式近似于其多维度的走时场梯度值，如式(5)所示。

(5)

式中：D-、D+——正、反向算子，代表在x、y、z各方向上的导数；

sijk——网格点(i，j，k)的慢度。

简化后，式(5)可以写成以下形式：

(6)

快速行进法的核心思想是构建程函方程的迎风格式来解方程求走时场。本质上，式(6)意味着地震波信息从较小的走时传播到更大的走时。因此，快速行进法就是建立一个解方程的方案，从最小的走时向外扩散。该算法通过构建一个波前窄带让计算加快，也就是先考虑当下的波前窄带里的点，利用迎风格式去扫描，试图推进这个窄带向前，冻结当下的点，然后将新的点带入窄带结构[5]，如图2所示。

图2 迎风格式示意

这里的关键在于更新窄带结构的网格点的选择方式。具体的算法步骤如下所述。

(1)标记初始条件下的点为“可接受的值”，然后标记波前的窄带点为“近点”，最后，标记其他点为“远点”。

(2)开始循环，让在“近点”中的点取时间最小值的点作为试验点。

(3)将试验点填入到“可接受的值”群里，将之从“近点”群里移除。

(4)将所有试验点的邻点标记为“不可接受点”，如果有邻点在“远点”群中，将这个邻点从“远点”中移除，并将之添加到“近点”中。

(5)按照迎风方程(6)重新计算所有窄带邻点的时间。

(6)返回到步骤(2)。

这种算法的合理性在于重新计算迎风区的相邻点的走时无法产生比接受的点更小的值了。所以才可以向外推进走时解，总是选择最小的走时作为窄带中的网格点值，并且重新调整邻近点。

通过建立一个三维简单层状模型来测试本文正演算法，得到走时等值线，如图3所示，模型大小x×y×z=100 m×100 m×80 m，震源设置在x=50 m，y=2 m，z=2 m的位置，深度z为0～30 m地层中速度为1 800 m/s，30～80 m地层中速度为5 300 m/s。

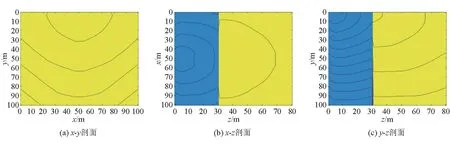
图3 简单层状结构速度模型三方向剖面及旅行时等值线

在模拟走时场时，震源作为走时起始位置，本程序中只做了简单设置为0的处理，也只做了二阶的偏微分方程求解，因此在走时传播时，存在误差，导致走时等值线有一定的抖动现象，在后续研究中，会改进算法，提升精度，本文重点对初级版本的程序做了应用探究。

1.1.3 射线追踪

在走时场t(x，y，z)中，走时场的方向余弦为l=(cosα，cosβ，cosγ)，则走时场在方向l上的方向导数式为：

(7)

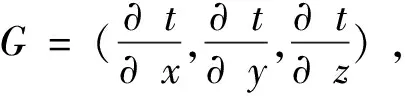
(8)

由式(8)可知，当走时场的方向向量和梯度向量的方向一致时，方向导数取最大值，与梯度的模相等，这说明走时变化率最大方向就是梯度的方向，由费马最短路径原理知，地震波传播的射线方向应该沿走时场的梯度方向变化，那么每条射线的坐标更新式如式(9)～式(11)所示。

式中：(xcurrent，ycurrent，zcurrent)——射线起始点；

(xnext，ynext，znext)——射线下一个结点；

dx，dy，dz——射线追踪的不同方向上的步长。

1.2 反演计算

使用线性最小二乘法[6]解决走时反演问题。走时和慢度之间的关系如式(12)所示，它是非线性关系，而做反演时，需要把此关系式转换为泰勒级数展开，然后通过迭代的方式求解方程。考虑一个离散的走时反演问题，此处用绝对走时。慢度模型包含离散的慢度单元，而数据包含有限个走时观测值。走时t和慢度s的关系可以表示为以下的矩阵方程：

t=Ls

(12)

式中：L——一个穿过每一个慢度单元的射线路径的长度矩阵。

由于射线路径定义矩阵L，取决于慢度s的非线性关系，式(12)的解可以通过一个初始模型开始，迭代拟合到一个正确的慢度模型和射线路径。这往往被当作一个非线性的走时反演问题。为了提升反演效率，在有限的计算空间下，采取将非线性问题线性化的方式去解决这个问题。走时和慢度的方程描述如下：

t=Fs

(13)

式中：F——非线性方程，代表走时t与慢度s的计算关系。

可以将F从初始慢度模型s0扩展开来，展开式如下：

(14)

式中：D——走时对慢度的偏导数；

δs——慢度的变化值矩阵。

忽略慢度变化值的高阶项，重组方程，可以得到：

t-Fs0≈Dδs

(15)

式(15)左边是走时剩余值，右边是一个简单的矩阵乘积项。矩阵D可以通过射线追踪后得到的有效射线长度的累计和求取获得。式(15)可以通过标准的最小二乘方法求解。对式(15)做迭代，得到慢度校正量δs，更新当前慢度模型。对模型光滑度的限制也被引入到模型校正计算过程中。一个直接的方法就是应用限制到模型光滑度上。在式(15)两侧加上Ds0，得到式(16)：

t-Fs0+Ds0≈Ds

(16)

式(16)和式(15)相同，却更容易引入反演慢度的光滑度。使用式(15)做迭代收敛到一个慢度值，使得走时剩余值r最小。将式(16)修改，包含模型的拉普拉斯差分。光滑度限制方程与走时方程相关，求解一个与走时观测值一致的光滑模型。推导之后的迭代方程如式(17)所示：

(17)

式中：si——第i次迭代的模型解；

si-1——前一次迭代的解，雅可比矩阵D可以使用si-1。

加权因子λ控制走时拟合和模型光滑的平衡，Δ是构建的慢度图像的拉普拉斯矩阵，添加一个方程系统到原始的走时反演问题中。

式(18)为慢度图像的拉普拉斯矩阵构建，相当于Sx，y，z这个中心点慢度分别离散成周边6个点的慢度值来表示，从而起到光滑图像的效果。式(19)表示下一个点距离上一个点的距离累加，从而计算随着网格行进传递的行走距离，用来表示不同射线对应的雅可比矩阵。

基于以上的公式可以构建灵敏度矩阵A：

(20)

选用最小二乘法LSQR解上述反演方程：

已知灵敏度矩阵和走时残差，得到模型校正量ds。

si=si-1+ds

(23)

式中：si——更新后的慢度模型，从而不断迭代更新速度模型。

2 合成数据测试

建立理论速度模型，如图4(a)所示。以图5作为观测系统，包括23个地面检波器，并设置3个震源，观测系统中央位置深度分别为4 500、4 100、3 800 m，它们的北方向为3 000 m，东方向为3 000 m处。图4(a)为速度模型的三维示意图，北-东方向为北-深度剖面切片向东方向的等值延展，不同颜色代表不同岩性，由不同速度值构成，其中，红色部分为4 800 m/s，深红色部分为5 500 m/s，蓝色部分为3 000、2 500、2 000 m/s(由深部到浅部依次)。用上述正演方法计算相应的初至走时。将计算的数据当作真实值，再平滑，作为初始模型，利用以上反演方法初始拟合真实数据，不断迭代，缩小拟合误差。本次实验经过20次迭代收敛到合理的误差，如图4(f)所示，反演的速度模型结果如图4(d)所示，该北视图剖面显示倾斜断层，与真实模型近似，而真实走时和计算走时拟合效果良好，如图4(e)所示。结果说明该方法可行，只是在震源处存在假异常现象，是由于观测系统局限性导致，本研究在应用时将震源异常做扣除和梯度均衡处理。

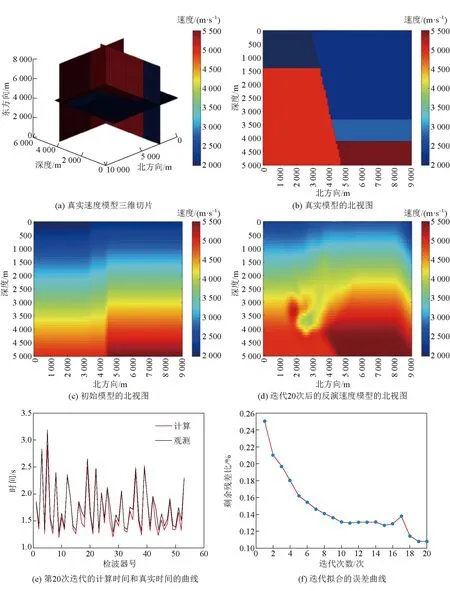
图4 复杂三维构造理论数据正反演结果

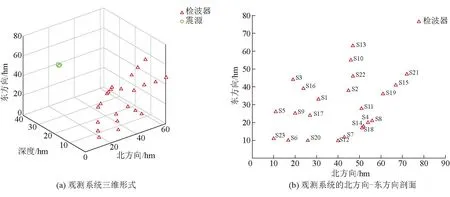
图5 理论模型观测系统

3 小保当煤矿应用案例

基于上述对透射地震数据的三维走时正反演框架，尝试引入到煤矿工作面的双巷道透射勘探中，通过拾取透射炮集的纵横波折射初至，反演拟合初至走时，从而勾勒出初始的三维速度轮廓。最终使用不同初始模型对比测试全波形反演的梯度形态来说明应用效果。

3.1 工作面概况

以小保当二号煤矿工作面132204为例，该工作面宽450 m，长1 000 m，煤层顶底板情况见表1，顶底板及围岩以砂岩和泥岩为主。地质资料显示，煤层平均厚度为2～3 m，工作面起伏较平缓，没有明显大构造揭露。

表1 煤层顶底板情况

工作面透射观测系统震源和检波器布置如图6所示，震源和检波器均大体在煤层中间层位，分别沿辅运巷和运输巷布设，检波器间距为5 m，辅运巷布设201个检波器，运输巷布设201个检波器，炮间距为10 m，辅运巷100炮，运输巷100炮。检波器为三分量采集形式，震源为炸药。

图6 相对坐标系统中的震源和检波器位置

3.2 实际地震数据的分析计算

以132204工作面的运输巷放炮辅运巷接收的第15炮三分量地震记录为例，依据其透射最短走时，估计围岩-煤层速度见表2，得到彩色走时曲线如图7所示。煤层直达波在本勘探数据中不明显，初至走时是煤层到围岩的折射波走时，所以本文主要利用折射走时反演计算，而得到围岩的横纵波速度响应，从而刻画煤层-围岩界面，提高初始模型准确度。围岩横纵波速度可以根据走时曲线拟合地震记录相位大体位置，初步估计为1 700 m/s和3 800 m/s。该工作面地震数据第15炮运输巷到辅运巷透射槽波第121道的频散谱如图8所示。由图8可知，通过比对频谱拾取点与地震记录对应相位，可以判定频散曲线的埃里相速度位置大体在923 m/s，地质资料显示本工作面属于延安2-2型煤层，与常规槽波速度范围相符[16]，其常规横波速度在1 000～1 700 m/s范围，通过三维弹性波场正演模拟计算，可以将煤层横波速度大体定为1 000 m/s，而根据所产生的槽波频谱可初步判定该组数据槽波只有勒夫型槽波一种类型，所以可以简单判定煤层的纵波速度大于围岩的横波速度，以常规纵横波比1.7为参考值，估计煤层纵波速度大体为2 200 m/s。最终设定初始速度模型参数初步见表2。

表2 初始速度模型参数

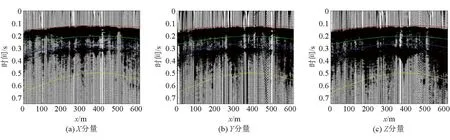
注：图中的走时曲线中，粉色表示纵波围岩折射初至，绿色表示煤层直达纵波，蓝色表示横波围岩折射到时，黄色表示煤层直达横波。

图8 实际透射数据的某一道频散谱

受透射法探测距离所限，工作面实际观测系统沿x方向分为两段0～350 m和320～1 000 m进行布设，分别建立x=350 m，y=451 m，z=28 m和x=680 m，y=451 m，z=28 m的3层模型，在深度(z)10～13 m处设置煤层，大体检波器布置到煤层中间层位，道间距为5 m，炮间距为10 m，有效炮共有192炮。按照表2为走时反演赋初值建立三层模型，利用高斯平滑将三层模型光滑，提升射线追踪效果。拾取每一炮的走时信息，如图7中粉色和蓝色走时曲线标定处，则所有走时拾取点如图9所示。将拾取横纵波的走时分别求解程函方程的反演计算系统中，纵波初至经过迭代100次，横波初至经过迭代50次，走时拟合剩余残差均方差曲线如图10所示，第15炮的合成走时和实际走时拟合情况如图11所示，得到最佳速度模型，如图12所示。

图9 纵波和横波初至拾取

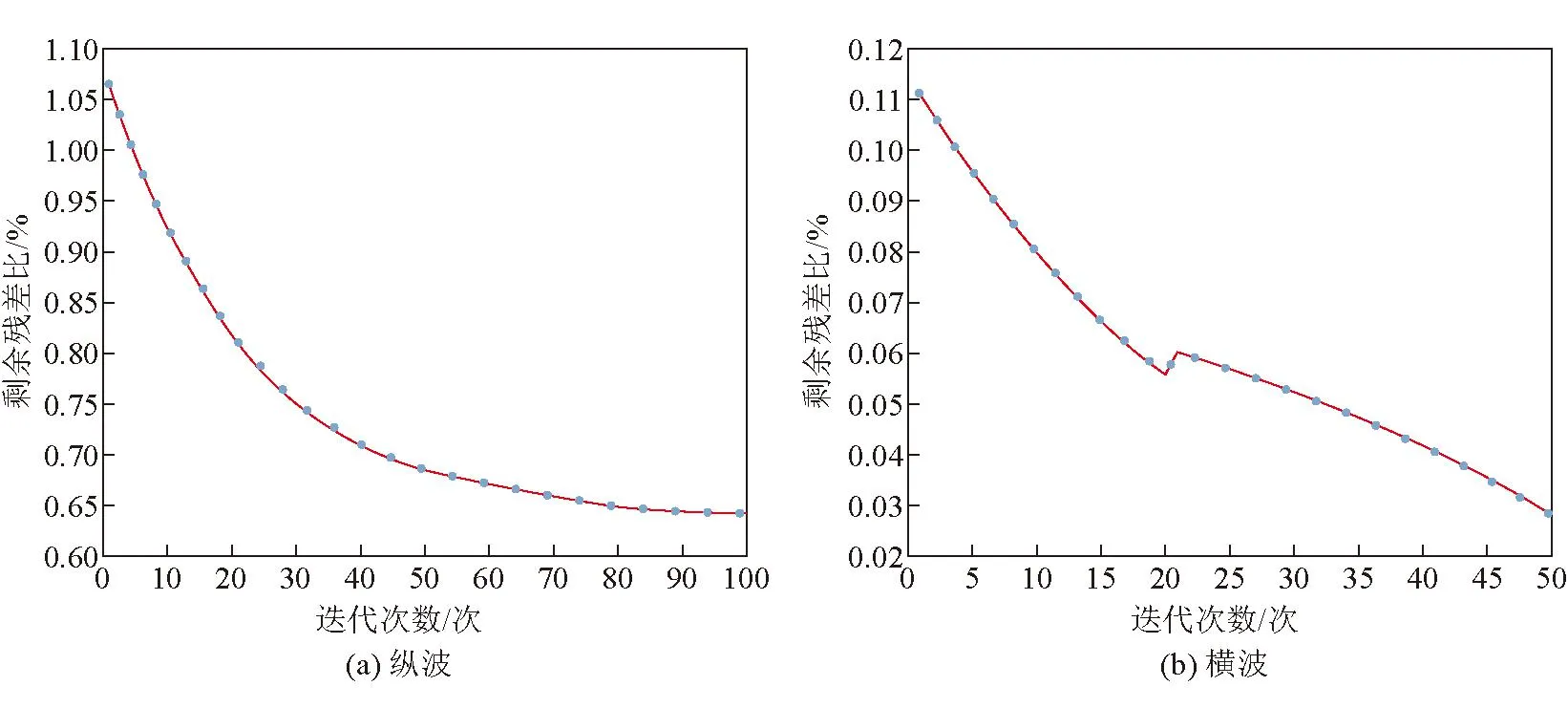
图10 走时拟合剩余残差曲线

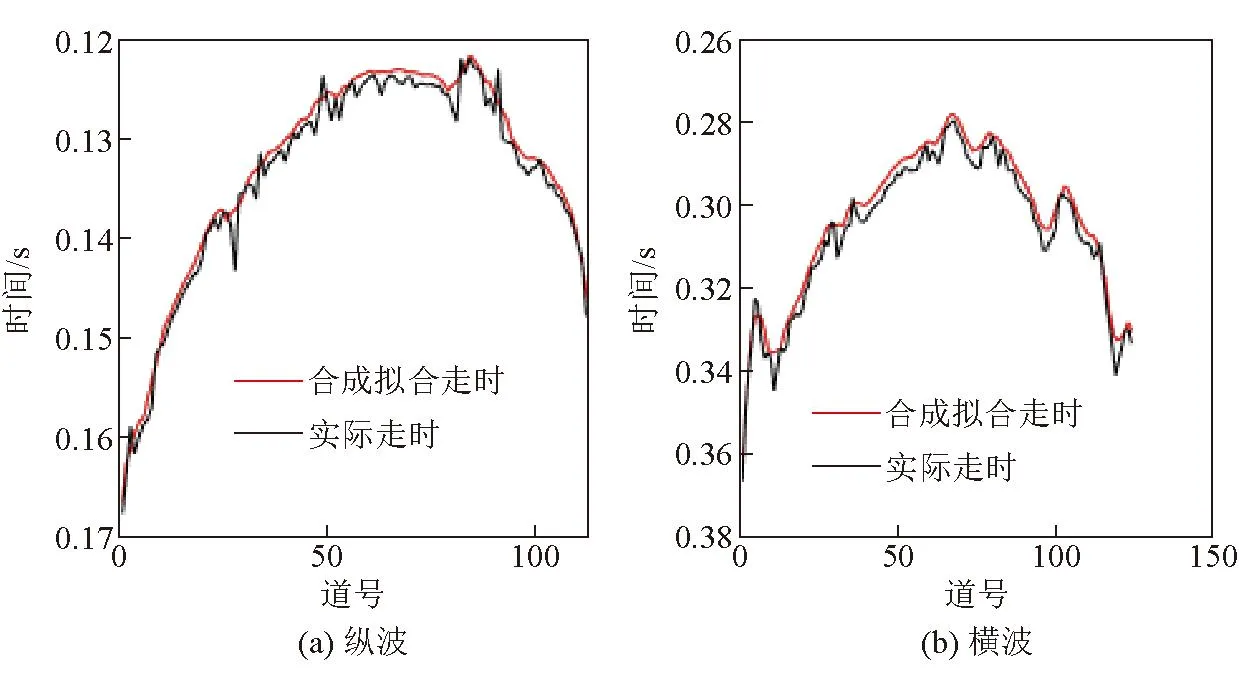
图11 第15炮单炮走时曲线(实际与合成)

图12 纵波和横波速度走时反演速度结果

将简单三层速度模型(表2)和反演得到速度模型(图12)分别输入到三维全波形反演系统中，由实际数据提取的地震子波做震源激发正演波场记录，与实际波场记录做伴随互相关得到相应模型梯度，如图13所示(在z=14 m、y=229 m、x=692 m处取切片)，比较x-y-z三方向切片，走时反演改进后的速度模型使得合成数据和实际数据的相关性更好，梯度结果趋于稳定，体现出煤层-围岩界面的连续变化，证明本方法可有效提升煤矿工作面中全波形反演效果。

图13 不同初始速度对应的全波形反演梯度

3 结论

(1)探究了对于井工煤矿工作面中三维全波形反演初始模型校正的方法，旨在缓解钻井资料建立速度模型在波形反演中的不适定性，经过三维透射走时成像大体刻画出初始速度场的轮廓，从而辅助波动反演成像的计算效果，在煤矿领域初次实践了走时CT结合波动反演的技术策略。

(2)通过结合程函方程求解时间场和反演解最小二乘目标函数的思路，初步提升三维速度场，对复杂模型的正反演理论测试验证该算法可行。

(3)实际数据结果显示，初至走时拟合而反推的速度获得的波场与简单一维层状速度模型得到的波场，分别与实际波场伴随互相关，对比其对应的梯度，前者梯度变换更连续稳定，更符合煤矿工作面的地质意义。因此，可知本研究结果可提升煤矿井下工作面中全波形反演效果的价值，可以促进煤岩分界面的刻画。